एबीबीवाई में नौकरी पाने के बारे में एक लेख पढ़ते हुए, मैं इसमें समस्या का उल्लेख करता हूं:
जल्दी - O (लॉग एन) संख्याओं पर अंकगणितीय संचालन के लिए - Nth फाइबोनैचि संख्या खोजें
मैंने इसके बारे में सोचा और महसूस किया कि ओ (एन) के दौरान काम करने वाले केवल समाधान मेरे सिर पर आते हैं। हालांकि, बाद में एक समाधान पाया गया था।
सुविधा के लिए, मैं संकेतन से आगे बढ़ूँगा

को
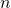
। मैं भी सेट के लिए अंकन का उपयोग करूंगा:

गैर-नकारात्मक पूर्णांक

सकारात्मक पूर्णांक हैं। तथ्य यह है कि विभिन्न गणितीय परंपराओं में, कई प्राकृतिक संख्याओं में 0. शामिल हो सकता है या नहीं हो सकता है। इसलिए, यह स्पष्ट रूप से इंगित करने के लिए अब अंतर्राष्ट्रीय गणितीय ग्रंथों में इसे पसंद किया जाता है।
तो समाधान है
नट [
१, पृ। 112 ] निम्नलिखित फॉर्म की मैट्रिक्स पहचान देता है:

पहचान प्रमाण के बिना दी जाती है, लेकिन यह काफी सरलता से साबित होती है।
दाईं ओर के मैट्रिक्स को कभी-कभी क्यू-मैट्रिक्स कहा जाता है।
निरूपित:
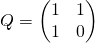
पहचान से हमें वह मिलता है

। यानी गणना करना
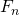
हमें मैट्रिक्स की गणना करने की आवश्यकता है
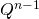
और पहली पंक्ति का पहला तत्व लें (1 से क्रमांक)।
गणना के बाद से
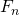
एक मैट्रिक्स को एक शक्ति बढ़ाने के लिए कम किया जाता है, फिर हम इस प्रक्रिया पर अधिक विस्तार से विचार करेंगे।
हमें कुछ मैट्रिक्स दें
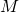
एक शक्ति के लिए उठाया जा करने के लिए
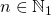
। यह भी मान लें कि
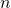
दो की शक्ति है, अर्थात्
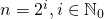
।
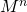
एक पेड़ के रूप में प्रतिनिधित्व किया जा सकता है:
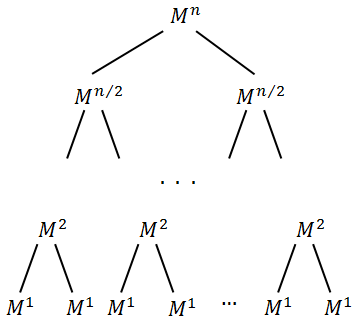
यह संदर्भित है:
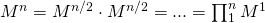
।
तदनुसार, मैट्रिक्स की गणना करने के लिए
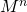
मैट्रिक्स की गणना करने की आवश्यकता है

और खुद से गुणा करें। गणना करना

आपको उसी के साथ करने की जरूरत है
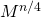
आदि
जाहिर है, पेड़ की ऊंचाई है
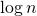
।
गणना समय का अनुमान लगाएं
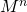
। मैट्रिक्स
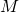
किसी भी हद तक एक निरंतर आकार है। इसलिए, किसी भी डिग्री के लिए दो मैट्रिक्स का गुणा किया जा सकता है
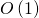
। ऐसे सभी गुणाओं को निष्पादित करने की आवश्यकता है

। इसलिए, गणना की जटिलता
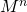
के बराबर है
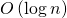
।
और अगर n दो की शक्ति नहीं है?
अब सवाल उठता है: क्या अगर
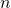
दो की शक्ति नहीं है? कोई प्राकृतिक संख्या
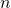
उन संख्याओं के योग के रूप में विघटित किया जा सकता है जो दो की शक्ति हैं, और दोहराव के बिना (हम हर बार जब हम किसी संख्या को द्विआधारी संख्या प्रणाली से दशमलव में अनुवाद करते हैं)। यानी

।
जहाँ

- कई डिग्री जिसके माध्यम से एक ठोस
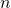
। अगर आपको वह याद है
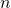
मैट्रिक्स की डिग्री है, तो हम प्राप्त करते हैं:
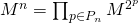
।
हालांकि सामान्य तौर पर मैट्रिक्स उत्पाद सराहनीय नहीं है, अर्थात। गुणा के दौरान ऑपरेंड का क्रम महत्वपूर्ण है, लेकिन तथाकथित के लिए क्रमपरिवर्तन की परिपक्वता का सम्मान किया जाता है। मैट्रिक्स
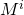
के लिए पारगम्य है
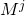
।

। इसलिए, हमें गुणा करते समय ऑपरेंड के आदेश को ध्यान में नहीं रखना पड़ता है, जिससे चीजें आसान हो जाती हैं।
तो, गणना एल्गोरिथ्म
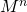
निम्नलिखित चरणों के रूप में प्रतिनिधित्व किया जा सकता है:
- विघटित
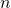 एक सेट के रूप में दो की शक्तियों का योग
एक सेट के रूप में दो की शक्तियों का योग 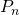 ।
। - एक सेट के सभी तत्वों की गणना करें
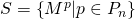 ।
। - गणना
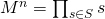 ।
।
इस एल्गोरिथ्म के चलने के समय का अनुमान लगाएं।
पहला कदम समय में किया जाता है
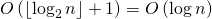
जहाँ
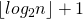
- बिट्स की संख्या में
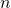
।
दूसरा चरण में किया जाता है
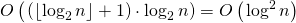
क्योंकि हमें कोई और अधिक पूरा करने की आवश्यकता है
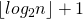
एक मैट्रिक्स को एक शक्ति में ऊपर उठाना।
तीसरा चरण में किया जाता है
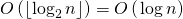
क्योंकि हमें मैट्रिक्स गुणन करने की आवश्यकता नहीं है

समय।
अनुकूलन
क्या इस एल्गोरिथ्म के चलने के समय में सुधार करना संभव है? हाँ आप कर सकते हैं। ध्यान दें कि दूसरे चरण में, सेट में मैट्रिसेस की गणना करने की विधि

। हम उनके बारे में जानते हैं कि उनमें से प्रत्येक के लिए

दो की शक्ति है। यदि आप पेड़ के साथ आंकड़े पर वापस जाते हैं, तो इसका मतलब है कि वे सभी पेड़ के कुछ स्तरों पर झूठ बोलते हैं, और बड़े लोगों की गणना करने के लिए, छोटे लोगों की गणना की जानी चाहिए। यदि हम
संस्मरण तकनीक लागू करते हैं और पेड़ के सभी स्तरों पर गणना की गई मैट्रिस को बचाते हैं, तो हम दूसरे चरण के कार्य समय को कम कर सकते हैं
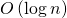
और संपूर्ण एल्गोरिथ्म का निष्पादन समय भी ऊपर है
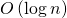
। यह वही है जो हमें समस्या की स्थिति से चाहिए।
कोड
कोडिंग पर चलते हैं। मैंने पायथन में एल्गोरिथ्म को दो कारणों से लागू किया:
- यह छद्मकोड को बदलने के लिए पर्याप्त अभिव्यंजक है;
- इसमें पारदर्शी लंबा अंकगणित है ।
यह पता चला है:
class MatrixFibonacci:
Q = [[1, 1],
[1, 0]]
def __init__(self):
self.__memo = {}
def __multiply_matrices(self, M1, M2):
"""
( 2x2)."""
a11 = M1[0][0]*M2[0][0] + M1[0][1]*M2[1][0]
a12 = M1[0][0]*M2[0][1] + M1[0][1]*M2[1][1]
a21 = M1[1][0]*M2[0][0] + M1[1][1]*M2[1][0]
a22 = M1[1][0]*M2[0][1] + M1[1][1]*M2[1][1]
r = [[a11, a12], [a21, a22]]
return r
def __get_matrix_power(self, M, p):
""" ( p )."""
if p == 1:
return M
if p in self.__memo:
return self.__memo[p]
K = self.__get_matrix_power(M, int(p/2))
R = self.__multiply_matrices(K, K)
self.__memo[p] = R
return R
def get_number(self, n):
""" n-
( n )."""
if n == 0:
return 0
if n == 1:
return 1
powers = [int(pow(2, b))
for (b, d) in enumerate(reversed(bin(n-1)[2:])) if d == '1']
matrices = [self.__get_matrix_power(MatrixFibonacci.Q, p)
for p in powers]
while len(matrices) > 1:
M1 = matrices.pop()
M2 = matrices.pop()
R = self.__multiply_matrices(M1, M2)
matrices.append(R)
return matrices[0][0][0]
mfib = MatrixFibonacci()
for n in range(0, 128):
num = mfib.get_number(n)
print(num)
,

. :
def get_number(self, n):
if n == 0:
return 0
a = 0
b = 1
c = 1
for i in range(n-1):
c = a + b
a = b
b = c
return c
.

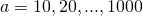
.

MatrixFibonacci IterationFibonacci (, ). 10 000

.
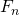
. :
n <tab> T1 <tab> T2. .
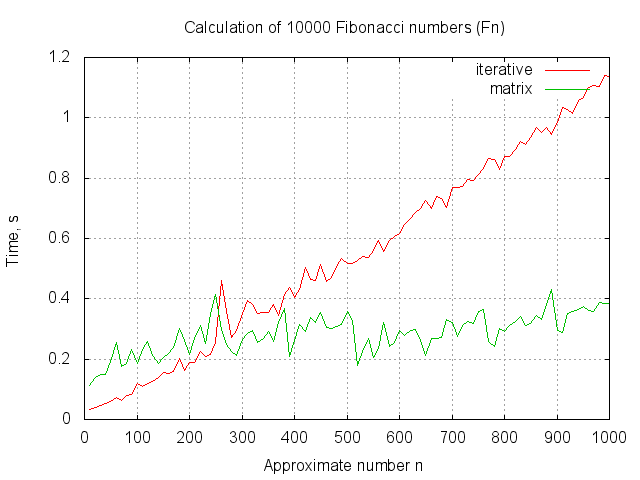
, -
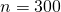
(c ,

64 ). , , .
. gnuplot —
.
P.S. , TeX- . , .
- . , 1. . — 3- . — .: «», 2006.