🏁 🔥 🖐🏻 फास्ट मोडुलो इंडेक्स गुणा 🧒 🛢️ ⭕️

परिचय

आमतौर पर इस सामग्री को सूत्रों की एक बहुतायत के साथ प्रदान किया जाता है और गणितज्ञों के लिए अधिक डिज़ाइन किया जाता है। मैं इस पद्धति को हार्डवेयर स्तर पर माइक्रोइलेक्ट्रॉनिक में लागू करने के दृष्टिकोण से सरल संख्यात्मक उदाहरणों के साथ सबसे अधिक सुलभ पेंट करने की कोशिश करूंगा। संख्यात्मक उदाहरणों में, p = 11 का उपयोग स्पष्टता के लिए किया जाएगा।

समस्या का बयान

मान लीजिए कि हमें निम्नलिखित फ़ॉर्म का गुणा करने की आवश्यकता है: res = (a*b) mod p , जहाँ
0 <= a < p
0 <= b < p
p एक अभाज्य संख्या है।
mod p - शेष modulo खोजने का संचालन।
और इसे निम्न स्तर पर किया जाना चाहिए, जहां कोई गुणन ऑपरेशन नहीं है और शेष भाग को लेने का संचालन है, या उन्हें काफी मुश्किल से लागू किया जाता है (उदाहरण के लिए, इलेक्ट्रॉनिक डिवाइस में)।

सबसे सरल उपाय विधियाँ

पहली बात जो मन में आती है: गुणा करें, फिर विभाजित करें और शेष लें। इस दृष्टिकोण को अस्तित्व का अधिकार है, लेकिन संचालन की संख्या के मामले में बेहद महंगा है और इसे लागू करने में काफी मुश्किल है।
दूसरी बात जो आप सोच सकते हैं, वह है कि इस ऑपरेशन को दो-आयामी गुणन तालिका के आकार p साथ लागू करें। जो समझ में आता है कि यदि p छोटा है, लेकिन जैसे-जैसे पी बढ़ता है, तालिका के चतुर्भुज को बढ़ाने की लागत बढ़ जाती है (छवि 1)।

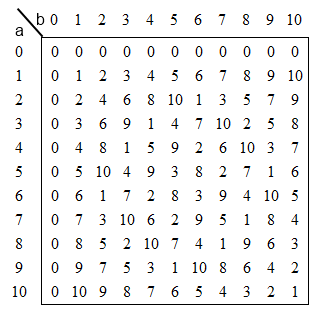चित्रा 1. पी = 11 के लिए गुणा तालिका मोडुलो पी।

सूचकांक विधि गुणक

हालांकि, एक ऐसी विधि है जिसमें आयाम p एक (या दो की सुविधा के लिए) की आवश्यकता होती है। विधि इसके अलावा गुणा के प्रतिस्थापन पर आधारित है। और निम्न चित्र (छवि 2) द्वारा योजनाबद्ध रूप से चित्रित किया जा सकता है:

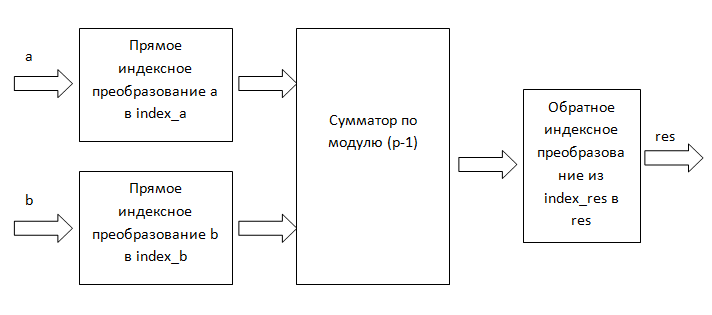चित्रा 2. सूचकांक गुणा।

आइए हम बताते हैं कि ऐसा क्यों संभव है। संख्या का सूचकांक प्रतिनिधित्व प्रतिपक्षी मूल मोडुलो p [1] की अवधारणा पर आधारित है। W की आदिम जड़ एक पूर्णांक है जिसकी शक्ति 0, 1, 2, …, (p-2) बढ़ाती है 0, 1, 2, …, (p-2) जो गैर-दोहराता हुआ अवशेष modulo p । एक आदिम जड़ हमेशा किसी भी प्राइम p (1801 में गॉस द्वारा साबित) के लिए मौजूद है। इस स्थिति में, अंतराल (0; p) से प्रत्येक पूर्णांक संख्या एक संख्या के साथ जुड़ी हो सकती है जैसे कि q = (w ⁱ ) mod p । और इस प्रकार निम्नलिखित पत्राचार प्राप्त करें:
(a*b) mod p <-> w^((ia+ib) mod (p-1)) [2]।

मॉड्यूल p = 11 लिए एक उदाहरण पर विचार करें। इस मापांक मान के लिए मूल जड़ w है। 2. यह सत्यापित करना आसान है कि 0, 1, ... 9 की शक्ति के लिए w को बढ़ाते हुए: अद्वितीय परिणाम हैं:

(२ ^० ) mod ११ = १ mod ११ = १
(२ ^१ ) mod ११ = २ mod ११ = २
(२ ^२ ) mod ११ = ४ mod ११ = ४
(२ ^३ ) mod ११ = 11 mod ११ = 11
(२ ^४ ) mod ११ = १६ mod ११ = ५
(२ ^५ ) mod ११ = ३२ mod ११ = १०
(२ ^६ ) mod ११ = ६४ mod ११ = ९
(२।) mod ११ = १२) mod ११ = 11
(२।) mod ११ = २५६ mod ११ = ३
(२ ^९ ) mod ११ = ५१२ mod ११ = ६

नियमित {q} और इंडेक्स {i} अभ्यावेदन के बीच रूपांतरण तालिका प्राप्त करने के लिए, आरोही क्रम में मूल्यों के परिणामस्वरूप जोड़े को सॉर्ट करना आवश्यक है। इस प्रकार, मॉड्यूल p = 11 के लिए प्रत्यक्ष रूपांतरण तालिका इस तरह दिखाई देगी:

क्ष	1	2	3	4	5	6	7	8	9	10
मैं	0	1	8	2	4	9	7	3	6	5

और p = 11 मॉड्यूल के लिए उलटा रूपांतरण तालिका इस तरह दिखाई देगी:

मैं	0	1	2	3	4	5	6	7	8	9
क्ष	1	2	4	8	5	10	9	7	3	6

अभिव्यक्ति का मान ज्ञात करें (3 * 5) mod 11. संख्या 3 और 5 में संबंधित सूचकांक 8 और 4 हैं (तालिका 1 देखें)। इन सूचकांकों modulo (11-1) = 10 को सारांशित करने पर हमें परिणाम मिलता है (8 + 4) mod 10 = 12 mod 10 = 2. तालिका 2 से हम पाते हैं कि अनुक्रमणिका 2 के लिए व्युत्क्रम परिवर्तन 4 का अंतिम परिणाम देता है।

सूचकांक गुणक के संरचनात्मक आरेख एम = 11 पर विचार किए गए उदाहरण के लिए निम्न आकृति (छवि 3:) में देखा जा सकता है।

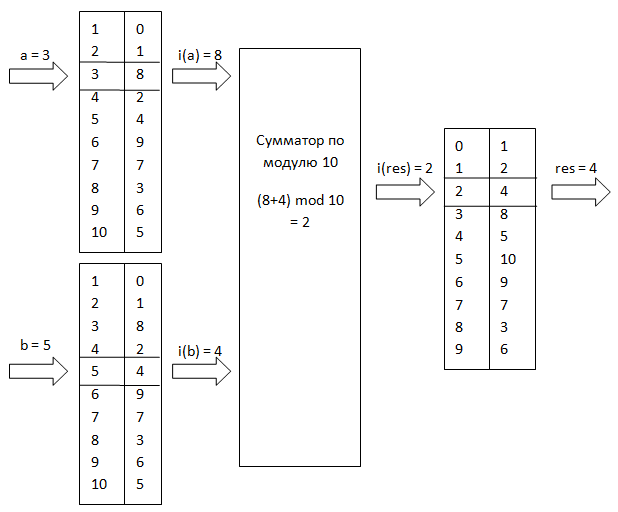चित्रा 3. पी = 11 के लिए सूचकांक गुणक की योजना।

इनपुट्स के लिए शून्य मान

यदि आप तालिकाओं को करीब से देखते हैं, तो आप देख सकते हैं कि इनपुट डेटा के लिए कोई शून्य मान नहीं हैं। यह इस तथ्य के कारण है कि ^{i का} कोई मान नहीं है! इस मामले को अलग से संसाधित किया जाता है (या इसके प्रसंस्करण के लिए विशेष नियमों के साथ एक विलक्षणता की अवधारणा पेश की जाती है)। यदि गुणक के किसी एक इनपुट पर 0 दिखाई देता है, तो आउटपुट में 0 भी होगा, जो सीधे गुणन के नियमों का पालन करता है।

गुणक का समानांतरकरण

यह पता चला है कि गुणा भी तेजी से किया जा सकता है। यदि संख्या (p-1) को पारस्परिक रूप से सरल कारकों p-1 = m1*m2*…*mr में विभाजित किया जा सकता है, तो इसके अलावा ऑपरेशन को छोटे आयामों के r अलावा संचालन में विभाजित किया जा सकता है। इस मामले में, सूचकांक निम्न सूत्र के अनुसार, लंबाई r एक वेक्टर में बदल जाता है: ( i mod m1, i mod m2, …, i mod mr )। और सदिश वेक्टर के प्रत्येक तत्व के लिए स्वतंत्र रूप से किया जाता है।

इसे एक उदाहरण के रूप में देखें। p = 11 के लिए, p -1 = 10 का मूल्य और इसे पारस्परिक रूप से सरल कारकों में विभाजित किया जा सकता है: 10 = 2 * 5 ( m1 = 2, m2 2 = 5)। इस मामले में, तालिका 1 को इस प्रकार लिखा जा सकता है:

क्ष	1	2	3	4	5	6	7	8	9	10
मैं	0	1	8	2	4	9	7	3	6	5
(I `mod` 2, i `mod` 5)	(0, 0)	(1, 1)	(0, 3)	(0, 2)	(0, 4)	(1, 4)	(1, 2)	(1, 3)	(0, 1)	(1, 0)

उलटा परिवर्तन की एक तालिका, क्रमशः, इस प्रकार है:

(I `mod` 2, i `mod` 5)	(0, 0)	(0, 1)	(0, 2)	(0, 3)	(0, 4)	(1, 0)	(1, 1)	(1, 2)	(1, 3)	(1, 4)
क्ष	1	9	4	3	5	10	2	7	8	6

हम पिछले उदाहरण के अनुसार, मान (3 * 5) mod 11. पहले हम तालिका में संबंधित वैक्टर के लिए देखते हैं: 3 -> (0, 3), 5 -> (0, 4)। फिर हम तत्व से तत्व जोड़ते हैं ((0 + 0) mod 2, (3 + 4) mod 5) = (0, 2)। व्युत्क्रम परिवर्तन की तालिका से हमें उत्तर मिलता है: (0, 2) -> 4. समानांतर गुणक योजना नीचे दी गई है (चित्र 4)।

चित्रा 4. पी = 11 के लिए एक समानांतर सूचकांक गुणक की योजना।

एक आदिम जड़ की तलाश कैसे करें?

सच कहूं, तो मैंने यह सवाल नहीं पूछा। मैं 2 से पी से शुरू होने वाली संपूर्ण खोज का उपयोग करता हूं। या आप तैयार किए गए अनुक्रम का उपयोग कर सकते हैं: oeis.org/A046145 । यदि अधिक कुशल विधि है, तो टिप्पणियों में लिखें।

योजक मॉडुलो (पी -1) कैसे डिज़ाइन करें?

योजक मॉडुलो (p-1) के इनपुट डेटा की ख़ासियत के कारण, अर्थात् दोनों इनपुट p-1 से कम संख्या प्राप्त करते हैं, जिसका अर्थ है कि उनकी राशि 2*(p-1) से कम है। इस से यह इस प्रकार है कि आप किसी भी मानक योजक का उपयोग कर सकते हैं, जिसका आउटपुट निम्न एल्गोरिथम के अनुसार समायोजित किया जाता है: यदि मान (p-1) से अधिक या बराबर है, तो परिणाम से घटाएँ (p-1) , अन्यथा अपरिवर्तित छोड़ दें।

वेरिलोग जेनरेटर

अपने खाली समय में, मैंने मॉडुलो इंडेक्स गुणक को लागू करने के लिए वेरिलोग के ऑनलाइन जनरेटर को लिखा। वहां, उनके काम का एक रेखाचित्र तैयार किया गया है।
गुणन मोडुलो 11 के लिए वेरिलोग
मॉडुलो 31 के लिए वेरिलोग
1000 तक की मनमानी संख्या के लिए वेरिलोग जनरेटर

साहित्य

[१] en.wikipedia.org/wiki/%D0%9F%D0%B5%D1%80%D0%B2%D0%BE%D0%BE%D0%BE%D0%B1%D1%D1%D0%B0%D0%E B7% D0% BD1 D1% 8B% D0% B9_% D0% BA% D0% BE% D1% 80% D0% B5% D0% BD% D1% 8C_% 28% 1% 82% D0% B5% D5% BE% D1% 80% D0% B8% D1% 8F_% D1% 87% D0% B8% D1% 81% D0% B5% D0% BB% 29
[२] www.researchgate.net/publication/224735018_A_fast_RNS_Galois_field_multiplier

लेखक से

यदि आपके पास लेख के अतिरिक्त हैं, तो मुझे टिप्पणियों में उन्हें देखकर खुशी होगी। और फिर भी लेख विवरण के साथ लिंक पर खराब निकला, अगर किसी के पास फेंकने के लिए कुछ है। =)

फास्ट मोडुलो इंडेक्स गुणा