🥘 👨🏿‍🤝‍👨🏽 🤵 .NET में गणितीय अभिव्यक्तियाँ (पार्सिंग, विभेदन, सरलीकरण, अंश, संकलन) 🙆🏿 🐒 👶🏿

स्कूल के समय से, मैं विश्लेषणात्मक व्युत्पन्न और अभिव्यक्ति को सरल बनाने के लिए एल्गोरिथ्म में दिलचस्पी ले रहा था। यह कार्य बाद में विश्वविद्यालय में प्रासंगिक था। यह तब था जब मैंने इसे लागू किया था, लेकिन यह मेरे इच्छित तरीके से काम नहीं कर रहा था: आईएल कोड के बजाय, मैंने सिर्फ टेक्स्ट फॉर्म में सी # कोड उत्पन्न किया, विधानसभाओं को अनलोड नहीं किया गया था, और इसके अलावा, विश्लेषणात्मक रूप में डेरिवेटिव प्राप्त करने का कोई तरीका नहीं था। लेकिन तब मैं, अभी भी इस पुस्तकालय लागू करने का फैसला के रूप में ब्याज बने रहे। यह ध्यान देने योग्य है कि इंटरनेट पर बड़ी संख्या में ऐसे पुस्तकालय हैं, लेकिन कहीं भी आईएल कोड में अभिव्यक्तियों के संकलन का चरण नहीं मिला है वास्तव में हर जगह व्याख्या है, जो के रूप में प्रभावी रूप में संकलन करने के लिए विरोध नहीं है, मार डाला। खैर, इसके अलावा, मैंने इसे खुद के लिए विशुद्ध रूप से विकसित किया, नई तकनीकों का अध्ययन करने के लिए, विशेष रूप से यह उम्मीद नहीं करता कि मेरे काम के परिणाम की आवश्यकता कहीं हो सकती है। अधीर के लिए: स्रोत कोड , कार्यक्रम ।

प्रयुक्त कार्यक्रम और पुस्तकालय

स्वर्ण पार्सिंग प्रणाली - व्याकरण लिखने और विभिन्न भाषाओं (सी, सी #, जावा, जावास्क्रिप्ट, ऑब्जेक्टिव-सी, पर्ल, पायथन, रूबी, आदि) के लिए व्याकरण और पार्सर्स के लिए कोड बनाने के लिए आईडीई। LALR पार्सिंग पर आधारित।
दृश्य स्टूडियो 2010
GOLD.Engine - विधानसभा नेट के तहत कनेक्शन, उत्पन्न की मेज के साथ बातचीत करने के लिए।
NUnit - ओपन पर्यावरण इकाई नेट के लिए आवेदन पत्र का परीक्षण।
ILSpy - .NET के लिए OpenSource disassembler।

चरण जिसके लिए मैंने पूरी प्रक्रिया को तोड़ दिया:

एक अभिव्यक्ति वृक्ष का निर्माण

मैंने गोल्ड पार्सर जनरेटर चुना, क्योंकि मेरे पास पहले से ही ANTLR के साथ अनुभव है और मुझे कुछ नया चाहिए था। लेकिन इसके फायदे को दूसरों के साथ तुलना में, आप देख सकते हैं इस तालिका में । जैसा कि आप देख सकते हैं, जब ANTLR के साथ तुलना की जाती है, तो GOLD एलएएलआर एल्गोरिथ्म पर आधारित है, एलएल नहीं। इसका मतलब यह है कि, सिद्धांत रूप में, उत्पन्न पार्सर तेज़ और अधिक शक्तिशाली है, लेकिन दूसरी ओर, इसे डीबग नहीं किया जा सकता है (स्वर्ण में, फ़ाइल को बाइनरी प्रारूप में डाउनलोड किया गया है), और यदि यह हो सकता है, तो यह पूरी तरह से अप्रयुक्त और असुविधाजनक होगा । एक और बड़ा अंतर एक व्याकरण काम के आकार है: BNF , नहीं EBNF । और इसका मतलब यह है कि इस रूप में दर्ज व्याकरण में कोण कोष्ठक, परिभाषा का संकेत और सशर्त घटनाओं और दोहराव की अनुपस्थिति ( विकी में अधिक) के अभाव के कारण थोड़ा बड़ा आकार है। उदाहरण के लिए, ईबीएनएफ में ऐसा नियम।

ExpressionList = Expression { ',' Expression }

इस रूप में फिर से लिखा जाएगा:

 <ExpressionList> ::= <ExpressionList> ',' <Expression> | <Expression>

तो, गणितीय अभिव्यक्तियों के अंतिम व्याकरण के निम्नलिखित रूप हैं:

गणितीय अभिव्यक्तियों का व्याकरण

 "Name" = 'Mathematics expressions' "Author" = 'Ivan Kochurkin' "Version" = '1.0' "About" = '' "Case Sensitive" = False "Start Symbol" = <Statements> Id = {Letter}{AlphaNumeric}* Number1 = {Digit}+('.'{Digit}*('('{Digit}*')')?)? Number2 = '.'{Digit}*('('{Digit}*')')? AddLiteral = '+' | '-' MultLiteral = '*' | '/' <Statements> ::= <Statements> <Devider> <Statement> | <Statements> <Devider> | <Statement> <Devider> ::= ';' | '.' <Statement> ::= <Expression> '=' <Expression> | <Expression> <Expression> ::= <FuncDef> | <Addition> <FuncDef> ::= Id '(' <ExpressionList> ')' | Id '' '(' <ExpressionList> ')' | Id '(' <ExpressionList> ')' '' <ExpressionList> ::= <ExpressionList> ',' <Expression> | <Expression> <Addition> ::= <Addition> AddLiteral <Multiplication> | <Addition> AddLiteral <FuncDef> | <FuncDef> AddLiteral <Multiplication> | <FuncDef> AddLiteral <FuncDef> | <Multiplication> <Multiplication> ::= <Multiplication> MultLiteral <Exponentiation> | <Multiplication> MultLiteral <FuncDef> | <FuncDef> MultLiteral <Exponentiation> | <FuncDef> MultLiteral <FuncDef> | <Exponentiation> <Exponentiation> ::= <Exponentiation> '^' <Negation> | <Exponentiation> '^' <FuncDef> | <FuncDef> '^' <Negation> | <FuncDef> '^' <FuncDef> | <Negation> <Negation> ::= AddLiteral <Value> | AddLiteral <FuncDef> | <Value> <Value> ::= Id | Number1 | Number2 | '(' <Expression> ')' | '|' <Expression> '|' | '(' <Expression> ')' '' | '|' <Expression> '|' '' | Id ''

व्याकरण में सब कुछ स्पष्ट प्रतीत होता है, टोकन को छोड़कर: नंबर 1 = {अंक} + ('।' {अंक} * ('(' {अंक} * ')')?)। 0.1234 (56) एक तर्कसंगत अंश है कि: 61111/495000 इस डिजाइन निम्नलिखित फार्म की लाइन विभाजित करने की अनुमति देता है। मैं बाद में इस तरह के स्ट्रिंग को एक अंश में परिवर्तित करने के बारे में बात करूंगा।

इसलिए, संकलित व्याकरण तालिकाओं (संकलित व्याकरण तालिका फ़ाइल) उत्पन्न होने के बाद, और पार्सर वर्ग रूपरेखा बनाई जाती है, एक उपयुक्त एएसटी पेड़ बनाने के लिए उत्तरार्द्ध को संशोधित करना आवश्यक है। इस मामले में पार्सर क्लास फ्रेमवर्क एक .cs फ़ाइल है जिसमें व्याकरण के सभी नियमों के माध्यम से एक लूप होता है, टोकन और अन्य त्रुटियों के गलत अनुक्रम के मामले में अपवाद से निपटने (वैसे, गोल्ड में भी ऐसे फ्रेमवर्क के अलग-अलग जनरेटर हैं, और मैंने Cook .NET को चुना है। )। तो, हमारे मामले में, "उपयुक्त" का अर्थ है एक पेड़ जिसमें नोड्स होते हैं जो प्रकार हो सकते हैं:

परिकलित - संकलक के लिए स्वीकार्य दोहरे प्रारूप में परिकलित स्थिरांक का प्रतिनिधित्व करने वाला नोड, उदाहरण के लिए, "0.714285714285714", "0.122222222222222"। प्रत्येक ऐसे स्थिरांक के लिए एक नई वस्तु बनाई जाती है, भले ही वे समान हों।
मूल्य - एक परिमेय अंश के प्रारूप में परिकलित स्थिरांक का प्रतिनिधित्व करने वाला नोड, अर्थात एक "11/90" के रूप में, ".1234" - - "के रूप में 617/5000" 1 "1.1", "0.1 (2)" के रूप में प्रतिनिधित्व किया है। प्रत्येक ऐसे स्थिरांक के लिए एक नई वस्तु बनाई जाती है, भले ही वे समान हों।
निरंतर - एक नोड जो अपरिभाषित स्थिर का प्रतिनिधित्व करता है, उदाहरण के लिए, "a", "b", आदि। यदि दो ऐसे स्थिरांक एक अभिव्यक्ति में पाए जाते हैं, तो वे एक नोड को इंगित करते हैं।
चर - एक चर का प्रतिनिधित्व करने वाला एक नोड, उदाहरण के लिए, "x", "y", आदि। यदि एक निश्चित चर एक अभिव्यक्ति में कई बार होता है, तो इसके लिए केवल एक वस्तु बनाई जाती है, साथ ही साथ एक अपरिभाषित स्थिर भी। यह समझना महत्वपूर्ण है कि एक स्थिर और एक चर के बीच का अंतर केवल विश्लेषणात्मक व्युत्पन्न की व्युत्पत्ति के चरण में महत्वपूर्ण है, और अन्य मामलों में यह ज्ञान आवश्यक नहीं है।
फ़ंक्शन - एक नोड एक फ़ंक्शन का प्रतिनिधित्व करता है, उदाहरण के लिए, "+", "पाप", "^" और अन्य। एकमात्र नोड जिसमें बच्चे हो सकते हैं।

सभी प्रकार के नोड्स को स्पष्ट रूप से चित्र में दिखाया गया है:

यह व्याकरण से देखा जा सकता है कि परिणामी पेड़ के नोड्स में या तो कोई बच्चे नहीं हैं (उदाहरण के लिए, मान या चर), या मानक कार्यों के मामले में एक से दो बच्चे हैं (उदाहरण के लिए, कॉस, जोड़, घातांक)। अन्य सभी कार्यों में अधिक तर्क हो सकते हैं, लेकिन उन पर विचार नहीं किया गया।

इस प्रकार, सभी नोड्स (या फ़ंक्शंस के साथ नोड्स) 0 से 2 बच्चे, समावेशी हैं। यह एक सैद्धांतिक दृष्टिकोण से सच है। लेकिन वास्तव में, मैं समारोह करना था "+" और "*" आदेश सरलीकरण का कार्य है, जो बाद में चर्चा की जाएगी की सुविधा के लिए बच्चों की एक असीमित संख्या है। वैसे, "-" और "/" जैसे द्विआधारी संचालन को भी उन्हीं कारणों के लिए छोड़ना पड़ा (वे सही पक्ष की उपेक्षा के साथ और दाहिनी ओर के उलट के साथ गुणा के साथ बदल दिए गए थे)।

तो, पार्सिंग स्टेज पर, प्रत्येक नियम के लिए सभी नोड्स गिर जाते हैं या नोड्स नामक बफर से पुनर्प्राप्त होते हैं। इस प्रकार, पूरी प्रक्रिया के अंत में, दाएं और बाएं भागों के साथ एक या एक से अधिक कार्य इस बफर में रहते हैं। इसके अलावा, पार्सिंग की प्रक्रिया में, ताकि जोड़ और गुणा कार्यों को तुरंत बहुराष्ट्रीय बनाया जाता है, अतिरिक्त बफ़र्स ArgsCount और ArgsFuncTypes का उपयोग किया गया था जो क्रमशः फ़ंक्शन और वर्तमान फ़ंक्शन के प्रकार में तर्कों की संख्या को संग्रहीत करते हैं। इस प्रकार, उदाहरण के लिए, गुणन फ़ंक्शन के लिए, इस कोड का उपयोग किया जाता है:

पहला गुणक प्रसंस्करण:

 // <Multiplication> ::= <Exponentiation> if (MultiplicationMultiChilds) PushFunc(KnownMathFunctionType.Mult);

आई-वें गुणक का प्रसंस्करण:

 // <Multiplication> ::= <Multiplication> MultLiteral <Exponentiation> // <Multiplication> ::= <Multiplication> MultLiteral <FuncDef> if (KnownMathFunction.BinaryNamesFuncs[r[1].Data.ToString()] == KnownMathFunctionType.Div) Nodes.Push(new FuncNode(KnownMathFunctionType.Exp, new MathFuncNode[] { Nodes.Pop(), new ValueNode(-1) })); ArgsCount[ArgsCount.Count - 1]++;

अंतिम गुणक को संसाधित करना:

 // <Addition> ::= <Multiplication> if (MultiplicationMultiChilds) PushOrRemoveFunc(KnownMathFunctionType.Mult); if (AdditionMultiChilds) PushFunc(KnownMathFunctionType.Add);

इस कोड से, यह स्पष्ट है कि, उदाहरण के लिए, शून्य तत्वों के साथ कोई गुणन और नहीं पिछले गुणा समारोह PushOrRemoveFunc का उपयोग कर हटा दिया जाना चाहिए अगर है। इसी तरह की कार्रवाइयों को जोड़ने की जरूरत है।

एक चर, द्विआधारी काम करता है, स्थिरांक, चर और मानों के कार्यों का संसाधन तुच्छ है, और कहा कि तुम सब MathExprParser.cs में देख सकते हैं।

विश्लेषणात्मक व्युत्पन्न की गणना

इस स्तर पर, आपको फ़ंक्शन को इसके व्युत्पन्न में बदलने की आवश्यकता है।

जैसा कि आप पहले चरण से जानते हैं, निर्मित अभिव्यक्ति के पेड़ में केवल चार प्रकार के नोड होते हैं (पांचवें बाद में प्रकट होता है)। उनके लिए, हम व्युत्पन्न को परिभाषित करते हैं:

मान '= 0
लगातार '= 0
चर ’= १
समारोह '= अणु [समारोह]

मुझे समझाएं: व्युत्पन्न फ़ंक्शन के लिए, आपको पहले से तैयार सारणीबद्ध मान लेने की आवश्यकता है, और यह कुछ कठिनाइयों का कारण बनता है, क्योंकि इस मूल्य के अंदर भी डेरिवेटिव हैं, अर्थात्। प्रक्रिया प्रकृति में पुनरावर्ती है। आप नीचे दिए गए स्पॉइलर के नीचे ऐसे कार्यान्वित प्रतिस्थापनों की पूरी सूची देख सकते हैं।

डेरिवेटिव की सूची

 (f(x) ^ g(x))' = f(x) ^ g(x) * (f(x)' * g(x) / f(x) + g(x)' * ln(f(x)));"); neg(f(x))' = neg(f(x)');"); sin(f(x))' = cos(f(x)) * f(x)'; cos(f(x))' = -sin(f(x)) * f(x)'; tan(f(x))' = f(x)' / cos(f(x)) ^ 2; cot(f(x))' = -f(x)' / sin(f(x)) ^ 2; arcsin(f(x))' = f(x)' / sqrt(1 - f(x) ^ 2); arccos(f(x))' = -f(x)' / sqrt(1 - f(x) ^ 2); arctan(f(x))' = f(x)' / (1 + f(x) ^ 2); arccot(f(x))' = -f(x)' / (1 + f(x) ^ 2); sinh(f(x))' = f(x)' * cosh(x); cosh(f(x))' = f(x)' * sinh(x); arcsinh(f(x))' = f(x)' / sqrt(f(x) ^ 2 + 1); arcosh(f(x))' = f(x)' / sqrt(f(x) ^ 2 - 1); ln(f(x))' = f(x)' / f(x); log(f(x), g(x))' = g'(x)/(g(x)*ln(f(x))) - (f'(x)*ln(g(x)))/(f(x)*ln(f(x))^2);

यह ध्यान देने योग्य है कि सभी डेरिवेटिव कोड में कठिन नहीं लिखे गए हैं, लेकिन गतिशील रूप से भी दर्ज किए जा सकते हैं और पार्स किए जा सकते हैं।

इस सूची में कोई जोड़ या गुणा नहीं है, क्योंकि जैसा कि ऊपर उल्लेख किया गया है, ये कई तर्कों के साथ कार्य करते हैं। और ऐसे नियमों को पार्स करने के लिए, बहुत सारे कोड लिखना आवश्यक होगा। समान कारणों से, कार्यों की कोई रचना नहीं है, अर्थात्। (एफ (g (x))) '= च (g (x))' * g (x) ', और बदले सभी कार्यों की रचना के कार्य के रूप में प्रस्तुत कर रहे हैं।

इसके अलावा, यदि फंक्शन को डेरिवेटिव्स (यानी एक अपरिभाषित फ़ंक्शन) के लिए प्रतिस्थापन नहीं मिला, तो यह केवल एक स्ट्रोक के साथ एक फ़ंक्शन द्वारा प्रतिस्थापित किया जाता है: i.e. f (x) f (x) 'में बदल जाएगा।

विश्लेषणात्मक व्युत्पन्न सफलतापूर्वक प्राप्त किए जाने के बाद, समस्या यह उठती है कि परिणामस्वरूप अभिव्यक्ति में बहुत सारा "कचरा" है, जैसे कि + 0, * 1 *, * a ^ -1, इत्यादि। इसके अलावा, परिणामस्वरूप अभिव्यक्ति की गणना अधिक इष्टतम तरीके से की जा सकती है। उदाहरण के लिए, यहां तक कि एक साधारण अभिव्यक्ति के लिए, आपको एक बदसूरत अभिव्यक्ति मिलती है:

 (x^2 + 2)' = 0 + 2 * 1 * x ^ 1

सरलीकरण का उपयोग ऐसी कमियों को दूर करने के लिए किया जाता है।

अभिव्यक्ति का सरलीकरण

इस स्तर पर, डेरिवेटिव की गणना के चरण के विपरीत, मैंने उनके बाद के विश्लेषण के लिए एक अलग जगह में सादगी के नियमों को नहीं लिखा, क्योंकि जोड़ और गुणा का कार्य कई तर्कों के कार्य हैं, जो इस तरह के नियमों को बनाने में एक निश्चित कठिनाई प्रस्तुत करता है। एक पुनरावृत्त भाषा का संदर्भ।

विषय की शुरुआत में, मैंने इस विषय पर छुआ कि क्यों जोड़ और गुणा को एन-आर्य कार्यों के रूप में दर्शाया गया है। नीचे दी गई तस्वीर में दिखाए गए स्थिति की कल्पना करें। यहाँ हम देखते हैं कि a -a संक्षिप्त है। लेकिन बाइनरी फ़ंक्शन के मामले में यह कैसे करें? ऐसा करने के लिए, नोड्स ए , बी, और सी पर पुनरावृत्त करें ताकि बाद में पता चले कि ए और -ए एक ही नोड के बच्चे हैं, जिसका अर्थ है कि वे नोड के साथ एक साथ कम हो सकते हैं। लेकिन, ज़ाहिर है, पेड़ों को छांटना इतना आसान काम नहीं है, क्योंकि एक ही बार में सभी बच्चों के साथ एक चक्र में सभी क्रियाओं को करना बहुत आसान है, जैसा कि दाईं ओर की आकृति में दिखाया गया है। वैसे, इस तरह के एक संश्लिष्टता से हमें समरूपता और संयमता के गणितीय गुणों को बनाने की अनुमति मिलती है।

सरलीकरण प्रक्रिया के दौरान, दो नोड्स की तुलना करने में समस्या उत्पन्न होती है, जो बदले में, चार प्रकारों में से एक हो सकती है। उदाहरण के लिए, पाप (x + y) और -sin (x + y) जैसे भावों को कम करने के लिए यह आवश्यक है। यह स्पष्ट है कि आप नोड्स द्वारा स्वयं और उनके सभी वंशों की तुलना कर सकते हैं। लेकिन समस्या यह है कि यह विधि उस स्थिति का सामना नहीं करेगी जब शर्तों या कारकों को फिर से व्यवस्थित किया जाता है, उदाहरण के लिए, पाप (x + y) और -sin (y + x)। क्रमविनिमेयता (जैसे कि, जोड़ और घटाव) जिसके लिए इस समस्या को शब्दों या कारकों presorting का उपयोग करता है हल करने के लिए। नोड्स की तुलना नीचे चित्र में दिखाई गई है, अर्थात मान स्थिरांक से कम हैं, स्थिरांक चर से कम हैं, आदि। फ़ंक्शंस के लिए, सब कुछ थोड़ा और अधिक जटिल है, क्योंकि आपको न केवल उनके नामों की तुलना करने की आवश्यकता है, बल्कि तर्कों की संख्या और स्वयं तर्क भी।

इस प्रकार, उपरोक्त सभी रूपांतरणों और गणनाओं के बाद, मूल अभिव्यक्ति काफी अच्छी तरह से सरल हो गई है।

तर्कसंगत अंश प्रसंस्करण

मुझे जो तर्कसंगत कार्यान्वयन मिला, उसमें सामान्य स्ट्रिंग प्रकार का कोई रूपांतरण नहीं था, उदाहरण के लिए 0.666666, एक विशिष्ट अंश और हर के साथ एक भिन्न प्रकार में, अर्थात्। एक निश्चित सटीकता के साथ 2/3 में। फिर मैंने अपने कार्यान्वयन को बहुत सारे विकल्पों के साथ लिखने का फैसला किया। उदाहरण के लिए, नीचे दिए गए कार्य यह निर्धारित करते हैं कि क्या एक निश्चित संख्या विशुद्ध रूप से अपरिमेय है, या क्या इसकी अवधि या परिमित अंश है और इसे एक परिमेय में परिवर्तित किया जा सकता है, उदाहरण के लिए, पाप (pi) एक निश्चित सटीकता के साथ। सामान्य तौर पर, stackoverflow.com के मेरे उत्तर में अन्य विवरण देखें। विधि का एक संक्षिप्त चित्रमय विवरण नीचे दिए गए चित्र में प्रस्तुत किया गया है, और कोड नीचे सूची में है। यह ध्यान देने योग्य है कि, फिर भी, मानक गणितीय कार्यों की सटीकता और दोहरे प्रकार तर्कसंगत और वास्तविक संख्याओं की सामान्य मान्यता के लिए पर्याप्त नहीं है, लेकिन सैद्धांतिक रूप से सब कुछ काम करता है।

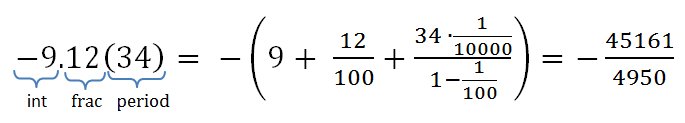
दशमलव को अंश में बदलें

 /// <summary> /// Convert decimal to fraction /// </summary> /// <param name="value">decimal value to convert</param> /// <param name="result">result fraction if conversation is succsess</param> /// <param name="decimalPlaces">precision of considereation frac part of value</param> /// <param name="trimZeroes">trim zeroes on the right part of the value or not</param> /// <param name="minPeriodRepeat">minimum period repeating</param> /// <param name="digitsForReal">precision for determination value to real if period has not been founded</param> /// <returns></returns> public static bool FromDecimal(decimal value, out Rational<T> result, int decimalPlaces = 28, bool trimZeroes = false, decimal minPeriodRepeat = 2, int digitsForReal = 9) { var valueStr = value.ToString("0.0000000000000000000000000000", CultureInfo.InvariantCulture); var strs = valueStr.Split('.'); long intPart = long.Parse(strs[0]); string fracPartTrimEnd = strs[1].TrimEnd(new char[] { '0' }); string fracPart; if (trimZeroes) { fracPart = fracPartTrimEnd; decimalPlaces = Math.Min(decimalPlaces, fracPart.Length); } else fracPart = strs[1]; result = new Rational<T>(); try { string periodPart; bool periodFound = false; int i; for (i = 0; i < fracPart.Length; i++) { if (fracPart[i] == '0' && i != 0) continue; for (int j = i + 1; j < fracPart.Length; j++) { periodPart = fracPart.Substring(i, j - i); periodFound = true; decimal periodRepeat = 1; decimal periodStep = 1.0m / periodPart.Length; var upperBound = Math.Min(fracPart.Length, decimalPlaces); int k; for (k = i + periodPart.Length; k < upperBound; k += 1) { if (periodPart[(k - i) % periodPart.Length] != fracPart[k]) { periodFound = false; break; } periodRepeat += periodStep; } if (!periodFound && upperBound - k <= periodPart.Length && periodPart[(upperBound - i) % periodPart.Length] > '5') { var ind = (k - i) % periodPart.Length; var regroupedPeriod = (periodPart.Substring(ind) + periodPart.Remove(ind)).Substring(0, upperBound - k); ulong periodTailPlusOne = ulong.Parse(regroupedPeriod) + 1; ulong fracTail = ulong.Parse(fracPart.Substring(k, regroupedPeriod.Length)); if (periodTailPlusOne == fracTail) periodFound = true; } if (periodFound && periodRepeat >= minPeriodRepeat) { result = FromDecimal(strs[0], fracPart.Substring(0, i), periodPart); break; } else periodFound = false; } if (periodFound) break; } if (!periodFound) { if (fracPartTrimEnd.Length >= digitsForReal) return false; else { result = new Rational<T>(long.Parse(strs[0]), 1, false); if (fracPartTrimEnd.Length != 0) result = new Rational<T>(ulong.Parse(fracPartTrimEnd), TenInPower(fracPartTrimEnd.Length)); return true; } } return true; } catch { return false; } } public static Rational<T> FromDecimal(string intPart, string fracPart, string periodPart) { Rational<T> firstFracPart; if (fracPart != null && fracPart.Length != 0) { ulong denominator = TenInPower(fracPart.Length); firstFracPart = new Rational<T>(ulong.Parse(fracPart), denominator); } else firstFracPart = new Rational<T>(0, 1, false); Rational<T> secondFracPart; if (periodPart != null && periodPart.Length != 0) secondFracPart = new Rational<T>(ulong.Parse(periodPart), TenInPower(fracPart.Length)) * new Rational<T>(1, Nines((ulong)periodPart.Length), false); else secondFracPart = new Rational<T>(0, 1, false); var result = firstFracPart + secondFracPart; if (intPart != null && intPart.Length != 0) { long intPartLong = long.Parse(intPart); result = new Rational<T>(intPartLong, 1, false) + (intPartLong == 0 ? 1 : Math.Sign(intPartLong)) * result; } return result; } private static ulong TenInPower(int power) { ulong result = 1; for (int l = 0; l < power; l++) result *= 10; return result; } private static decimal TenInNegPower(int power) { decimal result = 1; for (int l = 0; l > power; l--) result /= 10.0m; return result; } private static ulong Nines(ulong power) { ulong result = 9; if (power >= 0) for (ulong l = 0; l < power - 1; l++) result = result * 10 + 9; return result; } = /// <summary> /// Convert decimal to fraction /// </summary> /// <param name="value">decimal value to convert</param> /// <param name="result">result fraction if conversation is succsess</param> /// <param name="decimalPlaces">precision of considereation frac part of value</param> /// <param name="trimZeroes">trim zeroes on the right part of the value or not</param> /// <param name="minPeriodRepeat">minimum period repeating</param> /// <param name="digitsForReal">precision for determination value to real if period has not been founded</param> /// <returns></returns> public static bool FromDecimal(decimal value, out Rational<T> result, int decimalPlaces = 28, bool trimZeroes = false, decimal minPeriodRepeat = 2, int digitsForReal = 9) { var valueStr = value.ToString("0.0000000000000000000000000000", CultureInfo.InvariantCulture); var strs = valueStr.Split('.'); long intPart = long.Parse(strs[0]); string fracPartTrimEnd = strs[1].TrimEnd(new char[] { '0' }); string fracPart; if (trimZeroes) { fracPart = fracPartTrimEnd; decimalPlaces = Math.Min(decimalPlaces, fracPart.Length); } else fracPart = strs[1]; result = new Rational<T>(); try { string periodPart; bool periodFound = false; int i; for (i = 0; i < fracPart.Length; i++) { if (fracPart[i] == '0' && i != 0) continue; for (int j = i + 1; j < fracPart.Length; j++) { periodPart = fracPart.Substring(i, j - i); periodFound = true; decimal periodRepeat = 1; decimal periodStep = 1.0m / periodPart.Length; var upperBound = Math.Min(fracPart.Length, decimalPlaces); int k; for (k = i + periodPart.Length; k < upperBound; k += 1) { if (periodPart[(k - i) % periodPart.Length] != fracPart[k]) { periodFound = false; break; } periodRepeat += periodStep; } if (!periodFound && upperBound - k <= periodPart.Length && periodPart[(upperBound - i) % periodPart.Length] > '5') { var ind = (k - i) % periodPart.Length; var regroupedPeriod = (periodPart.Substring(ind) + periodPart.Remove(ind)).Substring(0, upperBound - k); ulong periodTailPlusOne = ulong.Parse(regroupedPeriod) + 1; ulong fracTail = ulong.Parse(fracPart.Substring(k, regroupedPeriod.Length)); if (periodTailPlusOne == fracTail) periodFound = true; } if (periodFound && periodRepeat >= minPeriodRepeat) { result = FromDecimal(strs[0], fracPart.Substring(0, i), periodPart); break; } else periodFound = false; } if (periodFound) break; } if (!periodFound) { if (fracPartTrimEnd.Length >= digitsForReal) return false; else { result = new Rational<T>(long.Parse(strs[0]), 1, false); if (fracPartTrimEnd.Length != 0) result = new Rational<T>(ulong.Parse(fracPartTrimEnd), TenInPower(fracPartTrimEnd.Length)); return true; } } return true; } catch { return false; } } public static Rational<T> FromDecimal(string intPart, string fracPart, string periodPart) { Rational<T> firstFracPart; if (fracPart != null && fracPart.Length != 0) { ulong denominator = TenInPower(fracPart.Length); firstFracPart = new Rational<T>(ulong.Parse(fracPart), denominator); } else firstFracPart = new Rational<T>(0, 1, false); Rational<T> secondFracPart; if (periodPart != null && periodPart.Length != 0) secondFracPart = new Rational<T>(ulong.Parse(periodPart), TenInPower(fracPart.Length)) * new Rational<T>(1, Nines((ulong)periodPart.Length), false); else secondFracPart = new Rational<T>(0, 1, false); var result = firstFracPart + secondFracPart; if (intPart != null && intPart.Length != 0) { long intPartLong = long.Parse(intPart); result = new Rational<T>(intPartLong, 1, false) + (intPartLong == 0 ? 1 : Math.Sign(intPartLong)) * result; } return result; } private static ulong TenInPower(int power) { ulong result = 1; for (int l = 0; l < power; l++) result *= 10; return result; } private static decimal TenInNegPower(int power) { decimal result = 1; for (int l = 0; l > power; l--) result /= 10.0m; return result; } private static ulong Nines(ulong power) { ulong result = 9; if (power >= 0) for (ulong l = 0; l < power - 1; l++) result = result * 10 + 9; return result; } , CultureInfo.InvariantCulture); /// <summary> /// Convert decimal to fraction /// </summary> /// <param name="value">decimal value to convert</param> /// <param name="result">result fraction if conversation is succsess</param> /// <param name="decimalPlaces">precision of considereation frac part of value</param> /// <param name="trimZeroes">trim zeroes on the right part of the value or not</param> /// <param name="minPeriodRepeat">minimum period repeating</param> /// <param name="digitsForReal">precision for determination value to real if period has not been founded</param> /// <returns></returns> public static bool FromDecimal(decimal value, out Rational<T> result, int decimalPlaces = 28, bool trimZeroes = false, decimal minPeriodRepeat = 2, int digitsForReal = 9) { var valueStr = value.ToString("0.0000000000000000000000000000", CultureInfo.InvariantCulture); var strs = valueStr.Split('.'); long intPart = long.Parse(strs[0]); string fracPartTrimEnd = strs[1].TrimEnd(new char[] { '0' }); string fracPart; if (trimZeroes) { fracPart = fracPartTrimEnd; decimalPlaces = Math.Min(decimalPlaces, fracPart.Length); } else fracPart = strs[1]; result = new Rational<T>(); try { string periodPart; bool periodFound = false; int i; for (i = 0; i < fracPart.Length; i++) { if (fracPart[i] == '0' && i != 0) continue; for (int j = i + 1; j < fracPart.Length; j++) { periodPart = fracPart.Substring(i, j - i); periodFound = true; decimal periodRepeat = 1; decimal periodStep = 1.0m / periodPart.Length; var upperBound = Math.Min(fracPart.Length, decimalPlaces); int k; for (k = i + periodPart.Length; k < upperBound; k += 1) { if (periodPart[(k - i) % periodPart.Length] != fracPart[k]) { periodFound = false; break; } periodRepeat += periodStep; } if (!periodFound && upperBound - k <= periodPart.Length && periodPart[(upperBound - i) % periodPart.Length] > '5') { var ind = (k - i) % periodPart.Length; var regroupedPeriod = (periodPart.Substring(ind) + periodPart.Remove(ind)).Substring(0, upperBound - k); ulong periodTailPlusOne = ulong.Parse(regroupedPeriod) + 1; ulong fracTail = ulong.Parse(fracPart.Substring(k, regroupedPeriod.Length)); if (periodTailPlusOne == fracTail) periodFound = true; } if (periodFound && periodRepeat >= minPeriodRepeat) { result = FromDecimal(strs[0], fracPart.Substring(0, i), periodPart); break; } else periodFound = false; } if (periodFound) break; } if (!periodFound) { if (fracPartTrimEnd.Length >= digitsForReal) return false; else { result = new Rational<T>(long.Parse(strs[0]), 1, false); if (fracPartTrimEnd.Length != 0) result = new Rational<T>(ulong.Parse(fracPartTrimEnd), TenInPower(fracPartTrimEnd.Length)); return true; } } return true; } catch { return false; } } public static Rational<T> FromDecimal(string intPart, string fracPart, string periodPart) { Rational<T> firstFracPart; if (fracPart != null && fracPart.Length != 0) { ulong denominator = TenInPower(fracPart.Length); firstFracPart = new Rational<T>(ulong.Parse(fracPart), denominator); } else firstFracPart = new Rational<T>(0, 1, false); Rational<T> secondFracPart; if (periodPart != null && periodPart.Length != 0) secondFracPart = new Rational<T>(ulong.Parse(periodPart), TenInPower(fracPart.Length)) * new Rational<T>(1, Nines((ulong)periodPart.Length), false); else secondFracPart = new Rational<T>(0, 1, false); var result = firstFracPart + secondFracPart; if (intPart != null && intPart.Length != 0) { long intPartLong = long.Parse(intPart); result = new Rational<T>(intPartLong, 1, false) + (intPartLong == 0 ? 1 : Math.Sign(intPartLong)) * result; } return result; } private static ulong TenInPower(int power) { ulong result = 1; for (int l = 0; l < power; l++) result *= 10; return result; } private static decimal TenInNegPower(int power) { decimal result = 1; for (int l = 0; l > power; l--) result /= 10.0m; return result; } private static ulong Nines(ulong power) { ulong result = 9; if (power >= 0) for (ulong l = 0; l < power - 1; l++) result = result * 10 + 9; return result; } , regroupedPeriod.Length)); /// <summary> /// Convert decimal to fraction /// </summary> /// <param name="value">decimal value to convert</param> /// <param name="result">result fraction if conversation is succsess</param> /// <param name="decimalPlaces">precision of considereation frac part of value</param> /// <param name="trimZeroes">trim zeroes on the right part of the value or not</param> /// <param name="minPeriodRepeat">minimum period repeating</param> /// <param name="digitsForReal">precision for determination value to real if period has not been founded</param> /// <returns></returns> public static bool FromDecimal(decimal value, out Rational<T> result, int decimalPlaces = 28, bool trimZeroes = false, decimal minPeriodRepeat = 2, int digitsForReal = 9) { var valueStr = value.ToString("0.0000000000000000000000000000", CultureInfo.InvariantCulture); var strs = valueStr.Split('.'); long intPart = long.Parse(strs[0]); string fracPartTrimEnd = strs[1].TrimEnd(new char[] { '0' }); string fracPart; if (trimZeroes) { fracPart = fracPartTrimEnd; decimalPlaces = Math.Min(decimalPlaces, fracPart.Length); } else fracPart = strs[1]; result = new Rational<T>(); try { string periodPart; bool periodFound = false; int i; for (i = 0; i < fracPart.Length; i++) { if (fracPart[i] == '0' && i != 0) continue; for (int j = i + 1; j < fracPart.Length; j++) { periodPart = fracPart.Substring(i, j - i); periodFound = true; decimal periodRepeat = 1; decimal periodStep = 1.0m / periodPart.Length; var upperBound = Math.Min(fracPart.Length, decimalPlaces); int k; for (k = i + periodPart.Length; k < upperBound; k += 1) { if (periodPart[(k - i) % periodPart.Length] != fracPart[k]) { periodFound = false; break; } periodRepeat += periodStep; } if (!periodFound && upperBound - k <= periodPart.Length && periodPart[(upperBound - i) % periodPart.Length] > '5') { var ind = (k - i) % periodPart.Length; var regroupedPeriod = (periodPart.Substring(ind) + periodPart.Remove(ind)).Substring(0, upperBound - k); ulong periodTailPlusOne = ulong.Parse(regroupedPeriod) + 1; ulong fracTail = ulong.Parse(fracPart.Substring(k, regroupedPeriod.Length)); if (periodTailPlusOne == fracTail) periodFound = true; } if (periodFound && periodRepeat >= minPeriodRepeat) { result = FromDecimal(strs[0], fracPart.Substring(0, i), periodPart); break; } else periodFound = false; } if (periodFound) break; } if (!periodFound) { if (fracPartTrimEnd.Length >= digitsForReal) return false; else { result = new Rational<T>(long.Parse(strs[0]), 1, false); if (fracPartTrimEnd.Length != 0) result = new Rational<T>(ulong.Parse(fracPartTrimEnd), TenInPower(fracPartTrimEnd.Length)); return true; } } return true; } catch { return false; } } public static Rational<T> FromDecimal(string intPart, string fracPart, string periodPart) { Rational<T> firstFracPart; if (fracPart != null && fracPart.Length != 0) { ulong denominator = TenInPower(fracPart.Length); firstFracPart = new Rational<T>(ulong.Parse(fracPart), denominator); } else firstFracPart = new Rational<T>(0, 1, false); Rational<T> secondFracPart; if (periodPart != null && periodPart.Length != 0) secondFracPart = new Rational<T>(ulong.Parse(periodPart), TenInPower(fracPart.Length)) * new Rational<T>(1, Nines((ulong)periodPart.Length), false); else secondFracPart = new Rational<T>(0, 1, false); var result = firstFracPart + secondFracPart; if (intPart != null && intPart.Length != 0) { long intPartLong = long.Parse(intPart); result = new Rational<T>(intPartLong, 1, false) + (intPartLong == 0 ? 1 : Math.Sign(intPartLong)) * result; } return result; } private static ulong TenInPower(int power) { ulong result = 1; for (int l = 0; l < power; l++) result *= 10; return result; } private static decimal TenInNegPower(int power) { decimal result = 1; for (int l = 0; l > power; l--) result /= 10.0m; return result; } private static ulong Nines(ulong power) { ulong result = 9; if (power >= 0) for (ulong l = 0; l < power - 1; l++) result = result * 10 + 9; return result; }

अभिव्यक्ति संकलन

सादगी के चरण के बाद परिणामी अर्थ वृक्ष को IL कोड में बदलने के लिए, मैंने Mono.Cecil का उपयोग किया।

प्रक्रिया की शुरुआत में, एक असेंबली, वर्ग और विधि बनाई जाती है जिसमें कमांड लिखे जाएंगे। फिर, प्रत्येक फ़नकोड के लिए, यह गणना की जाती है कि यह कार्यक्रम में कितनी बार दिखाई देता है। उदाहरण के लिए, यदि कोई फ़ंक्शन पाप (x ^ 2) * cos (x ^ 2) है , तो इसमें x को 2 की शक्ति तक बढ़ाने का कार्य दो बार होता है, और फ़ंक्शन sin और cos - one at a। बाद में, दर गणना समारोह के बारे में जानकारी निम्नलिखित तरीके (अर्थात, जिससे दूसरी बार एक ही समारोह जगह नहीं ले करता है की गणना) का उपयोग करता है:

 if (!func.Calculated) { EmitFunc(funcNode); func.Calculated = true; } else IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));

इस सभी कोड को जनरेट करने के बाद, IL कोड की कुछ अन्य अनुकूलन संभव हैं, जैसा कि नीचे दिए गए चित्र में दिखाया गया है।

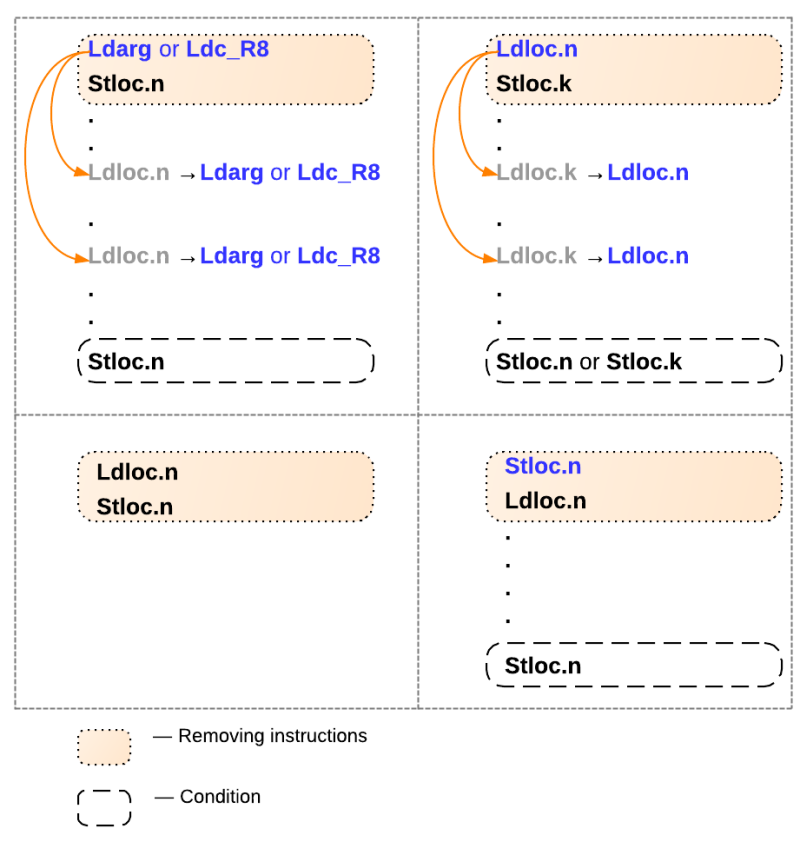
इस तस्वीर में:

Ldarg - स्टैक पर एक विशिष्ट फ़ंक्शन तर्क लोड करने का संचालन।
Ldc_R8 - स्टैक पर एक विशिष्ट डबल मान लोड हो रहा है।
Stloc.n - स्टैक से अंतिम मान प्राप्त करें और इसे स्थानीय चर n में संग्रहीत करें।
Ldloc.n - स्टैक पर स्थानीय चर n को धक्का देना ।

यदि कुछ शर्तों को पूरा किया जाता है, तो बेज बॉक्स के निर्देशों को हटाया जा सकता है। उदाहरण के लिए, ऊपरी बाईं छवि में मामला निम्नानुसार वर्णित है: यदि वर्तमान निर्देश किसी फ़ंक्शन से एक तर्क लोड कर रहा है या एक निरंतर लोड हो रहा है, और अगला निर्देश इसे स्थानीय चर n में सहेज रहा है, तो लोडिंग के साथ स्थानीय चर n के लोड निर्देशों को प्रतिस्थापित करके निर्देशों के इस ब्लॉक को हटाया जा सकता है फ़ंक्शन तर्क या निरंतर लोड हो रहा है। प्रतिस्थापन प्रक्रिया को तब तक जारी रखें जब तक कि स्थानीय वेरिएबल n में पहला सेव स्टेटमेंट न हो जाए । अन्य तीन मामलों को इसी तरह से समझाया गया है। उदाहरण के लिए, अनुक्रम Ldloc.n ; Stloc.n को तुरंत हटाया जा सकता है।

यह ध्यान दिया जाना चाहिए कि डेटा अनुकूलन कोड में शाखाओं के अभाव में लागू होते हैं, और यह स्पष्ट है क्यों (अगर काफी स्पष्ट नहीं है, मैं सोच सुझाव है)। लेकिन चूंकि गणितीय क्रियाओं और उनके व्युत्पन्न के कोड में मेरे मामले में चक्र शामिल नहीं हो सकते, इसलिए यह सब काम करता है।

तेजी से घातांक

मुझे लगता है कि एक शक्ति को जल्दी से बढ़ाने के लिए एल्गोरिथ्म के बारे में लगभग सभी जानते हैं। लेकिन इस एल्गोरिथ्म के नीचे संकलन स्तर पर प्रस्तुत किया गया है:

आईएल कोड में तेजी से घातांक एल्गोरिथ्म लागू किया गया

 if (power <= 3) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); for (int i = 1; i < power; i++) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } } else if (power == 4) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } else { // result: funcNode.Number // x: funcNode.Number + 1 //int result = x; IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); power--; do { if ((power & 1) == 1) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } if (power <= 1) break; //x = x * x; IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); power = power >> 1; } while (power != 0); } + if (power <= 3) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); for (int i = 1; i < power; i++) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } } else if (power == 4) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } else { // result: funcNode.Number // x: funcNode.Number + 1 //int result = x; IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); power--; do { if ((power & 1) == 1) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } if (power <= 1) break; //x = x * x; IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); power = power >> 1; } while (power != 0); } + if (power <= 3) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); for (int i = 1; i < power; i++) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } } else if (power == 4) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } else { // result: funcNode.Number // x: funcNode.Number + 1 //int result = x; IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); power--; do { if ((power & 1) == 1) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } if (power <= 1) break; //x = x * x; IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); power = power >> 1; } while (power != 0); } + if (power <= 3) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); for (int i = 1; i < power; i++) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } } else if (power == 4) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } else { // result: funcNode.Number // x: funcNode.Number + 1 //int result = x; IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); power--; do { if ((power & 1) == 1) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } if (power <= 1) break; //x = x * x; IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); power = power >> 1; } while (power != 0); } + if (power <= 3) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); for (int i = 1; i < power; i++) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } } else if (power == 4) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } else { // result: funcNode.Number // x: funcNode.Number + 1 //int result = x; IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); power--; do { if ((power & 1) == 1) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } if (power <= 1) break; //x = x * x; IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); power = power >> 1; } while (power != 0); }

यह ध्यान देने योग्य है कि तेज घातांक एल्गोरिथ्म सबसे इष्टतम प्रतिपादक एल्गोरिथ्म नहीं है। उदाहरण के लिए, निम्नलिखित दो तरीकों से पांच बार समान चर का गुणन है। मेरे लिए भी x ^ 4 + x ^ 3 + x ^ 2 + x = x * (x * (x * 1) + 1) + 1) जैसे अनुकूलन भी लागू नहीं होते हैं।

var t = a ^ 2; a * a * a * a * a a = t ^ 2 * t - सामान्य "तेज" एल्गोरिथ्म।
एक * a * a * a * a = a (a ^ 3) ^ 2 - इष्टतम "तेज" एल्गोरिथ्म।

वैसे, यह उल्लेख के लायक है कि सामान्य निश्चित संख्या के लिए डबल, उपरोक्त गुणन के लिए एक अलग क्रम में गुणा करने का परिणाम अलग होगा (यानी (ए ^ 2) ^ 2 * ए ^ 2! = (ए ^ 3) ^ 2! )। और इस वजह से, कुछ संकलक इनमें से कई अभिव्यक्तियों का अनुकूलन नहीं करते हैं। इस बारे में स्टैकओवरलॉफ़ में दिलचस्प क्यू एंड ए हैं: जीसीसी एक ए * ए * ए * ए * टू (ए * ए * ए) * (ए * ए * ए) का अनुकूलन क्यों नहीं करता है? और क्यों Math.Pow (x, 2) x * x न तो संकलक और न ही JIT के लिए अनुकूलित है? ।

स्थानीय चर अनुकूलन

जैसा कि पिछले चरणों से ज्ञात है, स्थानीय चर का उपयोग उन सभी कार्यों के परिणाम को संग्रहीत करने के लिए किया जाता है जो मूल अभिव्यक्ति में 1 से अधिक बार होते हैं। स्थानीय चर के साथ काम करने के लिए, केवल दो सरल निर्देशों का उपयोग किया जाता है: स्टालोक और एलडलोक , जो एक तर्क का उपयोग करते हैं, जो इस स्थानीय चर की संख्या के लिए जिम्मेदार है। लेकिन अगर हर बार दोहराया गणना परिणाम (इसे बनाने के लिए) में एक स्थानीय चर की संख्या बढ़ाई जाती है, तो बहुत सारे स्थानीय चर हो सकते हैं। इस समस्या को कम करने के लिए, स्थानीय चर के जीवन चक्र को संपीड़ित करने के लिए एक एल्गोरिथ्म लागू किया गया था, जिसकी प्रक्रिया को नीचे की आकृति में स्पष्ट रूप से देखा जा सकता है। जैसा कि आप देख सकते हैं, अभिव्यक्ति में 5 स्थानीय चर के बजाय, आप केवल 3 का उपयोग कर सकते हैं। हालांकि, यह "लालची" एल्गोरिथ्म सबसे इष्टतम क्रमचय नहीं है, हालांकि, यह कार्य कार्यान्वित होने के लिए काफी उपयुक्त है।

अपरिभाषित कार्यों और उनके डेरिवेटिव का संकलन

विकसित पुस्तकालय में, आप न केवल फॉर्म f (x) के एक चर के सरल कार्यों का उपयोग कर सकते हैं, बल्कि अन्य भी, जैसे कि f (x, a, b (x)), जहां एक अज्ञात स्थिरांक है और b (x) एक अज्ञात कार्य है एक प्रतिनिधि के रूप में प्रेषित। जैसा कि आप जानते हैं, किसी भी फ़ंक्शन के व्युत्पन्न की परिभाषा इस प्रकार है: b (x) '= (b (x + dx) - b (x)) / dx। और जब संकलन मॉड्यूल एक अपरिभाषित फ़ंक्शन का सामना करता है, तो यह निम्नलिखित कोड उत्पन्न करता है:

 ldarg.1 ldarg.0 callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) ret

अनिश्चित समारोह के व्युत्पन्न की गणना के लिए कोड (dx = 0.000001)

 ldarg.1 ldarg.0 ldc.r8 1E-06 add callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) ldarg.1 ldarg.0 callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) sub ldc.r8 0.000001 div ret

व्युत्पन्न की संख्यात्मक गणना के लिए, आप अन्य, अधिक सटीक तरीकों का उपयोग कर सकते हैं ।

परीक्षण

परीक्षण प्रसंस्करण के कई चरणों के लिए आयोजित किया गया था, जिसे MathFunction.Tests परियोजना में देखा जा सकता है। दिलचस्प बिंदुओं में से, एक विश्लेषणात्मक डेरिवेटिव का परीक्षण करने और डोमेन का उपयोग करके असेंबलियों को लोड करने और अनलोड करने के लिए वुल्फ्रेमएल्फा.नेट के उपयोग का उल्लेख कर सकता है ।

वॉलफ्रेम अल्फा

WolframAlpha.NET प्रसिद्ध गणित सेवा wolframalpha के लिए एक एपीआई आवरण है । मेरी परियोजना में, मेरे पुस्तकालय का उपयोग करके प्राप्त व्युत्पन्न के साथ इस सेवा पर प्राप्त स्पष्ट रूप से सही व्युत्पन्न की तुलना करने के लिए यह काम में आया। निम्नानुसार उपयोग किया जाता है:

 public static bool CheckDerivative(string expression, string derivative) { return CheckEquality("diff(" + expression + ")", derivative); } public static bool CheckEquality(string expression1, string expression2) { WolframAlpha wolfram = new WolframAlpha(ConfigurationManager.AppSettings["WolframAlphaAppId"]); string query = "(" + expression1.Replace(" ", "") + ")-(" + expression2.Replace(" ", "") + ")"; QueryResult result = wolfram.Query(query); result.RecalculateResults(); try { double d; return double.TryParse(result.GetPrimaryPod().SubPods[0].Plaintext, out d) && d == 0.0; } catch { return false; } }

डोमेन का उपयोग करके असेंबली डाउनलोड और अपलोड करें

एक डोमेन बनाना, एक फ़ाइल से असेंबल करना, एक निश्चित प्रकार का उदाहरण बनाना और तरीकों के बारे में जानकारी के साथ ऑब्जेक्ट प्राप्त करना (MethodInfo):

 Domain = AppDomain.CreateDomain("MathFuncDomain"); MathFuncObj = _domain.CreateInstanceFromAndUnwrap(FileName, NamespaceName + "." + ClassName); Type mathFuncObjType = _mathFuncObj.GetType(); Func = mathFuncObjType.GetMethod(FuncName); FuncDerivative = mathFuncObjType.GetMethod(FuncDerivativeName);

संकलित फ़ंक्शन के परिणाम की गणना:

 return (double)Func.Invoke(_mathFuncObj, new object[] { x })

डोमेन को लोड करना और असेंबली फ़ाइल को हटाना:

 if (_domain != null) AppDomain.Unload(Domain); File.Delete(FileName);

उत्पन्न आईएल कोड की तुलना

अंतिम IL कोड रिलीज़ मोड में मानक C # संकलक csc.exe द्वारा उत्पन्न कोड की तुलना में अधिक इष्टतम है, बस फ़ंक्शन के लिए, निम्न दो सूचियों की तुलना देखें

 x ^ 3 + sin(3 * ln(x * 1)) + x ^ ln(2 * sin(3 * ln(x))) - 2 * x ^ 3

csc.exe .NET 4.5.1 MathExpressions.NET

 IL_0000: ldarg.0 IL_0001: ldarg.0 IL_0002: mul IL_0003: ldarg.0 IL_0004: mul IL_0005: ldc.r8 3 IL_000e: ldarg.0 IL_000f: ldc.r8 1 IL_0018: mul IL_0019: call float64 [mscorlib]System.Math::Log(float64) IL_001e: mul IL_001f: call float64 [mscorlib]System.Math::Sin(float64) IL_0024: add IL_0025: ldarg.0 IL_0026: ldc.r8 2 IL_002f: ldc.r8 3 IL_0038: ldarg.0 IL_0039: call float64 [mscorlib]System.Math::Log(float64) IL_003e: mul IL_003f: call float64 [mscorlib]System.Math::Sin(float64) IL_0044: mul IL_0045: call float64 [mscorlib]System.Math::Log(float64) IL_004a: call float64 [mscorlib]System.Math::Pow(float64, float64) IL_004f: add IL_0050: ldc.r8 2 IL_0059: ldarg.0 IL_005a: mul IL_005b: ldarg.0 IL_005c: mul IL_005d: ldarg.0 IL_005e: mul IL_005f: sub IL_0060: ret

 IL_0000: ldc.r8 3 IL_0009: ldarg.0 IL_000a: call float64 [mscorlib]System.Math::Log(float64) IL_000f: mul IL_0010: call float64 [mscorlib]System.Math::Sin(float64) IL_0015: stloc.0 IL_0016: ldloc.0 IL_0017: ldarg.0 IL_0018: ldarg.0 IL_0019: mul IL_001a: ldarg.0 IL_001b: mul IL_001c: sub IL_001d: ldarg.0 IL_001e: ldc.r8 2 IL_0027: ldloc.0 IL_0028: mul IL_0029: call float64 [mscorlib]System.Math::Log(float64) IL_002e: call float64 [mscorlib]System.Math::Pow(float64, float64) IL_0033: add IL_0034: ret

इसी समय, यह देखना दिलचस्प है कि यह कैसे ILSpy में एक सी फ़ंक्शन के लिए असंतुष्ट सी # कोड का परिणाम देता है जो उपरोक्त फ़ंक्शन का व्युत्पन्न है, अर्थात्। को

 (ln(2 * sin(3 * ln(x))) * x ^ -1 + 3 * ln(x) * cos(3 * ln(x)) * sin(3 * ln(x)) ^ -1 * x ^ -1) * x ^ ln(2 * sin(3 * ln(x))) + 3 * cos(3 * ln(x)) * x ^ -1 + -(3 * x ^ 2)

 double arg_24_0 = 2.0; double arg_1A_0 = 3.0; double num = Math.Log(x); double num2 = arg_1A_0 * num; double num3 = Math.Sin(num2); double num4 = Math.Log(arg_24_0 * num3); double arg_3B_0 = num4; double num5 = 1.0 / x; double arg_54_0 = arg_3B_0 * num5; double arg_4F_0 = 3.0 * num; num = Math.Cos(num2); return (arg_54_0 + arg_4F_0 * num / num3 * num5) * Math.Pow(x, num4) + num * num5 * 3.0 - x * x * 3.0;

जैसा कि आप देख सकते हैं, पहले से गणना किए गए फ़ंक्शन परिणामों को संग्रहीत करने के लिए बड़ी संख्या में स्थानीय चर बनाए गए हैं। हालांकि वास्तविकता में कम स्थानीय चर हैं, क्योंकि, उदाहरण के लिए, डबल arg_24_0 = 2.0 के लिए; एक स्थानीय चर नहीं बनाया गया है, यह सिर्फ एक स्थिर है।

बेशक, वास्तविक अनुप्रयोगों में ऐसे भाव बहुत कम पाए जाते हैं, लेकिन, फिर भी, वर्णित अनुकूलन का उपयोग अन्य, अधिक लागू मामलों में और संकलक की बेहतर समझ के लिए किया जा सकता है।

निष्कर्ष

उपरोक्त सभी को C # में लागू करने के दौरान, मैंने महसूस किया कि एक कार्यात्मक भाषा उन कार्यों के लिए अधिक उपयुक्त है जहाँ आपको प्रतीकात्मक गणना और प्रतिस्थापन से संबंधित कुछ करने की आवश्यकता है। यहां तक कि, उदाहरण के लिए, ओपनसोर्स मैक्सिमा कंप्यूटर बीजगणित प्रणाली लिस्प में लिखी गई है। वैसे, एफ # पर कोडप्रोजेक्ट पर प्रतीकात्मक गणनाओं का कार्यान्वयन है , और मेरी परियोजना की तुलना में वहां स्पष्ट रूप से कम कोड है। हालांकि, इस परियोजना के कार्यान्वयन ने मुझे पार्सिंग अभिव्यक्तियों में अधिक अनुभव प्राप्त करने, अनुकूलन करने, निम्न-स्तरीय कोड उत्पन्न करने, फ़्लोटिंग-पॉइंट नंबरों के साथ काम करने और बस गणित में अनुमति दी।

सभी रुचि के लिए, मैंने इसे गीथूब: स्रोत पर पोस्ट किया । कार्यक्रम स्वयं भी उपलब्ध है: MathExpressions.NET। तत्काल जरूरत के मामले में मैं इसे रिफ्लेक्टर कर सकता हूं। पुल अनुरोधों का स्वागत है।

PS। एक लंबा सूत्र दिल में छिपा है, जिसमें शब्दों, कारकों और सरलीकरण की व्यवस्था को ध्यान में रखा गया है। इसकी जटिलता के दौरान, विकसित कार्यक्रम का उपयोग किया गया था।

अद्यतन: चूंकि किसी ने अनुमान नहीं लगाया कि दिल में क्या एन्क्रिप्ट किया गया है, इसलिए मैं परिणाम पोस्ट करता हूं। यह सूत्र Matiyasevich बहुपद का एक विशेष मामला है , जिसके सकारात्मक मानों का सेट गैर-नकारात्मक मानों के लिए primes के सेट से मेल खाता है। विकिपीडिया में भी जानकारी है ।

.NET में गणितीय अभिव्यक्तियाँ (पार्सिंग, विभेदन, सरलीकरण, अंश, संकलन)