सहयोगात्मक फ़िल्टरिंग

आधुनिक दुनिया में, अक्सर एक सूचना प्रणाली के उपयोगकर्ताओं को सामान या सेवाओं की सिफारिश करने की समस्या का सामना करना पड़ता है। पुराने दिनों में, सबसे लोकप्रिय उत्पादों के सारांश के साथ सिफारिशें की गई थीं: यह अब भी उसी Google Play को खोलकर देखा जा सकता है। लेकिन समय के साथ, इस तरह की सिफारिशों को लक्षित (लक्षित) ऑफ़र द्वारा अधिगृहीत किया जाने लगा: उपयोगकर्ताओं को न केवल लोकप्रिय उत्पादों की सिफारिश की जाती है, बल्कि वे उत्पाद जो उन्हें निश्चित रूप से पसंद आएंगे। इतनी देर पहले, नेटफ्लिक्स ने $ 1 मिलियन के पुरस्कार पूल के साथ एक प्रतियोगिता आयोजित की, जिसका काम फिल्मों की सिफारिश करने के लिए एल्गोरिथ्म में सुधार करना था ( अधिक )। इसी तरह के एल्गोरिदम कैसे काम करते हैं?

यह लेख उपयोगकर्ता समानता के लिए सहयोगी फ़िल्टरिंग एल्गोरिदम पर चर्चा करता है, जिसे कॉशन माप का उपयोग करके निर्धारित किया गया है, साथ ही अजगर में इसका कार्यान्वयन भी किया गया है।

इनपुट डेटा

मान लें कि हमारे पास उन रेटिंग्स का एक मैट्रिक्स है जो उपयोगकर्ता उत्पादों के लिए प्रस्तुत करते हैं, प्रस्तुति की सादगी के लिए, उत्पादों को 1-9 नंबर दिए जाते हैं:


आप इसे एक सीएसवी फ़ाइल का उपयोग करके निर्दिष्ट कर सकते हैं जिसमें पहला कॉलम उपयोगकर्ता नाम है, दूसरा उत्पाद पहचानकर्ता है, और तीसरा उपयोगकर्ता की रेटिंग है। इस प्रकार, हमें निम्नलिखित सामग्रियों के साथ एक सीएसवी फ़ाइल की आवश्यकता है:

alex,1,5.0 alex,2,3.0 alex,5,4.0 ivan,1,4.0 ivan,6,1.0 ivan,8,2.0 ivan,9,3.0 bob,2,5.0 bob,3,5.0 david,3,4.0 david,4,3.0 david,6,2.0 david,7,1.0 

शुरू करने के लिए, हम एक फ़ंक्शन विकसित करेंगे जो उपरोक्त सीएसवी फ़ाइल को पढ़ता है। सिफारिशों को संग्रहीत करने के लिए, हम अजगर के लिए मानक ताना डेटा संरचना का उपयोग करेंगे: प्रत्येक उपयोगकर्ता को "उत्पाद": "रेटिंग" फॉर्म की अपनी रेटिंग की एक निर्देशिका सौंपी जाती है। निम्नलिखित कोड निकलेगा:

 import csv def ReadFile (filename = "<csv_file_location>"): f = open (filename) r = csv.reader (f) mentions = dict() for line in r: user = line[0] product = line[1] rate = float(line[2]) if not user in mentions: mentions[user] = dict() mentions[user][product] = rate f.close() return mentions 

समानता का माप

यह स्पष्ट रूप से स्पष्ट है कि उपयोगकर्ता नंबर 1 के लिए एक उत्पाद की सिफारिश करने के लिए, आपको उन उत्पादों से चुनने की आवश्यकता है जो कुछ 2-3-4-आदि। उपयोगकर्ता पसंद करते हैं, जो उपयोगकर्ता संख्या 1 में उनकी रेटिंग के समान हैं। उपयोगकर्ताओं की इस "समानता" की एक संख्यात्मक अभिव्यक्ति कैसे प्राप्त करें? मान लीजिए कि हमारे पास M उत्पाद हैं। व्यक्तिगत उपयोगकर्ता द्वारा निर्धारित की गई रेटिंग उत्पादों के एम-आयामी स्थान में एक वेक्टर है, और हम वैक्टर की तुलना कर सकते हैं। संभावित उपायों में निम्नलिखित हैं:

1. कोसाइन माप
2. पीयरसन सहसंबंध गुणांक
3. यूक्लिडियन दूरी
4. तनिमोटो गुणांक
5. मैनहट्टन दूरी, आदि।

अधिक विस्तार से, उनके आवेदन के विभिन्न उपायों और पहलुओं, मैं एक अलग लेख में विचार करने जा रहा हूं। अभी के लिए, यह कहने के लिए पर्याप्त है कि सिफारिशकर्ता प्रणालियों में कोसाइन माप और तनीमोतो के सहसंबंध गुणांक सबसे अधिक बार उपयोग किए जाते हैं। आइए हम कोसाइन उपाय पर अधिक विस्तार से विचार करें, जिसे हम लागू करने जा रहे हैं। दो वैक्टर के लिए कोसाइन माप उनके बीच के कोण का कोसाइन है। गणित में स्कूल के पाठ्यक्रम से, हमें याद है कि दो वैक्टरों के बीच का कोसाइन उनका स्केलर उत्पाद है जो प्रत्येक दो वैक्टरों की लंबाई से विभाजित होता है:

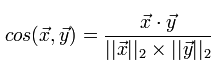
हम इस माप की गणना को कार्यान्वित करते हैं, यह नहीं भूलते कि हमारे पास कई उपयोगकर्ता रेटिंग हैं जो प्रपत्र "उत्पाद" में प्रस्तुत की गई हैं: "रेटिंग"

 def distCosine (vecA, vecB): def dotProduct (vecA, vecB): d = 0.0 for dim in vecA: if dim in vecB: d += vecA[dim]*vecB[dim] return d return dotProduct (vecA,vecB) / math.sqrt(dotProduct(vecA,vecA)) / math.sqrt(dotProduct(vecB,vecB)) 

कार्यान्वयन के दौरान, इस तथ्य का उपयोग किया गया था कि वेक्टर का स्केलर उत्पाद स्वयं वेक्टर की लंबाई का वर्ग देता है - यह प्रदर्शन के दृष्टिकोण से सबसे अच्छा समाधान नहीं है, लेकिन हमारे उदाहरण में गति मौलिक नहीं है।

सहयोगात्मक फ़िल्टरिंग एल्गोरिथ्म

इसलिए, हमारे पास उपयोगकर्ता प्राथमिकताओं का एक मैट्रिक्स है और हम यह निर्धारित करने में सक्षम हैं कि दो उपयोगकर्ता एक दूसरे के समान कैसे हैं। अब यह सहयोगी फ़िल्टरिंग एल्गोरिदम को लागू करने के लिए बना हुआ है, जिसमें निम्नलिखित शामिल हैं:

1. L उपयोगकर्ताओं का चयन करें, जिनका स्वाद प्रश्न के स्वाद के समान है। ऐसा करने के लिए, प्रत्येक उपयोगकर्ता के लिए, प्रश्न में उपयोगकर्ता के संबंध में चयनित माप (हमारे मामले में, कोसाइन) की गणना करना आवश्यक है, और एल सबसे बड़े का चयन करें। इवान के लिए, उपरोक्त तालिका से, हमें निम्नलिखित मूल्य मिलते हैं:
   
2. प्रत्येक उपयोगकर्ता के लिए, परिकलित माप मान द्वारा उसकी रेटिंग को गुणा करें, इसलिए अधिक "समान" उपयोगकर्ताओं की रेटिंग से उत्पाद की अंतिम स्थिति पर अधिक प्रभाव पड़ेगा, जिसे नीचे दी गई व्याख्या में तालिका में देखा जा सकता है।
3. प्रत्येक उत्पाद के लिए, निकटतम उपयोगकर्ताओं के L के कैलिब्रेटेड अनुमानों की राशि की गणना करें, चयनित उपयोगकर्ताओं के उपायों L के योग से परिणामी राशि को विभाजित करें। राशि को स्ट्रिंग "योग" में चित्रण में दिखाया गया है, स्ट्रिंग में कुल मूल्य "परिणाम"
   
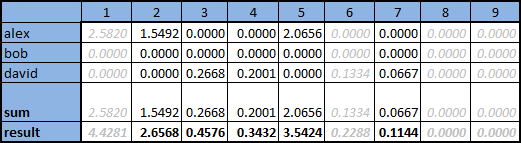
   उन उत्पादों के कॉलम जो पहले से ही उपयोगकर्ता द्वारा प्रश्न में दिए गए हैं, उन्हें ग्रे में चिह्नित किया गया है और उन्हें उन्हें फिर से पेश करने का कोई मतलब नहीं है

सूत्र के रूप में, इस एल्गोरिथ्म का प्रतिनिधित्व किया जा सकता है

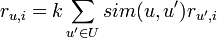
जहां सिम फ़ंक्शन उन दो उपयोगकर्ताओं की समानता का माप है, जिन्हें हमने चुना है, यू उपयोगकर्ताओं का सेट है, आर को असाइन किया गया ग्रेड है, कश्मीर सामान्यीकरण गुणांक है:


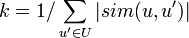
अब यह केवल उपयुक्त कोड लिखने के लिए रह गया है

 import math def makeRecommendation (userID, userRates, nBestUsers, nBestProducts): matches = [(u, distCosine(userRates[userID], userRates[u])) for u in userRates if u <> userID] bestMatches = sorted(matches, key=lambda(x,y):(y,x), reverse=True)[:nBestUsers] print "Most correlated with '%s' users:" % userID for line in bestMatches: print " UserID: %6s Coeff: %6.4f" % (line[0], line[1]) sim = dict() sim_all = sum([x[1] for x in bestMatches]) bestMatches = dict([x for x in bestMatches if x[1] > 0.0]) for relatedUser in bestMatches: for product in userRates[relatedUser]: if not product in userRates[userID]: if not product in sim: sim[product] = 0.0 sim[product] += userRates[relatedUser][product] * bestMatches[relatedUser] for product in sim: sim[product] /= sim_all bestProducts = sorted(sim.iteritems(), key=lambda(x,y):(y,x), reverse=True)[:nBestProducts] print "Most correlated products:" for prodInfo in bestProducts: print " ProductID: %6s CorrelationCoeff: %6.4f" % (prodInfo[0], prodInfo[1]) return [(x[0], x[1]) for x in bestProducts] 

इसके स्वास्थ्य की जांच करने के लिए, आप निम्नलिखित कमांड चला सकते हैं:

 rec = makeRecommendation ('ivan', ReadFile(), 5, 5) 

जिसके परिणामस्वरूप निम्न परिणाम होंगे:

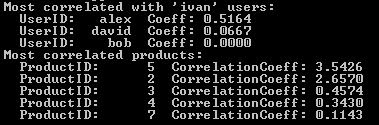
निष्कर्ष

हमने एक उदाहरण देखा और एक कोसाइनिटी ​​समानता माप का उपयोग करके सहयोगी फ़िल्टरिंग के लिए सबसे सरल विकल्पों में से एक को लागू किया। यह समझना महत्वपूर्ण है कि सहयोगी फ़िल्टरिंग के अन्य दृष्टिकोण हैं, उत्पाद रेटिंग की गणना के लिए अन्य सूत्र , समानता के अन्य उपाय ( लेख , अनुभाग "यह भी देखें")। इस विचार का और विकास निम्नलिखित क्षेत्रों में किया जा सकता है:

1. प्रयुक्त डेटा संरचनाओं का अनुकूलन । जब पायथन में डेटा को एक तानाशाह के रूप में संग्रहीत किया जाता है, तो हर बार एक विशेष मूल्य तक पहुँचा जाता है, एक हैश की गणना की जाती है और स्थिति बदतर हो जाती है नाम स्ट्रिंग। व्यावहारिक कार्यों में, डेटा को संग्रहीत करने के लिए विरल मैट्रिस का उपयोग किया जा सकता है, और पाठ उपयोगकर्ता नाम और उत्पाद नाम के बजाय संख्यात्मक पहचानकर्ताओं (सभी उपयोगकर्ताओं और सभी उत्पादों की संख्या) का उपयोग किया जा सकता है
2. प्रदर्शन अनुकूलन । जाहिर है, प्रत्येक उपयोगकर्ता संपर्क के लिए सिफारिश की गणना करना बेहद महंगा है। इस समस्या के लिए कई समाधान हैं:
   
   • उपयोगकर्ताओं को क्लस्टर करना और समान क्लस्टर से संबंधित उपयोगकर्ताओं के बीच समानता के उपायों की गणना करना
   • उत्पाद-उत्पाद समानता कारकों की गणना। ऐसा करने के लिए, आपको उपयोग-उत्पाद मैट्रिक्स (आपको उत्पाद-उपयोगकर्ता मैट्रिक्स प्राप्त होता है) को स्थानांतरित करने की आवश्यकता होती है, जिसके बाद प्रत्येक उत्पादों के लिए समान कोसाइन माप का उपयोग करते हुए और के करीबी लोगों को याद करते हुए सबसे समान उत्पादों के सेट की गणना करते हैं। यह एक समय लेने वाली प्रक्रिया है, इसलिए इसे हर M घंटे / दिन में एक बार किया जा सकता है। लेकिन अब हमारे पास इसके समान उत्पादों की एक सूची है, और उत्पाद की समानता के माप के मूल्य से उपयोगकर्ता रेटिंग को गुणा करते हुए, हमें O (N * k) के लिए एक अनुशंसा मिलती है, जहां N उपयोगकर्ता रेटिंग की संख्या है
3. समानता के उपायों का चयन । कोसाइन माप सबसे अधिक इस्तेमाल किया जाता है, लेकिन सिस्टम डेटा के विश्लेषण के परिणामों के अनुसार ही माप का चयन किया जाना चाहिए
4. फ़िल्टरिंग एल्गोरिथ्म का संशोधन । शायद एक और फ़िल्टरिंग एल्गोरिथ्म एक विशेष प्रणाली में अधिक सटीक सिफारिशें देगा। फिर से, विभिन्न एल्गोरिदम की तुलना केवल तभी की जा सकती है जब किसी विशिष्ट सिस्टम पर लागू किया जाता है।

साहित्य

1. हम सामूहिक मन का कार्यक्रम करते हैं
2. सहयोगात्मक विकी फ़िल्टरिंग
3. कोसाइन उपाय
4. विरल Matrices