गॉसियन क्विक ब्लर

गॉसियन ब्लर फ़िल्टर (फ़ोटोशॉप में व्यापक रूप से ज्ञात "गॉसियन ब्लर") का उपयोग अक्सर अपने स्वयं के या अन्य छवि प्रसंस्करण एल्गोरिदम के हिस्से के रूप में किया जाता है। इसके बाद, एक विधि का वर्णन किया जाएगा जो एक अनंत आवेग प्रतिक्रिया के साथ फिल्टर का उपयोग करके धब्बा त्रिज्या से स्वतंत्र गति से धुंधला होने की अनुमति देता है।

विधि का वर्णन अंग्रेजी में है । लेकिन रूसी में कोई जानकारी नहीं है। इसके अलावा, मैंने कुछ बदलाव किए हैं।

तो, मूल छवि को चमक x ( m, n ) द्वारा दिया जाए। एक त्रिज्या आर के साथ गाऊसी धब्बा की गणना सूत्र द्वारा की जाती है



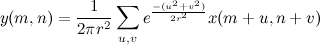यू और वी पर योग सीमा को कई सिग्मा के साथ प्लस या माइनस के रूप में चुना जा सकता है, अर्थात्। त्रिज्या r , जो O ( r ² ) संचालन के क्रम के एल्गोरिदम की जटिलता को प्रति पिक्सेल देता है। बड़े आर और बहु-मेगापिक्सेल छवियों के लिए, बहुत अच्छा नहीं है, है ना?

पहला त्वरण गाऊसी धब्बा की पृथक्करण गुण देता है। यही है, आप प्रत्येक पंक्ति के लिए x अक्ष के साथ फ़िल्टर कर सकते हैं, प्रत्येक कॉलम के लिए y द्वारा परिणामी छवि को फ़िल्टर कर सकते हैं और प्रति पिक्सेल O ( r ) संचालन की जटिलता के साथ एक ही परिणाम प्राप्त कर सकते हैं। पहले से बेहतर है। हम इस संपत्ति का उपयोग भी करेंगे, इसलिए, आगे के सभी तर्क एक-आयामी मामले के लिए होंगे, जहां x ( n ) होने के लिए y ( n ) प्राप्त करना आवश्यक है।

एक असीम आवेग प्रतिक्रिया के साथ फ़िल्टर हमें इसके साथ मदद करेंगे। फ़िल्टर का विचार यह है: y ( n ) के मानों की पुनरावृत्ति सूत्र द्वारा गणना की जाती है:



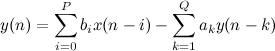
जहां एक और बी _i कुछ गणना गुणांक हैं, और y ( n ) और x ( n ) के लिए n <0 शून्य माना जाता है।

B _{i के} आधार पर सूत्र का हिस्सा एक परिमित कर्नेल के साथ एक सरल दृढ़ संकल्प तक कम हो जाता है। चूँकि हम चाहते हैं कि फ़िल्टर को और तेज़ माना जाए, हम अपने फ़िल्टर को P = 0 के लिए खोजेंगे, अर्थात् एक गुणांक b _{0 पर} विचार करेंगे।

बस मामले में, मैं आपको याद दिलाता हूं कि किसी भी रैखिक फिल्टर (और IIR फ़िल्टर भी रैखिक है) पूरी तरह से डेल्टा फ़ंक्शन के लिए अपनी प्रतिक्रिया की विशेषता है, बिंदु 0 पर 1 के बराबर है, और अन्य सभी बिंदुओं पर 0 है। वह हिस्सा जो गुणांक पर निर्भर करता है जब इस तरह के एक फ़ंक्शन का जवाब देना या तो विचलन करेगा और अनंत तक जाएगा (मैं इससे बचना चाहूंगा), या यह हमें एक सुंदर वानिंग पूंछ देगा। उदाहरण के लिए, इस तरह:



एक गॉस की तरह लगता है? ठीक है, हाँ, कुछ पहले से मौजूद है, लेकिन किसी तरह यह अजीब लग रहा है। इसलिए, एल्गोरिथ्म का विचार यह होगा: हम एक ही दिशा में (एक _{अधिकतम} गुणांक से), और फिर विपरीत दिशा ( n _{अधिकतम} 0 से) में परिणाम को एक दिशा में फ़िल्टर करेंगे। गणितीय रूप से, एक कड़ाई से सममित वक्र प्राप्त किया जाना चाहिए (इसलिए, यदि आप पहले और आगे, या इसके विपरीत फ़िल्टर करते हैं तो यह कोई मायने नहीं रखता है)। थोड़ा आगे दौड़ने पर, यही होता है अगर आप इसे रिवर्स ऑर्डर में फ़िल्टर करते हैं:



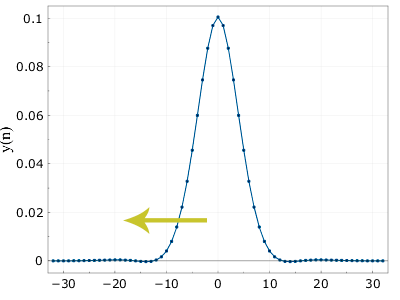
यहाँ। लगभग हमें जो चाहिए। लगभग, क्योंकि वास्तव में, बिल्कुल नहीं। वक्र थोड़ा नकारात्मक क्षेत्र में चला जाता है, और सामान्य तौर पर सटीक गाऊसी से भिन्न होता है। लेकिन अधिकांश अनुप्रयोगों के लिए, यह सब काफी स्वीकार्य है, इसके अतिरिक्त, यदि आपको इसे सुनिश्चित करने के लिए बिल्कुल विचार करने की आवश्यकता है, तो आप क्यू फिल्टर के क्रम को बढ़ा सकते हैं।

तो, यह फिल्टर गुणांक की गणना करने के लिए बनी हुई है a । इसके अलावा, सभी सूत्र Q = 3 केस के लिए जाएंगे।

सामान्य तौर पर, तथाकथित ट्रांसफर फ़ंक्शन का उपयोग करके फ़िल्टर का अध्ययन किया जाता है । जो लोग चाहते हैं वे पढ़ सकते हैं कि यह सब क्या है, और शुरुआत के लिए यह हमारे लिए पर्याप्त है कि यह अभी मौजूद है और इसमें कुछ गुण हैं। एक रैखिक फिल्टर के लिए इस फ़ंक्शन का सामान्य दृश्य निम्नानुसार होगा:



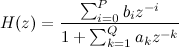
या हमारे मामले के लिए, क्यू = 3, पी = 1:



चूंकि अंश और हर में बहुपद होते हैं, उन्हें कारक बनाया जा सकता है। अंश, सामान्य मामले में, हमें शून्य देगा (हमारे मामले में शून्य नहीं हैं), और भाजक डंडे देगा:



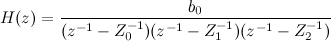
हमारे मामले में, 1 / जेड ₀ , 1 / जेड ₁ , 1 / जेड ₂ । ध्यान दें कि ध्रुव विशिष्ट रूप से गुणांक _को हमारे फ़िल्टर के _k निर्धारित करते हैं (सभी IIR फ़िल्टर आमतौर पर डंडे के माध्यम से खोजे जाते हैं, और सीधे नहीं)। वैसे, ध्रुवों पर गुणांक प्राप्त करना इसके विपरीत से आसान है (इसके लिए आपको बहुपदों को गुणा करना होगा, और इसके विपरीत - बिजली समीकरण को हल करना)।

सबसे महत्वपूर्ण सैद्धांतिक आसन जो हमारे लिए उपयोगी है: यदि जटिल ध्रुव इकाई सर्कल के अंदर स्थित है, अर्थात। modulo एक से भी कम, (या, जो कि एक ही चीज है, Z ₀ , Z ₁ , Z ₂ यूनिट यूनिट के बाहर का व्युत्क्रम मान), फिर फ़िल्टर स्थिर होगा, फिर परिणाम अनन्तता तक नहीं आएगा।

हम यह भी ध्यान देते हैं कि मनमाने ढंग से जटिल संयुग्मों का नामकरण करके Z ₀ , Z ₁ और वास्तविक Z ₂ (फिर से, सब कुछ एक से अधिक मोडुलो है), हम उनसे एक फिल्टर का निर्माण कर सकते हैं। उत्पाद में, सब कुछ सख्ती से वास्तविक गुणांक में बदल जाता है a ।

गुणांक b ₀ फ़िल्टर के "वॉल्यूम फैक्टर" के रूप में कार्य करता है।

तो, समस्या तीन गुणांक Z ₀ , Z ₁ , Z ₂ के निर्धारण में कम हो गई थी। चूंकि, मैं दोहराता हूं, उनमें से दो जटिल संयुग्म हैं, और तीसरा वास्तविक है, आपको पहले के वास्तविक और काल्पनिक भागों और तीसरे के वास्तविक को खोजने की आवश्यकता है। अर्थात्, तीन वास्तविक संख्याएँ: वास्तविक ( Z ₀ ), im ( Z ₀ ), Z ₂

इन तीन नंबरों को हमारे द्वारा आवश्यक फिल्टर त्रिज्या के संदर्भ में व्यक्त किया जाना चाहिए। ध्यान दें कि वास्तव में यह दो से अधिक या बराबर आर के लिए विचार करने के लिए समझ में आता है, छोटे मूल्यों के साथ गुणा से फ़िल्टर करना तेज होता है।

इसके अलावा मैं "पुनरावर्ती गाऊसी व्युत्पन्न फिल्टर" की तुलना में थोड़ा अलग तरीके से चला गया। वहां उन्होंने मामले को r = 2 के साथ अन्य सभी के लिए बढ़ा दिया, और मैंने 2 से 2048 तक के सभी गुणांक को एक घातीय कदम के साथ निर्धारित किया। मैंने एक अनुकूलन एल्गोरिथ्म लिखा है जो अधिकतम अंतर मापांक को कम करके निकटतम वक्र की खोज करता है। एक अतिरिक्त स्थिति पूर्ण ऊर्जा के फिल्टर द्वारा संरक्षण थी, अर्थात। ताकि फंक्शन x ( n ) = कॉन्स्टेंट अपने आप में गुजर जाए, जो स्थिति देता है

बी ₀ = 1- ( एक ₁ + ₂ + ₃ )

मैंने विभिन्न अनुकूलन एल्गोरिदम की कोशिश की, और सबसे अच्छे लोगों ने थोड़ा संशोधित आनुवंशिक एल्गोरिथ्म दिखाया। (शायद, आप अनुकूलन के बारे में एक अलग नोट लिख सकते हैं)।

इच्छुक लोग Google स्प्रेडशीट पर परिणाम देख सकते हैं।

यह देखा जा सकता है कि केस आर = 2 के लिए, परिणाम कार्य में डेटा से भिन्न होते हैं। ऐसा क्यों है, मैं नहीं कह सकता, एक ही समय में, मेरी गणना के अनुसार, मेरे गुणांक 40 प्रतिशत, त्रुटि से एक छोटे से देते हैं।

इसके अलावा, मैंने पत्र का उपयोग नहीं किया लेकिन लेख की भावना, और डेटा के रूप में खोजना शुरू किया

real ( Z ₀ ) = cos ( W ( r ) / r ) * e ^{A ( r ) / r}
im ( Z ₀ ) = sin ( W ( r ) / r ) * e ^{A ( r ) / r}
जेड ₂ = ई ^{बी ( आर ) / आर}

यानी फिर आपको बस तीन समान कार्य करने होंगे, जिनमें से प्रत्येक एक स्थिर सीमा में जाता है। मैं रिलेशन के रूप में एक फंक्शन की तलाश में था

( k ₃ r ³ + k ₂ r ² + k ₁ r + k ₀ ) / r ³

और गुणांक को सरलतम तरीके से उठाया - सिर्फ वोल्फ्राम मैथेमेटिका का उपयोग करके। वैसे, यदि आप तालिकाओं से डेटा के ग्राफ़ का सावधानीपूर्वक अध्ययन करते हैं, तो आप देख सकते हैं कि फ़ंक्शन में कुछ हद तक आरी है। इसलिए, जब अनुमान लगाते हैं, तो हम सटीकता में थोड़ा कम हो जाते हैं, लेकिन वास्तव में थोड़ा सा - तालिका से मान पोलिनोमियल द्वारा प्राप्त की तुलना में 10 प्रतिशत छोटे त्रुटि देगा।

खैर यहाँ। उन लोगों के लिए जो पहले से ही भ्रमित हैं कि क्या और क्या विचार करने की आवश्यकता है, मैं गुणांक की गणना के लिए अंतिम फ़ंक्शन कोड सी में दूंगा:

int gaussCoef(double sigma, double a[3], double *b0) { double sigma_inv_4; sigma_inv_4 = sigma*sigma; sigma_inv_4 = 1.0/(sigma_inv_4*sigma_inv_4); double coef_A = sigma_inv_4*(sigma*(sigma*(sigma*1.1442707+0.0130625)-0.7500910)+0.2546730); double coef_W = sigma_inv_4*(sigma*(sigma*(sigma*1.3642870+0.0088755)-0.3255340)+0.3016210); double coef_B = sigma_inv_4*(sigma*(sigma*(sigma*1.2397166-0.0001644)-0.6363580)-0.0536068); double z0_abs = exp(coef_A); double z0_real = z0_abs*cos(coef_W); double z0_im = z0_abs*sin(coef_W); double z2 = exp(coef_B); double z0_abs_2 = z0_abs*z0_abs; a[2] = 1.0/(z2*z0_abs_2); a[0] = (z0_abs_2+2*z0_real*z2)*a[2]; a[1] = -(2*z0_real+z2)*a[2]; *b0 = 1.0 - a[0] - a[1] - a[2]; return 0; }; 

वह सब है! अब, आपको कोड स्वयं लिखने की आवश्यकता है। गणना, निश्चित रूप से, फ्लोट में किए जाने की जरूरत है, लेकिन आधुनिक कंप्यूटर फ्लोटिंग पॉइंट नंबरों पर भरोसा करते हैं (विशेषकर sse के साथ) बहुत जल्दी। इंटेल प्रोग्रामर, वैसे, वेक्टर प्रोसेसर निर्देशों के लिए गॉस-आईआईआर फिल्टर को अनुकूलित करने के लिए ध्यान रखा है, पहले से ही एक संपूर्ण लेख लिखा है । सच है, वे वहाँ एक अलग विधि पर विचार करते हैं, लेकिन मुख्य अनुकूलन विधियों को अच्छी तरह से वर्णित किया गया है।

अंत में, आप एक उदाहरण दे सकते हैं कि क्या हुआ:



चित्र व्यावहारिक रूप से "ईमानदार" से अलग नहीं है। हालाँकि, यदि आप इसे फ़ोटोशॉप में खोलते हैं और ध्यान से अध्ययन करते हैं, तो आप अंतर पा सकते हैं।

_{PS यह वास्तव में हैबे पर मेरी पहली पोस्ट है, मैं कुछ याद कर सकता हूं। यदि आपके कोई प्रश्न हैं, तो मैं टिप्पणियों में उत्तर दूंगा।}