
10 सितंबर 2012 को, रूसी कोड कप 2012 प्रोग्रामिंग चैम्पियनशिप समाप्त हो गई। सब कुछ कैसे हुआ, इसके बारे में एक विस्तृत कहानी
पहले प्रकाशित हुई थी , और आज हम उन कार्यों का विश्लेषण करेंगे जो फाइनलिस्ट को प्रस्तावित किए गए थे। उनमें से केवल छह थे, और उनमें से प्रत्येक एक अलग दिलचस्प कहानी है:
इन समस्याओं को हल करने के लिए तीन घंटे आवंटित किए गए थे। छह में से पांच समस्याओं को हल करने वाला एकमात्र रूसी कोड कप 2012
व्लादिस्लाव एपिफ़ानोव का विजेता था। आधे से भी कम फाइनलिस्टों ने प्रत्येक में चार कार्य पूरे किए। पहले तीन कार्यों ने लगभग सब कुछ किया। केवल एक
एवगेनी कपुन ने कार्ड के डेक के बारे में समस्या को सही ढंग से हल किया। टूर्नामेंट में दूसरा स्थान
नतालिया बोंडारेंको ने लिया, जिन्होंने दूसरों की तुलना में चार समस्याओं को हल किया और कम प्रयासों के साथ।
नाराज पक्षी
Andrey KALININ , Mail.Ru Search Developer
Division के प्रमुख , आपको समस्या कथन के बारे में बताएंगे।
कार्य को "एंग्री बर्ड्स" कहा जाता है। इसका सार सरल है। पंखों की लंबाई का एक तार होता है, जिस पर पक्षी स्थित होते हैं। कुछ पक्षी दाईं ओर जाते हैं, कुछ बाईं ओर। जब वे एक दूसरे से मिलते हैं - वे दिशा बदलते हैं। जब वे तार के अंत तक पहुँचते हैं, तो वे उतार देते हैं। यह निर्धारित करना आवश्यक है कि इनमें से प्रत्येक पक्षी कब उड़ जाएगा। समस्या की स्थितियों के अनुसार, प्रत्येक दिशा में 100,000 पक्षी जा सकते हैं, इसलिए, कुल मिलाकर उनमें से 200,000 से अधिक नहीं हैं।

समस्या का विस्तृत विवरणजैसा कि आप जानते हैं, पक्षी तारों पर बैठना पसंद करते हैं। काउंटी शहर K में एक लंबा तार है जो उन्हें विशेष रूप से पसंद है। एक बिंदु पर, कई पक्षी उस पर बैठे थे। सब कुछ ठीक हो जाएगा, लेकिन केवल तार के नीचे चलने वाले एक सुअर ने धूल के ऐसे बादल को उठाया कि इससे पक्षियों को बहुत गुस्सा आया।
क्रोधित हो कर, पक्षी इस तार के साथ अलग-अलग दिशाओं में चलने लगे - कोई बाईं ओर, कोई दाईं ओर। इस मामले में, सभी पक्षी एक मीटर प्रति मिनट के बराबर गति से चलने लगे। जब दो पक्षी एक दूसरे की ओर बढ़ते हैं, तो वे तुरंत मुड़ जाते हैं और विपरीत दिशा में उसी गति से दौड़ना शुरू करते हैं।
यह प्रक्रिया अनिश्चित काल तक जारी रहेगी, लेकिन केवल तार अंतिम निकला, और जैसे ही पक्षियों में से एक तार के अंत तक पहुंचता है, यह तुरंत बंद हो जाता है, और इस से स्तब्ध अन्य सभी पक्षी, चारों ओर मुड़ते हैं और विपरीत दिशा में चलना शुरू करते हैं। यदि दो पक्षी एक ही समय में किनारे पर दौड़ते हैं, तो दो मोड़ आते हैं, या, जो एक ही है, कुछ भी नहीं होता है।
आपको एक प्रोग्राम लिखने की ज़रूरत है, जो तार की लंबाई के अनुसार, चलने वाले पक्षियों की प्रारंभिक स्थिति और दिशाओं, प्रत्येक पक्षी के लिए पता लगाएगा कि किस समय वह तार से उड़ जाएगा।
इनपुट प्रारूप
पहली पंक्ति में एक पूर्णांक एल (1 ≤ एल) 109) होता है - मीटर में तार की लंबाई।
दूसरी पंक्ति में नंबर n (0 line n) 100 000) है - दाईं ओर चलने वाले पक्षियों की संख्या। तीसरी पंक्ति में n अलग-अलग पूर्णांक होते हैं I (0 <a i <L) - तार के बाएं छोर से मीटर तक की दूरी सही चलने वाले पक्षियों तक।
चौथी पंक्ति में संख्या m (0 line m) 100 000) है - बाईं ओर चलने वाले पक्षियों की संख्या। पांचवीं पंक्ति में एम अलग-अलग पूर्णांक हैं I (0 <b i <L) - तार के बाएं छोर से मीटर में दूरी जो बाईं ओर चल रहे पक्षियों के लिए है।
कोई भी दो पक्षी मूल रूप से एक ही स्थान पर नहीं हैं। यह गारंटी है कि कम से कम एक पक्षी तार पर बैठता है।
आउटपुट स्वरूप
पहली पंक्ति में n पूर्णांक प्रिंट करें i - कितने मिनट के बाद इनपुट विवरण में दाईं ओर उड़ान भरने वाला i-th पक्षी विवरण के क्रम में उड़ जाएगा। दूसरी पंक्ति में प्रिंट मी पूर्णांक u मैं - कितने मिनट के बाद इनपुट में विवरण के क्रम में बाईं ओर उड़ान भरने वाला i-th पक्षी उड़ जाएगा।
2 सेकंड की समय सीमा
256 एमबी मेमोरी सीमा
समस्या में एक उदाहरण दिया गया था। इसके निर्माण और समाधान को स्पष्ट करने के लिए, इस उदाहरण पर हर मिनट पक्षियों की आवाजाही को ट्रैक करना उपयोगी होगा। यह निम्नलिखित इनपुट प्रदान करता है: दो पक्षी 8 वें और 9 वें मीटर पर हैं और दाईं ओर जाते हैं, तीन और पक्षी 2, 5 वें और 7 वें मीटर पर हैं और बाईं ओर जाते हैं। तार की लंबाई 10 मीटर है। यह प्रारंभिक स्थिति है। यह गणना करना आवश्यक है कि एक पक्षी कब उड़ जाएगा।
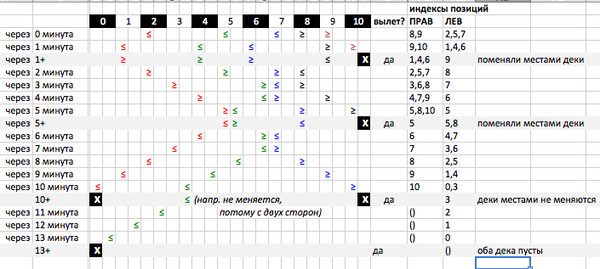
जैसा कि आप देख सकते हैं, पहले और पांचवें मिनट में, पक्षी दाहिने छोर से दूर उड़ते हैं, दसवें में दो पक्षी एक बार में उड़ते हैं, और तेरहवें में आखिरी उड़ जाता है।
यहां यह ध्यान रखना महत्वपूर्ण है कि पक्षियों का क्रम कभी नहीं बदलता है। यह भी ध्यान दें कि, पक्षियों द्वारा वर्णित ज़िगज़ैग के बावजूद, बाएं या दाएं चलने वाले पक्षियों की संख्या उनकी टक्कर पर निर्भर नहीं करती है, और आंदोलन के निर्देशांक में परिवर्तन की प्रकृति हमेशा रैखिक रहती है। यह पहले से पांचवें मिनट के अंतराल में स्पष्ट रूप से दिखाई देता है, जब पहले से ही तीन टकराव थे।
दो स्तंभों में दाईं ओर मैंने पक्षियों की स्थिति का संकेत दिया। यह तुरंत स्पष्ट हो जाता है कि तार से पहले टेक-ऑफ के क्षण की भविष्यवाणी की जा सकती है - पक्षी के तार के अंत तक मिनटों की संख्या (= मीटर की संख्या) निकटतम छोरों में से एक के करीब।
यह भी देखा जाता है कि टेक-ऑफ के बाद, सभी आंदोलन आंदोलन को दाईं ओर बांधे जाते हैं, और बाईं ओर आंदोलन के लिए निर्देशांक बन जाते हैं।
नतीजतन, समस्या का समाधान दो डेक को बनाए रखने के लिए कम हो गया है - "डबल-एंडेड कतार" प्रकार की डेटा संरचनाएं, जिसमें पहले या अंतिम तत्व को हटाने के लिए ओ (1) में प्रदर्शन किया जाता है। जब कोई पक्षी उड़ान भरता है, तो चरम तत्व को डेक से हटा दिया जाता है, और डेक स्वयं स्वैप हो जाते हैं। जोड़े रखना <दिसंबर; आपको इसमें कितनी संख्याओं को जोड़ना होगा> आप O (1) में पा सकते हैं कि अगला पक्षी कितनी देर और किस दिशा में उड़ान भरेगा। चूंकि पक्षियों का क्रम नहीं बदलता है, आपको अतिरिक्त रूप से पक्षियों के मूल स्थान के निर्देशांक के एक क्रमबद्ध सरणी को संग्रहित करना चाहिए ताकि यह निर्धारित किया जा सके कि किस तार ने पक्षियों को तार छोड़ दिया है।
सबसे सुंदर समाधान पायथन 3 में से एक है:
from collections import deque length = int(input()) n = int(input()) right = deque(sorted(map(int, input().split()))) m = int(input()) left = deque(sorted(map(int, input().split()))) addLeft, addRight = 0, 0 INF = 2*10**9 ans = 0 while right or left: L = left[0] + addLeft if left else INF R = length - (right[-1] + addRight) if right else INF m = min(L, R) ans += m addLeft -= m addRight += m if L < R: left.popleft() left, addLeft, right, addRight = right, addRight, left, addLeft elif L == R: left.popleft() right.pop() else: right.pop() left, addLeft, right, addRight = right, addRight, left, addLeft print (ans)
चिड़ियों के साथ काम सबसे पहले
मिखाइल KEVER ने राउंड की शुरुआत से 22 वें मिनट तक किया था। कुछ सेकंड के बाद,
वासिल बिलसेट ने कार्य को पारित कर दिया।
कुल मिलाकर, 40 लोगों ने कार्य का सामना किया, 11 लोगों ने इसे हल करना शुरू किया। इसे हल करने का औसत समय 30 मिनट है। इनमें से, हल करने के लिए सबसे बड़ा समय 44 मिनट है (उन स्थितियों की गणना नहीं जहां कोई समाधान नहीं भेजा गया था)। सभी 11 लोग जिन्होंने पहले के पहले कार्य को सफलतापूर्वक हल किया कम से कम दो और। 11 में से 2 मामलों को छोड़कर, वे सभी कार्य बी में गए, और फिर सी को कार्य करने के लिए, अर्थात्, उन्होंने वर्णमाला क्रम में कार्यों को पूरा किया। यह कार्य उन सभी कार्यों में तीसरे स्थान पर है जिनके साथ यह प्रतियोगिता शुरू हुई थी।
Trisoliantsy
ऑलोड्स ऑनलाइन के तकनीकी निदेशक,
इल्या वायसमैन , त्रिसोलियन कार्य के बारे में बताते हैं:
समस्या की स्थिति के अनुसार, त्रिसोल ग्रह के कुछ निवासी अपनी उम्र को एक ही पूर्णांक के रूप में निर्दिष्ट नहीं करते हैं, जैसे कि हम मनुष्य, लेकिन के पूर्णांक के वेक्टर के रूप में। एक नवजात शिशु ट्रिसोलियन में, उम्र के वेक्टर में एक शून्य होता है, लेकिन बड़े होने के प्रत्येक वर्ष के साथ, आयु वेक्टर के प्रत्येक तत्व में एक निश्चित सकारात्मक संख्या जोड़ी जाती है। ट्रिसोलियन की जीवन कहानी सभी उम्र के वैक्टर का एक सेट है जो उनके जीवन भर थी। यह सर्वविदित है कि एक ही कहानी वाले ट्रिसोलियन मौजूद नहीं हैं। वैज्ञानिक ट्रिसोलियन की अधिकतम संख्या में रुचि रखते हैं जिनकी जीवन कहानी एक वेक्टर पर समाप्त होती है जिसका तत्वों का योग n है। आपको एक प्रोग्राम लिखने की ज़रूरत है जो इस मान को मापता है एक प्रमुख संख्या 7340033 = 7 * 2 ^ 20 + 1।
उदाहरण के लिए, k = 2 के लिए 8 ट्रिसोलियन हो सकते हैं, जिनकी जीवन कहानी 5 के योग के साथ एक वेक्टर पर समाप्त होती है।
1. (0, 0) - (1, 1) - (2, 3);
2. (0, 0) - (1, 1) - (3, 2);
3. (0, 0) - (1, 2) - (2, 3);
4. (0, 0) - (1, 4);
5. (0, 0) - (2, 1) - (3, 2);
6. (0, 0) - (2, 3);
7. (0, 0) - (3, 2);
8. (0, 0) - (4, 1)।
समस्या का विस्तृत विवरणहाल ही में यह ज्ञात हुआ कि ट्रिसोल ग्रह के निवासी हमारी उम्र को एक पूर्णांक के रूप में नहीं दर्शाते हैं, जैसा कि हम मनुष्य हैं, लेकिन के पूर्णांक के वेक्टर के रूप में। यह माना जाता है कि एक नवजात शिशु ट्रिसोलियन में, उसकी उम्र के एक वेक्टर में कश्मीर शून्य होता है। जैसे-जैसे वे बड़े होते हैं, हर साल, उम्र के वेक्टर के प्रत्येक तत्व में एक सकारात्मक संख्या जोड़ी जाती है।
ट्रिसोलियन जीवन कहानी उनकी उम्र के सभी वैक्टर का सेट है जो उन्होंने अपने जीवन के दौरान की थी। पृथ्वी वैज्ञानिकों ने स्थापित किया है कि एक ही कहानी के साथ दो ट्रिसोलियन नहीं हैं।
अब वैज्ञानिक रुचि रखते हैं कि ट्रिसोलियन की अधिकतम संख्या क्या है जिसकी जीवन कहानी एक वेक्टर पर समाप्त होती है जिसका तत्वों का योग n है। एक प्रोग्राम लिखें जो इस मान को मापता है एक प्रमुख संख्या 7340033 = 7 · 220 + 1।
इनपुट प्रारूप
पहली पंक्ति में दो पूर्णांक n और k हैं - अंतिम आयु वेक्टर के तत्वों का योग, और वेक्टर में तत्वों की संख्या (1 (n 23 4239, 1 ≤ k 9 10 9 )।
आउटपुट स्वरूप
ट्रिसोलियन की अधिकतम संख्या प्रिंट करें जिनकी जीवन कहानी एक वेक्टर पर समाप्त हो सकती है जिनके तत्वों का योग n है। उत्तर को मॉडुलो 7340033 = 7 · 2 20 + 1 घटाया जाना चाहिए।
 थोड़ा ऐतिहासिक पृष्ठभूमि, जिसके बिना समस्या का समाधान संभव नहीं है। ट्रिसोलियन ग्रह ट्राइसोल के निवासी हैं, जो गैलेक्सी ऑफ़ हॉरर में फॉरबिडन ज़ोन के अंदर गहरे स्थित हैं। वे 100% तरल हैं। आसानी से अपना आकार बदलने में सक्षम। साधारण निवासी शांतिपूर्ण हैं, जो सत्तारूढ़ अभिजात वर्ग के बारे में नहीं कहा जा सकता है। समय-समय पर वे एक-दूसरे को पीते हैं, इस तरह से कैरियर की सीढ़ी के साथ आगे बढ़ते हैं।
थोड़ा ऐतिहासिक पृष्ठभूमि, जिसके बिना समस्या का समाधान संभव नहीं है। ट्रिसोलियन ग्रह ट्राइसोल के निवासी हैं, जो गैलेक्सी ऑफ़ हॉरर में फॉरबिडन ज़ोन के अंदर गहरे स्थित हैं। वे 100% तरल हैं। आसानी से अपना आकार बदलने में सक्षम। साधारण निवासी शांतिपूर्ण हैं, जो सत्तारूढ़ अभिजात वर्ग के बारे में नहीं कहा जा सकता है। समय-समय पर वे एक-दूसरे को पीते हैं, इस तरह से कैरियर की सीढ़ी के साथ आगे बढ़ते हैं।यह कार्य अपेक्षाकृत सरल है, क्योंकि इसका सारा समाधान कॉम्बिनेटरिक्स में आता है। दूसरी ओर, यह तुरंत इतना सरल नहीं हो जाता है क्योंकि ऐसा लगता है कि यदि आप कश्मीर की संभावित सीमा को करीब से देखते हैं - वेक्टर का आयाम (1 (k 0000 10000000000)।
| एन = 2 | एन = 3 | एन = 4 | एन = 5 | एन = 6 |
| (0,0) - (1,1) | (0,0) - (1,2)
(0,0) - (2,1) | (0,0) - (1,1) - (2,2)
(0,0) - (2,2)
(0,0) - (3,1)
(0,0) - (1,3)
| (0, 0) - (1, 1) - (2, 3);
(0, 0) - (1, 1) - (3, 2);
(0, 0) - (1, 2) - (2, 3);
(0, 0) - (2, 1) - (3, 2);
(0, 0) - (2, 3);
(0, 0) - (3, 2);
(0, 0) - (4, 1)।
(0, 0) - (1, 4);
| (0,0) - (1,1) - (2,2) - (3,3)
(0,0) - (1,1) - (4,2)
(0,0) - (1,1) - (2,4)
(0,0) - (1,1) - (3,3)
(0,0) - (1,2) - (3,3)
(0,0) - (1,2) - (2,4)
(0,0) - (2,1) - (3,3)
(0,0) - (2,1) - (4,2)
(0,0) - (2,2) - (3,3)
(0,0) - (3,1) - (4,2)
(0,0) - (1,3) - (2,4)
(0,0) - (5,1)
(0,0) - (1,5)
(0,0) - (4,2)
(0,0) - (2,4)
(0,0) - (3,3)
|
| 1 विकल्प | 2 विकल्प | 4 विकल्प | 8 विकल्प | 16 विकल्प |
समाधान को समझने के लिए महत्वपूर्ण विचार यह है कि एन के बड़े मूल्यों के लिए "झाड़ियों" में आंशिक रूप से निचले मूल्यों के समाधान शामिल हैं, जो हमें पुनरावृत्ति के माध्यम से गणना को व्यवस्थित करने की अनुमति देता है।
आलेखीय रूप से, विशेष केस k = 2 के लिए, जीवन कहानी को सेगमेंट के एक सेट के रूप में प्रदर्शित किया जा सकता है, जो लाइन एफ (x) = nx पर अक्ष पर पड़ी सकारात्मक पूर्णांक के निशान के साथ शून्य चिह्न को जोड़ता है।
यहाँ N = 4 का समाधान कैसा दिखता है:
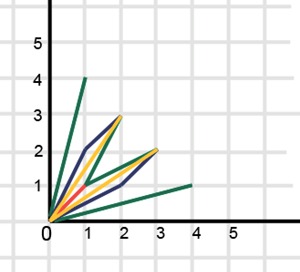
एन = 4 कहानियों के लिए, आठ।
अब हम इस कहानी में वेक्टर (1,1) जोड़ते हैं और प्राप्त करते हैं
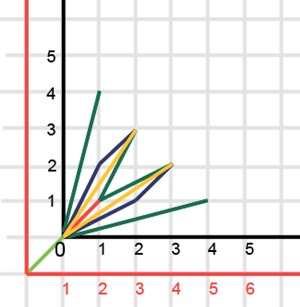
वेक्टर (1,1) से शुरू होने वाली प्रत्येक कहानी N = 7 के लिए कहानी का हिस्सा होगी। कहानी का एक और हिस्सा वेक्टर (1,2), आदि के साथ शुरू होने वाली छोटी "झाड़ियों" होगा।
इसी तरह की कहानी अन्य वैक्टर के साथ। हम वेक्टर (1,3) के लिए एक उदाहरण देते हैं, जो एन = 7 के लिए इतिहास के तत्वों के एक हिस्से की शुरुआत है। इस मामले में, निम्नलिखित सामने आएगा:
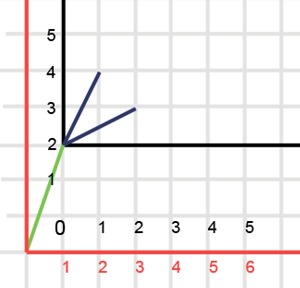
अर्थात्, यदि हम उस वेक्टर को लेते हैं जो उसके जन्म के पहले वर्ष के लिए ट्रिसोलियन को दिया गया था, और इसे ट्रिसोलियन जीवन इतिहास के सभी वैक्टर से घटाया जाता है, तो इस वेक्टर को बाहर फेंकने के बाद, हमें वास्तव में ट्राइसोलियन का कुछ जीवन इतिहास मिलता है, जिसके लिए पिछले वेक्टर के तत्वों का योग n है - (योग) फेंक दिया वेक्टर तत्व)।
इस प्रकार, हम यह समझ सकते हैं कि वे सभी कहानियाँ जिनके लिए अंतिम वेक्टर के तत्वों का योग n है, उन कहानियों से प्राप्त किया जा सकता है जिनमें अंतिम वेक्टर में कुछ m <n के लिए तत्वों का योग है, n के बराबर योग के साथ सकारात्मक तत्वों के कुछ वेक्टर को जोड़ना। जीवन की पूरी कहानी।
एनएम के बराबर राशि वाले कितने वैक्टर होंगे? न्यूनतम वेक्टर प्रत्येक समन्वय में एक को शामिल करता है, इसलिए, कश्मीर के सभी घटकों के सभी वैक्टरों में से, परिणामस्वरूप, एनएम योग दिखाई देता है। अब हमें कश्मीर इकाइयों को निर्देशांक देने की आवश्यकता है। इसे करने के तरीकों की संख्या दोहराव के साथ संयोजन की संख्या है। पुनरावृत्तियों के साथ संयोजन की संख्या की गणना की जाती है
!}{r! (r-1)!})
और पुनरावृत्ति के बिना संयोजन की संख्या के रूप में गणना की जाती है
!})
जिससे यह आसानी से अनुमान लगाया जा सकता है कि बी के माध्यम से पुनरावृत्ति के साथ संयोजन की संख्या दोहराव के बिना संयोजन की संख्या + बी - 1 के बराबर है।
तो हमारे मामले में तरीकों की संख्या n से n - m - k + k - 1 के बराबर है
के, यानी, सी से एन - एम - 1 से कश्मीर।
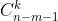 एन के
एन के रूप में वांछित मान को अस्वीकार करते हुए, हम निम्नलिखित पुनरावृत्ति फार्मूला प्राप्त करते हैं:। यह माना जाता है कि ans
0 = 1. एल्गोरिथम का रनिंग टाइम O (n2) है।
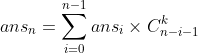
जहाँ C (x, y) पहले में दूसरे तर्क के संयोजन की संख्या है, जिसे x के रूप में परिकलित किया गया है! / (xy)! / य!
Trisolians का कार्य लगभग उन सभी लोगों द्वारा किया गया था जो फाइनल में थे (दो लोगों को छोड़कर)। समस्या को हल करने में लगभग 18 मिनट का समय लगा। ऐसा करने वाले पहले 11 मिनट में
रोमन रिज़वानोव थे, एक छोटे से अंतर के साथ -
एवगेनी कपुन ।
प्रोसेसर
अलेक्जेंडर GORNY , CIO Mail.Ru Group, प्रोसेसर समस्या के बारे में बताएगा:
कार्य में एक निश्चित दोहरे कोर प्रोसेसर शामिल है जो 26 विभिन्न निर्देशों का प्रदर्शन कर सकता है। प्रत्येक निर्देश को अंग्रेजी वर्णमाला के अक्षर में प्रतीकात्मक रूप से लिखा गया है। कार्यक्रमों में निर्देशों का एक सेट शामिल है। यह गणना करना आवश्यक है कि प्रोसेसर को संकेतित 2n प्रोग्राम (बदले में, विशिष्ट निर्देशों के निर्दिष्ट अनुक्रम से मिलकर) को संसाधित करने के लिए किस समय की आवश्यकता होगी, अगर यह ज्ञात है कि, वास्तुकला की ख़ासियत के कारण, एक ही समय में एक ही निर्देशों को दो कोर में निष्पादित किया जा सकता है, और n - ऐसे प्रोसेसर की संख्या।
एक प्रोसेसर दो कार्यक्रमों को एक साथ कैसे संसाधित कर सकता है, इसका एक चित्रण:
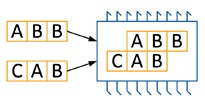
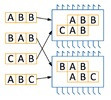
समस्या यह है कि एन प्रोसेसर और दो कोर में 2 एन कार्यक्रमों को कुशलता से कैसे बिखेरना है ताकि चरणों की संख्या कम से कम हो।
समस्या का विस्तृत विवरणजैसा कि आप जानते हैं, वर्तमान में निर्मित अधिकांश प्रोसेसर मल्टी-कोर हैं, अर्थात्, वे एक साथ कई निर्देशों के निष्पादन का समर्थन करते हैं। Paraltel ने एक नए प्रकार का डुअल-कोर प्रोसेसर विकसित किया है जो आपको 26 विभिन्न निर्देशों का पालन करने की अनुमति देता है, जो राजधानी लैटिन अक्षरों में दर्शाए गए हैं। ऐसे प्रत्येक निर्देश के निष्पादन के लिए प्रोसेसर के ठीक एक घड़ी चक्र की आवश्यकता होती है।
इस प्रोसेसर के लिए कार्यक्रम निर्देशों का एक क्रम है। कार्यक्रम निर्देशों को उस क्रम में निष्पादित किया जाना चाहिए जिसमें वे कार्यक्रम का पालन करते हैं, यह निर्देशों को इंटरचेंज करने की अनुमति नहीं है।
दो कोर की उपस्थिति के कारण, प्रोसेसर एक साथ दो कार्यक्रमों को निष्पादित कर सकता है - प्रत्येक कोर पर। हालांकि, वास्तुशिल्प विशेषताओं के कारण, एक ही निर्देश को एक ही प्रोसेसर के दो कोर पर एक साथ निष्पादित किया जा सकता है।
जब प्रोसेसर पर दो प्रोग्राम निष्पादित किए जाते हैं, तो एक विशेष नियंत्रण डिवाइस इस तरह से निष्पादन को अनुकूलित करता है जैसे कि दोनों कार्यक्रमों के निष्पादन को जल्द से जल्द पूरा करने के लिए। उदाहरण के लिए, एबीबी और एबीसी कार्यक्रमों को 4 चक्रों में प्रोसेसर पर निष्पादित किया जा सकता है: पहला, अलग-अलग कोर पर दोनों कार्यक्रमों के कमांड को एक साथ निष्पादित किया जाता है, फिर एक ही समय में बी कमांड, फिर पहले कार्यक्रम से बी कमांड, और अंत में। दूसरे से "सी"। इसी तरह, "CAB" और "BAB" प्रोग्राम 4 चक्रों में चलते हैं।
हाल ही में, कंपनी के विशेषज्ञों ने एन प्रोसेसर से एक सुपर कंप्यूटर को इकट्ठा किया है, जिस पर 2 एन कार्यक्रमों की आवश्यकता होती है। गणना का संगठन ऐसा है कि प्रत्येक प्रोसेसर को इस सेट से ठीक दो कार्यक्रमों को निष्पादित करना होगा, प्रत्येक कोर पर।
आपको एन प्रोसेसर पर 2 एन कार्यक्रमों के निष्पादन की योजना बनाने की आवश्यकता है ताकि सभी कार्यक्रमों के लिए पूरा होने का समय कम से कम हो।
इनपुट प्रारूप
पहली पंक्ति में नंबर n (1 line n - 10) - प्रोसेसर की संख्या है। अगला, 2n लाइनों में, निष्पादित किए जाने वाले प्रोग्राम निर्दिष्ट हैं। प्रत्येक कार्यक्रम में 1 से 100 टीमें शामिल हैं। प्रत्येक आदेश राजधानी लैटिन अक्षरों में दिया गया है।
आउटपुट स्वरूप
एक ही संख्या प्रिंट करें - न्यूनतम समय जिसके लिए सभी कार्यक्रमों को निष्पादित किया जा सकता है।
निम्नलिखित कार्यक्रमों का एक सेट कार्य के लिए एक उदाहरण के रूप में दिया गया है: एबीबी बीएबी सीएबी एबीसी
और जानकारी है कि दो प्रोसेसर हैं।
प्रोग्राम को दो प्रोसेसरों पर चलाने के लिए इन चार चरणों की आवश्यकता होती है:
| सीपीयू 1 कोर 1 | सीपीयू 1 कोर 2 | सीपीयू 2 कोर 1 | सीपीयू 2 कोर 2 |
| [ए] बीबी | [A] ई.पू. | [बी] एबी | |
| ए [बी] बी | ए [बी] सी | | [सी] एबी |
| एबी [बी] | | बी [ए] बी | सी [ए] बी |
| एबी [सी] | बीए [बी] | सीए [बी] |
हम समस्या के समाधान को दो चरणों में विभाजित करते हैं और प्रत्येक पर अलग से विचार करते हैं।
पहला कदम एक ग्राफ बनाने के लिए है। इसके कोने 2n प्रोग्राम हैं जिन्हें हमें निष्पादित करने की आवश्यकता है। ग्राफ़ को भारित किया जाएगा, और दो कार्यक्रमों के बीच किनारे का वजन उस समय की मात्रा के बराबर है जो प्रोसेसर अपने संयुक्त निष्पादन पर खर्च करेगा। यह मान उस प्रोग्राम के योग के बराबर है जो उन कमांड्स को घटाता है जिन्हें एक साथ निष्पादित किया जाएगा। और एलसीएस (ए, बी) की तुलना में ऐसी कोई और कमांड नहीं हैं, जहां ए और बी प्रोग्रामों का वर्णन करने वाली लाइनें हैं, और एलसीएस (
लॉन्गेस्ट कॉमन सबरेंसेंस , सबसे बड़ी सामान्य अनुवर्ती) वह फ़ंक्शन है जो दो अनुक्रमों की सबसे बड़ी सामान्य अनुवर्तीता को खोजती है।
नतीजतन, बढ़त वजन खोजने का कार्य इस तरह दिखेगा:
int dist(String a, String b) { int[][] d = new int[a.length() + 1][b.length() + 1]; for (int[] ar : d) { Arrays.fill(ar, 1000000000); } d[0][0] = 0; for (int i = 0; i <= a.length(); ++i) { for (int j = 0; j <= b.length(); ++j) { if (i < a.length()) { d[i + 1][j] = Math.min(d[i + 1][j], d[i][j] + 1); } if (j < b.length()) { d[i][j + 1] = Math.min(d[i][j + 1], d[i][j] + 1); } if (i < a.length() && j < b.length() && a.charAt(i) == b.charAt(j)) { d[i + 1][j + 1] = Math.min(d[i + 1][j + 1], d[i][j] + 1); } } } return d[a.length()][b.length()]; }
समाधान का दूसरा चरण इस ग्राफ में एक परिपूर्ण मिलान होगा जिसमें अधिकतम किनारे का वजन कम से कम हो। सबसे सरल एल्गोरिदम में से एक जो इस समस्या को हल करता है और समय सीमा में फिट होता है वह गतिशील प्रोग्रामिंग है, लेकिन पहले से ही सबसेट में। आकार के कोने के प्रत्येक सेट के लिए k की तुलना में अधिक नहीं है, हम उत्तर जानते हैं। इस मामले में, ऐसे सभी सेटों से गुजरना और उन सभी संभावित किनारों को जोड़ना जो अभी भी इसमें नहीं हैं, हम आकार के सभी सेटों के उत्तर की गणना k + 2 से अधिक नहीं कर सकते हैं।
int[] d = new int[1 << (2 * n)]; Arrays.fill(d, 1000000000); d[0] = 0; for (int mask = 0; mask + 1 < 1 << (2 * n); ++mask) { if (d[mask] == 1000000000) { continue; } int i = 0; while ((mask & (1 << i)) != 0) { ++i; } for (int j = i + 1; j < 2 * n; ++j) { if ((mask & (1 << j)) == 0) { d[mask | (1 << i) | (1 << j)] = Math.min(d[mask | (1 << i) | (1 << j)], Math.max(d[mask], dist[i][j])); } } }
"प्रोसेसर" कार्य फाइनल में मौजूद लगभग सभी लोगों द्वारा किया गया था (दो लोगों को छोड़कर)। इस समस्या को हल करने का औसत समय लगभग 18 मिनट है। समस्या को हल करने के लिए सबसे पहले 11 वें मिनट में
व्लादिस्लाव EPIFANOV था।
घेराबंदी
"घेराबंदी" कार्य के बारे में NRU ITMO विभाग के एक छात्र
पावेल KROTKOV को बताएगा।
टास्क, एल्डरसबर्ग के शानदार शहर के बारे में बताता है, जिस पर दुश्मनों की भीड़ हमला करने वाली है। शहर को बनाए रखने के लिए, एन कलाकृतियों की एक बाधा डालना आवश्यक है, और एक [i] "मर्लिन" की मात्रा में जादुई ऊर्जा के साथ प्रत्येक i-वें विरूपण साक्ष्य को सक्रिय करना है। उसके बाद, बी [i] "मर्लिन्स" का उपयोग करके, दुश्मन दूर से इस विरूपण साक्ष्य को नष्ट करने में सक्षम हो जाएगा। दुश्मन के शस्त्रागार में शहर के रक्षकों के पास जादुई ऊर्जा है - बी मर्लिन। शहरवासियों ने कलाकृतियों को सक्रिय करने का निर्णय लिया ताकि दुश्मन के जादूगरों द्वारा उनके विनाश के बाद, अधिकतम संख्या में कलाकृतियां सक्रिय रहें। शहर के रक्षकों को यह चुनने में मदद करना आवश्यक है कि कौन सी कलाकृतियों को सक्रिय करना है।
समस्या का विस्तृत विवरणएल्डर्सबर्ग के शानदार शहर के लिए मुश्किल समय आ गया है। मिनट-मिनट से, दुश्मनों के अनगिनत गिरोह हमले पर जाएंगे। केवल जादुई बाधाएं शहर को पकड़ने में मदद कर सकती हैं।
बाधा डालने के लिए शहर के रक्षकों के शस्त्रागार में एन कलाकृतियां हैं। I-th विरूपण साक्ष्य को सक्रिय करने के लिए, एक i मर्लिन (जादुई ऊर्जा की इकाइयां) की आवश्यकता होती है। उसके बाद, b i merlins का उपयोग करके, दुश्मन दूर से कलाकृतियों को नष्ट कर सकता है।
शहर के रक्षकों के पास जादुई ऊर्जा का एक मग्लिन है, जो शत्रु बी मर्लिन के शस्त्रागार में है। जादुई ऊर्जा भंडार की भरपाई नहीं की जाती है। शहरवासियों ने कलाकृतियों को सक्रिय करने का फैसला किया ताकि दुश्मन के जादूगरों द्वारा उनके विनाश के बाद, अधिकतम संख्या सक्रिय रहे।
शहर के रक्षकों को सक्रिय करने के लिए कौन सी कलाकृतियों को चुनने में मदद करें।
इनपुट प्रारूप
पहली पंक्ति में तीन पूर्णांक A, B और n (0 B A, B, 105, 0 ≤ n by 1000) हैं, जो रिक्त स्थान द्वारा अलग किए गए हैं। अगली n लाइनों में संख्या ai और bi (1 i a i , b i ) 105) के जोड़े हैं।
आउटपुट स्वरूप
पहली पंक्ति में उन कलाकृतियों की संख्या प्रिंट करें जो संघर्ष के दोनों पक्षों के इष्टतम कार्यों के दौरान सक्रिय रहेंगी। दूसरी पंक्ति में उन कलाकृतियों की संख्या प्रिंट करें जिन्हें शहर के रक्षकों को सक्रिय करना चाहिए, और इन कलाकृतियों की संख्या। रिक्त स्थान के साथ एक पंक्ति पर अलग संख्या।
कलाकृतियों को उस क्रम में एक से शुरू किया जाता है जिसमें वे इनपुट में निर्दिष्ट होते हैं।
 थोड़ी ऐतिहासिक पृष्ठभूमि। एल्डर्सबर्ग चार उत्तरी राज्यों में से एक में दूसरा सबसे बड़ा शहर है, Aedirne, दुनिया के बहुत किनारे पर स्थित है। एल्डर्सबर्ग शहर का निर्माण किले की दीवारों के चारों ओर किया गया था, जो कि एडीरन (आंद्रेजेज सपकोव्स्की) की सीमाओं की रक्षा करता था।
थोड़ी ऐतिहासिक पृष्ठभूमि। एल्डर्सबर्ग चार उत्तरी राज्यों में से एक में दूसरा सबसे बड़ा शहर है, Aedirne, दुनिया के बहुत किनारे पर स्थित है। एल्डर्सबर्ग शहर का निर्माण किले की दीवारों के चारों ओर किया गया था, जो कि एडीरन (आंद्रेजेज सपकोव्स्की) की सीमाओं की रक्षा करता था।मान लीजिए कि शहर के रक्षकों ने कई कलाकृतियों को सक्रिय किया है। अपने दुश्मनों के लिए इष्टतम रणनीति बढ़ती बी
i के क्रम में उन्हें नष्ट करना होगा। दरअसल, दुश्मन का लक्ष्य अधिक से अधिक कलाकृतियों को नष्ट करना है। अविनाशी कलाकृतियों पर बहुत सारी ऊर्जा खर्च करने का कोई मतलब नहीं है, जब तक कि एक आसान लक्ष्य नहीं है।
हम गैर-घटते क्रम में कलाकृतियों का पुनर्निर्माण करते हैं
i । यह बता दें कि पहला विरूपण साक्ष्य, जिसे दुश्मन रक्षकों के इष्टतम कार्यों से नष्ट नहीं कर सकता है, नंबर k है। हम इस धारणा के आधार पर, रक्षकों के कार्यों का वर्णन करते हैं। पहले k - 1 कलाकृतियों से, कई का चयन किया जाना चाहिए ताकि उनके विनाश पर खर्च की जाने वाली कुल ऊर्जा कम से कम B - b
k +1 मर्लिन हो, और सक्रियण ऊर्जा न्यूनतम हो। K- वें कलाकृतियों को सक्रिय करें। अंत में, हम ऊर्जा की बढ़ती खपत के क्रम में अंतिम n - k कलाकृतियों को सक्रिय करते हैं।
दुर्भाग्य से, k पहले से ज्ञात नहीं है। हम पहले विरूपण साक्ष्य की संख्या को हल करेंगे जो दुश्मन को नष्ट नहीं कर सकता है, और इस धारणा के लिए इष्टतम उत्तर का निर्माण करेगा।
बता दें कि डी
आईजे न्यूनतम ऊर्जा है जो कलाकृतियों को सक्रिय करने के लिए आवश्यक है, जिनकी संख्या I (1000 तक) से अधिक नहीं है, जैसे कि उनके विनाश के लिए जादुई ऊर्जा के मेरलिंस (100000 तक) की आवश्यकता होगी। संक्रमण: D
i, j = min (D
i - 1 , j, D
i - 1 , j - b
i + a
i )। ये दो मामले इस बात के अनुरूप हैं कि क्या इष्टतम डी
आईजे प्राप्त करने के लिए विरूपण साक्ष्य संख्या I को सक्रिय किया जाना चाहिए।
सरणी डी से हम दुश्मन को के-वें विरूपण साक्ष्य को नष्ट करने में सक्षम नहीं होने के लिए आवश्यक ऊर्जा पाते हैं। उसके बाद, हम उत्सुकता से आराम करते हैं, जबकि सक्रिय करने के लिए पर्याप्त ऊर्जा है। परिणामस्वरूप, सभी k से गुजरते हुए, हम इष्टतम उत्तर पाते हैं।
वर्णित दृष्टिकोण का चलने का समय ओ (एन (बी + एन)) है। इसे पूर्ण समाधान में बदलने के लिए, आपको उत्तर को पुनर्स्थापित करने के लिए सूचना संग्रहण को जोड़ने की आवश्यकता है, जो कि स्पर्शोन्मुख व्यवहार को प्रभावित नहीं करता है।
समाधान में आने वाली अड़चन, इस्तेमाल की जाने वाली मेमोरी हो सकती है। ध्यान दें कि केवल अंतिम पंक्ति को डी सरणी पर संग्रहीत किया जा सकता है। इसके अलावा, प्रत्येक जोड़ी (i, j) के लिए यह जानना पर्याप्त है कि क्या इष्टतम डी
आईजे प्राप्त करने के लिए विरूपण साक्ष्य संख्या I को सक्रिय करना आवश्यक है। स्मृति सीमाओं को पूरा करने के लिए, इस बिट जानकारी को संग्रहीत करने के लिए दो से अधिक बाइट्स का उपयोग करना आवश्यक था।
घेराबंदी का काम 19 लोगों द्वारा हल किया गया था।
पीटर MITRICHEV ने इस कार्य को 87 वें मिनट में
सबसे तेज किया (घेराबंदी के कार्य से पहले, पीटर सफलतापूर्वक पहले तीन में उत्तीर्ण हुआ)।
घसीटना डेक
NRU ITMO के छात्र
सर्गेई मेल्नेवोव डेक को मिलाने के कार्य के बारे में बात करते हैं:
इस कार्य में, आपको डेक मिक्सिंग मैकेनिज्म के बारे में सोचने की जरूरत है, जो आपको इसे पूरी तरह से मिक्स करने की अनुमति देता है (डेक के मध्य से अंत तक कार्ड ब्लॉक्स की न्यूनतम संख्या के लिए (अर्थात, सुनिश्चित करें कि कोई भी दो समान कार्ड एक के बाद एक नहीं चलते हैं, या रिपोर्ट करते हैं कि डेक को पूरी तरह से मिक्स करना असंभव है) । प्रारंभ में, डेक गैर-घटती गरिमा द्वारा सॉर्ट किया जाता है। कार्ड के विभिन्न फायदों की संख्या, डेक में कार्ड के क्रम, डेक की संख्या को देखते हुए।
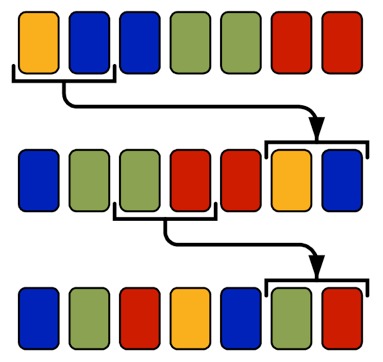
समस्या का विस्तृत विवरणस्वचालन और कम्प्यूटरीकरण तेजी से हमारे जीवन के सभी क्षेत्रों पर आक्रमण कर रहे हैं। , , — . — .
, , 1 t. , .
. , 1, — t. , , .
, .
, : i j , i- j- .
, , .
x — , . x .
. n — . n , . , , 1.
200000.
, , «-1», , , . , k — , . k , i j — , , .
हम संघर्ष को कहेंगे , एक ऐसी स्थिति जिसमें दो समान कार्ड एक पंक्ति में खड़े होते हैं: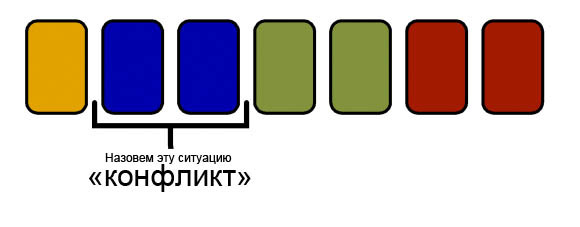 हम शरीर को कार्ड के प्रारंभिक अनुक्रम कहते हैं, जिसे हम कार्ड को पूंछ में स्थानांतरित करके धीरे-धीरे कम कर देंगे। पूंछ इस तरह से बनाई जाएगी कि इसमें कार्ड संघर्ष नहीं बनाते हैं।
हम शरीर को कार्ड के प्रारंभिक अनुक्रम कहते हैं, जिसे हम कार्ड को पूंछ में स्थानांतरित करके धीरे-धीरे कम कर देंगे। पूंछ इस तरह से बनाई जाएगी कि इसमें कार्ड संघर्ष नहीं बनाते हैं।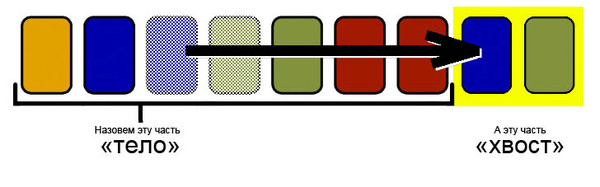 हम मूल अनुक्रम को संघर्षों के अनुक्रम में बदलते हैं और नए अनुक्रम के साथ काम करेंगे। हम संघर्ष के रंग को कार्ड पर लिखे संख्या को कहेंगे जो इसे बनाते हैं। हर बार कार्ड के एक सेगमेंट को डेक के अंत तक स्थानांतरित करते हुए, हम संघर्षों के अंदर इसके सिरों को चुनेंगे।
हम मूल अनुक्रम को संघर्षों के अनुक्रम में बदलते हैं और नए अनुक्रम के साथ काम करेंगे। हम संघर्ष के रंग को कार्ड पर लिखे संख्या को कहेंगे जो इसे बनाते हैं। हर बार कार्ड के एक सेगमेंट को डेक के अंत तक स्थानांतरित करते हुए, हम संघर्षों के अंदर इसके सिरों को चुनेंगे।K. , ⌈K / 2⌉ ( ⌊…⌋ ⌈…⌉ — ).
M «». , M = ⌈K / 2⌉.
, .
, 1122333344 3 ( 33), – 6. M = ⌈K / 2⌉.( ) :
- K — ( ). , «» A, «» B, — C. |A| + |B| + |C| = |K|, |A| + |C| = |B| = M. 1122333344 AABBBC.
: (B, C), , — (A, B). , (B, C)* (A, B)*, * — .
:
1122333344 (AABBC) ->1122333-4.34 (AAB) -> 1-2333-4.3412 (BB)
( , . – )
, . : |C| > 0, C , B. |C| = 0, (A, B)*, B .
- K — . . A, , A-. C, C- , .
, ⌈K / 2⌉. , , «» ( ). .
. Q.
- Q = 0. , .
- Q > ⌈N / 2⌉, . , Q−1 , .
- Q = ⌈N / 2⌉ . , . :
, A- C-
- a = 0 . c = N − Q = ⌊N / 2⌋, , , b c , .
- = 0 . .
- a > 0, b > 0 - a − 1 , B: b − 1, C: c − 1. (a − 1) + (c − 1) = N − Q − 2, Q − 1 , , .
- M < ⌊ ( N + 1) / 2 ⌋ . ( ), , .
, ( ) (C
1 , C
2 ). , , . , .
, . Z, (X, Z) Z , Z Z (X
1 , Z) (X
2 , Z)…. Z- , (X, Y) , (X
k , Z) (X
k+1 , Y), X
k+1 ≠ Z.
, (X, Z) X Z (M). M ≠ Z, Z (X, Z) (Z, ...) , Z M, (X, Z) (M, Z).
, , ⌈K / 2⌉ .
, , , . , O(N log N). , - , , . , , , : . O(n), .
« »
.
():
N . , , .
, . , . , , , . , , .
, .
, , .
, .
3 258 , –1000 1000, .
Russian Code Cup .
— .
.
, . , , , . , .
, . , .
, . , , , , .
, . , , .
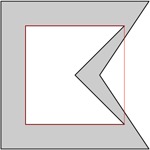
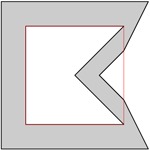
, . , . , . .
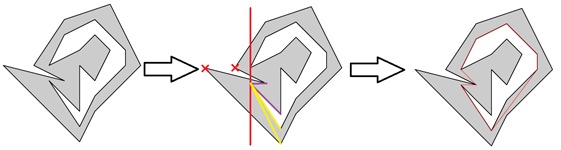
. , — . .
O(n
3 ) , O(n
2 ) O(n) . O(n) O(n
2 ) O(n
2 ). , O(n
3 ).
« » .
, 93- .
Russian Code Cup 2012 . , , , - ( ,
,
), – - (
) . , , , . , , , , ?
अलाइव रऊफ
अनुसंधान और शिक्षा निदेशक
Mail.Ru Group