👽 👩🏿‍🚒 📧 बहुराष्ट्रीय गुणांक की गणना के लिए तरीके 🙈 🐱 👈🏻

एक दिन, गणित में लोकप्रिय प्रश्नोत्तर के माध्यम से स्क्रॉल करते हुए ( math.stackexchange.com ), मुझे बहुराष्ट्रीय गुणांकों की गणना करने के बारे में एक प्रश्न मिला और उसने मेरी दिलचस्पी दिखाई। उन लोगों के लिए ध्यान दें जो नहीं जानते कि यह क्या है, एक विकिपीडिया लेख है। तो, आपको निम्नलिखित अभिव्यक्ति की गणना करने की आवश्यकता है:

ऐसा लग रहा था, इस तरह के एक सरल कार्य का समाधान करने के लिए क्यों? इसका उत्तर यह है कि सबसे सरल अनुभवहीन तरीका, जिसमें योग के गुणन को गुणा करना और फिर इसे भाज्य के गुणन से विभाजित करना शामिल नहीं है, क्योंकि मध्यवर्ती गणना यूंट के थोड़ा ग्रिड या यहां तक कि ऊपरी प्रकार से परे जाती है, हालांकि परिणाम भीतर हो सकता है इन प्रकारों के मान। मुझे यह कार्य पसंद आया, और मैं तुरंत इसे हल करने के लिए बैठ गया और तीन तरीकों के साथ आया। अन्य दो विधियाँ मैंने अन्य उत्तरों से उधार ली हैं। तो, लेख उन सभी विधियों के विवरण और तुलना के बारे में होगा जिन्हें मैंने C # के तहत .NET में लागू किया था।

बड़ी संख्या
टेबुलर तरीका
द्विपद गुणांक के गुणन
योग और लघुगणक का अंतर
कार्यों की मात्रा और अंतर "तथ्यात्मक का लघुगणक"
मेरा रास्ता

आगे, मैं प्रत्येक विधि का वर्णन करूँगा।

बड़ी संख्या

बेशक, पहली बात जो दिमाग में आई, वह एक विशेष प्रकार का बिगइंटर का उपयोग था, जो अंकों की एक मनमानी संख्या के साथ संख्याओं को संग्रहीत करने में सक्षम था। लेकिन यह, सबसे पहले, खेल नहीं है, और, दूसरी बात, सभी भाषाओं में ऐसे प्रकारों के लिए समर्थन नहीं है (हालांकि निश्चित रूप से आप इसे खुद लिख सकते हैं), लेकिन यह विधि निश्चित रूप से हमेशा सही परिणाम देती है, अन्य विधियों के विपरीत जिसमें गोलाई। वैसे, यह संपत्ति आपको अन्य तरीकों की सटीकता का परीक्षण करने की अनुमति देती है, जिस पर बाद में चर्चा की जाएगी।

इस पद्धति का कोड एक भोले कार्यान्वयन से अलग नहीं है, सिवाय इसके कि यूंट प्रकारों के बजाय हर जगह BigInteger है। इसलिए, यह विशेष रुचि का नहीं है।

बिगइंटर स्रोत

public static BigInteger BigAr(uint[] numbers) { BigInteger numbersSum = 0; foreach (var number in numbers) numbersSum += number; BigInteger nominator = Factorial(numbersSum); BigInteger denominator = 1; foreach (var number in numbers) denominator *= Factorial(new BigInteger(number)); return nominator / denominator; } public static BigInteger Factorial(BigInteger n) { BigInteger result = 1; for (ulong i = 1; i <= n; i++) result = result * i; return result; }

तालिका विधि

इसमें Microsoft Excel, wolframalpha.com या अन्य तृतीय-पक्ष कार्यक्रमों / सेवाओं में दिए गए तर्कों से सभी बहुराष्ट्रीय गुणांक की गणना करना और स्रोत कोड में या एक अलग फ़ाइल में गणना गुणांक दर्ज करना शामिल है। इस दृष्टिकोण के नुकसान स्पष्ट हैं: उच्च स्मृति खपत, गुणांक की गणना तर्कों के सभी स्वीकार्य संभव मूल्यों से नहीं। हालांकि, इस पद्धति का प्रदर्शन, शीर्ष पर है। एक तरीका या दूसरा, मैंने इस पद्धति को लागू नहीं किया है।

द्विपद गुणांक

इस विधि में निम्न सूत्र के अनुसार कई द्विपद गुणांक के उत्पाद में बहुपद गुणांक की अभिव्यक्ति को विघटित करना शामिल है:

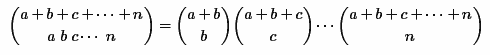
लेकिन यहां, अंतिम द्विपद गुणांक की गणना करते समय फिर से अतिप्रवाह संभव है। इसे होने से रोकने के लिए, निम्न सूत्र का उपयोग करके प्रत्येक द्विपद गुणांक की पुनरावर्ती गणना के लिए एक एल्गोरिथ्म का उपयोग किया जाता है:

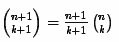
सी # कोड इस तरह दिखता है:

द्विपद स्रोत

 public static ulong BinomAr(uint[] numbers) { if (numbers.Length == 1) return 1; ulong result = 1; uint sum = numbers[0]; for (int i = 1; i < numbers.Length; i++) { sum += numbers[i]; result *= Binominal(sum, numbers[i]); } return result; } public static ulong Binominal(ulong n, ulong k) { ulong r = 1; ulong d; if (k > n) return 0; for (d = 1; d <= k; d++) { r *= n--; r /= d; } return r; }

लघुगणक

इस विधि में मूल सूत्र को मूल राशि के रूप में निम्नानुसार और अंतर में विघटित करना शामिल है:

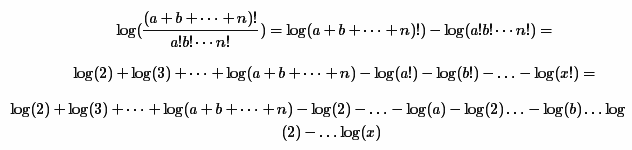
बहुत अंत में, निश्चित रूप से, परिणामी डिग्री के लिए ई को उठाना आवश्यक है, जो परिणाम होगा। एक छोटा अनुकूलन भी किया गया था, जिसमें अंश और हर से हर के अधिकतम भाज्य को छोड़ने में शामिल था। बाद की गणना में तेजी लाने के लिए, सभी लॉगरिदम को सूची में कैश्ड किया जाता है (इस अनुकूलन का प्रदर्शन लेख के अंत में परीक्षण किया जाता है)।

लॉग स्रोत

 static List<double> Logarithms = new List<double>(); public static ulong Log(params uint[] numbers) { return LogAr(numbers); } public static ulong LogAr(uint[] numbers) { int maxNumber = (int)numbers.Max(); uint numbersSum = 0; foreach (var number in numbers) numbersSum += number; double sum = 0; for (int i = 2; i <= numbersSum; i++) { if (i <= maxNumber) { if (i - 2 >= Logarithms.Count) { var log = Math.Log(i); Logarithms.Add(log); } } else { if (i - 2 < Logarithms.Count) sum += Logarithms[i - 2]; else { var log = Math.Log(i); Logarithms.Add(log); sum += log; } } } var maxNumberFirst = false; foreach (var number in numbers) if (number == maxNumber && !maxNumberFirst) maxNumberFirst = true; else for (int i = 2; i <= number; i++) sum -= Logarithms[i - 2]; return (ulong)Math.Round(Math.Exp(sum)); }

गुटों से लघुगणक

यह विधि पिछले एक से लगभग भिन्न नहीं है, सिवाय इसके कि लघुगणक के योग में तथ्यात्मक लघुगणक को विघटित करने के बजाय, गामा फ़ंक्शन से एक विशेष लघुगणक फ़ंक्शन का उपयोग किया जाता है, जिसके कार्यान्वयन को अल्जीब के साथ लिया गया था। वास्तव में, अन्य, छोटे कार्यान्वयन हैं (उदाहरण के लिए, मैथ.नेट में), लेकिन मुझे यह प्रतीत होता है कि यदि एल्गीब में कार्यान्वयन कोड का आकार सबसे बड़ा है, तो कार्यान्वयन स्वयं सबसे सटीक है।

लोगगामा स्रोत

 static Dictionary<uint, double> LnFacts = new Dictionary<uint, double>(); public static ulong LogGammaAr(uint[] numbers) { int maxNumber = (int)numbers.Max(); double value; double denom = 0; uint numbersSum = 0; foreach (var number in numbers) { numbersSum += number; if (LnFacts.TryGetValue(number, out value)) denom += value; else { value = LnGamma(number + 1); LnFacts.Add(number, value); denom += value; } } double numer; if (LnFacts.TryGetValue(numbersSum, out value)) numer = value; else { value = LnGamma(numbersSum + 1); LnFacts.Add(numbersSum, value); numer = value; } return (ulong)Math.Round(Math.Exp(numer - denom)); } public static double LnGamma(double x) { double sign = 1; return LnGamma(x, ref sign); } public static double LnGamma(double x, ref double sgngam) { double result = 0; double a = 0; double b = 0; double c = 0; double p = 0; double q = 0; double u = 0; double w = 0; double z = 0; int i = 0; double logpi = 0; double ls2pi = 0; double tmp = 0; sgngam = 0; sgngam = 1; logpi = 1.14472988584940017414; ls2pi = 0.91893853320467274178; if ((double)(x) < (double)(-34.0)) { q = -x; w = LnGamma(q, ref tmp); p = (int)Math.Floor(q); i = (int)Math.Round(p); if (i % 2 == 0) { sgngam = -1; } else { sgngam = 1; } z = q - p; if ((double)(z) > (double)(0.5)) { p = p + 1; z = p - q; } z = q * Math.Sin(Math.PI * z); result = logpi - Math.Log(z) - w; return result; } if ((double)(x) < (double)(13)) { z = 1; p = 0; u = x; while ((double)(u) >= (double)(3)) { p = p - 1; u = x + p; z = z * u; } while ((double)(u) < (double)(2)) { z = z / u; p = p + 1; u = x + p; } if ((double)(z) < (double)(0)) { sgngam = -1; z = -z; } else { sgngam = 1; } if ((double)(u) == (double)(2)) { result = Math.Log(z); return result; } p = p - 2; x = x + p; b = -1378.25152569120859100; b = -38801.6315134637840924 + x * b; b = -331612.992738871184744 + x * b; b = -1162370.97492762307383 + x * b; b = -1721737.00820839662146 + x * b; b = -853555.664245765465627 + x * b; c = 1; c = -351.815701436523470549 + x * c; c = -17064.2106651881159223 + x * c; c = -220528.590553854454839 + x * c; c = -1139334.44367982507207 + x * c; c = -2532523.07177582951285 + x * c; c = -2018891.41433532773231 + x * c; p = x * b / c; result = Math.Log(z) + p; return result; } q = (x - 0.5) * Math.Log(x) - x + ls2pi; if ((double)(x) > (double)(100000000)) { result = q; return result; } p = 1 / (x * x); if ((double)(x) >= (double)(1000.0)) { q = q + ((7.9365079365079365079365 * 0.0001 * p - 2.7777777777777777777778 * 0.001) * p + 0.0833333333333333333333) / x; } else { a = 8.11614167470508450300 * 0.0001; a = -(5.95061904284301438324 * 0.0001) + p * a; a = 7.93650340457716943945 * 0.0001 + p * a; a = -(2.77777777730099687205 * 0.001) + p * a; a = 8.33333333333331927722 * 0.01 + p * a; q = q + a / x; } result = q; return result; }

मेरी विधि

मेरी विधि निम्नलिखित कार्यों के अनुक्रम को लागू करना है:

हर में संख्याओं की डिग्री गिनें। उदाहरण के लिए, तर्क (5, 5, 5) के लिए वे होंगे: denomFactorPowers [6] = {0, 0, 2, 2, 2, 2}। यानी यदि हम हर भाज्य को गुणा करते हैं, तो हमें 3 ^ 2 * 4 ^ 2 * 5 ^ 2 * 6 ^ 2 मिलते हैं। और डिग्री ठीक दूसरी है, क्योंकि अंश का अंश अंश के साथ घट गया, और अंश में यह 1 * ... * 15 के बजाय 6 * ... * 15 हो गया।
प्रारंभिक परिणाम = 1 (फ़ंक्शन परिणाम); tempDenom = 1 (हर में संख्याओं को गुणा करने का परिणाम); currentFactor (हर में वर्तमान कारक)।
सभी शेष अंश संख्याओं पर चर i का चक्र (अधिकतम संख्या + 1 ... संख्यासम) ।
TempDenom का मूल्यांकन तक tempDenom < परिणाम और भाजक संख्याओं से बाहर चला गया है (currentFactor <denomFactorPowers.Length) ।
यदि tempDenom> परिणाम या संख्या भाजक (currentFactor> = denomFactorPowers.Length) में निकल गई है , तो परिणाम की गणना इस प्रकार करें: परिणाम = परिणाम / tempDenom * i । यह तकनीक आपको परिणाम को यथासंभव सटीक और बिना अतिप्रवाह के गणना करने की अनुमति देती है, क्योंकि परिणाम / tempDenom → 1 ।

मेरी विधि स्रोत

 public static ulong MyAr(uint[] numbers) { uint numbersSum = 0; foreach (var number in numbers) numbersSum += number; uint maxNumber = numbers.Max(); var denomFactorPowers = new uint[maxNumber + 1]; foreach (var number in numbers) for (int i = 2; i <= number; i++) denomFactorPowers[i]++; for (int i = 2; i < denomFactorPowers.Length; i++) denomFactorPowers[i]--; // reduce with nominator; uint currentFactor = 2; uint currentPower = 1; double result = 1; for (uint i = maxNumber + 1; i <= numbersSum; i++) { uint tempDenom = 1; while (tempDenom < result && currentFactor < denomFactorPowers.Length) { if (currentPower > denomFactorPowers[currentFactor]) { currentFactor++; currentPower = 1; } else { tempDenom *= currentFactor; currentPower++; } } result = result / tempDenom * i; } return (ulong)Math.Round(result); }

परीक्षण

सभी विधियों का परीक्षण दो चरणों में हुआ: यह अधिकतम संख्या के लिए एक परीक्षण है जिसे किसी भी विधि द्वारा अतिप्रवाह और गोलाई त्रुटियों के साथ-साथ गति परीक्षण के बिना गणना की जा सकती है।

उच्चतम संभव कम्प्यूटेबल संख्या के लिए परीक्षण करें

यह साबित करना आसान है कि एक बहुराष्ट्रीय गुणांक एक कम्यूटेटिव ऑपरेशन है, अर्थात्। उदा। एम। (ए, बी, सी) = एम (ए, सी, बी) = एम (सी, बी, ए), आदि। इसलिए, दी गई संख्या के तर्कों के साथ संख्याओं के सभी संयोजनों की जांच करने के लिए, आप पुनरावृत्ति के साथ क्रमपरिवर्तन का उपयोग कर सकते हैं। इन उद्देश्यों के लिए, कोडप्रोजेक्ट से डेटा और अन्य संयोजनों को उत्पन्न करने के लिए एक पुस्तकालय का उपयोग किया गया था। इस प्रकार, सभी संयोजनों को शाब्दिक क्रम में व्यवस्थित किया गया था।

नीचे दिए गए दो रेखांकन एक बहुराष्ट्रीय फ़ंक्शन में तर्कों की संख्या पर सबसे बड़ी संभावित कम्प्यूटेबल संख्या की क्रम संख्या की निर्भरता को दर्शाते हैं।

बेहतर समझ के लिए, मैं 2 तर्कों के साथ मूल्यों के पहले सेट की व्याख्या करूँगा:

 Arg count: 2 Naive(1,19) = 20; #18; overflow Binom(1,61) = 62; #60; overflow LogGamma(5,623) = 801096582000; #4612; rounding(error = 1) Log(6,588) = 59481941558292; #5572; rounding(error = 1) My(7,503) = 1708447057008120; #6481; rounding(error = 1) Big(8,959) = 18419736117819661560; #7930

यह ऊपर दिए गए परीक्षण में देखा जा सकता है, उदाहरण के लिए, लॉगरिथम का उपयोग करके गणना की जा सकने वाली अधिकतम ulong मान 59481941558292 है। यह तर्क 6 और 588 से गणना की गई थी, जो कि क्रमबद्ध 6481 से मेल खाती है यदि आप उन्हें लेक्सिकोग्राफ़िक क्रम में उत्पन्न करते हैं। यह संख्या ग्रीन ग्राफ पर प्रदर्शित होती है। गोलाई शब्द का अर्थ है कि यदि हम अगला क्रमांकन लेते हैं, अर्थात्। (६.५ method ९), तो यह विधि १. की त्रुटि के साथ बहुराष्ट्रीय गुणांक पर विचार करेगी और शब्द अतिप्रवाह का अर्थ है कि यदि हम गुणांक की गणना अगले क्रमांक से करते हैं (उदाहरण के लिए, अगर हम बिनोम के लिए (१.६३) लेते हैं, तो कहीं विधि के अंदर एक अतिप्रवाह होगा) ।

चूंकि पहली और अंतिम क्रमपरिवर्तन संख्या के बीच का अंतर बहुत बड़ा है, इसलिए मैंने ग्राफ़ को दो भागों में विभाजित किया (2-10 और 11-20 के तर्कों की संख्या के साथ)। इक्कीस या अधिक तर्कों पर, सभी कार्य पहले क्रमपरिवर्तन पर भी एक गलत परिणाम देते हैं (यह समझ में आता है, क्योंकि मल्टीमोनियल (1,1, ..., 1) = 21! और यह संख्या अधिकतम उछाल से अधिक है। किसी भी तर्क में और वृद्धि। केवल परिणाम बढ़ाएगा। मैं इस कथन को बिना प्रमाण के छोड़ दूंगा)।

नारंगी ग्राफ सही परिणाम दिखाता है, अर्थात आम तौर पर सबसे अधिक मैक्सिमम उलॉन्ग जो केवल एक बहुपदीय फ़ंक्शन द्वारा दिए गए तर्कों के साथ गणना की जा सकती है। यानी क्रमपरिवर्तन के एक और वृद्धि के कारण परिणाम उल्टी प्रकार से आगे निकल जाएगा । इस ग्राफ़ के मूल्यों की गणना बड़े पूर्णांक का उपयोग करके की गई थी, जिसकी चर्चा लेख की शुरुआत में की गई थी।

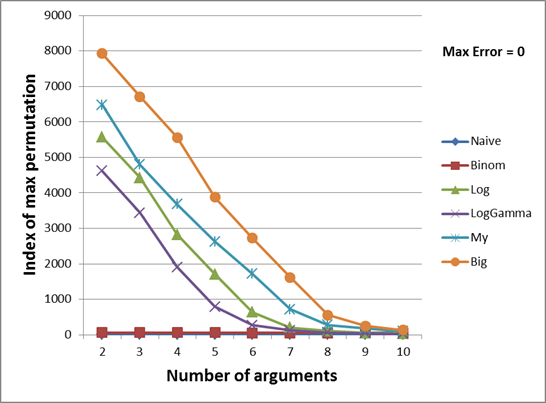
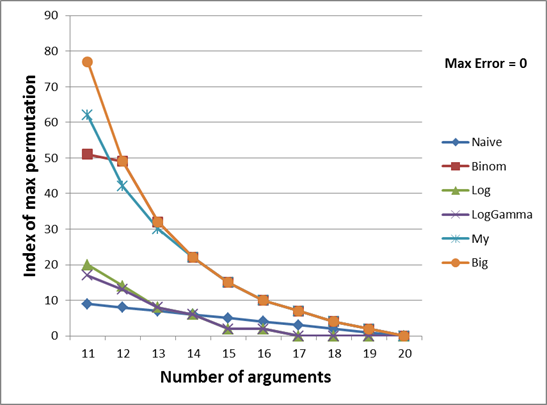
इसलिए, मेरी पद्धति, जैसा कि दोनों ग्राफ़ों से देखा जा सकता है, मुझे 12 और 13 तर्कों के अपवाद के साथ लगभग सभी मामलों में एक बड़ा गुणांक की गणना करने की अनुमति देता है। द्विपद गुणांक की उच्च अपेक्षाओं के बावजूद, यह पता चला कि वे छोटी संख्या (2 से 8 तक) के मामले में मूल्यों के एक छोटे समूह को कवर करते हैं। 9 से शुरू होने पर, वे लॉग और लॉगगम्मा की तुलना में एक बड़ी रेंज शुरू करते हैं, और 12 और 13 पर वे मेरी विधि को भी बायपास करते हैं। 13 के बाद, वे पूरी तरह से गणना करते हैं, हालांकि, जैसा कि वे मेरे तरीके से गणना करते हैं।

लॉग और लॉगगम्मा विधियां लगभग एक ही श्रेणी को कवर करती हैं, खासकर बड़ी संख्या में तर्कों के साथ। तथ्य यह है कि लॉग अभी भी लॉगगम्मा से 1-12 से आगे है शायद इस तथ्य के कारण है कि लॉग (एन!) फ़ंक्शन की गणना वास्तविक संख्या (लॉगरिथम) के योग से कम सटीक रूप से की जाती है। और एक साधारण विधि भी 15-19 संख्या के तर्कों के लिए लघुगणक की तुलना में अधिक प्रभावी साबित हुई।

यह ध्यान देने योग्य है कि जब मैक्स त्रुटि की पूर्ण त्रुटि (यानी, राउंडिंग के दौरान अधिकतम अनुमेय त्रुटि) बदल गई थी, तो तस्वीर बहुत नहीं बदली, इसलिए मैंने 10 और 100 की मैक्स त्रुटि के साथ अन्य ग्राफ़ नहीं दिए।

विधि प्रदर्शन परीक्षण

प्रत्येक विधि की गति को मापने के लिए, मैंने दो परीक्षण सेटों का उपयोग किया। पहला काफी बड़ी संख्या को कवर करता है, जिस पर सरल Naive विधि एक अतिप्रवाह त्रुटि के साथ दुर्घटनाग्रस्त हो जाती है, इसलिए इसे ध्यान में नहीं रखा गया था। बिगइंटर को भी नहीं गिना गया। प्रत्येक सेट को 20,000 बार चलाया गया था, और यह गणना समय मापा गया था।

इसके अलावा, इन तरीकों को प्रीफैच के साथ और बिना परीक्षण किया गया है। यह केवल लॉग और लॉगगम्मा विधियों के लिए प्रासंगिक है, क्योंकि केवल वे पूर्व- निर्धारित लॉगरिथम और फैक्टोरियल से लॉगरिथम का उपयोग करते हैं।

तर्कों का पहला परीक्षण सेट

 (1, 1) (1, 2) (2, 1) (2, 2) (5, 5, 5) (10, 10, 10) (5, 10, 15) (6, 6, 6, 6) (5, 6, 7, 8) (2, 3, 4, 5, 7)

जैसा कि आप देख सकते हैं, यहाँ मेरा तरीका अन्य विधियों की तुलना में 3 गुना खराब है।

तथ्य यह है कि बिनोम ने किसी और की तुलना में तेजी से सब कुछ की गणना की, इस तथ्य से समझाया गया है कि यह केवल पूर्णांक अंकगणितीय का उपयोग करता है, जो कि पहले से अधिक तेज है।

LogGamma की Log पर हल्की सी लीड को इस तथ्य से समझाया जाता है कि यह फिर से लघुगणक को जोड़ता नहीं है, लेकिन तुरंत तथ्य के लघुगणक को याद करता है, अर्थात उदाहरण के लिए, Ln (2) + Ln (3) + Ln (4) के बजाय Ln (4)! का उपयोग किया जाता है।

यह भी देखा गया है कि प्रीफ़ैच, जैसा कि यह निकला, लॉग और लॉगगम्मा की गति पर व्यावहारिक रूप से कोई प्रभाव नहीं पड़ता है, और इससे पता चलता है कि इन कार्यों की गणना जाहिरा तौर पर पहले से गणना किए गए मानों के निष्कर्षण के बराबर है या कि उनकी गणना का समय कुल की तुलना में बहुत कम है। शेष संचालन का समय।

तर्क का दूसरा टेस्ट सेट

निम्नलिखित सेट का उद्देश्य सरलतम अनुभवहीन कार्य के लिए भी था। निम्नलिखित आरेख में बड़ी संख्याओं को भी शामिल किया गया था:

 (1, 1) (1, 2) (2, 1) (2, 2) (5, 5, 5) (1, 1, 1, 1, 1, 1, 1, 1, 2) (1, 2, 3, 4, 5, 4)

जैसा कि आप देख सकते हैं, इस मामले में, मेरी विधि ने बाकी फ़ंक्शन ( बिग को छोड़कर) के साथ एक छोटा सा अंतर दिखाया, और बड़ी संख्या के साथ विधि मेरी विधि से भी 4 गुना खराब हो गई। ऐसा इसलिए है क्योंकि .NET में बड़ी संख्या का कार्यान्वयन आदर्श से बहुत दूर है। System.Numerics लाइब्रेरी के कुछ तरीकों को डिकॉन्फ़िलिंग करते हुए ILSpy के साथ मेरी मान्यताओं की पुष्टि हुई (कोड से पता चलता है कि इस तरह के सरल ऑपरेशन के लिए भी, बड़ी मात्रा में सुरक्षित कोड का उपयोग किया जाता है):

.NET में BigInteger के लिए ऑपरेशन जोड़ें

 public static BigInteger operator +(BigInteger left, BigInteger right) { if (right.IsZero) { return left; } if (left.IsZero) { return right; } int num = 1; int num2 = 1; BigIntegerBuilder bigIntegerBuilder = new BigIntegerBuilder(left, ref num); BigIntegerBuilder bigIntegerBuilder2 = new BigIntegerBuilder(right, ref num2); if (num == num2) { bigIntegerBuilder.Add(ref bigIntegerBuilder2); } else { bigIntegerBuilder.Sub(ref num, ref bigIntegerBuilder2); } return bigIntegerBuilder.GetInteger(num); } ... public void Add(ref BigIntegerBuilder reg) { if (reg._iuLast == 0) { this.Add(reg._uSmall); return; } if (this._iuLast != 0) { this.EnsureWritable(Math.Max(this._iuLast, reg._iuLast) + 1, 1); int num = reg._iuLast + 1; if (this._iuLast < reg._iuLast) { num = this._iuLast + 1; Array.Copy(reg._rgu, this._iuLast + 1, this._rgu, this._iuLast + 1, reg._iuLast - this._iuLast); this._iuLast = reg._iuLast; } uint num2 = 0u; for (int i = 0; i < num; i++) { num2 = BigIntegerBuilder.AddCarry(ref this._rgu[i], reg._rgu[i], num2); } if (num2 != 0u) { this.ApplyCarry(num); } return; } uint uSmall = this._uSmall; if (uSmall == 0u) { this = new BigIntegerBuilder(ref reg); return; } this.Load(ref reg, 1); this.Add(uSmall); }

निष्कर्ष

प्रयोगों से पता चला कि मेरी पद्धति अधिकतम संगणनीय संख्या (लेकिन अभी भी आदर्श एक से भी बदतर) के संदर्भ में दूसरों की तुलना में बेहतर है, लेकिन प्रदर्शन के संदर्भ में बदतर है (लेकिन साथ ही यह .NET में बड़ी संख्या के साथ कार्यान्वयन से बहुत बेहतर है)। हम यह भी निष्कर्ष निकाल सकते हैं कि बड़ी संख्या के अंकगणित का कार्यान्वयन .NET में आदर्श से बहुत दूर है और यदि इसे किसी अन्य विधि से प्रतिस्थापित करना संभव है, तो इसका उपयोग करना बेहतर है।

द्विपद गुणांक के साथ विधि एक सरल कार्यान्वयन की तुलना में सबसे तेज़, और भी तेज़ हो गई, लेकिन यह काफी स्पष्ट है, क्योंकि यह केवल पूर्णांक अंकगणित का उपयोग करता है। दूसरी ओर, यह विधि कई प्रकार के तर्कों को शामिल नहीं करती है, खासकर छोटी संख्या के तर्कों के साथ।

इसके अलावा, प्रयोगों से पता चला कि लघुगणकों के लघुगणकों और लघुगणकों के परिकलित मूल्यों का पुन: उपयोग करने से प्रदर्शन में कोई महत्वपूर्ण लाभ नहीं मिलता है, ताकि उन्हें छोड़ा जा सके।

मुझे उम्मीद है कि प्रयोगों के साथ किया गया काम न केवल मेरे लिए दिलचस्प और उपयोगी होगा, इसलिए मैं यूनिट कोड के साथ-साथ जीथब पर टेस्ट और टेस्ट के साथ स्रोत कोड पोस्ट करता हूं: मल्टीमिनोनल-गुणांक ।

अद्यतन

द्विपद गुणांक के साथ एक विधि अद्यतन: लिंक , लेखक: Mrrl
मुख्य संख्याओं की शक्तियों में अपघटन के साथ जोड़ा गया तरीका: लिंक , लेखक: Mrrl
योग की डिग्री का वर्णन : विवरण और स्रोत में विस्तार करके प्राप्त गुणांकों के संयोजन की गणना के साथ एक विधि जोड़ी गई है

बहुराष्ट्रीय गुणांक की गणना के लिए तरीके