विशेषता समारोह का दृश्य

कई रूपरेखाएँ बताती हैं कि किरण अनुरेखण कैसे काम करती है: आउटपुट विंडो में प्रत्येक पिक्सेल के माध्यम से, एल्गोरिथ्म बीम को पार करता है और गणना करता है कि दृश्य में कौन सी वस्तुएं इसे काटती हैं और परिणामस्वरूप पिक्सेल को कैसे रोशन किया जाना चाहिए। एल्गोरिथ्म को अनिवार्य रूप से यह आवश्यक है कि हमारे पास एक ऐसा फ़ंक्शन हो जो प्रत्येक स्थिति के लिए बिंदु का रंग लौटाए। बेशक, एक ही दृष्टिकोण को न केवल तीन आयामी ग्राफिक्स के लिए लागू किया जा सकता है: किसी भी छवि को इस तरह से रेखापुंज किया जा सकता है, अगर हमारे पास एक उपयुक्त फ़ंक्शन है। उदाहरण के लिए, साधारण फैक्टराइजेशन आरेखों की कल्पना करने की समस्या को हल करने के लिए इस दृष्टिकोण का उपयोग कैसे करें, इस पर विचार करें, जिसके बारे में हेलकार्स्क ने लिखा था ।

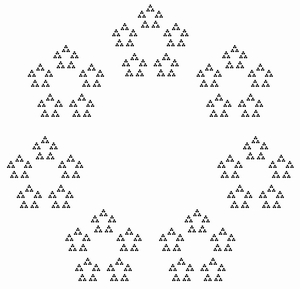
मेरा कार्यान्वयन यहाँ है । चित्र 10 दिखाता है! = 3628800, हालांकि सभी विवरण, निश्चित रूप से दिखाई नहीं दे रहे हैं।

इस समस्या में, जैसा कि कई अन्य लोगों में, रंग बिनाराइज़ किया जाता है: या तो काला या सफेद। तदनुसार, हमें फ़ंक्शन फ़ंक्शन चेक (x, y) के फ़ंक्शन की आवश्यकता है, जो एक तार्किक मान लौटाता है जो हमें बताता है कि दिए गए बिंदु को चित्रित करना है या नहीं। गणितज्ञ कहेंगे कि चेक (x, y) विमान पर बिंदुओं के सेट का एक विशिष्ट कार्य है (गणित में ऐसा फ़ंक्शन आमतौर पर 1 या 0 देता है)। यदि यह फ़ंक्शन निर्दिष्ट है, तो एचटीएमएल 5 कैनवस पर ड्राइंग एल्गोरिदम काफी सरल होगा:

function trace(canvas) { var ctx = canvas.getContext("2d"); var w = canvas.width; var h = canvas.height; var img = ctx.createImageData(w, h); for(var x=0; x<w; x++) for(var y=0; y<h; y++) if(check(x,y)) img.data[(y*w+x)*4+3]=255; ctx.putImageData(img, 0, 0); } 

यहाँ हम इस तथ्य का लाभ उठाते हैं कि createImageData एक काला पारदर्शी कैनवास बनाता है। हम केवल पारदर्शिता के लिए जिम्मेदार बाइट को बदलते हैं।

मान लें कि हम चित्रित करना चाहते हैं, उदाहरण के लिए, केंद्र (50, 50) और त्रिज्या 50 के साथ एक चक्र। चेक (x, y) फ़ंक्शन इस तरह दिखेगा:

 function check(x,y) { return (x-50)*(x-50)+(y-50)*(y-50)<50*50; } 

केंद्र से दूरी के वर्गों का योग त्रिज्या के वर्ग से कम है। हमें निम्न चित्र मिलते हैं:

बेशक, एक सर्कल के लिए, लाइब्रेरी फ़ंक्शन का उपयोग करना आसान और सस्ता है। इसके अलावा, हमारा सर्कल कोणीय हो गया। इसे थोड़ा दूर करने के लिए, हम उप-प्रस्तुतिकरण का उपयोग करते हैं: पिक्सेल को n × n छोटे वाले में विभाजित करें, उनमें से प्रत्येक के लिए चेक रन करें और सफल चेक की संख्या के अनुपात में पारदर्शिता सेट करें:

 function trace(canvas) { var ctx = canvas.getContext("2d"); var w = canvas.width; var h = canvas.height; var img = ctx.createImageData(w, h); var n = 2; for(var x=0; x<w; x++) for(var y=0; y<h; y++) { var k=0; for(var xx=0; xx<n; xx++) for(var yy=0; yy<n; yy++) if(check(x+xx/n, y+yy/n)) k++; if(k) img.data[(y*w+x)*4+3]=255*k/n/n; } ctx.putImageData(img, 0, 0); } 

परिणाम इस प्रकार है:

पहले से ही काफी खूबसूरत। कुछ के लिए, आप n का मान बढ़ा सकते हैं (निश्चित रूप से, यह गिनती करने के लिए धीमा होगा)।

आइए मूल समस्या पर वापस जाएं। अनिवार्य रूप से, हमें एक प्रधान कारक के आरेख के लिए एक विशेषता फ़ंक्शन लिखना होगा। मैं कार्य के सभी आवश्यक मापदंडों को पारित करने और पुनरावृत्ति का लाभ उठाने के लिए फ़ंक्शन प्रोटोटाइप को थोड़ा बदल दूंगा। चेक फ़ंक्शन तर्कों (कारकों, एन, एक्स, वाई, आर) को ले जाएगा, जहां एक्स और वाई सर्कल के केंद्र के सापेक्ष बिंदु के निर्देशांक हैं, आर सर्कल का त्रिज्या है, कारक प्रमुख कारकों का एक सरणी है, जहां दो को पहले से ही चौकों में संयोजित किया जाता है, जैसा कि हेलरक्ज्स्क ने किया था। और n सरणी का वह तत्व है जिसके साथ हमें विचार शुरू करने की आवश्यकता है। तब चेक फ़ंक्शन कुछ इस तरह दिखेगा:
- यदि केंद्र से वर्तमान बिंदु की दूरी त्रिज्या से अधिक है, तो बिंदु बिल्कुल फिट नहीं है - झूठे वापस;
- यदि सरणी के अंत के लिए n अंक, तो हम अंत तक पहुंच गए और आपको केवल एक भरा हुआ सर्कल खींचने की आवश्यकता है - हम सच लौट आएंगे;
- अन्यथा, हम अगले क्रम के सर्कल की त्रिज्या (आर 1) की गणना करते हैं;
- यदि केंद्र से वर्तमान बिंदु तक की दूरी त्रिज्या शून्य से कम है (2 * r1), तो बिंदु रिंग के अंदर गिरता है - झूठे वापस;
- उस क्षेत्र की गणना करें जिसमें बिंदु गिरता है (चित्र में ग्रे में);
- हम खुद को एक ही कारक, एक बड़ा n, एक नया त्रिज्या r1 और x और y मानों के साथ कॉल करते हैं, जिसे नए सर्कल के केंद्र के अनुसार समायोजित किया जाता है।

वह, वास्तव में, सब है। आप जेएस पर तैयार आवेदन को देख सकते हैं (ब्राउज़र में कैनवास समर्थन की आवश्यकता है, आईई 6-8 के लिए कोई फ़ॉलबैक नहीं है)। मैंने कारक के लिए हेलकार्स्क कार्यों का उपयोग किया, और प्रतिपादन पूरी तरह से मेरा है। मेरी तस्वीरें थोड़ी अलग हैं, क्योंकि मैंने हलकों की त्रिज्या और क्षेत्रों के स्थान की अलग-अलग गणना की है। आप देख सकते हैं कि रेंडरिंग गति व्यावहारिक रूप से इनपुट नंबर से स्वतंत्र है। हालांकि पहले सौ के लिए हेलरक्जस्क का कार्यान्वयन तेजी से होता है, लेकिन फिर मेरा जीतना शुरू हो जाता है (ईमानदारी के लिए, मैंने साइन और कॉशन के मूल्यों को कैश नहीं किया)। मेरे द्वारा उपयोग किया गया दृष्टिकोण मुझे कई गैर-तुच्छ चीजों के दृश्य को सरल बनाने और गति प्रदान करने की अनुमति देता है। भग्न का प्रतिपादन करते समय यह विशेष रूप से उपयोगी होता है। ध्यान दें कि मेरे दृष्टिकोण से चित्र के किसी भी क्षेत्र में असीमित ज़ूम जोड़ना बहुत आसान है।