👋🏼 👍🏻 📼 सी # में सॉफ्टमैक्स परत के साथ तंत्रिका नेटवर्क 🙉 ⚱️ 🤘

नमस्ते, पिछले लेख में मैंने त्रुटि के प्रचार के लिए एल्गोरिथम के बारे में बात की और एक कार्यान्वयन लाया जो त्रुटि फ़ंक्शन और न्यूरॉन के सक्रियण फ़ंक्शन से स्वतंत्र है। इन समान मापदंडों के प्रतिस्थापन के कई सरल उदाहरण दिखाए गए थे: यूक्लिडियन वर्ग का न्यूनतमकरण और सिग्मोइड फ़ंक्शन और हाइपरबोलिक स्पर्शरेखा के लिए लघुगणकीय संभावना। यह पोस्ट अतीत की एक तार्किक निरंतरता होगी, जिसमें मैं क्रॉस-एंट्रोपी को कम करने के लिए थोड़ा गैर-मानक उदाहरण, अर्थात् सॉफ्टमैक्स सक्रियण फ़ंक्शन पर विचार करूंगा । यह मॉडल वर्गीकरण समस्या के लिए प्रासंगिक है, जब तंत्रिका नेटवर्क के उत्पादन में प्राप्त करना आवश्यक होता है, तो इनपुट छवि गैर-अंतर-वर्ग वर्गों में से एक से संबंधित होती है। जाहिर है, आउटपुट परत के सभी न्यूरॉन्स के लिए कुल नेटवर्क आउटपुट एक के बराबर होना चाहिए (साथ ही प्रशिक्षण नमूने की आउटपुट छवियों के लिए)। हालांकि, यह केवल आउटपुट को सामान्य करने के लिए पर्याप्त नहीं है, लेकिन आपको नेटवर्क को संभाव्यता वितरण का अनुकरण करने की आवश्यकता है, और इसे बस सिखाएं। वैसे, वर्तमान में तंत्रिका नेटवर्क पर एक कोर्स coursera.org पर हो रहा है , यह वह था जिसने सॉफ्टमैक्स की समझ में देरी करने में मदद की, अन्यथा मैं तीसरे पक्ष के कार्यान्वयन का उपयोग करना जारी रखूंगा।

का उपयोग करते हुए

मेरा सुझाव है कि आप अपने आप को पिछली पोस्ट के साथ परिचित करें, क्योंकि सभी संकेतन, इंटरफेस और लर्निंग एल्गोरिदम का उपयोग यहां परिवर्तनों के बिना किया जाता है।

सॉफ्टमैक्स एक्टिवेशन फंक्शन

इसलिए, पहला कार्य जो हमें सामना करता है वह है नेटवर्क को संभाव्यता वितरण को मॉडल करने का एक तरीका प्रदान करना। ऐसा करने के लिए, एक प्रत्यक्ष वितरण नेटवर्क बनाएं जैसे:

नेटवर्क में कई छिपी हुई परतें होती हैं, सभी न्यूरॉन्स का अपना सक्रियण कार्य हो सकता है;
अंतिम परत पर न्यूरॉन्स की एक ऐसी संख्या होती है जो कक्षाओं की संख्या से मेल खाती है; इन सभी न्यूरॉन्स को सॉफ्टमैक्स परत या समूह कहा जाएगा।

सॉफ्टमैक्स-समूह के न्यूरॉन्स में निम्नलिखित सक्रियण समारोह होगा (इस खंड में मैं परत सूचकांक को छोड़ दूंगा, यह निहित है कि यह अंतिम है और इसमें एन न्यूरॉन्स शामिल हैं):

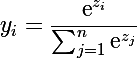i-th न्यूरॉन के लिए

यह सूत्र से देखा जा सकता है कि प्रत्येक न्यूरॉन का उत्पादन सॉफ्टमैक्स समूह के अन्य सभी न्यूरॉन्स के जोड़ पर निर्भर करता है, और पूरे समूह के आउटपुट मानों का योग एकता है। इस फ़ंक्शन की सुंदरता यह है कि इसके योजक में i-th न्यूरॉन का आंशिक व्युत्पन्न बराबर है:

हम पिछले लेख से IF इंटरफ़ेस का उपयोग करके इस फ़ंक्शन को लागू करते हैं:

सॉफ्टमैक्स फ़ंक्शंस लागू करें

यह ध्यान देने योग्य है कि double Compute(double x) विधि का कार्यान्वयन आमतौर पर आवश्यक नहीं है, क्योंकि सॉफ्टमैक्स परत के कार्यान्वयन में समूह के आउटपुट मूल्यों की गणना करना सस्ता होगा। लेकिन पूर्णता के लिए, और सिर्फ मामले में, इसे रहने दो)

 internal class SoftMaxActivationFunction : IFunction { private ILayer _layer = null; private int _ownPosition = 0; internal SoftMaxActivationFunction(ILayer layer, int ownPosition) { _layer = layer; _ownPosition = ownPosition; } public double Compute(double x) { double numerator = Math.Exp(x); double denominator = numerator; for (int i = 0; i < _layer.Neurons.Length; i++) { if (i == _ownPosition) { continue; } denominator += Math.Exp(_layer.Neurons[i].LastNET); } return numerator/denominator; } public double ComputeFirstDerivative(double x) { double y = Compute(x); return y*(1 - y); } public double ComputeSecondDerivative(double x) { throw new NotImplementedException(); } }

त्रुटि समारोह

प्रत्येक प्रशिक्षण उदाहरण में, हम एक नेटवर्क आउटपुट प्राप्त करेंगे जो कि संभाव्यता वितरण को मॉडल करता है, और दो प्रायिकता वितरण की तुलना करने के लिए एक सही माप की आवश्यकता होती है। इस तरह के उपाय के रूप में क्रॉस एन्ट्रापी का उपयोग किया जाएगा:

टी - वर्तमान प्रशिक्षण उदाहरण के लिए आवश्यक आउटपुट
वाई - तंत्रिका नेटवर्क के वास्तविक आउटपुट

एक सामान्य नेटवर्क त्रुटि की गणना इस प्रकार की जाती है:

पूरे मॉडल की भव्यता का एहसास करने के लिए, आपको यह देखने की ज़रूरत है कि कैसे ग्रेडिएंट की गणना आउटपुट आयामों या न्यूरॉन में से एक से की जाती है। "आउटपुट लेयर" अनुभाग में पिछली पोस्ट में, यह वर्णन किया गया है कि कार्य dC / dz_i की गणना करने के लिए कम है, हम अभी से जारी रखेंगे:

क्योंकि प्रत्येक न्यूरॉन के आउटपुट में करंट का योजक होता है, हमें पूरी राशि को अलग करना होगा। इस तथ्य के कारण कि लागत फ़ंक्शन केवल न्यूरॉन्स के आउटपुट पर निर्भर करता है, और केवल एडरों पर आउटपुट, यह दो आंशिक डेरिवेटिव में विघटित हो सकता है। इसके बाद, हम व्यक्तिगत रूप से राशि के प्रत्येक सदस्य पर विचार करेंगे (मुख्य बात सूचकांकों पर ध्यान देना है, हमारे मामले में समूह के सॉफ्टमैक्स न्यूरॉन्स के माध्यम से चलता है, और मैं वर्तमान न्यूरॉन है)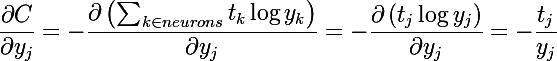

अंतिम परिवर्तन इस तथ्य के कारण प्राप्त होता है कि सॉफ्टमैक्स समूह के न्यूरॉन्स की संपत्ति के अनुसार आउटपुट वेक्टर के मूल्यों का योग एकता के बराबर होना चाहिए। प्रशिक्षण नमूने के लिए यह एक महत्वपूर्ण आवश्यकता है, अन्यथा ग्रेडिएंट की सही गणना नहीं की जाएगी!

हम पहले के समान प्रतिनिधित्व का उपयोग करके कार्यान्वयन के लिए आगे बढ़ते हैं:

क्रॉस एंट्रॉपी कार्यान्वयन

 internal class CrossEntropy : IMetrics<double> { internal CrossEntropy() { } /// <summary> /// \sum_i v1_i * ln(v2_i) /// </summary> public override double Calculate(double[] v1, double[] v2) { double d = 0; for (int i = 0; i < v1.Length; i++) { d += v1[i]*Math.Log(v2[i]); } return -d; } public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index) { return v2[v2Index] - v1[v2Index]; } }

सॉफ्टमैक्स परत

सामान्यतया, आपको एक विशेष परत बनाने की आवश्यकता नहीं है, बस ऊपर दिखाए गए सक्रियण फ़ंक्शन के साथ एक साधारण प्रत्यक्ष वितरण नेटवर्क के निर्माता में अंतिम परत बनाएं और निर्माणकर्ता को सॉफ्टमैक्स परत के लिए एक लिंक पास करें, लेकिन तब फ़ंक्शन के हर की गणना प्रत्येक न्यूरॉन के आउटपुट की गणना करते समय की जाएगी। सक्रियण, लेकिन यदि आप तंत्रिका नेटवर्क के double[] ComputeOutput(double[] inputVector) ठीक से लागू करते हैं:

 public double[] ComputeOutput(double[] inputVector) { double[] outputVector = inputVector; for (int i = 0; i < _layers.Length; i++) { outputVector = _layers[i].Compute(outputVector); } return outputVector; }

फिर, क्योंकि नेटवर्क सीधे न्यूरॉन की गणना विधि को कॉल नहीं करता है, लेकिन इस फ़ंक्शन को परत में दर्शाता है, एक बार गणना की गई सक्रियण फ़ंक्शन के हर को बनाना संभव है।

सॉफ्टमैक्स परत

 internal class SoftmaxFullConnectedLayer : FullConnectedLayer { internal SoftmaxFullConnectedLayer(int inputDimension, int size) { _neurons = new INeuron[size]; for (int i = 0; i < size; i++) { IFunction smFunction = new SoftMaxActivationFunction(this, i); _neurons[i] = new InLayerFullConnectedNeuron(inputDimension, smFunction); } } public override double[] Compute(double[] inputVector) { double[] numerators = new double[_neurons.Length]; double denominator = 0; for (int i = 0; i < _neurons.Length; i++) { numerators[i] = Math.Exp(_neurons[i].NET(inputVector)); denominator += numerators[i]; } double[] output = new double[_neurons.Length]; for (int i = 0; i < _neurons.Length; i++) { output[i] = numerators[i]/denominator; _neurons[i].LastState = output[i]; } return output; } }

परिणाम

तो, लापता हिस्से तैयार हैं, और आप कंस्ट्रक्टर को इकट्ठा कर सकते हैं। उदाहरण के लिए, मैं एक ही सीधे वितरण नेटवर्क कार्यान्वयन का उपयोग करता हूं, बस एक अलग निर्माता के साथ ।

कंस्ट्रक्टर उदाहरण

 /// <summary> /// Creates network with softmax layer at the outlut, and hidden layes with theirs own activation functions /// </summary> internal FcMlFfNetwork(int inputDimension, int outputDimension, int[] hiddenLayerStructure, IFunction[] hiddenLayerFunctions, IWeightInitializer wi, ILearningStrategy<IMultilayerNeuralNetwork> trainingAlgorithm) { _learningStrategy = trainingAlgorithm; _layers = new ILayer[hiddenLayerFunctions.Length + 1]; _layers[0] = new FullConnectedLayer(inputDimension, hiddenLayerStructure[0], hiddenLayerFunctions[0]); for (int i = 1; i < hiddenLayerStructure.Length; i++) { _layers[i] = new FullConnectedLayer(_layers[i - 1].Neurons.Length, hiddenLayerStructure[i], hiddenLayerFunctions[i]); } //create softmax layer _layers[hiddenLayerStructure.Length] = new SoftmaxFullConnectedLayer(hiddenLayerStructure[hiddenLayerStructure.Length - 1], outputDimension); for (int i = 0; i < _layers.Length; i++) { for (int j = 0; j < _layers[i].Neurons.Length; j++) { _layers[i].Neurons[j].Bias = wi.GetWeight(); for (int k = 0; k < _layers[i].Neurons[j].Weights.Length; k++) { _layers[i].Neurons[j].Weights[k] = wi.GetWeight(); } } } }

सी # में सॉफ्टमैक्स परत के साथ तंत्रिका नेटवर्क

का उपयोग करते हुए

सॉफ्टमैक्स एक्टिवेशन फंक्शन

त्रुटि समारोह

सॉफ्टमैक्स परत

परिणाम

More articles: