📆 🌡️ 👩🏾‍💼 पारदर्शिता बनाम सतह अभिविन्यास 🌾 🚑 🚤

दूसरे दिन, मेरे हाथों में प्लास्टिक के कप को घुमाते हुए, मैंने देखा कि प्लास्टिक की दृश्यता पारदर्शिता उस कोण पर निर्भर करती है जिस पर आप सतह को देखते हैं - यदि आप सतह के लंबवत दिखते हैं, तो पृष्ठभूमि स्पष्ट रूप से दिखाई देती है, और यदि आप सतह के साथ देखते हैं, तो सामग्री लगभग बन जाती है। अपारदर्शी। इस घटना ने मुझे दिलचस्पी दी, और मैंने एक गणितीय मॉडल बनाने का फैसला किया।

जल्दी से नहीं कहा। कटआउट के तहत, सूत्र आउटपुट, टुकड़ा shader कोड और एक छोटा डेमो।

हम मानते हैं कि सामग्री ऑप्टिकल सजातीय है - इसके ऑप्टिकल गुण दिशा से स्वतंत्र हैं। फिर पारदर्शिता में परिवर्तन सामग्री की मोटाई में प्रकाश किरण के विभिन्न पथ लंबाई के कारण होता है।

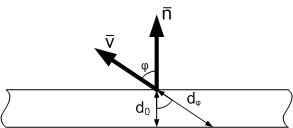
$d_\varphi = \frac{d_0}{\cos \varphi},\cos \varphi = \vec{n} \cdot \vec{v}$ जहाँ $\vec{n}$ सतह के लिए इकाई सामान्य वेक्टर है, $\vec{v}$ क्या प्रेक्षक के लिए यूनिट दिशा वेक्टर है।

सामग्री की स्पष्ट पारदर्शिता को अस्पष्टता गुणांक द्वारा निर्धारित किया जाता है, जो पृष्ठभूमि के रंग के साथ सामग्री के रंग के मिश्रण को निर्धारित करता है: $C_\texttt{visible} = \alpha C_\texttt{material} + (1 - \alpha)C_\texttt{background}$

आइए देखें कि कैसे मूल्य $\alpha$ सामग्री की मोटाई पर निर्भर करता है। ऐसा करने के लिए, सामग्री की परत को मोटाई के साथ तोड़ दें $d_0$ और अस्पष्टता $\alpha_0$ पर $N$ एक ही मोटाई की परतें $d_\varepsilon$ एक अस्पष्टता कारक के साथ प्रत्येक $\alpha_\varepsilon$ । चलो $C_0$ - पृष्ठभूमि रंग $C_m$ - सामग्री का रंग, और $C_i,i=1...N$ - प्रत्येक परत के आउटपुट पर रंग।

$C_1=\alpha_\varepsilon C_m+(1-\alpha_\varepsilon)C_0 \par C_2=\alpha_\varepsilon C_m+(1-\alpha_\varepsilon)C_1 = \alpha_\varepsilon C_m+(1-\alpha_\varepsilon)[\alpha_\varepsilon C_m+(1-\alpha_\varepsilon)C_0] = \par = (2\alpha_\varepsilon - \alpha_\varepsilon^2)C_m + (1-\alpha_\varepsilon)^2 C_0 = (1-(1 - \alpha_\varepsilon)^2) C_m+(1-\alpha_\varepsilon)^2 C_0 \par C_3=\alpha_\varepsilon C_m+(1-\alpha_\varepsilon)C_2 = \alpha_\varepsilon C_m+(1-\alpha_\varepsilon)[(1-(1 - \alpha_\varepsilon)^2) C_m+(1-\alpha_\varepsilon)^2 C_0] = \par = (\alpha_\varepsilon + 1 - \alpha_\varepsilon + (1 - \alpha_\varepsilon)^3)C_m + (1-\alpha_\varepsilon)^3 C_0 = (1-(1 - \alpha_\varepsilon)^3) C_m+(1-\alpha_\varepsilon)^3 C_0 \par ... \par C_N= (1-(1 - \alpha_\varepsilon)^N) C_m+(1-\alpha_\varepsilon)^N C_0$

लेकिन यह भी $C_N=\alpha_0 C_m+(1-\alpha_0)C_0$ और इसलिए:

यानी बढ़ती मोटाई के साथ, सामग्री की स्पष्ट पारदर्शिता तेजी से घट जाती है।

मोटाई दें $d_\varphi=kd_\varepsilon$ तब:
$1 - \alpha_\varphi = (1-\alpha_\varepsilon)^k=(1-\alpha_\varepsilon)^\frac{d_\varphi}{d_\varepsilon}=(1-\alpha_0)^{\frac{d_\varepsilon}{d}\times \frac{d_\varphi}{d_\varepsilon}}=(1-\alpha_0)^\frac{d_\varphi}{d_0}=(1-\alpha_0)^\frac{1}{\cos \varphi}$

तो, वांछित सूत्र: ${\color{Blue} \alpha(\varphi) = 1 - (1 - \alpha_0)^\frac{1}{\cos \varphi}}$

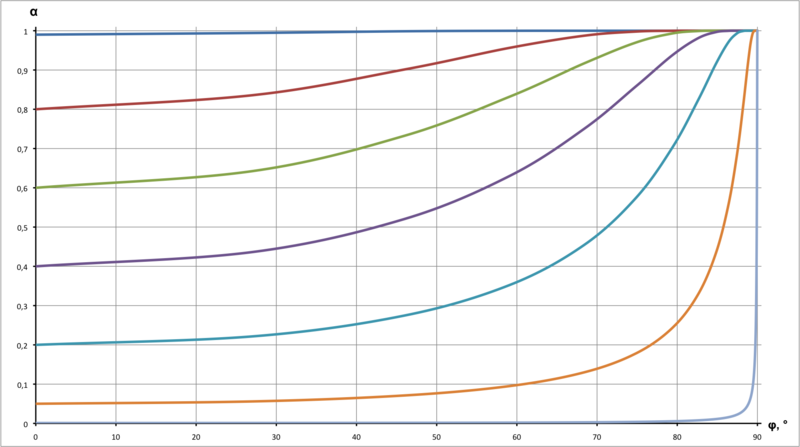
नीचे उस टुकड़े के लिए कोड है जो इस सूत्र को लागू करता है:

varying vec4 v_color; varying vec3 v_normal; varying vec3 v_eye; void main(void) { //         float cosPhi = dot(v_normal, v_eye) / sqrt( dot(v_normal, v_normal) * dot(v_eye, v_eye) ); //    ,        //     ,      // 0.999 ^ 10000 = 4.5173346E-5 float alpha = 1.0 - pow(1.0 - v_color.a, 1.0 / max(abs(cosPhi), 0.00001)); gl_FragColor = vec4(vec3(v_color), alpha); };

परिणाम यह है:

डेमो स्रोत कोड bitbucket.org पर उपलब्ध है

पारदर्शिता बनाम सतह अभिविन्यास

More articles: