जंप पॉइंट सर्च पाथ एलगोरिदम

यह एल्गोरिथ्म एक बेहतर ए * पथ खोज एल्गोरिथ्म है । JPS कई स्थानों को "कूद" करके पथ की खोज को गति देता है जिन्हें देखा जाना चाहिए। समान एल्गोरिदम के विपरीत, जेपीएस को पूर्व-प्रसंस्करण और अतिरिक्त मेमोरी लागतों की आवश्यकता नहीं है। यह एल्गोरिदम 2011 में पेश किया गया था, और 2012 में उच्च प्रतिक्रियाएं मिलीं । यह एल्गोरिथम क्या है और इसके कार्यान्वयन को लेख में आगे पढ़ा जा सकता है।

शब्दावली और संकेतन

एल्गोरिथ्म एकल मान के अप्रत्यक्ष ग्राफ पर काम करता है। प्रत्येक मानचित्र फ़ील्ड में <= 8 पड़ोसी हैं जो चलने योग्य हो सकते हैं या नहीं। दिशा में प्रत्येक कदम (लंबवत या क्षैतिज रूप से) की लागत 1 है; विकर्ण कदम की लागत agon2 है। बाधाओं के माध्यम से आंदोलन निषिद्ध है। पदनाम आंदोलन की आठ दिशाओं (ऊपर, नीचे, बाएं, आदि) में से एक को संदर्भित करता है।

• Y = x + kd लिखने का अर्थ है कि बिंदु y को x से दिशा में k चरणों में पहुँचा जा सकता है d। जब डी विकर्ण आंदोलन होता है, तो आंदोलन को एक सीधी रेखा डी ₁ और डी ₂ में दो आंदोलनों में विभाजित किया जाता है।
• पथ p = (n ₀ , n ₁ , ..., n _k ) बिंदु n ₀ से बिंदु _k तक के चक्र के बिना बिंदुओं के साथ एक क्रमबद्ध गति है।
• नोटेशन p \ x का अर्थ है कि पथ x पर बिंदु x उत्पन्न नहीं होता है।
• पदनाम लेन (पी) का अर्थ है पथ पी की लंबाई या लागत।
• पदनाम dist (x, y) का अर्थ है बिंदु x और y के बीच के मार्ग की लंबाई या लागत।

कूदो अंक

"जंपिंग पॉइंट्स" आपको केवल "आवश्यक" बिंदुओं पर विचार करते हुए पथ खोज एल्गोरिथ्म को गति देने की अनुमति देता है। इस तरह के बिंदुओं को एक पुनरावर्ती खोज में पड़ोसियों के चयन के लिए दो सरल नियमों द्वारा वर्णित किया जा सकता है: एक नियम आयताकार गति के लिए और दूसरा विकर्ण गति के लिए। दोनों मामलों में, यह साबित करना आवश्यक है कि, बिंदु के आसपास के निकटतम पड़ोसियों के सेट को छोड़कर, वर्तमान बिंदु के पूर्वज से प्रत्येक पड़ोसी के लिए एक इष्टतम मार्ग है, और इस पथ में विज़िट किए गए बिंदु नहीं होंगे। केस 1 पर विचार करें, जो मुख्य विचार को दर्शाता है:

केस 1 : एक कट ऑफ नेबर



X प्रश्न में वर्तमान बिंदु है। तीर यात्रा की दिशा को इंगित करता है। वहाँ और वहाँ दोनों आप तुरंत ग्रे में हाइलाइट किए गए पड़ोसियों को काट सकते हैं, क्योंकि पी (एक्स) से इष्टतम पथ के साथ कोई भी वहां पहुंच सकता है, एक्स के माध्यम से कभी नहीं गुजरता।

हम उन बिंदुओं के समूह को संदर्भित करेंगे जो वर्तमान बिंदु के वास्तविक पड़ोसियों को काटने के बाद बने रहें। वे आंकड़े में सफेद रंग में चिह्नित हैं। आदर्श रूप में, हम देखने पर केवल वास्तविक पड़ोसियों पर विचार करना चाहते हैं। हालांकि, कुछ मामलों में, बाधाओं की उपस्थिति का मतलब हो सकता है कि हमें K अतिरिक्त बिंदुओं (0) K ≤ 2) तक के एक छोटे सेट पर भी विचार करना चाहिए। हम कहते हैं कि ये मौजूदा स्थिति के मजबूर पड़ोसियों के बिंदु हैं।

केस 2 : जबरन पड़ोसी

X प्रश्न में वर्तमान बिंदु है। तीर यात्रा की दिशा को इंगित करता है। ध्यान दें कि जब x एक बाधा के पास होता है, तो चयनित पड़ोसियों को नहीं काटा जा सकता है, इन नोड्स में से प्रत्येक पर p (x) से कोई भी वैकल्पिक इष्टतम पथ अवरुद्ध है।

इन मामलों को निम्नानुसार लागू किया जाता है: "मजबूर" और "प्राकृतिक" पड़ोसियों को बनाने के बजाय, हम प्रत्येक बिंदु के आसपास पड़ोसियों की सूची को पुन: काट देते हैं। इस प्रकार, हमारा लक्ष्य उन सभी बिंदुओं के माध्यम से "जंपिंग" द्वारा "समरूपता" को खत्म करना है जो कि वर्तमान पथ से गुजरने वाले इष्टतम पथ के साथ पहुंचा जा सकता है। किसी बाधा से टकराने पर पुनरावृत्ति रुक ​​जाती है या तथाकथित "जंप पॉइंट उत्तराधिकारी" (जंप पॉइंट उत्तराधिकारी) मिल जाता है। जंपिंग पॉइंट्स दिलचस्प हैं कि उनके पास पड़ोसी हैं जो वैकल्पिक तरीके से नहीं पहुंच सकते हैं: इष्टतम पथ को वर्तमान बिंदु से गुजरना चाहिए। इस प्रकार g (y) = g (x) + dist (x; y) हिलने की लागत है।

अनुकूलता सुनिश्चित करने के लिए, केवल यह निर्धारित करना आवश्यक है कि पड़ोसी कैसे चुनें (पहले रैखिक, फिर विकर्ण)।

एक उदाहरण पर विचार करें:



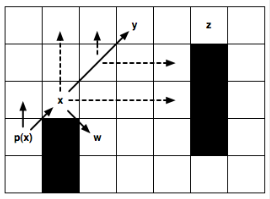
यहां हम विचार के लिए बिंदु x जोड़ते हैं, जिसका पूर्वज p (x) है; पी (एक्स) से एक्स तक की दिशा दाईं ओर एक सुधारा आंदोलन है।

(बाएं चित्र): कटऑफ नियम को पुन: लागू करें और जंपिंग पॉइंट x के उत्तराधिकारी के रूप में y प्राप्त करें। यह बिंदु दिलचस्प है क्योंकि एक पड़ोसी z है, जिसे केवल y के माध्यम से इष्टतम पथ तक पहुँचा जा सकता है। मध्यवर्ती अंक उत्पन्न नहीं होते हैं और विचार नहीं किए जाते हैं।

(सही तस्वीर): विकर्ण कटऑफ नियमों को पुन: स्वीकार करें। कृपया ध्यान दें कि प्रत्येक अगले विकर्ण कदम से पहले, आपको पुन: सीधी रेखाओं (एक धराशायी रेखा द्वारा इंगित) के साथ चलना चाहिए। केवल अगर दोनों "प्रत्यक्ष" पुनरावर्ती अगली छलांग के बिंदु को निर्धारित नहीं कर सकते हैं, तो हम विकर्ण के साथ आगे बढ़ते हैं। प्वाइंट डब्ल्यू - मजबूर पड़ोसी एक्स, हमेशा की तरह बनाया गया है।

पड़ोसी कतरन नियम

इसके बाद, हम वर्णन करते हैं कि किसी बिंदु x से सीधे सटे बिंदुओं के सेट को कैसे काटें। लक्ष्य ऐसे पड़ोसियों को ढूंढना है, अर्थात्। पड़ोसी (x ), किसी भी ऐसे n अंक तक, जिसका लक्ष्य तक पहुंचना असंभव है। हम इसे दो रास्तों की तुलना करके प्राप्त करते हैं: p, जो p (x) से शुरू होता है, x पर जाता है और cn से समाप्त होता है, और दूसरा रास्ता p ', जो p (x) से शुरू होता है, x पर जाता है और n से समाप्त होता है, लेकिन इसमें x नहीं होता है। इसके अलावा, p या p 'में निहित प्रत्येक बिंदु को पड़ोसियों (x ) को संदर्भित करना चाहिए।

दो मामले हैं, जिसके आधार पर x से संक्रमण p (x) से होता है: एक सीधी चाल या एक विकर्ण चाल। यह विचार करने योग्य है कि यदि x, p (x) की शुरुआत है, तो p (x) खाली है और क्लिपिंग नहीं होती है।

प्रत्यक्ष संक्रमण:

किसी भी बिंदु काट दिया जाता है जो निम्नलिखित कथन को पूरा करता है:
(1)
और
यहाँ p (x) = 4 और हमने n = 5 को छोड़कर सभी पड़ोसियों को काट दिया

विकर्ण संक्रमण:

यहां अंतर यह है कि एक्स को बाहर करने वाला मार्ग सख्ती से प्रभावी होना चाहिए:

(2)
ख
यहाँ p (x) = 6 और सभी पड़ोसियों को काट दिया जाता है, n = 2, n = 3 और n = 5 को छोड़कर।

यह मानते हुए कि पड़ोसियों (x) में बाधाएं नहीं हैं, हम उन बिंदुओं को संदर्भित करेंगे जो x के प्राकृतिक पड़ोसियों के रूप में प्रत्यक्ष या विकर्ण कट-ऑफ (यदि आवश्यक हो) के बाद बने रहें। वे ए और बी आंकड़ों में गैर-ग्रे डॉट्स के अनुरूप हैं। जब पड़ोसियों (x) में बाधाएं आती हैं, तो आप सभी गैर-प्राकृतिक पड़ोसियों को काट नहीं सकते। इस मामले में, ऐसे पड़ोसी को मजबूर (कृत्रिम) माना जाता है।

परिभाषा १।

बिंदु मजबूर है अगर



में
उदाहरण एक प्रत्यक्ष संक्रमण दिखाता है, जहां n = 3 मजबूर है।

जी
उदाहरण डी विकर्ण आंदोलन का एक उदाहरण दिखाता है; यहाँ n = 1 एक मजबूर पड़ोसी है।

एल्गोरिथम विवरण

हम परिभाषा प्रस्तुत करते हैं:

परिभाषा २।

बिंदु y, d दिशा में, बिंदु x का छलांग बिंदु है, यदि y k का मान कम से कम करता है ताकि y = x + kd, और निम्न में से एक स्थिति सत्य हो:

1. बिंदु y गंतव्य है।
2. बिंदु y में कम से कम एक पड़ोसी है जिसे परिभाषा 1 द्वारा मजबूर किया गया है।
3. डी विकर्ण आंदोलन है और एक बिंदु है z = y + k _i d _i ,   जो कि k _i दिशा में d _i 1 {d1, d2} में स्थित है, जैसे कि z, 1 या 2 की अवस्था में y से जंप पॉइंट है।

यह आंकड़ा एक जंपिंग पॉइंट का उदाहरण दिखाता है, जिसे कंडीशन 3 से परिभाषित किया जाता है। यहां हम बिंदु x पर शुरू करते हैं और जब तक हम बिंदु y से नहीं टकराते हैं, तब तक आन्दोलन को समाप्त कर देते हैं। Y से बिंदु z तक आप k _i क्षैतिज चरणों के साथ प्राप्त कर सकते हैं। इस प्रकार, z जंप पॉइंट x (स्थिति 2 से) का उत्तराधिकारी है, और यह बदले में y को जंप पॉइंट x के उत्तराधिकारी के रूप में परिभाषित करता है।

एल्गोरिथम 1 । उत्तराधिकारी की परिभाषा।

चलो सेट करें: x - वर्तमान बिंदु, एस - शुरुआत, जी - लक्ष्य



एल्गोरिथम 1 दिखाता है कि वर्तमान बिंदु के लिए एक उत्तराधिकारी की खोज कैसे की जाए। सबसे पहले, पड़ोसियों का सेट काट दिया जाता है, तुरंत वर्तमान बिंदु x (पंक्ति 2) से सटे। फिर, एक्स के लिए उत्तराधिकारियों (उत्तराधिकारियों) के सेट में प्रत्येक पड़ोसी एन को जोड़ने के बजाय, एक ऐसे बिंदु पर "कूद" करने की कोशिश करें जो आगे दूर है, लेकिन जो दिशा x से n के सापेक्ष स्थित है (लाइनें 3-5)। उदाहरण के लिए, यदि धार (x; n) x के दाईं ओर एक सीधी रेखा की चाल है, तो हम सीधे x के दाईं ओर कूद बिंदु को देखते हैं। यदि ऐसा कोई बिंदु पाया जाता है, तो इसे n के बजाय उत्तराधिकारियों के सेट में जोड़ा जाता है। यदि आप जम्प पॉइंट तक नहीं पहुँच सकते हैं, तो कुछ भी नहीं जोड़ा जाता है। प्रक्रिया तब तक जारी रहती है जब तक सभी पड़ोसी समाप्त नहीं हो जाते हैं, और फिर एल्गोरिथ्म x (पंक्ति 6) के लिए सभी उत्तराधिकारियों की एक सूची देता है।

एल्गोरिथम 2 । कूद समारोह।

चलो सेट करें: x - रिपोर्टिंग बिंदु, डी - दिशा, एस - शुरुआत, जी - लक्ष्य



जंप पॉइंट के लिए अलग-अलग उत्तराधिकारियों को खोजने के लिए, हम एल्गोरिथम 2 का उपयोग करते हैं। इसके लिए रिपोर्टिंग बिंदु x, आंदोलन की दिशा d, साथ ही शुरुआती बिंदु s और लक्ष्य बिंदु g की आवश्यकता होती है। एल्गोरिदम यह निर्धारित करने की कोशिश करता है कि क्या x उत्तराधिकारियों के बीच कूद बिंदु है, डी दिशा (लाइन 1) में घूम रहा है और चेक करता है कि क्या बिंदु n परिभाषा को संतुष्ट करता है 2. इस मामले में, एन को जंप बिंदु और रिटर्न (रेखा 5, 7 और 11) द्वारा इंगित किया गया है। यदि n एक जंप पॉइंट नहीं है, तो एल्गोरिथ्म पुन: दोहराता है और d दिशा में फिर से आगे बढ़ता है, लेकिन इस बार n नया रिपोर्टिंग पॉइंट (लाइन 12) है। एक बाधा का सामना करने पर पुनरावृत्ति बंद हो जाती है और आगे कोई कार्रवाई नहीं की जा सकती (पंक्ति 3)। यह ध्यान देने योग्य है कि प्रत्येक विकर्ण कदम से पहले, एल्गोरिथ्म को सीधे दिशाओं (9-11 लाइनों) में जंप पॉइंट्स का पता लगाना चाहिए। यह चेक डेफिनिशन 2 की तीसरी स्थिति से मेल खाता है और एल्गोरिथम की अनुकूलता बनाए रखने के लिए महत्वपूर्ण है।

संदर्भ

मूल में एल्गोरिथम का विवरण: harablog.wordpress.com/2011/09/07/jump-point-search
Js पर कार्यान्वयन: qiao.github.com/PathFinding.js/visual (जंप पॉइंट सर्च चुनें और दीवारें सेट करें)
Js कोड ही: github.com/qiao/PathFinding.js/blob/master/src/finders/JumpPointFinder.js
बेंचमार्क: github.com/Yonaba/Jumper-Benchmark
विस्तृत विज़ुअलाइज़र: zerowidth.com/2013/05/05/jump-point-search-explained.html