K- साधन विधि (k- साधन) का उपयोग करके छवियों का सबसे सरल क्लस्टरिंग

अक्सर, जब किसी वीडियो में चलती वस्तुओं की खोज की जाती है, या तो पृष्ठभूमि, समय के अंतर, या ऑप्टिकल प्रवाह को घटाकर, हम बहुत सारे बिंदुओं के साथ समाप्त होते हैं, जो कि उपरोक्त एल्गोरिदम के बाद, पिछले फ्रेम के सापेक्ष उनकी स्थिति को बदलने और अग्रभूमि से संबंधित होने के रूप में चिह्नित हैं।



इस तरह के प्रसंस्करण के बाद, क्लस्टर विश्लेषण पद्धति का उपयोग करके वस्तुओं को खंडित करने पर सवाल उठता है, जिसे नीचे चर्चा की जाएगी और सी ++ में इसके वास्तविक कार्यान्वयन पर चर्चा की जाएगी।

वस्तु विभाजन

पहला, थोड़ा सिद्धांत:
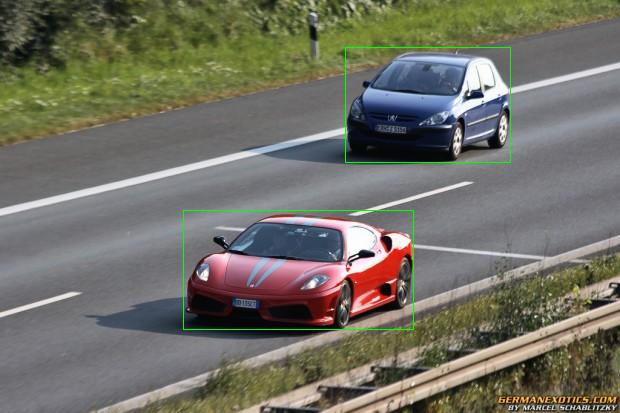
विभाजन एक डिजिटल छवि को कई खंडों (पिक्सेल के सेट) में विभाजित करने की प्रक्रिया है। सीधे शब्दों में कहें, यह एक ऐसी चीज है जो आपको यह निर्धारित करने की अनुमति देती है कि इस सेट से कौन से पिक्सेल फेरारी के हैं, और कौन से प्यूज़ो के हैं।
कम्प्यूटेशनल संसाधनों के दृष्टिकोण से, विभाजन के लिए क्लस्टर विश्लेषण विधियों का उपयोग बहुत प्रभावी है। क्लस्टरिंग का सार यह है कि सभी मूल ऑब्जेक्ट (इस मामले में, पिक्सेल) को कई असंतुष्ट समूहों में विभाजित किया जाता है ताकि एक ही समूह में आने वाली वस्तुओं में समान विशेषताएं हों, जबकि विभिन्न समूहों से वस्तुओं के लिए इन विशेषताओं में काफी होना चाहिए। अलग होना। परिणामी समूहों को क्लस्टर कहा जाता है। क्लस्टरिंग के लिए सबसे सरल विधि में प्रारंभिक मान पिक्सेल निर्देशांक (x, y) हैं, अधिक जटिल मामलों में, उदाहरण के लिए, ग्रेस्केल छवियों के लिए, एक त्रि-आयामी वेक्टर (x, y, I (x, y)) का उपयोग किया जाता है, जहां I (x, y) - भूरे रंग
और अगर आरजीबी का इस्तेमाल किया जाए तो पांच आयामी वेक्टर।

K- साधन विधि

सेंट्रोइड एक बिंदु है जो एक क्लस्टर का केंद्र है।
k- साधन (k- साधन) सबसे लोकप्रिय क्लस्टरिंग विधि है। एल्गोरिथ्म को व्यापक रूप से इसके कार्यान्वयन में आसानी के कारण पसंद किया जाता है, उच्च गति (और यह वीडियो के साथ काम करते समय बहुत महत्वपूर्ण है)।
एल्गोरिदम ऐसा है जो इन समूहों के केंद्रों से समूहों के बिंदुओं के कुल द्विघात विचलन को कम करने का प्रयास करता है। आम लोगों में, यह एक पुनरावृत्त एल्गोरिथ्म है जो पिक्सेल के दिए गए सेट को उन बिंदुओं के k समूहों में विभाजित करता है जो अपने केंद्रों के जितना संभव हो, और इन केंद्रों के विस्थापन के कारण क्लस्टरिंग स्वयं होती है। इस तरह के सिद्धांत को विभाजित और शासन करें।
यह भी ध्यान दिया जाना चाहिए कि k- साधन विधि शोर के प्रति बहुत संवेदनशील है, जो क्लस्टरिंग के परिणामों को महत्वपूर्ण रूप से विकृत कर सकती है। इसलिए, आदर्श रूप से, क्लस्टरिंग से पहले, आपको इसे कम करने के लिए डिज़ाइन किए गए फिल्टर के माध्यम से फ़्रेम चलाने की आवश्यकता है।

यहाँ k- साधन विधि द्वारा सरलतम क्लस्टरिंग का बहुत सिद्धांत दिया गया है:

1. यह k पिक्सेल के सेट से चयन करना आवश्यक है जो पिक्सेल के अनुरूप k समूहों के केन्द्रक होंगे।
   प्रारंभिक सेंट्रोइड्स का चयन या तो यादृच्छिक हो सकता है या एक निश्चित एल्गोरिदम के अनुसार हो सकता है।
   
2. हम एक चक्र में प्रवेश करते हैं जो तब तक जारी रहता है जब तक कि क्लस्टर के केंद्रक अपनी स्थिति बदलने के लिए संघर्ष नहीं करते।
3. हम प्रत्येक पिक्सेल के चारों ओर जाते हैं और देखते हैं कि यह किस सेंट के पास है।
4. पास के एक केन्द्रक पाया? इस सेंट्रोइड के क्लस्टर में एक पिक्सेल बांधें।
5. सभी पिक्सेल के माध्यम से क्रमबद्ध? अब आपको k समूहों के केन्द्रक के नए निर्देशांक की गणना करने की आवश्यकता है।
6. अब नए सेंट्रोइड्स के निर्देशांक की जांच करें। यदि वे क्रमशः पिछले सेंट्रोइड्स के बराबर हैं, तो हम चक्र से बाहर निकलते हैं, यदि नहीं, तो हम बिंदु 3 पर लौटते हैं।

यहाँ एक चित्र है जो लगभग एल्गोरिथ्म के संचालन को प्रदर्शित करता है:

यहाँ k- साधन एल्गोरिथ्म के संचालन का वर्णन करने के लिए एक अच्छा एप्लेट है

चलिए शुरू करते हैं

शुरू करने के लिए, हमें एक वर्ग की आवश्यकता है, आइए इसे क्लस्टर कहते हैं, जो क्लस्टर से संबंधित पिक्सेल के निर्देशांक के वेक्टर को संग्रहीत करेगा, जो सेंट्रोइड के निर्देशांक के वर्तमान और पिछले मान हैं:

class Cluster{ vector<POINT> scores; public: int curX , curY;//   int lastX, lastY;//   size_t Size(){ return scores.size();}//   inline void Add(POINT pt){ scores.push_back(pt); }//    void SetCenter(); void Clear();//  static Cluster* Bind(int k, Cluster * clusarr, vector<POINT>& vpt); static void InitialCenter(int k, Cluster * clusarr , vector<POINT>& vpt);; static void Start(int k, Cluster * clusarr, vector<POINT>& vpt); inline POINT& at(unsigned i){ return scores.at(i);}//    }; 

अब हमें ऐसी विधि को लागू करने की आवश्यकता है जो केन्द्रक के प्रारंभिक निर्देशांक को वितरित करेगी। बेशक, आप कुछ अधिक जटिल कर सकते हैं, लेकिन हमारे मामले में वेक्टर पर एक समान वितरण में कमी आएगी:

 void Cluster::InitialCenter(int k, Cluster * clusarr, vector<POINT>& vpt){ int size = vpt.size(); int step = size/k; int steper = 0; for(int i = 0;i < k;i++,steper+=step){ clusarr[i].curX = vpt[steper].x; clusarr[i].curY = vpt[steper].y; } } 

आपको एक ऐसी विधि भी लिखनी होगी, जो पैराग्राफ 5 के अनुसार सेंट्रोइड के नए निर्देशांक खोजने के लिए ज़िम्मेदार होगी। क्लस्टर के पिक्सल के चारों ओर आयत का वर्णन करके नए सेंट्रोइड के निर्देशांक पाए जा सकते हैं और फिर सेंट्रोइड इसके विकर्णों का प्रतिच्छेदन होगा।

 void Cluster::SetCenter(){ int sumX = 0, sumY = 0; int i = 0; int size = Size(); for(; i<size;sumX+=scores[i].x,i++);//the centers of mass by x i = 0; for(; i<size;sumY+=scores[i].y, i++);//the centers of mass by y lastX = curX; lastY = curY; curX = sumX/size; curY = sumY/size; } void Cluster::Clear(){ scores.clear(); } 

और अब यह खंडों के माप की तुलना करने के सिद्धांत द्वारा एक विशेष क्लस्टर के लिए "लिंकिंग" पिक्सल की एक सरल विधि बनाने के लिए बनी हुई है:

 Cluster * Cluster::Bind(int k, Cluster * clusarr, vector<POINT>& vpt){ for(int j = 0; j < k;j++) clusarr[j].Clear();//     int size = vpt.size(); for(int i = 0; i < size; i++){//       int min = sqrt( pow((float)clusarr[0].curX-vpt[i].x,2)+pow((float)clusarr[0].curY-vpt[i].y,2) ); Cluster * cl = &clusarr[0]; for(int j = 1; j < k; j++){ int tmp = sqrt( pow((float)clusarr[j].curX-vpt[i].x,2)+pow((float)clusarr[j].curY-vpt[i].y,2) ); if(min > tmp){ min = tmp; cl = &clusarr[j];}//    } cl->Add(vpt[i]);//        } return clusarr; } 

और अंत में मुख्य लूप:

 void Cluster::Start(int k, Cluster * clusarr, vector<POINT>& vpt){ Cluster::InitialCenter(k,clusarr,vpt); for(;;){//   int chk = 0; Cluster::Bind(k,clusarr,vpt);//    for(int j = 0; j < k;j++)//    clusarr[j].SetCenter(); for(int p = 0; p<k;p++)//       - if(clusarr[p].curX == clusarr[p].lastX && clusarr[p].curY == clusarr[p].lastY) chk++; if(chk == k) return;//     } } 

और इस सब से क्या?

आइए हम मशीनों के साथ तस्वीर पर लौटते हैं, चलती वस्तुओं को गुदगुदाते हैं। के-साधन एल्गोरिथ्म का उपयोग करते समय एक समस्या उत्पन्न होती है, अर्थात्, हम नहीं जानते कि इस दृश्य में कितनी चलती हुई वस्तुएं होंगी, हालांकि हम लगभग अनुमान लगा सकते हैं। उदाहरण के लिए, कारों के साथ एक फ्रेम, उस दृश्य पर यह मान लेना उचित होगा कि वहाँ अधिकतम 10 कारें होंगी। इस प्रकार, प्रोग्राम इनपुट k = 10 से पूछते हुए और 10 समूहों के बिंदुओं को हरे रंग के आयतों के साथ परिक्रमा करते हुए, हमें निम्नलिखित चित्र मिलते हैं:



अब, केवल प्रतिच्छेदन आयतों में शामिल होने से, हम परिणामी समूहों को ढूंढते हैं, उन्हें एक आयत के साथ चक्कर लगाते हुए हम पोस्ट की शुरुआत में परिवर्तित छवि प्राप्त करते हैं। यह सरल है।