बहुक्रिया और साझा सरणी का उपयोग करके पायथन में समानांतर प्रोग्रामिंग

परिचय।

अजगर एक अद्भुत भाषा है। मेरी राय में, पायथन + न्यूपी + मैटलोट्लिब गुच्छा, अब वैज्ञानिक गणना और एल्गोरिदम के तेजी से प्रोटोटाइप के लिए सबसे अच्छा में से एक है। लेकिन प्रत्येक उपकरण के अपने प्रकाश और अंधेरे पक्ष हैं। पायथन की सबसे चर्चित विशेषताओं में से एक जीआईएल है - ग्लोबल इंटरप्रेटर लॉक। मैं इस फीचर को इंस्ट्रूमेंट के डार्क साइड में देना चाहूंगा। हालांकि कई मुझसे सहमत नहीं हैं।

संक्षेप में, जीआईएल एक पायथन इंटरप्रेटर में कुशलता से एक से अधिक धागे का उपयोग करने की अनुमति नहीं देता है। जीआईएल के अधिवक्ताओं का तर्क है कि जीआईएल के साथ एकल-थ्रेडेड प्रोग्राम बहुत अधिक कुशलता से काम करते हैं। लेकिन जीआईएल की उपस्थिति का मतलब है कि कई थ्रेड और साझा मेमोरी का उपयोग करके समानांतर कंप्यूटिंग संभव नहीं है। और यह आधुनिक मल्टी-कोर दुनिया में काफी मजबूत सीमा है।

सी ++ थ्रेड्स के साथ जीआईएल को दूर करने का एक तरीका हाल ही में एक लेख में चर्चा की गई थी: एक मल्टीथ्रेडेड सी ++ एप्लिकेशन में पायथन का उपयोग करना । मैं बहुप्रचलित और साझा सरणी के आधार पर GIL की सीमाओं को दूर करने के लिए एक और तरीके पर विचार करना चाहता हूं। मेरी राय में, यह विधि कई थ्रेड्स और साझा की गई मेमोरी की पारदर्शी समानांतर प्रोग्रामिंग के लिए प्रक्रियाओं को और साझा की गई मेमोरी को काफी सरल और कुशलता से उपयोग करना संभव बनाती है।

टास्क।

एक उदाहरण के रूप में, निम्नलिखित समस्या पर विचार करें। तीन-आयामी अंतरिक्ष में, एन अंक v0, v1, ..., vN दिए गए हैं। उनके बीच की दूरी के आधार पर किसी फ़ंक्शन की गणना करने के लिए प्रत्येक जोड़ी बिंदुओं की आवश्यकता होती है। परिणाम इस फ़ंक्शन के मूल्यों के साथ एक NxN मैट्रिक्स होगा। एक फ़ंक्शन के रूप में, हम निम्नलिखित लेते हैं: f = r ^ 3/12 + r ^ 2 / 6. यह परीक्षण, वास्तव में, इतना सिंथेटिक नहीं है। आरबीएफ प्रक्षेप, जिसका उपयोग कम्प्यूटेशनल गणित के कई क्षेत्रों में किया जाता है, दूरी के कार्य के रूप में ऐसे कार्यों की गणना पर आधारित है।

समांतर विधि।

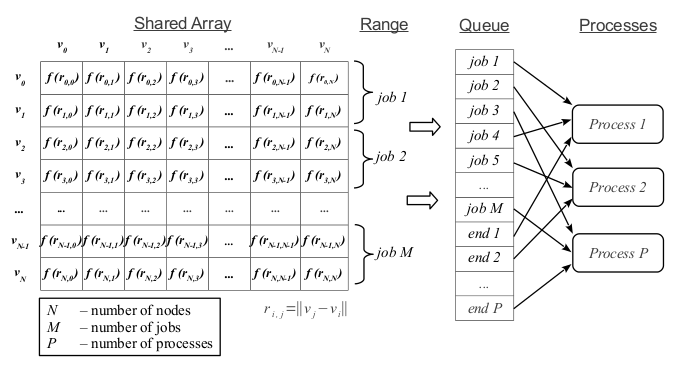
इस समस्या में, मैट्रिक्स की प्रत्येक पंक्ति की गणना स्वतंत्र रूप से की जा सकती है। मैट्रिक्स की प्रत्येक कुछ पंक्तियों से, हम स्वतंत्र नौकरियां बनाते हैं और उन्हें नौकरी की कतार में रखते हैं (चित्र 1 देखें)। चलो कुछ प्रक्रियाएँ शुरू करते हैं। प्रत्येक प्रक्रिया कतार से निष्पादन के लिए अगला कार्य करेगी जब तक कि यह कोड "अंत" के साथ एक विशेष कार्य का सामना न करे। इस मामले में, प्रक्रिया अपना काम समाप्त कर देती है।

पायथन कार्यान्वयन।

पायथन कार्यान्वयन में, हमारे दो मुख्य तरीके होंगे: mpCalcDistance (नोड्स) और
mpCalcDistance_Worker (नोड्स, कतार, arrD)। MpCalcDistance (नोड) विधि नोड्स की एक सूची को स्वीकार करता है, एक साझा मेमोरी क्षेत्र बनाता है, एक नौकरी कतार तैयार करता है, और प्रक्रियाएं शुरू करता है। MpCalcDistance_Worker विधि (नोड्स, कतार, arrD) एक कम्प्यूटेशनल विधि है जो अपने स्वयं के धागे में चलती है। यह इनपुट के रूप में नोड्स, एक नौकरी कतार और एक साझा मेमोरी क्षेत्र की सूची लेता है। इन विधियों के कार्यान्वयन पर अधिक विस्तार से विचार करें।

MpCalcDistance (नोड्स) विधि

एक साझा मेमोरी क्षेत्र बनाएँ:

nP = nodes.shape[0] nQ = nodes.shape[0] arrD = mp.RawArray(ctypes.c_double, nP * nQ) 

एक नौकरी कतार बनाएँ। प्रत्येक कार्य एक मैट्रिक्स की लाइनों की एक सीमा के अलावा कुछ भी नहीं है। विशेष मूल्य कोई भी प्रक्रिया समाप्त करने का संकेत नहीं है:

  nCPU = 2 nJobs = nCPU * 36 q = nP / nJobs r = nP % nJobs jobs = [] firstRow = 0 for i in range(nJobs): rowsInJob = q if (r > 0): rowsInJob += 1 r -= 1 jobs.append((firstRow, rowsInJob)) firstRow += rowsInJob queue = mp.JoinableQueue() for job in jobs: queue.put(job) for i in range(nCPU): queue.put(None) 

हम प्रक्रिया बनाते हैं और तब तक इंतजार करते हैं जब तक कि नौकरी की कतार समाप्त नहीं हो जाती:

  workers = [] for i in range(nCPU): worker = mp.Process(target = mpCalcDistance_Worker, args = (nodes, queue, arrD)) workers.append(worker) worker.start() queue.join() 

साझा मेमोरी के क्षेत्र से, हम परिणामों के साथ एक मैट्रिक्स बनाते हैं:

  D = np.reshape(np.frombuffer(arrD), (nP, nQ)) return D 

MpCalcDistance_Worker विधि (नोड्स, कतार, arrD)

हम साझा मेमोरी क्षेत्र को एक मैट्रिक्स में लपेटते हैं:

  nP = nodes.shape[0] nQ = nodes.shape[0] D = np.reshape(np.frombuffer(arrD), (nP, nQ)) 

जब तक नौकरी की कतार खत्म नहीं हो जाती, तब तक कतार से अगली नौकरी लें और गणना करें:

  while True: job = queue.get() if job == None: break start = job[0] stop = job[0] + job[1] # components of the distance vector p = nodes[start:stop] q = nodes.T Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D[start:stop, :] = L * L * L / 12 + L * L / 6 queue.task_done() 

परिणाम

रनटाइम वातावरण: दोहरे कोर प्रोसेसर, उबंटू 12.04, 64 बिट।


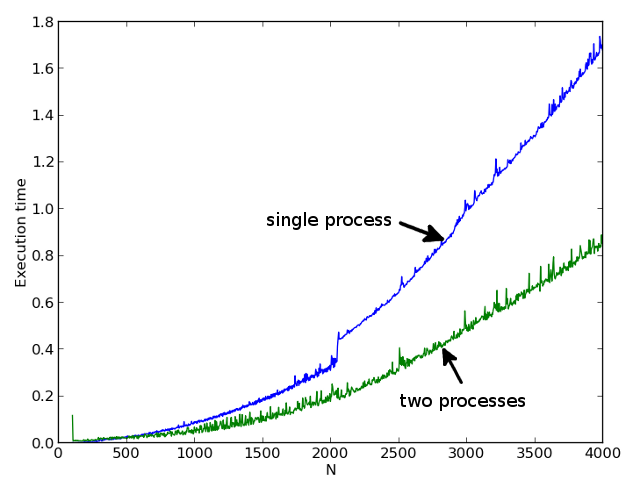
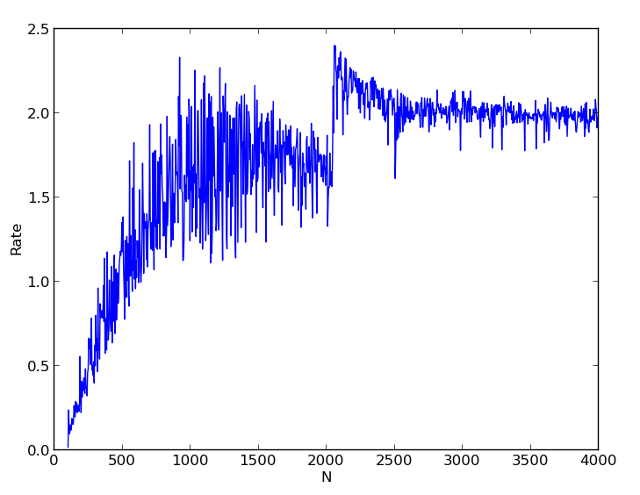
पहली तस्वीर अलग-अलग एन के लिए एकल-थ्रेडेड और दो-थ्रेडेड गणना का समय दिखाती है। दूसरी तस्वीर एकल-थ्रेडेड गणना के समय के अनुपात को दो-थ्रेडेड से दर्शाती है। यह देखा जा सकता है कि एन = 500 से शुरू होकर हमें पहले से ही गणना का एक महत्वपूर्ण त्वरण प्राप्त होता है।

एन = 2000 के क्षेत्र में एक बहुत ही दिलचस्प परिणाम प्राप्त होता है। एकल-थ्रेडेड संस्करण में, हमें गणना समय में ध्यान देने योग्य कूद मिलता है, और बहु-थ्रेडेड गणना में, त्वरण गुणांक 2 से अधिक हो जाता है। मैं कैश प्रभाव द्वारा समझाता हूं। एक बहु-थ्रेडेड संस्करण में, प्रत्येक कार्य के लिए डेटा पूरी तरह से कैश है। लेकिन सिंगल-थ्रेडेड में नहीं है।

तो प्रक्रियाओं और साझा स्मृति का उपयोग, मेरी राय में, बस आपको जीआईएल की सीमाओं को दरकिनार करने की अनुमति देता है।

पूरी स्क्रिप्ट का पूरा कोड:

 """ Python multiprocessing with shared memory example. This example demonstrate workaround for the GIL problem. Workaround uses processes instead of threads and RawArray allocated from shared memory. See also: [1] http://docs.python.org/2/library/multiprocessing.html [2] http://folk.uio.no/sturlamo/python/multiprocessing-tutorial.pdf [3] http://www.bryceboe.com/2011/01/28/the-python-multiprocessing-queue-and-large-objects/ """ import time import ctypes import multiprocessing as mp import numpy as np import matplotlib.pyplot as plt def generateNodes(N): """ Generate random 3D nodes """ return np.random.rand(N, 3) def spCalcDistance(nodes): """ Single process calculation of the distance function. """ p = nodes q = nodes.T # components of the distance vector Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D = L * L * L / 12 + L * L / 6 return D def mpCalcDistance_Worker(nodes, queue, arrD): """ Worker process for the multiprocessing calculations """ nP = nodes.shape[0] nQ = nodes.shape[0] D = np.reshape(np.frombuffer(arrD), (nP, nQ)) while True: job = queue.get() if job == None: break start = job[0] stop = job[0] + job[1] # components of the distance vector p = nodes[start:stop] q = nodes.T Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D[start:stop, :] = L * L * L / 12 + L * L / 6 queue.task_done() queue.task_done() def mpCalcDistance(nodes): """ Multiple processes calculation of the distance function. """ # allocate shared array nP = nodes.shape[0] nQ = nodes.shape[0] arrD = mp.RawArray(ctypes.c_double, nP * nQ) # setup jobs #nCPU = mp.cpu_count() nCPU = 2 nJobs = nCPU * 36 q = nP / nJobs r = nP % nJobs jobs = [] firstRow = 0 for i in range(nJobs): rowsInJob = q if (r > 0): rowsInJob += 1 r -= 1 jobs.append((firstRow, rowsInJob)) firstRow += rowsInJob queue = mp.JoinableQueue() for job in jobs: queue.put(job) for i in range(nCPU): queue.put(None) # run workers workers = [] for i in range(nCPU): worker = mp.Process(target = mpCalcDistance_Worker, args = (nodes, queue, arrD)) workers.append(worker) worker.start() queue.join() # make array from shared memory D = np.reshape(np.frombuffer(arrD), (nP, nQ)) return D def compareTimes(): """ Compare execution time single processing versus multiple processing. """ nodes = generateNodes(3000) t0 = time.time() spD = spCalcDistance(nodes) t1 = time.time() print "single process time: {:.3f} s.".format(t1 - t0) t0 = time.time() mpD = mpCalcDistance(nodes) t1 = time.time() print "multiple processes time: {:.3f} s.".format(t1 - t0) err = np.linalg.norm(mpD - spD) print "calculate error: {:.2e}".format(err) def showTimePlot(): """ Generate execution time plot single processing versus multiple processing. """ N = range(100, 4000, 4) spTimes = [] mpTimes = [] rates = [] for i in N: print i nodes = generateNodes(i) t0 = time.time() spD = spCalcDistance(nodes) t1 = time.time() sp_tt = t1 - t0 spTimes.append(sp_tt) t0 = time.time() mpD = mpCalcDistance(nodes) t1 = time.time() mp_tt = t1 - t0 mpTimes.append(mp_tt) rates.append(sp_tt / mp_tt) plt.figure() plt.plot(N, spTimes) plt.plot(N, mpTimes) plt.xlabel("N") plt.ylabel("Execution time") plt.figure() plt.plot(N, rates) plt.xlabel("N") plt.ylabel("Rate") plt.show() def main(): compareTimes() #showTimePlot() if __name__ == '__main__': main()