लोबाचेव्स्की विमान पर जीवन

गेम "लाइफ" के विभिन्न कार्यान्वयनों का वर्णन हैबे पर पहले से ही बार-बार किया गया है। इस लेख में, इस विषय की निरंतरता के रूप में, एक और विकल्प पर विचार किया जाता है: लॉबिक विमान पर एक नियमित ग्रिड का उपयोग खेल मैदान के रूप में किया जाता है। कार्यक्रमों में लोबाचेव्स्की विमान का उपयोग करने के सामान्य तरीके और इसके लिए आवश्यक गणितीय तरीके वर्णित हैं।
लोबाचेव्स्की विमान कैसे उत्पन्न हुआ यह सर्वविदित है। आखिरी से पहले की शताब्दी में, मेसर्स। गॉस, लोबचेवस्की और बोवाई, जो उस समय यूरोप के अलग-अलग देशों में एक ही समय में रहते थे, ने सोचा कि अगर यूक्लिड के पांचवें पोस्ट को रद्द कर दिया गया और विपरीत स्वयंसिद्ध के साथ बदल दिया गया तो क्या होगा। यह पता चला कि कुछ भी बुरा नहीं होगा, और कोई विरोधाभास पैदा नहीं होगा। गैर-यूक्लिडियन ज्यामिति के बाद के अध्ययन का एक महत्वपूर्ण हिस्सा यह पता लगाने के लिए समर्पित था कि उनमें से कौन इस ज्यामिति के विचार को चुरा लेता है।
यह ज्ञात नहीं है कि गैर-यूक्लिडियन ज्यामिति का निर्धारण करने के "नकारात्मक" तरीके के बावजूद (कहने के बजाय कि बिल्कुल एक सीधी रेखा एक बिंदु से गुजरती है और किसी दिए गए को नहीं काटती है, हम कहते हैं कि ऐसी कई लाइनें हो सकती हैं), हालांकि, हम प्रमेयों और सूत्रों की एक प्रणाली प्राप्त करते हैं जो यूक्लिडियन ज्यामिति की तुलना में कम सामंजस्यपूर्ण नहीं है। और एक ही समय में, हमारे पास ज्यामितीय आकृतियों की अधिक विविधता है, जिसमें विमान के विभाजन को नियमित बहुभुजों में शामिल किया गया है।



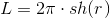
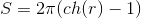
तो, प्रमेय। पाइथागोरस प्रमेय, जो ² + बी ² = सी ^{2 की} तरह लग रहा था, लोबाचस्की ज्यामिति में फॉर्म ch (a) ch (b) = ch (c) लेता है, परिधि है और सर्कल का क्षेत्र है । यहाँ श (x) हाइपरबोलिक साइन है, और ch (x) हाइपरबोलिक कोसाइन है। ऐसी स्वतंत्रता के साथ दूरी के लिए गणितीय कार्यों को लागू करने में सक्षम होने के लिए, हमें माप की एक निश्चित पूर्ण इकाई की आवश्यकता होती है, जो लोबाचेव्स्की की ज्यामिति में मौजूद है (यह वह दूरी है जिस पर "परिवर्तित" लाइनों के बीच की दूरी ठीक समय से कम हो जाएगी)। दूरी की इस तरह की एक इकाई की उपस्थिति तुरंत इस तथ्य की ओर ले जाती है कि समानता परिवर्तन गायब हो जाता है - यदि हम दूरी को किसी संख्या में उसी समय में बदलने की कोशिश करते हैं, तो आकृति का आकार बदल जाएगा। उदाहरण के लिए, एक नियमित त्रिभुज का कोण इसकी तरफ निर्भर करता है।
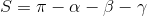
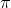
लेकिन तीन कोणों पर एक त्रिकोण का निर्माण संभव हो जाता है (यह दूसरी कोसाइन प्रमेय का उपयोग करके किया जाता है)। और त्रिभुज का क्षेत्रफल ज्ञात करना काफी सरल है: । यह देखा जा सकता है कि त्रिभुज के कोणों का योग हमेशा कम होता है , और इसे मनमाने ढंग से छोटा किया जा सकता है (त्रिभुज के किनारे अनंत की ओर बढ़ेंगे, लेकिन क्षेत्र परिमित रहेगा)।
एक कोण के साथ सही त्रिकोण चुनना , हमें नियमित त्रिभुजों से "लकड़ी की छत" बनाने का अवसर मिलता है, जिसमें 7.8 एक शीर्ष पर परिवर्तित होता है ... त्रिकोण के अनंत तक ("अल्ट्रा-इन्फिनिटी" का विकल्प भी है, लेकिन हम इसके बारे में बात नहीं करेंगे)। इस लेख में हम पैराकेट में रुचि लेंगे {4,5} , जिसमें 72 ^{ओ के} कोण के साथ नियमित चतुष्कोण शामिल हैं। दुर्भाग्य से, हम अभी तक इसे बनाने के लिए तैयार नहीं हैं।
हमारी सामान्य सीधी रेखा और सर्कल के अलावा, लोबाचेव्स्की विमान पर समान गुणों वाली दो और लाइनें हैं - एक समबाहु या एक हाइपरसाइकल (उस से एक ही तरफ की रेखा से दूरी पर स्थित बिंदुओं का सेट) और सीमा रेखा "या कुंडली (लाइन इंटरसेक्टिंग) समकोण पर सीधी रेखाओं को परिवर्तित करने का एक गुच्छा, अनंत तक झुकाव वाली त्रिज्या वाली एक वृत्त की सीमा।) तीन प्रकार के विमान चालन हैं - सामान्य घुमाव (एक बिंदु और एक कोण द्वारा परिभाषित), एक सीधी रेखा (एक सीधी रेखा और एक ऑफसेट द्वारा परिभाषित) के साथ एक बदलाव और पूर्व के साथ एक बदलाव। सीधी रेखा एक बहुत ही अजीब गति है, जिसके बारे में यह नहीं कहा जा सकता है कि "हम कितना आगे बढ़ गए हैं" (विमान के विभिन्न स्थानों में, शिफ्ट की भयावहता अलग है, और ऐसे सभी बदलाव किसी भी मायने में समान हैं।) यह महत्वपूर्ण है कि सीधी रेखा के साथ बदलाव बिल्कुल नहीं है। यूक्लिडियन विमान पर समानान्तर स्थानांतरण जैसी ही बात: अलग-अलग बिंदुओं को अलग-अलग दूरियों द्वारा स्थानांतरित किया जाता है (कतरनी अक्ष पर स्थित बिंदु सबसे कम होते हैं), स्थानांतरण करते समय रेखा अपनी छवि के साथ अंतर कर सकती है। सामान्य तौर पर, लोबाचेव्स्की विमान पर "वेक्टर" की कोई अवधारणा नहीं है, लेकिन "दिशा" की अवधारणा के साथ बहुत मुश्किलें हैं।
इस विमान के साथ काम करने के लिए, हमें एक समन्वय प्रणाली की आवश्यकता है। इसे दर्ज करना और यहां तक ​​कि यह काम करने के लिए सुविधाजनक था, आसान नहीं है। कार्टेशियन निर्देशांक का कोई एनालॉग नहीं है (बराबर x और y के साथ )। आप एक सीधी रेखा पर प्रक्षेपण और उससे दूरी पर बिंदु का उपयोग कर सेट कर सकते हैं, लेकिन यह बहुत सुविधाजनक नहीं होगा। ध्रुवीय निर्देशांक में काम करना बेहतर है, या कुछ सीमा रेखा को अक्ष के रूप में लेना (एक समन्वय इस रेखा पर एक बिंदु का प्रक्षेपण है, दूसरा इसके लिए दूरी है)। सौभाग्य से, ये समन्वय प्रणालियां पॉइनकेयर द्वारा आविष्कार किए गए बहुत सुविधाजनक मॉडल बनाने के लिए संभव बनाती हैं।

डिस्क और ऊपरी आधा विमान। सावधानी, TFKP!

यदि हम सीमा रेखा को लेते हैं, तो उस बिंदु के प्रक्षेपण को x द्वारा निरूपित करें, और y से बिंदु से रेखा तक दूरी के घातांक पर ध्यान दें (संकेत को ध्यान में रखते हुए, दूरी को माना जाता है
इस लाइन के "अवतल" पक्ष से सकारात्मक), और यूक्लिडियन विमान पर निर्देशांक (x, y) के साथ बिंदुओं पर विचार करें, हमें एक आश्चर्यजनक तथ्य मिलता है। पूरा लोबाचेव्स्की विमान ऊपरी आधे तल ( y> 0 ) में बदल जाएगा, लाइनें या तो ऊर्ध्वाधर रेखाओं में या हलकों के चापों में बदल जाएंगी (केंद्र y = 0 पर केंद्रों के साथ), मंडलियां हलकों के साथ रहेंगी (शिफ्ट किए गए केंद्र के साथ, और सभी समवर्ती और सीमा रेखाएं भी हलकों के सीधे या चाप बन जाते हैं। इसके अलावा, लाइनों और हलकों के बीच सभी कोण बने रहेंगे।
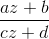
इस तरह के मॉडल को पोनकेरे "आधा विमान" मॉडल कहा जाता है। इस मॉडल में लॉबाचेव्स्की विमान के विस्थापन रूपांतरणों की तरह दिखेंगे जो सीधी रेखा y = 0 को संरक्षित करते हैं, और सीधी रेखाओं और हलकों को सीधी रेखाओं या हलकों (मोबियस ट्रांसफ़ॉर्मेशन) में अनुवाद करते हैं। यदि अंकों (x, y) के बजाय हम जटिल संख्या z = x + iy लेते हैं, तो ऐसे परिवर्तन रेखीय आंशिक कार्यों की तरह दिखाई देंगे , और संख्या a, b, c, d वास्तविक होना चाहिए। इन परिवर्तनों के बारे में क्या अच्छा है कि उनकी संरचना मैट्रिक्स गुणन की तरह व्यवहार करती है । यह हमें लोबाचेव्स्की विमान के कार्यान्वयन के लिए पहला सुराग देता है: लोबाचेवस्की विमान के विस्थापन को वास्तविक गुणांक के साथ 2x2 मेट्रिसेस के रूप में दर्शाया जा सकता है, एक संख्या से गुणा करने के लिए निर्धारित (यानी, मैट्रिसेस) और वही माना जाता है)।
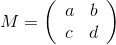
आगे, एम (जेड) के माध्यम से, जहां एक 2x2 मैट्रिक्स है, और z एक जटिल संख्या है, हम मात्रा को निरूपित करेंगे ।
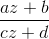
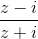
मेट्रिसेस और ऊपरी आधे विमान के साथ काम करना सुविधाजनक है, लेकिन बहुत स्पष्ट नहीं है। लोबाचस्की विमान की कल्पना करने के लिए, परिवर्तन को आमतौर पर इस आधे विमान पर लागू किया जाता है , और त्रिज्या का एक घेरा प्राप्त करें। 1. सीधे लोबाचेव्स्की विमान इस वृत्त के व्यास के रूप में निकलते हैं और अपनी सीमा के लंबवत होते हैं। इस मॉडल को पॉइनकेयर डिस्क कहा जाता है, हम इसका उपयोग परिणामों को आउटपुट करने के लिए करेंगे।

विभाजन {४,५}। सावधानी रैखिक बीजगणित!

खेल "जीवन" को लागू करने के लिए, एक लकड़ी की छत {4,5} को चुना गया था (विमान का नियमित 4-गोंन्स में विभाजन, प्रत्येक शीर्ष पर 5 कोशिकाएं अभिसरण होती हैं)। यह दो भागों में से एक है जो हमारे मानक विभाजन {4.4} के समान है। आउटपुट के दौरान क्वाड्रैंगल्स की विकृतियां बहुत बड़ी नहीं होंगी, और यह हमें एक ही समय में विमान का एक बड़ा टुकड़ा देखने की अनुमति देगा। उल्लिखित विभाजनों में से दूसरा {5,4} (प्रत्येक शीर्ष पर 4 पेंटागन अभिसरण हैं), लेकिन प्रयोगों से पता चला है कि यह लकड़ी की छत जीवन के लिए थोड़ा कम उपयुक्त है।
विभाजन को बनाने और उपयोग करने के लिए {4,5}, हमें कुछ चीजें करना सीखना होगा। सबसे पहले, हमारे मॉडल में केंद्रों के केंद्र और कोने के निर्देशांक ढूंढें। दूसरे, किसी न किसी तरह से एक को अलग करने के लिए, जो पड़ोसी हैं, यह पता लगाने के लिए किसी तरह चतुष्कोणों की संख्या। और आपको यह भी सीखना होगा कि तस्वीर के केंद्र को कैसे बदलना है ताकि आप विमान के सुदूर हिस्सों का अध्ययन कर सकें, क्योंकि सभी सबसे दिलचस्प होते हैं, आमतौर पर जहां हम नहीं होते हैं।
सूचकांकों के जोड़े के साथ कोशिकाओं को लेबल करने की हमारी सामान्य विधि यहां काम नहीं करती है। आम तौर पर। लेकिन हम जानते हैं कि प्रत्येक सेल को केंद्रीय सेल से विमान को स्थानांतरित करके प्राप्त किया जाता है, यह आंदोलन एक 2x2 मैट्रिक्स द्वारा वर्णित है, और सेल का केंद्र केंद्रीय सेल के केंद्र की छवि होगा, अर्थात। इस विस्थापन पर बिंदु (0,1) = i इसके अलावा, हमारे पास की कोशिकाएं इस आंदोलन के साथ केंद्रीय एक से जुड़ी कोशिकाओं की छवियां हैं। तो लकड़ी की छत बनाने के लिए हमें निम्नलिखित की आवश्यकता है:

• विस्थापन के मैट्रिक्स का पता लगाएं जो केंद्रीय सेल का पड़ोसी लोगों में अनुवाद करता है;
• इन आंदोलनों की जंजीरों का निर्माण उन आंदोलनों को खोजने के लिए करें जो शेष कोशिकाओं को बनाते हैं;
• पहले से ही ज्ञात केंद्र के साथ एक सेल के निर्माण के लिए अग्रणी परिवर्तनों को बाहर करने के लिए;
• यह मत भूलो कि सर्कल का क्षेत्र बहुत जल्दी बढ़ता है, इसलिए हमें खोज की गहराई को अच्छी तरह से सीमित करना होगा;
• केंद्रीय सेल के कम से कम एक शीर्ष के समन्वय का पता लगाएं। इससे बची हुई चोटियों को बनाना आसान है।

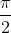
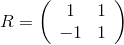
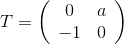
शुरू करने के लिए, हम कुछ आंदोलनों को चुनते हैं जिनसे हम अपनी जरूरत की हर चीज प्राप्त कर सकते हैं। इस तरह के एक आंदोलन को एक कोण से बिंदु I के आसपास R का रोटेशन होगा (वह केंद्रीय कोशिका का स्वयं में अनुवाद करता है), और दूसरा - टी समरूपता केंद्रीय सेल के एक पक्ष के मध्य के सापेक्ष - यह इस सेल को पड़ोसी को स्थानांतरित कर देगा। यह सत्यापित किया जा सकता है कि इन विस्थापन के मैट्रीस हैं और , जहां मैं * एक पड़ोसी सेल का केंद्र है (हम मानते हैं कि यह सीधे हमारे ऊपर स्थित है, इसलिए ए> 1 )। ए खोजने के लिए, समीकरण को हल करना आवश्यक होगा 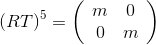कुछ मीटर के लिए ( आरटी सेल के कोने में से एक के चारों ओर एक रोटेशन है, और पहचान परिवर्तन है)। हम 5 वीं डिग्री के समीकरणों की प्रणाली को हल नहीं करना चाहते हैं, और यहां तक ​​कि विश्लेषणात्मक रूप से (हमें भविष्य में इसकी आवश्यकता होगी), इसलिए हम इसे अलग तरीके से करेंगे: कहते हैं कि मैट्रिक्स आरटी के आइजनवेल्यूज़ मैट्रिक्स के समान होने चाहिए , यानी। उनके विशिष्ट बहुपद संयोग होने चाहिए। गणनाओं को स्वीकार करते हुए, हम प्राप्त करते हैं कहाँ से

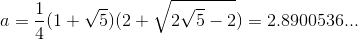
हम समीकरण RT (z) = z को हल करके चतुर्भुज के शीर्ष को ज्ञात करेंगे। यहां हमें संख्यात्मक समाधान की आवश्यकता नहीं है, बल्कि संख्यात्मक की आवश्यकता है।
जब हमने मेट्रिस आर और टी का निर्माण किया है, और यह सुनिश्चित किया है कि आर ⁴ और (आरटी) ⁵ स्केलर हैं, तो चतुर्भुज के एक जाली का निर्माण करना तकनीक का विषय है। हम सभी मेट्रिसेस M = R ^को TR ^b TR ^c T ... लेते हैं, जहाँ a, b, c, ... 1 से 3 तक की संख्याएँ हैं (संभवतः a = 0 ), और हम उन M की पहचान करते हैं जिनके लिए मैं (i) ) समान हैं। इस तरह के मेट्रिसेस का प्रत्येक वर्ग जाली का एक चतुर्भुज देता है। मैट्रिसेस M ₁ और M _{2 के} समान चतुर्भुज समीपस्थ होंगे यदि M ₂ = M ₁ R ^k TR TR कुछ k, l के लिए ।
प्लेन के सीमित क्षेत्र में खेलने के लिए यह पर्याप्त होगा। हमें केवल यह याद रखने की आवश्यकता है कि पड़ोसी कोशिकाओं के झुकाव को शुरू में समन्वित नहीं किया जाता है, इसलिए, यदि वे महत्वपूर्ण हैं, तो पड़ोसी सेल में जाने पर, आपको यह इंगित करना होगा कि हम किस पक्ष (उस सेल के उन्मुखीकरण में) से आए हैं। यह आसान नहीं है, लेकिन आपको इस टुकड़े को एक बार लिखना होगा :)।
विमान के निर्मित टुकड़े की कल्पना करने के लिए, हमें "कैमरा स्थिति" के मैट्रिक्स की भी आवश्यकता होगी। हमारे मामले में, यह सिर्फ एक 2x2 मैट्रिक्स है, जो कि कोशिकाओं की पहचान करने के लिए उपयोग किया जाता है। यदि कैमरे का मैट्रिक्स F है , तो हम मैट्रिक्स M द्वारा परिभाषित सेल को खींचना चाहते हैं, और इस सेल के समन्वय प्रणाली में बिंदु का समन्वय s ("आधा-प्लेन" मॉडल से एक जटिल संख्या) है, तो यह पता लगाने के लिए कि बिंदु की छवि Poincare की डिस्क पर कहाँ स्थित है, हम z पाते हैं। = F * M (s), w = (zi) / (z + i) । w वांछित बिंदु है।

Lobachevsky विमान पर बंद क्षेत्र। सावधानी, अंतिम क्षेत्र!

जैसा कि मैंने कहा, लोबाचेव्स्की विमान पर सर्कल का क्षेत्र बहुत तेज़ी से बढ़ रहा है। 1 से त्रिज्या बढ़ने से क्षेत्र में तीन का कारक बढ़ जाएगा। इसलिए, अगर हम पूछते हैं, उदाहरण के लिए, एक लाख कोशिकाएं, तो सबसे अच्छा वे एक सर्कल को 13 के त्रिज्या के साथ कवर करेंगे। खेल "लाइफ" के लिए यह पर्याप्त नहीं है, वे सीमाओं के बिना सजातीय क्षेत्रों को पसंद करते हैं। तो हमारे सामने चुनौती यह है कि हमारे लकड़ी की छत से एक टुकड़ा कैसे काटें और इसके किनारों को गोंद करें ताकि 5 चतुर्भुज अभी भी प्रत्येक शीर्ष पर स्थित हों? कार्टेसियन ग्रिड के लिए उपयोग की जाने वाली सरल विधि काम नहीं करती है - हमारे पास कोई आयत नहीं है। लेकिन वह एक संकेत देता है: वहाँ, अगर हम जाली से काटते हैं {4,4} एक वर्ग जिसके साथ P , जहाँ P अभाज्य है, तो हम कोशिकाओं (x ₁ , y ₁ ) और (x ₂ , y ₂ ) को समान मानते हैं, यदि x ₁ = x ₂ (mod P) और y ₁ = y ₂ (mod P) । हम ऐसा क्यों नहीं करते? 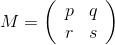प्रत्येक सेल में एक मैट्रिक्स होता है , जो कुछ मात्रा और क्रम में लिए गए मेट्रिस आर और टी का उत्पाद है। M ₂ = M ₁ R ^{k के} दो सेल एक कोशिका से मेल खाते हैं। हमें बस एक ऐसा पी चुनना है, जिसमें मैट्रिसेस आर और टी मोडुलो पी मौजूद हों।
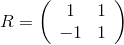
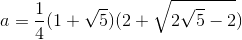
मैट्रिक्स के साथ सब कुछ सरल है - यह हमेशा मौजूद है। टी के लिए मौजूद है, अभिव्यक्ति परिकलित P की गणना (इसलिए हमें इसे विश्लेषणात्मक रूप में खोजने की आवश्यकता है)। मॉड्यूल पी की संख्या जिसके लिए ऐसी अभिव्यक्ति की गणना की जा सकती है वह छोटी है (लगभग हर 30 वें)। उदाहरण के लिए, पी = 179 । इस मॉड्यूल के अनुसार, हमें 1,433,790 सेल मिलते हैं, जो गेम के लिए काफी सामान्य है। वैसे भी, एक समय में हम उनमें से कुछ हजार ही देखते हैं।
मॉड्यूल को चुनने के बाद, हम आर और टी मोडुलो पी (एक स्थिर कारक तक) के सभी संभावित उत्पादों का निर्माण करते हैं - पी ³ पी से अधिक नहीं होगा। प्रत्येक मैट्रिक्स के लिए, उस सेल को याद रखें, जिससे यह मैट्रिक्स मेल खाती है (मैट्रिक्स एम और एमआर हमेशा एक ही सेल के अनुरूप होते हैं), और प्रत्येक सेल के लिए, कुछ मैट्रिक्स। फिर प्रत्येक कोशिका के लिए हम इसके सभी पड़ोसियों की संख्याओं को देखते हैं - अलग-अलग पक्षों पर, अलग-अलग - कोनों पर। और अंत में, जब सेल को परिभाषित करने वाले मैट्रिक्स एम के साथ मिलकर ज्यामितीय मॉडल का निर्माण करते हैं, तो हम एक ही डिग्री में आर (मॉड पी) और टी (मॉड पी) के उत्पाद की सावधानीपूर्वक गणना करते हुए, इसके प्रतिनिधित्व मॉडुलो पी पर विचार करेंगे।
हमने सब कुछ तय किया, आप काम करना शुरू कर सकते हैं। हम केवल ध्यान दें कि हमें ज्यामितीय मॉडल में बहुत अधिक कोशिकाओं की आवश्यकता नहीं है - हजारों हजारों पर्याप्त हैं। और ताकि इस मॉडल के माध्यम से आप खेल के मैदान के किसी भी हिस्से को देख सकें, हम ऐसा करेंगे।
मैट्रिक्स F (कैमरा पोजिशन) के अलावा, हम modulo P को देखते हुए मैट्रिक्स Q को भी स्टोर करेंगे - यह "कैमरे के नीचे फ़ील्ड का स्थान" होगा। विशेष रूप से, क्यू मैट्रिक्स स्वयं उस सेल के प्रतिनिधित्व में से एक होगा, जिसके ऊपर कैमरा स्थित है। ज्यामितीय मॉडल से नंबर k के साथ एक सेल बनाने के लिए, हम इस सेल से मैट्रिक्स M _k (mod P) लेते हैं, C _k = Q * (M _k (mod P)) की गणना करते हैं, और मैट्रिक्स C _k (इसी) के अनुरूप हमारे क्षेत्र से सेल का पता _{लगाते हैं।} हमने एक बार उसे याद किया)। और एफएम _के मैट्रिक्स का उपयोग करके सेल की पूरी सामग्री को आकर्षित करें, जैसा कि पिछले अनुभाग में वर्णित है।
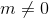
अगर कैमरे की आवाजाही के दौरान हम केंद्रीय सेल की सीमाओं से परे चले गए, और अब केंद्र में एक संख्या के लिए एक ज्यामितीय मॉडल का सेल तैयार किया गया है , फिर मॉडल पर क्षेत्र के प्रक्षेपण को स्थानांतरित करना होगा। मान लें कि अब हम कैमरे की स्थिति के रूप में F '= FM _{m का उपयोग} करेंगे, और क्षेत्र के स्थान के लिए Q' = Q (M _m (mod P)) को मैट्रिक्स के रूप में लेंगे। यदि यह काम नहीं करता है (लेकिन यह काम करना चाहिए), तो हम तुरंत देखेंगे - जब किसी क्षेत्र पर जा रहे हैं, तो छवि हमेशा लगातार नहीं चलेगी।

वास्तव में खेल "जीवन"

सामान्य तौर पर, कुछ भी दिलचस्प नहीं बचा था। लॉबचेवस्की विमान में मुख्य कार्य नेविगेशन था, और खेल "लाइफ" केवल सबसे सरल व्यावहारिक अनुप्रयोग था। लेकिन जब से हम यहाँ हैं ...
हमारे पास खेतों की एक सूची है। राज्य को स्थापित करना (सेल जीवित या मृत है) कोई समस्या नहीं है। समस्या दिलचस्प नियमों को चुनना है। बेशक, कॉनवे अपने 4-क्रम के नियमों के साथ, पकड़ने के लिए अवास्तविक है, लेकिन कम से कम मैं ग्लाइडर्स को पकड़ना चाहता हूं।
अधिक स्वतंत्रता रखने के लिए, पक्षों पर और कोनों में पड़ोसियों पर अलग-अलग विचार करने का निर्णय लिया गया था, और उनमें से प्रत्येक संयोजन के लिए अपना उत्तर "जीवित या मृत" दिया गया था। बहुत जल्द यह स्पष्ट हो गया कि यदि कोशिकाएं कम से कम 4 पड़ोसियों की उपस्थिति में जीवन में आती हैं, तो हम ग्लाइडर्स नहीं देखेंगे, और यह आवश्यक है कि कम से कम "एक जीवित पड़ोसी की तरफ और दो कोनों पर" सेल का जन्म हो (यह नियम के रूप में लिखा गया है) बी 12)। नियम B12.4 / S2,3,4 ने अच्छे परिणाम दिए (कोण से 2 सेल स्थिति में पैदा होता है, एक तरफ - या किसी भी संयोजन में 4 जीवित पड़ोसियों के साथ, लेकिन 2,3,4 जीवित पड़ोसियों के साथ जीवित रहता है - फिर से, 3) किसी भी संयोजन में)। कई स्थिर आंकड़े थे, कई दिलचस्प पल्सर, और ग्लाइडर्स के बजाय, किसी तरह की "सदमे तरंगों" ने समय-समय पर उड़ान भरी। दुर्भाग्य से, जैसा कि प्रारंभिक घनत्व बढ़ता है, कॉन्फ़िगरेशन अराजक हो जाता है, और इसका घनत्व 1/3 पर रखा जाता है।
एक और दिलचस्प विन्यास है B12.21 / S3,4,6 (एक सेल का जन्म होता है, अगर उसके पास ठीक तीन जीवित पड़ोसी हों, और किनारे पर और कोने में रहने वाले पड़ोसी होने चाहिए और 3, 4 या 6 जीवित पड़ोसी हों)। इस दुनिया में कुछ स्थिर आंकड़े और पल्सर हैं, लेकिन कई ग्लाइडर हैं। वास्तव में, पूरे क्षेत्र में ग्लाइडर्स और उनके मलबे होते हैं (घनत्व 1/200 पर रखा जाता है), इसलिए वे लंबे समय तक नहीं रहते हैं।

अन्य निष्कर्ष

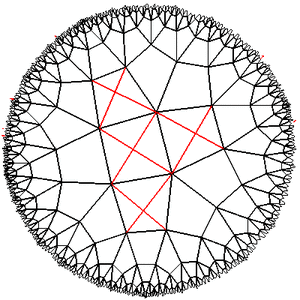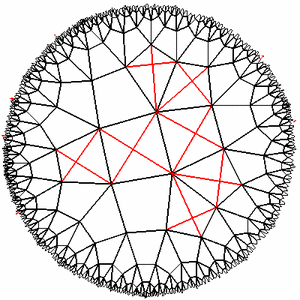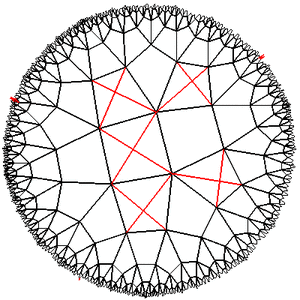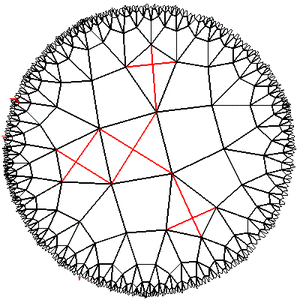
लोबाचेव्स्की विमान के प्रयोगों से पता चला कि यह वास्तव में आकार में बहुत छोटा है और क्षेत्र में बड़ा है। यदि आप कुछ कदमों से कुछ दूर जाते हैं, तो इसकी दृश्यता कम हो जाती है और यह पूरी तरह से अप्रभेद्यता को पूरा कर देगा, और वापस जाना बहुत मुश्किल होगा। यदि आप एक बाधा के चारों ओर जाने की कोशिश करते हैं, यहां तक ​​कि तथ्य यह है कि आप हर समय सही हो जाते हैं, तो गारंटी नहीं है कि आपका रास्ता बंद हो जाएगा (उदाहरण के लिए, यदि हम जाली {4,5} के वर्गों के साथ जाते हैं और हर दो बार 90 ग्राम मोड़ते हैं कदम, तो हम असीम दूर जाते हैं)। जीवित कोशिकाओं से भरे हुए क्षेत्रों के बीच संकीर्ण मुक्त अंतराल वाले क्षेत्र वास्तव में एक विशाल खाली स्थान बन सकते हैं, और जीवित कोशिकाओं के क्षेत्र, यदि आप दूर से देखते हैं, तो पूरी तरह से खाली क्षितिज पर एक छोटा सा स्थान होगा ...
सामान्य तौर पर, वस्तु दिलचस्प है।और अगर कोई फ्लैट खेल के मैदान से थक गया है, और आप तीन आयामी में नहीं जाना चाहते हैं, तो आप गेम को लॉबचेवस्की प्लेन के लैटिस में स्थानांतरित करने का प्रयास कर सकते हैं। अगर यह काम करता है तो क्या होगा?

ग्लाइडर स्पैन


श्रृंखला से एक विमान पर चलना "हम सभी मर जाते हैं"


ग्रिल पर खेल का एक टुकड़ा {5,4}