बहुत पहले नहीं, मैंने पहले ही
तथाकथित में खेल के लिए एआई के विकास पर एक
छोटी सी पोस्ट लिखी थी
। मिनी-शोगी , लेकिन
सर्वेक्षण से पता चला है कि विकास के बारे में अधिक संपूर्ण पोस्ट ह्रासोसॉइटी के लिए दिलचस्प होगी। बिल्ली के नीचे, कौन परवाह करता है।
बौद्धिक खेल खेल सकने वाले कार्यक्रमों का निर्माण एक बहुत ही दिलचस्प काम है, जिसमें बहुत व्यावहारिक और वैज्ञानिक मूल्य हैं।
बौद्धिक खेल (मुख्य रूप से शतरंज) खेलने के लिए मशीनें बनाने का पहला प्रयास कंप्यूटर के आगमन से बहुत पहले दिखाई दिया। 1769 के आसपास, प्रसिद्ध शतरंज मशीन "मैकेनिकल तुर्क" दिखाई दी। मशीन बहुत अच्छा खेली, लेकिन इसका पूरा रहस्य एक मजबूत शतरंज खिलाड़ी के अंदर छिपा था।
20 वीं शताब्दी में, यांत्रिक मशीनों ने डिजिटल कंप्यूटरों को रास्ता दिया। इस क्षेत्र में अग्रणी (कई अन्य लोगों के रूप में) को प्रसिद्ध गणितज्ञ एलन ट्यूरिंग कहा जा सकता है। आधुनिक मानकों के अनुसार, उन्होंने जो एल्गोरिथ्म विकसित किया वह बहुत ही आदिम था, और वास्तविक कंप्यूटर तक पहुंच की कमी के कारण, एल्गोरिथ्म को मैन्युअल रूप से निष्पादित करना आवश्यक था।
लगभग उसी समय, क्लाउड शैनन ने किसी भी स्थिति के लिए एक बेहतर कदम के अस्तित्व को सही ठहराया। उन्होंने अंतिम बोर्ड पर किसी भी खेल के लिए इस तरह का कदम खोजने के लिए एक एल्गोरिथ्म का प्रस्ताव दिया। दुर्भाग्य से, एक इष्टतम एल्गोरिथ्म के अस्तित्व के बावजूद, सीमित हार्डवेयर और समय संसाधनों के कारण इसका व्यावहारिक कार्यान्वयन असंभव है।
शैनन के समय से, बौद्धिक खेलों को प्रोग्रामिंग का कार्य मनोरंजन के क्षेत्र से गंभीर अनुसंधान के क्षेत्र में स्थानांतरित कर दिया गया है। हाल के वर्षों में शैनन के अध्ययन के आधार पर, व्यावहारिक एल्गोरिदम का निर्माण किया गया है, जिसकी मदद से कंप्यूटरों ने चेकर्स को सटीक रूप से खेलना सीखा है और शतरंज और जाने में उत्कृष्ट सफलता हासिल की है।
जापानी शोगी शतरंज उन कुछ खेलों में से एक है जहां एक व्यक्ति अभी भी कंप्यूटर से अधिक मजबूत है। सबसे पहले, यह खेल में उठाए गए आंकड़ों को वापस करने की संभावना के कारण है, यह नियम तेजी से संभव चाल की संख्या बढ़ाता है, जिसका अर्थ है कि यह खेल के विश्लेषण को जटिल करता है। यदि शतरंज में आप एक मनमानी स्थिति से लगभग 40 चालें बना सकते हैं, तो शोगी में संभावित चालों की संख्या सैकड़ों में मापी जाती है।
खेल के नियमशोगी खेलने के लिए एल्गोरिदम के निर्माण के बारे में बात करने से पहले, आपको इस खेल के नियमों का वर्णन करना होगा।
आंकड़ेशोगी में 8 अलग-अलग आंकड़े हैं (यदि आप उल्टे आंकड़ों को ध्यान में रखते हैं, तो 14)। विभिन्न टुकड़ों के लिए चाल के नियम तालिका में प्रस्तुत किए गए हैं:

यदि आप तालिका का विश्लेषण करते हैं, तो आप निम्नलिखित अवलोकन कर सकते हैं:
- शोगी में केवल दो लंबी दूरी के आंकड़े हैं: एक नाव और एक हाथी;
- कई आंकड़ों की पीछे हटने की संभावनाएं सीमित या पूरी तरह से अनुपस्थित हैं।
ये अवलोकन आपको सभी आंकड़ों को चार समूहों में विभाजित करने की अनुमति देते हैं:
- निरपेक्ष मूल्य का राजा;
- वरिष्ठ टुकड़े (बदमाश और बिशप), लंबी दूरी के हमलों और एक त्वरित वापसी में सक्षम;
- जनरलों (सोने और चांदी), जिनके आगे बढ़ने की संभावना पीछे हटने की संभावना से अधिक है;
- छोटे टुकड़े (घोड़ा, तीर, मोहरा), पीछे हटने में सक्षम नहीं।
प्रारंभिक प्लेसमेंट और चालों का क्रमदो खिलाड़ी शोगी खेलते हैं, जिन्हें आमतौर पर 9x9 वर्गों के वर्ग बोर्ड पर सेंटी (जाने के लिए पहला) और गोटे (दूसरा जाने वाला) कहा जाता है। आंकड़ों की प्रारंभिक व्यवस्था आंकड़े में दिखाई गई है:

प्रत्येक खिलाड़ी का एक विशेष स्टैंड (टीम) भी होता है, जहां प्रतिद्वंद्वी से लिए गए टुकड़े रखे जाते हैं। यह कहना भी प्रथागत है कि लिए गए आंकड़े "हाथ में" हैं।
तख्तापलटअंतिम तीन क्षैतिज (प्रत्येक खिलाड़ी के सापेक्ष) तख्तापलट क्षेत्र हैं। कोई भी अनकैप्ड टुकड़ा (सोने और राजा को छोड़कर) जो इस क्षेत्र के अंदर अपनी चाल शुरू या समाप्त करता है, पलट कर दूसरे टुकड़े में बदल सकता है। परिवर्तन नियम तय किए गए हैं और तालिका में दिखाए गए हैं:

यह नोट करना महत्वपूर्ण है कि खिलाड़ी यह तय करता है कि टुकड़ा को चालू करना है या नहीं। मामले जब एक तख्तापलट आवश्यक है निषिद्ध चाल अनुभाग में वर्णित हैं।
निर्वहनरीसेट नियम वह है जो मानवता द्वारा आविष्कृत सबसे कठिन खेलों में से एक शोगी गेम को बनाता है। नियम का सार यह है कि दुश्मन द्वारा खाए गए किसी भी आंकड़े को किसी भी स्वतंत्र क्षेत्र पर अपने रूप में रखा जा सकता है।
रीसेट नियम की कई सीमाएँ हैं, लेकिन वे काफी सरल हैं:
- सभी आंकड़े उलटे नहीं हैं (भले ही वे फ्लिप क्षेत्र में छोड़ दिए गए हों);
- आप ऊर्ध्वाधर पर एक मोहरा नहीं छोड़ सकते हैं जहां पहले से ही एक मोहरा है (एक टोकन को मोहरा नहीं माना जाता है);
- आप एक चेकमेट के साथ एक मोहरा मोड़ नहीं सकते।
निषिद्ध चालयदि प्रतिद्वंद्वी ने निषिद्ध कदम उठाया है, तो उसे तुरंत हार के रूप में गिना जाएगा, इसलिए निषिद्ध चालों की सूची जानना बेहद जरूरी है:
- चालें जो नियमों का उल्लंघन करती हैं (उदाहरण के लिए, सोने के विकर्ण);
- रीसेट नियमों का उल्लंघन (उदाहरण के लिए, ऊर्ध्वाधर के लिए दूसरा मोहरा रीसेट करना);
- एक चाल, जिसके बाद टुकड़ा एक भी कदम नहीं उठा सकता है। इस नियम में स्पष्टीकरण की आवश्यकता है। आप तख्तापलट के बिना आखिरी क्षैतिज तक मोहरे पर नहीं चल सकते हैं या तख्तापलट के बिना आखिरी या दंडनीय क्षैतिज रूप से शूरवीर हो सकते हैं। जाहिर है, आप इस तरह से आंकड़े रीसेट नहीं कर सकते।
राजा की जाँच के अधीन छोड़ने के साथ स्थिति पूरी तरह से स्पष्ट नहीं है। यदि खिलाड़ी ने अपने राजा को चेक का ध्यान नहीं दिया, तो अगला कदम राजा को खा सकता है (लेकिन ऐसा नहीं है)। इस मामले में, खेल खत्म माना जाता है।
खेल पूरा हुआखेल तब समाप्त होता है जब खिलाड़ियों में से कोई एक चेकआउट करता है या निषिद्ध कदम रखता है। लेकिन शोगी में खेल को समाप्त करने के लिए अतिरिक्त नियम हैं:
- यदि चेकर्स की एक निरंतर श्रृंखला (तथाकथित "अनन्त चेक") के परिणामस्वरूप स्थिति तीन बार दोहराई गई थी, तो चौथी बार हमलावर खिलाड़ी को एक और चाल चलनी चाहिए, अन्यथा उसे हार मान लिया जाएगा।
- यदि चेक की घोषणा किए बिना स्थिति 4 बार दोहराई गई थी, तो खिलाड़ी परिणामों की घोषणा किए बिना खेल को फिर से दोहराते हैं, लेकिन शेष समय के लिए एक रंग परिवर्तन के साथ।
उपरोक्त नियम शोगी के लिए अत्यंत दुर्लभ बनाते हैं (खेले गए सभी खेलों का 3% से अधिक नहीं)। फिर भी, एक मामले में एक ड्रॉ संभव है: यदि दोनों राजा दुश्मन के शिविर में घुस गए और वहां मजबूत हो गए। यदि दोनों खिलाड़ी सहमत हैं कि स्थिति गतिरोध है, तो स्कोरिंग किया जाता है। राजा को छोड़कर सभी टुकड़े (हाथ में), हाथी और किश्ती को 1 बिंदु पर, हाथी और किश्ती को छोड़कर, 5 बिंदुओं पर, राजा गणना में शामिल नहीं है।
पेशेवर खेलों में, 24 से कम अंक वाला खिलाड़ी हार जाता है, यदि दोनों खिलाड़ियों के पास कम से कम 24 अंक हैं, तो एक ड्रॉ घोषित किया जाता है। शौकिया खेलों में, विजेता कम से कम 27 अंकों के साथ एक है, अगर दोनों खिलाड़ियों के पास 27 अंक हैं, तो जीत को गोट से सम्मानित किया जाएगा।
सबसे अच्छा कदम खोजने के लिए एल्गोरिथ्ममिनीमैक्स एल्गोरिथमपहली बार, किसी भी स्थिति के लिए सबसे अच्छा कदम खोजने की रणनीति का वर्णन क्लाउड शैनन द्वारा किया गया था। यदि आप थोड़ा सोचते हैं, तो आप देख सकते हैं कि यह रणनीति काफी सरल है और किसी भी खेल के लिए लागू है।
आइए हम कुछ स्थिति रखते हैं जिसमें हमें एक इष्टतम कदम उठाने की आवश्यकता होती है। पहले आपको नियमों द्वारा अनुमत सभी चालें उत्पन्न करने की आवश्यकता है। फिर प्रत्येक सही चाल का मूल्यांकन किया जाना चाहिए। जीत की ओर ले जाने वाली चालों का मूल्यांकन +1 के रूप में किया जाएगा, जो -1 से हार के रूप में आगे बढ़ेगी, और ड्रॉ की ओर जाने वाली चालों को 0 का स्कोर प्राप्त होगा।
यह निर्धारित करने के लिए कि किस परिणाम को माना गया कदम हमें आगे ले जाएगा, हमें यह मान लेना चाहिए कि दुश्मन हर संभव तरीके से हमारे हर कदम का जवाब देगा। यानी वास्तव में, वह विचार के तहत एल्गोरिथ्म का उपयोग करेगा: वह अपनी सभी सही चालें उत्पन्न करेगा और उनमें से सबसे अच्छा एक का चयन करेगा, और यह आकलन करने के लिए कि उसकी चाल कितनी अच्छी है, वह यह मान लेगा कि हम सर्वोत्तम तरीके से जवाब देंगे, आदि।
यह पता चला है कि हमारे हिस्से में सबसे अच्छी चाल की खोज में, प्रतिद्वंद्वी से सबसे अच्छे उत्तर की खोज करने की प्रक्रिया को बुलाया जाएगा, जिसमें से प्रतिद्वंद्वी की प्रतिक्रिया के लिए हमारे सर्वोत्तम उत्तर की खोज करने की प्रक्रिया को बुलाया जाएगा, आदि।
सबसे अच्छा कदम के लिए खोज समारोह एक मैट या ड्रॉ की स्थिति होने तक खुद को पुन: कॉल करेगा।
इसके अलावा, अंतिम स्थिति का मूल्यांकन मुश्किल नहीं है, और जब माता-पिता नोड का मूल्यांकन करते हैं तो निम्नलिखित नियमों का उपयोग करते हैं:
- पहले खिलाड़ी के लिए कदम स्कोर की गणना बच्चे के नोड्स के अधिकतम स्कोर के रूप में की जाती है;
- दूसरे खिलाड़ी के लिए कदम स्कोर की गणना बच्चे के नोड्स के न्यूनतम स्कोर के रूप में की जाती है।
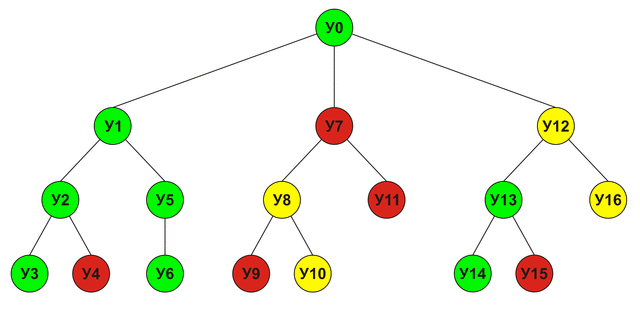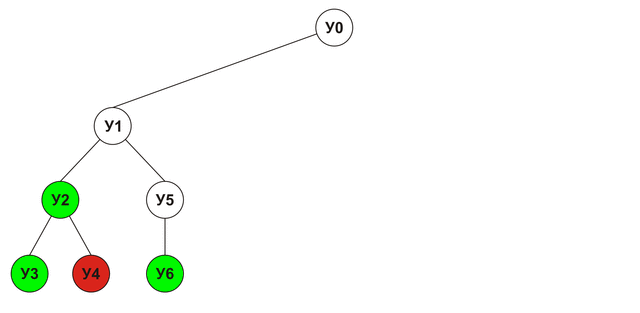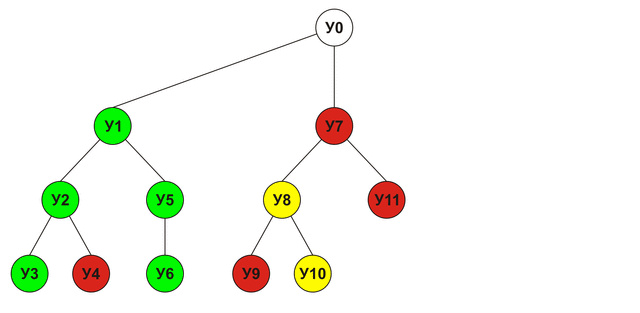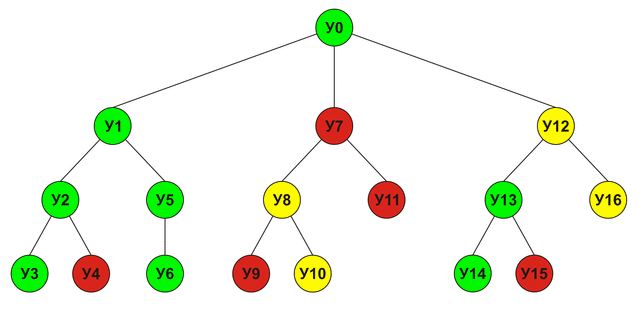
इस तरह के एक एल्गोरिथ्म को मिनीमैक्स कहा जाता है। यदि आप रेखांकन कॉल की एक श्रृंखला दर्शाते हैं, तो आपको तथाकथित मिलता है खेल का पेड़:

इस पेड़ में प्रत्येक नोड एक विश्लेषण की गई चाल का प्रतिनिधित्व करता है। एक नोड स्कोर उसके बच्चे के नोड्स के अधिकतम स्कोर के बराबर होगा। जिस क्रम में नोड्स का विश्लेषण किया जाएगा वह नीचे दिखाया गया है (हरा - विजय, लाल - हार, पीला - ड्रा):
 अल्फा-बीटा क्लिपिंग
अल्फा-बीटा क्लिपिंगउपरोक्त उदाहरण में, U0 नोड का अंतिम स्कोर प्राप्त करने के लिए, मुझे अन्य सभी नोड्स U1-U16 के लिए अनुमान प्राप्त करना था, लेकिन वास्तव में यह आवश्यक नहीं था: जैसे ही हमें पता चला कि नोड U1 जीत की ओर जाता है, नोड्स U7 का विश्लेषण करने की आवश्यकता U16 गायब हो जाता है, क्योंकि उन नोड्स के लिए प्राप्त कोई भी अनुमान U1 के अनुमान से अधिक नहीं होगा (क्योंकि यह अधिकतम है), जिसका अर्थ है कि यू 1 से बेहतर कोई चाल नहीं है। इसे देखते हुए, विश्लेषण किया गया पेड़ इस तरह दिखेगा:

जाहिर है, इस तरह के एक संक्षिप्त विश्लेषण समाधान की सटीकता को बिगड़ा नहीं है, लेकिन सबसे अच्छा कदम के लिए खोज समय को काफी कम कर देता है। यह "प्रूनिंग" का विचार है जो पेड़ की शाखाओं को अप्रकाशित करता है जो अल्फा-बीटा क्लिपिंग एल्गोरिथ्म को रेखांकित करता है।
कटऑफ का उपयोग करते समय, दो चर अतिरिक्त रूप से पेश किए जाते हैं: सेंटे (ए) के लिए एक न्यूनतम और गोट (बी) के लिए अधिकतम। अल्फा-बीटा कटऑफ एल्गोरिथ्म अपने आप में मिनीमैक्स एल्गोरिथ्म के समान है, सिवाय निम्नलिखित बिंदुओं के:
1. यदि किसी चाल का आकलन सीमा [A, B] के बाहर होता है, तो शाखा विश्लेषण को अनुसूची से आगे रोका जा सकता है, क्योंकि खिलाड़ियों को बेहतर स्थिति की ओर ले जाता है।
- यदि किसी भी क्षण पहले खिलाड़ी का स्कोर A से अधिक हो जाता है, तो A का मान अपडेट हो जाता है;
- वही दूसरे खिलाड़ी के लिए B के स्कोर के लिए जाता है।
इस एल्गोरिथ्म का उपयोग करते समय एक महत्वपूर्ण बिंदु वह क्रम है जिसमें चालों को देखा जाता है। यदि हम पहले उन चालों पर विचार करते हैं जो सबसे अधिक सीमा [ए, बी] को संकीर्ण करते हैं, तो कट शाखाओं की संख्या काफी बड़ी होगी। ऊपर दिए गए पेड़ पर लौटते हुए, यह नोटिस करना आसान है कि U7, U12, U1 का देखने का क्रम बहुत छोटा लाभ देगा। इसलिए, कट-ऑफ एल्गोरिदम का उपयोग करने से पहले, चालों को अपेक्षित दक्षता के अनुसार पूर्व-सॉर्ट किया जाता है।
बेशक, अग्रिम में यह जानना असंभव है कि कौन सा कदम सबसे अच्छा होगा, लेकिन कुछ नियम हैं। उदाहरण के लिए, मूव्स, चेकर्स, मूव्स जो किसी पोज़िशन को बेहतर बनाते हैं, आदि को अच्छा माना जाता है।
स्थिति मूल्यांकन समारोहऊपर वर्णित सभी एल्गोरिदम गेम ट्री को पूरी गहराई तक स्कैन करते हैं, लेकिन व्यावहारिक रूप से इस तरह के एल्गोरिदम को लागू करना असंभव है, इसलिए देखने की गहराई कृत्रिम रूप से सीमित है: पुनरावर्ती कॉल न केवल दोस्त और ड्रॉ के मामलों में समाप्त हो जाते हैं, बल्कि अधिकतम विश्लेषण गहराई तक पहुंचने पर भी। एक पेड़ को सीमित गहराई तक देखने वाले मैट अपेक्षाकृत दुर्लभ होते हैं, और सभी निमैटिक पदों को कुछ अनुमानी रेटिंग दी जानी होती है, जिसके लिए नीचे वर्णित विधियों का उपयोग किया जाता है।
सामग्री का मूल्यांकनअधिकांश शतरंज की तरह के खेल में, एक बहुत ही सटीक स्थिति का अनुमान सामग्री मूल्यांकन है। इस स्थिति में, प्रत्येक आकृति को एक निश्चित मान दिया जाता है, और खिलाड़ी के लिए स्थिति का अनुमान उसके टुकड़ों के योग और प्रतिद्वंद्वी के आंकड़ों के योग के बीच का अंतर होता है। शोगी सामग्री मूल्यांकन का भी उपयोग करता है, आंकड़ों की लागत की एक तालिका नीचे दिखाई गई है:

हाथ में सभी आंकड़े 30% अधिक अनुमानित हैं, क्योंकि निर्वहन की संभावना के कारण उनकी गतिशीलता काफी बढ़ जाती है।
कुछ स्पष्टीकरणों में राजा और टोकन की उच्च लागत की आवश्यकता होती है। राजा की इस तरह की उच्च लागत को इस तथ्य से समझाया जाता है कि राजा निरपेक्ष महत्व का है, पार्टी अपने नुकसान के साथ समाप्त होती है, इसलिए राजा को सभी अन्य टुकड़ों की तुलना में अधिक मूल्यवान माना जाता है। और टोकन की लागत इतनी अधिक है, क्योंकि टोकन एक्सचेंजों के लिए सबसे अच्छा आंकड़ा है: जब एक टोकन-सिल्वर का आदान-प्रदान होता है, तो एक खिलाड़ी सिल्वर जनरल के हाथ में प्राप्त करता है, और दूसरा खिलाड़ी सिर्फ एक मोहरा बन जाता है।
रणनीतिक मूल्यांकनरणनीतिक मूल्यांकन के महत्व के बारे में बात करने से पहले, एक बार फिर इस तथ्य पर ध्यान देना आवश्यक है कि टुकड़े कभी भी खेल को नहीं छोड़ते हैं और लिए गए सभी टुकड़े किसी भी समय वापस आ सकते हैं। यह तथ्य मूल रूप से स्थिति निर्धारण के दृष्टिकोण को बदल देता है।
सबसे पहले, शतरंज की तरह के खेल में बेहद प्रभावी होने वाला एक्सचेंज हेयरिज़ न केवल अप्रभावी हो जाता है, बल्कि हानिकारक भी होता है। यदि आप शतरंज में एक मोहरा जीतते हैं और लगातार समकक्ष एक्सचेंजों के लिए जाते हैं, तो एंडगेम में एक मोहरे में फायदा अक्सर निर्णायक होता है। शोगी में, इस तरह के आदान-प्रदान से आपके शिविर में दुश्मन के आंकड़े डंप हो सकते हैं।
दूसरे, शोगी के शिकार बहुत लोकप्रिय हैं। उदाहरण के लिए, एक खेल के अंत में, आपको अक्सर अपने हाथ में एक टुकड़ा पाने के लिए सोने के सामान्य या घोड़े के लिए एक पुराना टुकड़ा देना होगा जिसे आप चेकमेट कर सकते हैं या एक प्रभावी कांटा बना सकते हैं।
यदि आप देखते हैं कि इन दो स्थितियों में क्या समानता है, तो आप देख सकते हैं कि दुश्मन ने आपके टुकड़ों की खराब व्यवस्था का फायदा उठाया। ऐसे मामलों में, यह कहने के लिए प्रथागत है कि आंकड़ों का "बुरा आकार" है। शोगी में, प्रपत्र अक्सर भौतिक लाभ से अधिक महत्वपूर्ण होता है, इसलिए स्थिति का मूल्यांकन करते समय फॉर्म की विशेषताओं का मूल्यांकन किया जाना चाहिए। नीचे दिए गए आंकड़े खराब और अच्छे रूपों के उदाहरण दिखाते हैं (असुरक्षित जनरलों को लाल रंग में हाइलाइट किया गया है):

"अच्छे रूपों" के विचार का आगे का विकास किले हैं - राजा के लिए किलेबंदी, उसकी सुरक्षा सुनिश्चित करना और उसे शोहदों से बचाना। आम किले के उदाहरण तालिका में दिए गए हैं:

यह स्पष्ट है कि अच्छे रूपों को क्रमशः रणनीतिक मूल्यांकन के लिए एक निश्चित प्लस देना चाहिए, और खराब रूपों को क्रमशः मूल्यांकन को खराब करना चाहिए, लेकिन फॉर्म के अलावा बोर्ड के नियंत्रण को ध्यान में रखना भी आवश्यक है, उनके शत्रु राजा के लिए जनरलों की निकटता, बंद टुकड़ों की उपस्थिति, आदि।
उपरोक्त बातों को सारांशित करते हुए, यह एक बार फिर से ध्यान दिया जाना चाहिए कि किसी स्थिति का मूल्यांकन करने के कार्य में, न केवल सामग्री घटक, बल्कि रणनीतिक एक को भी ध्यान में रखना आवश्यक है।
कस्टम नवीकरण एल्गोरिथमपहले से ही माना जाने वाला मिनीमैक्स और अल्फा-बीटा क्लिपिंग एल्गोरिदम हमेशा किसी दिए गए गहराई पर सबसे अच्छी चाल पाते हैं, लेकिन समस्या यह है कि एक मजबूत गेम के लिए विश्लेषण गहराई (8-10 चाल) पर्याप्त नहीं है। पेशेवर 12-14 चालों और 20 से अधिक चालों के लिए कुछ पदों की गणना करते हैं। कंप्यूटर के लिए ऐसी गहराई अप्राप्य है।
कुछ समझौता विकल्प केवल पेड़ की कुछ शाखाओं को काफी गहराई से देखना है, जबकि शेष शाखाओं को कम गहराई तक देखा जाएगा। इस दृष्टिकोण को चयनात्मक नवीकरण कहा जाता है।
शतरंज के कार्यक्रमों में, शतरंज आम तौर पर लम्बा होता है, प्यादा अंतिम क्षैतिज और मजबूत कैद में चला जाता है। लेकिन शोगी में, यह दृष्टिकोण अप्रभावी है। यह एक निश्चित गहराई के बिना खोज करने का निर्णय लिया गया था, गहराई से कदम बढ़ाते हुए। इसके अलावा, सभी संभव चालों को सैद्धांतिक रूप से अलग-अलग गहराई पर माना जा सकता है, इसलिए आपको उस गहराई को याद रखना होगा जिसमें प्रत्येक चाल पर विचार किया गया था।
प्रारंभ में, प्रत्येक चाल के देखने की गहराई 0 है, और चाल स्कोर -INF (यानी, नुकसान) है। पहले पुनरावृत्ति पर, सभी चालों के लिए 1 की गहराई पर एक स्थिति विश्लेषण किया जाता है, प्रत्येक चाल की अपनी प्रभावशीलता रेटिंग प्राप्त होती है, और इसकी देखने की गहराई में 1. वृद्धि होती है। फिर सभी चालों को दक्षता से हल किया जाता है, और सबसे अच्छी चालों का विश्लेषण किया जाता है 2. यदि अगले विस्तार के दौरान यह पता चला कि अधिकतम स्कोर के साथ चाल का पहले से ही अधिकतम गहराई तक विश्लेषण किया गया है, फिर इस कदम को आगे के विचार से बाहर रखा गया है। गहरीकरण प्रक्रिया तब तक जारी रहती है जब तक सभी चालों को न्यूनतम गहराई तक नहीं देखा जाता है। नीचे दिया गया आंकड़ा चयनात्मक एक्सटेंशन (अधिकतम गहराई - 4, न्यूनतम गहराई - 2, नोड्स वर्तमान दृश्य गहराई पर अनुमानित स्थिति दिखाता है) का उपयोग करके एक पेड़ के निर्माण का अनुमानित क्रम दिखाता है:
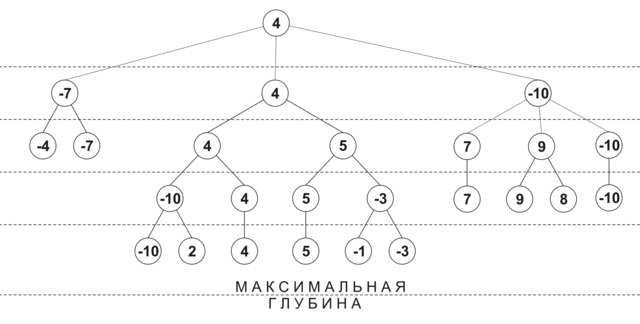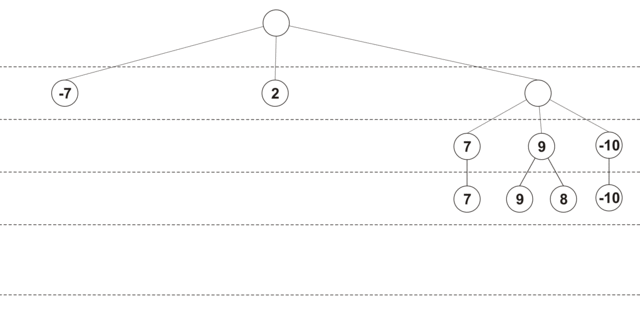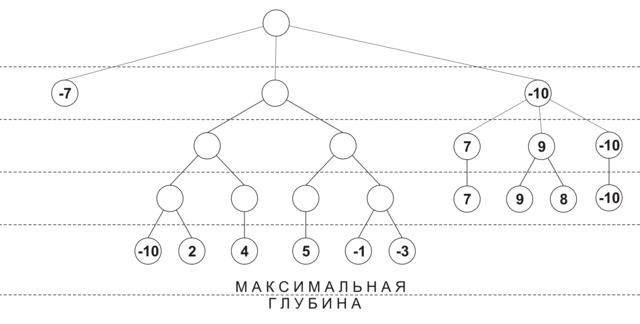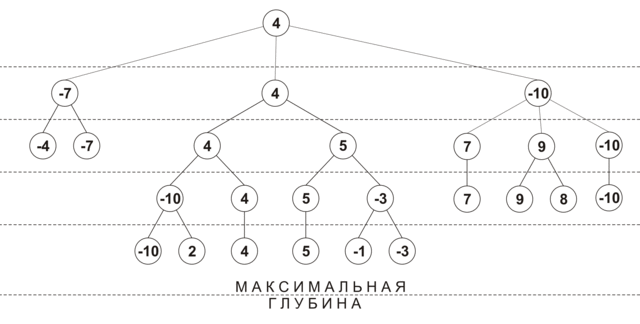
इस एल्गोरिथ्म का एक अतिरिक्त लाभ समय-सीमित गेम में इसकी प्रभावशीलता है: जब एक चाल के लिए आवंटित समय समाप्त हो जाता है, तो आप गणना किए गए परिणामों में से सबसे अच्छा वापस कर सकते हैं।
कैशिंगप्रोग्राम प्रदर्शन को बेहतर बनाने के लिए कैशिंग को सबसे प्रभावी तरीकों में से एक माना जाता है। गेमिंग एल्गोरिदम के निर्माण के संदर्भ में, पहले से ही विश्लेषण किए गए पदों की खोज के लिए कैशिंग का उपयोग किया जाता है।
वास्तव में, सर्वश्रेष्ठ चाल की खोज के दौरान, कुछ पदों को एक ही शाखा के भीतर दोहराया जा सकता है या पेड़ की विभिन्न शाखाओं में हो सकता है। एक क्लासिक एल्गोरिथ्म इस तरह की स्थिति पर फिर से विचार करेगा। इस तरह की कई गणना समग्र प्रदर्शन को काफी कम करती हैं। कैशिंग को बार-बार गणना करने की आवश्यकता को समाप्त करने के लिए डिज़ाइन किया गया है।
कैश में स्थिति की खोज उन पदों के हैश कार्यों के साथ स्थिति के हैश कार्यों की तुलना करने पर आधारित है जो पहले से ही कैश हिट कर चुके हैं। अधिकांश हैश फ़ंक्शंस की एक विशेषता टक्करों की उपस्थिति है (ऐसी स्थितियां जहां अलग-अलग इनपुट समान मूल्य देते हैं)। खेलों के लिए, हैश फ़ंक्शंस का यह व्यवहार अस्वीकार्य है, क्योंकि यहां तक कि स्थिति में सबसे छोटे बदलाव इष्टतम चाल को बहुत प्रभावित करते हैं। उपरोक्त को देखते हुए, एक स्ट्रिंग का उपयोग करने का निर्णय लिया गया था जो विशिष्ट रूप से एक हैश फ़ंक्शन के रूप में स्थिति का वर्णन करता है।
परिणामों के कैशिंग का उपयोग करने के लिए, सबसे अच्छा कदम खोजने के लिए एल्गोरिथ्म में निम्नलिखित परिवर्तन किए जाने चाहिए:
- मिसकॉल करने से पहले, कैश में एक स्थिति की उपलब्धता की जांच करें;
- यदि स्थिति कैश में है, तो गणना रोकें और पहले प्राप्त मूल्य वापस करें;
- मिसकॉल के अंत में, परिणाम को कैश में लिखें;
एक और सूक्ष्म बिंदु है। यदि कैश में पहले से ही वांछित स्थिति है, तो उथले गहराई पर गणना की जाती है, तो इस परिणाम का भी उपयोग किया जा सकता है। याद रखें कि अल्फा-बीटा कटऑफ एल्गोरिदम चालों के क्रम के प्रति बहुत संवेदनशील है। अभ्यास से पता चलता है कि उथले प्रतिपादन गहराई के साथ प्राप्त अनुमान चाल की गुणवत्ता का काफी उच्च गुणवत्ता वाला मूल्यांकन है। यानी
कैश में संग्रहीत मूल्यों का उपयोग अल्फा-बीटा कटऑफ को कॉल करने से पहले चाल को सॉर्ट करने के लिए किया जा सकता है।कैश का उपयोग करने की प्रभावशीलता का अनुमान निम्नलिखित ग्राफ का उपयोग करके लगाया जा सकता है, जो बार-बार कॉल के समय और संख्या के आधार पर स्थिति के मिसकॉल की गहराई की निर्भरता को दर्शाता है।
 ग्राफ से पता चलता है कि कैश का उपयोग बार-बार पदों के लिए प्रतिपादन गहराई को बढ़ाता है। उदाहरण के लिए, प्रति सेकंड 5 सेकंड की समय सीमा के साथ, कैश का उपयोग करने से आप कैश का उपयोग किए बिना 100-सेकंड के विश्लेषण के समान विश्लेषण गहराई प्राप्त कर सकते हैं।
ग्राफ से पता चलता है कि कैश का उपयोग बार-बार पदों के लिए प्रतिपादन गहराई को बढ़ाता है। उदाहरण के लिए, प्रति सेकंड 5 सेकंड की समय सीमा के साथ, कैश का उपयोग करने से आप कैश का उपयोग किए बिना 100-सेकंड के विश्लेषण के समान विश्लेषण गहराई प्राप्त कर सकते हैं।इस प्रकार
हम यह निष्कर्ष निकाल सकते हैं कि कैशिंग के उपयोग से विश्लेषण की गति में काफी वृद्धि होती है, लेकिन संसाधित वस्तुओं को संग्रहीत करने के लिए महत्वपूर्ण मात्रा में मेमोरी की आवश्यकता होती है।और निष्कर्ष के रूप में, शोगी लवल कार्यक्रम के खिलाफ कार्यक्रम द्वारा विकसित खेल का एक छोटा सा उदाहरण। 100: