जावा में हैशकोड () कार्यान्वयन पर नोट्स

अक्सर साक्षात्कार के दौरान आपको हैशकोड () फ़ंक्शन के बारे में पूछना पड़ता है।
मैं यहां इस फ़ंक्शन के सभी गुणों और किसी अन्य के साथ इसके कनेक्शन की सूची नहीं दूंगा, कोई कम महत्वपूर्ण फ़ंक्शन बराबर नहीं ()। यह जानकारी सभी जावा पाठ्यपुस्तकों में है और मुझे यहाँ इसे दोहराने का कोई कारण नहीं दिखता है। मैं केवल एक ही संपत्ति पर रहना चाहता हूं: हैशकोड को समान रूप से फ़ंक्शन वैल्यू रेंज पर वितरित किया जाना चाहिए। मैंने सोचा: "समान वितरण की गारंटी क्या है?"

आगे देखते हुए, मैं कहता हूँ कि मैं काफी दिलचस्प निष्कर्ष पर आया हूँ। अगर मुझे कहीं तर्क करने में गलती हुई तो मैं इसे सुधारना चाहूंगा।

हम गुरु से पूछेंगे

सबसे पहले, मैंने Object.hashCode () पर जावा डॉक्यूमेंट को चालू करने का निर्णय लिया। जैसा कि सभी देख सकते हैं, ऐसी कोई जानकारी नहीं है जो हमें रुचती है। उसके बाद मैं गुरु के पास गया। ब्रूस एकेल ने बलोच पर सिर हिलाते हुए 5 पृष्ठ लिखे (अधिक सटीक, उनसे कॉपी किए गए), लाइनों के साथ एक उदाहरण दिया, और अंत में उन्होंने "उपयोगी पुस्तकालयों" का उपयोग करने का सुझाव दिया। जोशुआ बलोच ने बेहतर किया: उन्होंने एक गणना एल्गोरिथ्म का प्रस्ताव दिया, जिसमें अपराधों के लाभों के बारे में बात की और ... एक उदाहरण भी दिया। मैं मदद नहीं कर सकता लेकिन बोली:

गुणक 37 को इसलिए चुना गया क्योंकि यह एक अजीब प्राइम है। ... अभाज्य संख्या का उपयोग करने के फायदे कम स्पष्ट हैं, लेकिन इस उद्देश्य के लिए primes का उपयोग करना पारंपरिक है।

किसी भी लेखक ने उपरोक्त एल्गोरिथम का विश्लेषण करने और इसकी शुद्धता को साबित करने की जहमत नहीं उठाई।

एल्गोरिथ्म (मुक्त रीटेलिंग में)

1) उदाहरण के लिए, शून्य के अलावा एक नंबर लें। 17. सुविधा के लिए, हम इसे पी कहते हैं। इस प्रारंभिक मूल्य (परिणाम = पी) के लिए चर परिणाम असाइन करें।
2) प्रत्येक क्षेत्र के लिए, कुछ नियमों के अनुसार हैशकोड सी की गणना करें। ये नियम, अब हम बहुत रुचि नहीं रखते हैं, वे परिणाम को प्रभावित नहीं करते हैं। सादगी के लिए, हम पूर्णांक (int) के साथ काम करेंगे और हम हैशकोड को संख्या के मान के बराबर ले लेंगे ...
3) परिणाम और परिणामी हैशकोड के साथ मिलाएं: परिणाम = परिणाम * q + c, जहां q = 37, क्योंकि, जैसा कि हम याद करते हैं, यह विषम और सरल है।
4) परिणाम लौटाएं।

एल्गोरिथम विश्लेषण

सबसे पहले, हम कुछ धारणाएँ बनाते हैं:
1) जैसा कि पहले ही ऊपर उल्लेख किया गया है, हम पूर्णांक के साथ काम करेंगे।
2) हम मानते हैं कि हैशकोड 0 से 2 ³² तक मान लेता है। यही है, हम नकारात्मक मूल्यों के साथ काम नहीं करेंगे।
3) हम मानते हैं कि गुणा और जोड़ के दौरान अतिप्रवाह नहीं होता है। हम केवल छोटे प्रारंभिक मूल्यों का उपयोग करेंगे।
4) हम मानते हैं कि हैशकोड बनाया गया है जिसके आधार पर डेटा समान रूप से वितरित किया जाता है।

अधिक विशिष्ट होने के लिए, मैं दो-आयामी अंतरिक्ष में एक विमान पर पूर्णांक निर्देशांक (x, y) के साथ बिंदुओं पर विचार करूंगा, बशर्ते कि x> = 0, y> = 0।

हम बिंदु P1 (X1, y1) के लिए हैश फ़ंक्शन लिखते हैं:

(p * q + X1) * q + y1 = h

h फ़ंक्शन का हैश मान है।
अब मैं कुछ अन्य बिंदु P2 (x2, y2) पर विचार करना चाहता हूं जिसमें समान हैश फ़ंक्शन होगा। यही है, यह सिर्फ टक्कर का मामला है:

(p * q + x2) * q + y2 = h

पहली से दूसरी अभिव्यक्ति घटाना:

q (X1-x2) + y1 - y2 = 0 (ध्यान दें कि घटाव के बाद p युक्त कारक खो जाता है)

Q को दाईं ओर ले जाएं:

(X1 - x2) / (y2-y1) = q (यह स्पष्ट है कि हर एक गैर-शून्य होना चाहिए)

यदि हम ऐसे मानों का चयन करते हैं X1, x2, y1, y2 कि प्राप्त समानता पूरी हो गई है, तो ये निर्देशांक उस फ़ंक्शन के हैश तर्क के मूल्यों के अनुरूप होंगे, जिस पर टक्कर होती है।

आप इस विकल्प की पेशकश कर सकते हैं:

X1 = 38
x2 = 1
y2 = 2
y1 = 1

यही है, अंक P (38, 1) और P (1, 2) का समान हैशकोड है ... मैंने सोचा था कि हैश कोड के लिए 4 बिलियन संभावित मूल्यों के साथ, 100x100 वर्ग में भी टकराव से बचा जा सकता है!

अब, ऐसे एन वेरिएबल्स के मामले पर विचार करें, जो स्वतंत्र रूप से 0 से कुछ एम तक भिन्न होते हैं। मैं एम का अधिकतम मूल्य ज्ञात करना चाहता हूं, ताकि अच्छी तरह से लिखे गए हैशकोड फ़ंक्शन के अंतराल में 0 से एम तक सभी एन वेरिएबल्स में टकराव न हो। कुछ विचार-विमर्श के बाद, हमें M के लिए मान मिलता है:

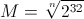
विमान एम पर बिंदुओं के मामले के लिए, यह मूल्य 65536 लेता है।

ऐसा लगता है कि बलोच द्वारा दिया गया सूत्र 8 या अधिक चर के मामले के लिए हैश कोड का एक स्वीकार्य वितरण देगा।

अब तीन-आयामी अंतरिक्ष में बिंदुओं पर विचार करें। हम एक छोटा सा कार्यक्रम लिखेंगे कि एक ट्रिपल चक्र में 0 से 100 तक अंक (कुल में एक मिलियन अंक) पर पुनरावृत्त होते हैं और टकराव की संख्या को गिनते हैं। इस कार्यक्रम का कोड प्राथमिक है, इसलिए मैंने इसे यहां नहीं दिया। परिणाम दिलचस्प है: मुझे 901692 टक्कर मिलीं! यह 90% से थोड़ा अधिक है। यह पता चला है कि बलोच, हैश फ़ंक्शन की आड़ में, टकराव प्राप्त करने के लिए एक समारोह प्रस्तावित करता है?

दो चर के लिए अच्छा हैशकोड

अब दो चर (X1, y1) के मामले के लिए एक अच्छा एल्गोरिथ्म बनाने की कोशिश करते हैं। संख्यात्मक विमान पर X1 और y1 के मूल्यों को समान रूप से बिखेरने के लिए, हम गुणा का उपयोग करते हैं: हम X1 को कुछ संख्या p से गुणा करते हैं, और q द्वारा y1 करते हैं। अभी के लिए, हम p और q पर कोई शर्त नहीं लगाते हैं। किसी फ़ंक्शन का हैश मान प्राप्त करने के लिए, इन उत्पादों को जोड़ें:

p * X1 + q * y1 = h

हम ऊपर वर्णित तकनीक का उपयोग करते हैं: x2, y2, जैसे कि फ़ंक्शन का हैश मान टकराव पैदा करता है।

p * x2 + q * y2 = h

पहली समानता से दूसरे को घटाएं:

p * (X1-x2) + q (y1-y2) = 0
या
(X1-x2) / (y2-y1) = q / p (बशर्ते कि भाजक शून्य के बराबर न हो)

यदि q को 37 के बराबर लिया जाता है, और p - 1, तो हम बलोच से एक सूत्र प्राप्त करते हैं।
अंतिम सूत्र से और इस तथ्य से कि हम पूर्णांक के साथ काम करते हैं, यह निम्नानुसार है:
1) अंतर (X1-x2) q के समानुपाती होता है, अंतर (y2-y1) p के समानुपाती होता है।
2) जितना बड़ा p और q, बिंदुओं के बीच की दूरी उतनी अधिक हो सकती है।
3) p और q कोप्रेम होना चाहिए।
4) h = 2 ³² पर ऊपरी सीमा होने पर, हम यह प्राप्त करते हैं कि प्रत्येक उत्पाद p * X1, q * y1 2 ^32/2 से कम होना चाहिए। यह निम्नानुसार है कि पी और क्यू 32768 से कम होना चाहिए। उदाहरण के लिए, 32765 और 32767। यहां हमें अपनी धारणा को याद रखना चाहिए: हम केवल सकारात्मक संख्याओं के साथ काम करते हैं। जब इसके अलावा एक अतिप्रवाह होता है, तो हम खुद को संख्यात्मक अक्ष के नकारात्मक भाग में पाते हैं। मैं पाठकों को सुझाव देता हूं कि वे इस पर विचार करें

निष्कर्ष

जैसा कि डोनाल्ड नुथ ने छद्म यादृच्छिक अनुक्रम जनरेटर पर अध्याय में लिखा था, अगर एल्गोरिथ्म जटिल और भ्रमित दिखता है, इसका मतलब यह नहीं है कि यह सही तरीके से काम करता है (संक्षिप्त विवरण)।

जोशुआ बलोच से हैश फ़ंक्शन के कार्यान्वयन का उपयोग करते हैं, लेकिन बड़ी संख्या में हैशेड चर होते हैं, वे शांति से सो सकते हैं। इसके अलावा, जिनके पास विभिन्न प्रकार के हैश संग्रह हैं, वे एक प्रदर्शन अड़चन नहीं हैं।

यदि आप अपने कोड के प्रदर्शन के लिए संघर्ष कर रहे हैं, सभी संभावित trifles को ध्यान में रखते हुए, तो आपको संभवतः अपने हैशकोड () कार्यान्वयन पर एक नया नज़र रखना चाहिए। यह देखते हुए कि हैशेड मान आपके विशिष्ट व्यावसायिक क्षेत्र के लिए समान रूप से वितरित नहीं किया जा सकता है, आप किसी भी उत्पन्न विकल्प की तुलना में हैश कोड के बेहतर वितरण के साथ एक हैश फ़ंक्शन लिख सकते हैं। जब आप हैशकोड () को फिर से लिखते हैं, तो आपको बराबरी देखने की ज़रूरत हो सकती है (): हो सकता है कि आप कम जाँच के बाद गलत मान लौटा सकें।

अंत तक पढ़ने वालों को धन्यवाद।

संदर्भ:
ब्रूस एकेल "जावा तीसरे संस्करण में सोच"
यहोशू बलोच "प्रभावी जावा: प्रोग्रामिंग भाषा गाइड"