बायेसियन विधियों का परिचय

एक परिचय के रूप में

वर्तमान में, बायेसियन विधियां काफी व्यापक हैं और ज्ञान के विभिन्न क्षेत्रों में सक्रिय रूप से उपयोग की जाती हैं। हालांकि, दुर्भाग्य से, बहुत से लोगों को इस बात का अंदाजा नहीं है कि यह क्या है और इसकी आवश्यकता क्यों है। कारणों में से एक रूसी में बड़ी मात्रा में साहित्य की कमी है। इसलिए, यहां मैं उनके सिद्धांतों को यथासंभव सरल बनाने की कोशिश करूंगा, शुरुआत से ही (मैं माफी मांगता हूं अगर यह किसी को बहुत सरल लगता है)।

भविष्य में, मैं सीधे बायेसियन विश्लेषण पर जाना चाहूंगा और वास्तविक डेटा को संसाधित करने के बारे में बात करूंगा और, मेरी राय में, आर भाषा का एक उत्कृष्ट विकल्प ( यहां थोड़ा इसके बारे में लिखा गया था) - अजगर मॉड्यूल के साथ पायथन। निजी तौर पर, पायथन मुझे JAGS और BUGS पैकेज के साथ R की तुलना में बहुत अधिक समझ और तार्किक लगता है, इसके अलावा, पायथन बहुत अधिक स्वतंत्रता और लचीलापन देता है (हालाँकि पायथन की अपनी कठिनाइयाँ हैं, लेकिन वे अचूक हैं, और वे सरल विश्लेषण में आम नहीं हैं। )।

थोड़ा इतिहास

एक संक्षिप्त ऐतिहासिक संदर्भ के रूप में, मैं कहूंगा कि बेयस सूत्र अपने लेखक, थॉमस बेयस की मृत्यु के बाद 1763 2 साल पहले ही प्रकाशित हुआ था। हालांकि, इसका उपयोग करने के तरीके वास्तव में केवल बीसवीं शताब्दी के अंत तक व्यापक थे। ऐसा इसलिए है क्योंकि गणना के लिए कुछ कम्प्यूटेशनल लागतों की आवश्यकता होती है, और वे केवल सूचना प्रौद्योगिकी के विकास के साथ संभव हो गए।

संभावना और बेयस प्रमेय पर

बेयस फॉर्मूला और बाद के सभी एक्सपोजर में संभावना की समझ की आवश्यकता होती है। आप विकिपीडिया पर संभाव्यता के बारे में अधिक पढ़ सकते हैं।
व्यवहार में, किसी घटना के घटित होने की संभावना इस घटना के घटने की आवृत्ति है, अर्थात्, किसी घटना की टिप्पणियों की संख्या का अनुपात बड़े (सैद्धांतिक रूप से अनंत) टिप्पणियों की कुल संख्या के साथ।
निम्नलिखित प्रयोग पर विचार करें: हम अंतराल से किसी भी संख्या को कहते हैं [0, 1] और देखें कि यह संख्या बीच में है, उदाहरण के लिए, 0.1 और 0.4। जैसा कि आप अनुमान लगा सकते हैं, इस घटना की संभावना सेगमेंट की लंबाई के अनुपात के बराबर होगी [0.1, 0.4] सेगमेंट की कुल लंबाई [0, 1] (दूसरे शब्दों में, मूल्यों की कुल "संख्या" के समान रूप से संभावित समान मानों की "संख्या" का अनुपात), (0.4) - 0.1) / (1 - 0) = 0.3, अर्थात, खंड में गिरने की संभावना [0.1, 0.4] 30% है।

अब चलो वर्ग [0, 1] x [0, 1] को देखें।


मान लीजिए कि हमें संख्याओं (x, y) के जोड़ों का नाम देना चाहिए, जिनमें से प्रत्येक शून्य से अधिक और एकता से कम है। संभावना है कि x (पहली संख्या) सीमा [0.1, 0.4] के भीतर होगी (पहले क्षेत्र में एक नीले क्षेत्र के रूप में दिखाया गया है, इस समय दूसरा नंबर y हमारे लिए महत्वपूर्ण नहीं है) पूरे वर्ग के क्षेत्र के लिए नीले क्षेत्र के क्षेत्र के अनुपात के बराबर है, फिर वहाँ (0.4 - 0.1) * (1 - 0) / (1 * 1) = 0.3, यानी 30% है। इस प्रकार, हम लिख सकते हैं कि x [खंड 0.1, 0.4] से संबंधित संभावना p (0.1 <= x <= 0.4) = 0.3 है या संक्षिप्तता, पी (एक्स) = 0.3 के लिए।
यदि हम अब y को देखते हैं, तो, इसी तरह, संभावना है कि y, अंतराल के अंदर है [0.5, 0.7] पूरे वर्ग p (0.5 <= y <= 0.7 = 0.2, या संक्षिप्तता p) के क्षेत्र के लिए हरे क्षेत्र के क्षेत्रफल के अनुपात के बराबर है। (य) = ०.२।
अब देखते हैं कि हम एक ही समय में x और y के मूल्यों के बारे में क्या सीख सकते हैं।
यदि हम यह जानना चाहते हैं कि एक्स और वाई दोनों संबंधित सेगमेंट में क्या संभावना है, तो हमें अंधेरे क्षेत्र (हरे और नीले क्षेत्रों के चौराहे) के अनुपात की गणना पूरे वर्ग के क्षेत्र में करने की आवश्यकता है: पी (एक्स, वाई = = (0.4 - 0.1) ) * (0.7 - 0.5) / (1 * 1) = 0.06

अब मान लें कि हम जानना चाहते हैं कि y, अंतराल [0.5, 0.7] में क्या संभावना है अगर x पहले से ही अंतराल [0.1, 0.4] में है। यही है, वास्तव में, हमारे पास एक फ़िल्टर है और जब हम जोड़े (x, y) कहते हैं, तो हम उन जोड़ियों को तुरंत त्याग देते हैं जो इस शर्त को संतुष्ट नहीं करते हैं कि x दिए गए अंतराल में है, और फिर फ़िल्टर किए गए जोड़ों में से हम उन पर विचार करते हैं जिनके लिए y हमारी स्थिति को संतुष्ट करते हैं और हम संभाव्यता को उन युग्मों की संख्या के अनुपात के रूप में मानते हैं जिनके लिए y उक्त अंतराल में फ़िल्टर्ड जोड़े की कुल संख्या में निहित है (यानी, जिसके लिए x अंतराल में निहित है [0.1, 0.4])। हम इस संभाव्यता को p (Y | X) के रूप में लिख सकते हैं। जाहिर है, यह संभावना अंधेरे क्षेत्र (हरे और नीले क्षेत्रों के चौराहे) के क्षेत्रफल के अनुपात के बराबर है। अंधेरे क्षेत्र का क्षेत्र (0.4 - 0.1) * (0.7 - 0.5) = 0.06 है, और नीले रंग का क्षेत्र है (0.4 - 0.1) * (1 - 0) = 0.3, तो उनका अनुपात 0.06 / 0.3 = 0.2 है। दूसरे शब्दों में, खंड x पर y को खोजने की संभावना [0.5, 0.7] दी गई है जो x पहले से ही खंड से संबंधित है [0.1, 0.4] p (Y | X) = 0.2 है।
आप देख सकते हैं कि, उपरोक्त सभी और उपरोक्त सभी संकेतन को ध्यान में रखते हुए, हम निम्नलिखित अभिव्यक्ति लिख सकते हैं
p (Y | X) = p (X, Y) / p (X)

पी (एक्स। वाई) के संबंध में हमें पिछले सभी तर्क संक्षिप्त रूप से बताएं: हम जोड़े (एक्स, वाई) कहते हैं और उन फिल्टर करते हैं जिनके लिए y 0.5 और 0.7 के बीच है, तो संभावना है कि x अंतराल में है [0.1, 0.4] ] बशर्ते कि y खंड [0.5, 0.7] के अंतर्गत आता है, जो अंधेरे क्षेत्र के हरे रंग के क्षेत्र के अनुपात के बराबर है:
p (X | Y) = p (X, Y) / p (Y)

उपरोक्त दो सूत्रों में, हम देखते हैं कि शब्द p (X, Y) समान है, और हम इसे बाहर कर सकते हैं:

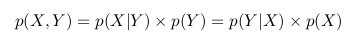
हम अंतिम समानता को फिर से लिख सकते हैं


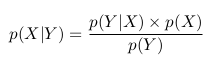
यह बेयस का प्रमेय है।
यह भी ध्यान रखना दिलचस्प है कि पी (वाई) वास्तव में एक्स के सभी मूल्यों के लिए पी (एक्स, वाई) है। अर्थात, यदि हम अंधेरे क्षेत्र को लेते हैं और इसे खींचते हैं ताकि यह एक्स के सभी मूल्यों को कवर करे, तो यह बिल्कुल हरे क्षेत्र को दोहराएगा। , जिसका अर्थ है कि यह p (Y) के बराबर होगा। गणित की भाषा में, इसका मतलब निम्न होगा:
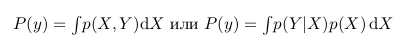
फिर हम निम्न रूप में बेयस सूत्र को फिर से लिख सकते हैं:

Bayes प्रमेय के अनुप्रयोग

आइए निम्नलिखित उदाहरण देखें। एक सिक्का लें और इसे 3 बार टॉस करें। उसी संभावना के साथ, हम निम्नलिखित परिणाम (ओ - ईगल, पी - पूंछ) प्राप्त कर सकते हैं: एलएलसी, ओओआर, ओआरओ, ओआरआर, आरओओ, आरओआर, पीपीओ, पीपीपी।

हम गणना कर सकते हैं कि प्रत्येक मामले में कितने ईगल गिरे और सिर-पूंछ, पूंछ-ईगल कितने परिवर्तन हुए:


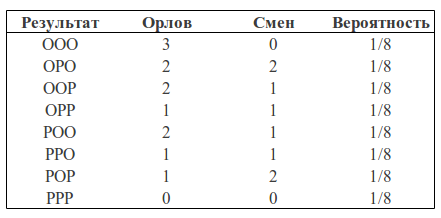
हम ईगल की संख्या और परिवर्तनों की संख्या को दो यादृच्छिक चर के रूप में मान सकते हैं। तब प्रायिकता तालिका के निम्न रूप होंगे:


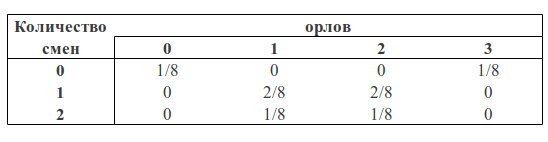
अब हम कार्रवाई में बेयस सूत्र देख सकते हैं।
लेकिन पहले, हम वर्ग के साथ एक सादृश्य आकर्षित करते हैं, जिसे हमने पहले माना था।
आप देख सकते हैं कि p (1O) तीसरे स्तंभ (वर्ग का "नीला क्षेत्र) का योग है और इस स्तंभ के सभी सेल मानों के योग के बराबर है: p (1O) = 2/8 + 1/8 = 3/8
p (1) तीसरी पंक्ति (वर्ग का "हरा क्षेत्र) का योग है और इसी तरह, इस पंक्ति p (1) = 2/8 + 2/8 = 4/8 में सभी सेल मानों के योग के बराबर है।
संभावना है कि हमें एक ईगल मिला है और एक शिफ्ट इन क्षेत्रों के चौराहे के बराबर है (यानी, तीसरे कॉलम और तीसरी पंक्ति के चौराहे की सेल में मान) p (1C, 1O) = 2/8
फिर, ऊपर वर्णित सूत्रों का अनुसरण करते हुए, हम एक बदलाव की संभावना की गणना कर सकते हैं यदि हमें तीन चड्डी में एक ईगल मिला:
p (1C | 1O) = p (1C, 1O) / p (1O) = (2/8) / (3/8) = 2/3
या एक ईगल मिलने की संभावना अगर हमें एक शिफ्ट में मिली:
p (1 | 1) = p (1, 1) / p (1) = (2/8) / (4/8) = 1/2
यदि हम एक ईगल पी की उपस्थिति में एक शिफ्ट होने की संभावना की गणना करते हैं (बे 1 सूत्र) के माध्यम से एक (1 | 1 एस), तो हम प्राप्त करते हैं:
p (1 | 1) = p (1 1 1 | 1) * p (1) / p (1) = (2/3) * (3/8) / (4/8) = 1/2
हमें ऊपर क्या मिला।

लेकिन उपरोक्त उदाहरण का क्या व्यावहारिक महत्व है?
तथ्य यह है कि जब हम वास्तविक डेटा का विश्लेषण करते हैं, आमतौर पर हम इन डेटा के कुछ पैरामीटर में रुचि रखते हैं (उदाहरण के लिए, औसत, विचरण, आदि)। फिर हम निम्नलिखित संभावना तालिका के साथ निम्नलिखित सादृश्य आकर्षित कर सकते हैं: पंक्तियों को हमारे प्रयोगात्मक डेटा (उन्हें डेटा निरूपित करें) दें, और स्तंभों को इन डेटा के लिए ब्याज के पैरामीटर के संभावित मान होने दें (इसे निरूपित करें )। तब हम उपलब्ध डेटा के आधार पर पैरामीटर का एक निश्चित मूल्य प्राप्त करने की संभावना में रुचि रखते हैं ।
हम बेयस फॉर्मूला लागू कर सकते हैं और निम्नलिखित लिख सकते हैं:

और अभिन्न के साथ सूत्र को याद करते हुए, हम निम्नलिखित लिख सकते हैं:


यही है, वास्तव में, हमारे विश्लेषण के परिणामस्वरूप, हमारे पास पैरामीटर के एक फ़ंक्शन के रूप में संभावना है। अब, हम उदाहरण के लिए, इस फ़ंक्शन को अधिकतम कर सकते हैं और सबसे संभावित पैरामीटर मान प्राप्त कर सकते हैं, विचरण और औसत पैरामीटर मान की गणना कर सकते हैं, उस सेगमेंट की सीमाओं की गणना करते हैं जिसके भीतर ब्याज का पैरामीटर 95% की संभावना के साथ निहित है, आदि।

संभावना जिसे बाद की संभावना कहा जाता है। और इसकी गणना करने के लिए, हमारे पास होना चाहिए
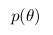
- संभावना समारोह और - एक प्राथमिकता संभावना।
संभावना समारोह हमारे मॉडल द्वारा निर्धारित किया जाता है। यही है, हम एक डेटा संग्रह मॉडल बना रहे हैं जो हमारे लिए ब्याज के पैरामीटर पर निर्भर करता है। उदाहरण के लिए, हम स्ट्रेट लाइन y = a * x + b का उपयोग करके डेटा को इंटरपोल करना चाहते हैं (इसलिए हम यह मानते हैं कि सभी डेटा का गौसियन शोर के साथ एक रैखिक संबंध है जो एक ज्ञात फैलाव के साथ इस पर आरोपित है)। तब ए और बी हमारे पैरामीटर हैं, और हम उनके सबसे संभावित मूल्यों का पता लगाना चाहते हैं, और संभावना फ़ंक्शन लाइन के समीकरण और इस फैलाव द्वारा दिए गए औसत के साथ एक गौसियन है।
एक प्राथमिकता संभावना में वह जानकारी शामिल होती है जिसे हम विश्लेषण से पहले जानते हैं। उदाहरण के लिए, हम यह सुनिश्चित करने के लिए जानते हैं कि लाइन में एक सकारात्मक ढलान होना चाहिए, या कि एक्स अक्ष के साथ चौराहे के बिंदु पर मूल्य सकारात्मक होना चाहिए - यह सब और न केवल हम अपने विश्लेषण में शामिल कर सकते हैं।
जैसा कि आप देख सकते हैं, अंश का भाजक एक अभिन्न है (या मामले में जब पैरामीटर पैरामीटर के सभी संभावित मूल्यों पर अंश के योग से केवल कुछ असतत मान ले सकते हैं)। व्यवहार में, इसका मतलब यह है कि भाजक स्थिर है और पीछे की संभावना को सामान्य करने के लिए कार्य करता है (अर्थात, ताकि पूर्ववर्ती संभावना का एकीकरण एकता के बराबर हो)।

इस पर, मैं अपनी पोस्ट ( यहां जारी) खत्म करना चाहूंगा। मुझे आपकी टिप्पणियों पर खुशी होगी।