Habré पर विशेष रूप से सामान्य और आनुवंशिक एल्गोरिदम में विकासवादी एल्गोरिदम पर कई लेख हैं। इस तरह के लेख आमतौर पर आनुवंशिक एल्गोरिथ्म की सामान्य संरचना और विचारधारा को अधिक या कम विवरण में वर्णित करते हैं, और फिर इसके उपयोग का एक उदाहरण देते हैं। इस तरह के प्रत्येक उदाहरण में व्यक्तियों द्वारा पार करने की प्रक्रिया के कुछ संस्करण शामिल हैं, म्यूटेशन और लेखक द्वारा चुने गए चयन, और ज्यादातर मामलों में, प्रत्येक नए कार्य के लिए, आपको इन प्रक्रियाओं के अपने स्वयं के संस्करण के साथ आना होगा। वैसे, यहां तक कि जीन वेक्टर द्वारा निर्णय स्थान के तत्व का प्रतिनिधित्व करने का विकल्प परिणामी एल्गोरिदम की गुणवत्ता को बहुत प्रभावित करता है और अनिवार्य रूप से एक कला है।
इसी समय, वास्तविक चर के न्यूनतम
n को खोजने की अनुकूलन समस्या के लिए बहुत सारी व्यावहारिक समस्याओं को आसानी से कम किया जा सकता है, और इस प्रकार के संस्करण के लिए मैं एक तैयार-विश्वसनीय विश्वसनीय आनुवंशिक एल्गोरिथ्म करना चाहूंगा। चूँकि वास्तविक संख्या वाले वैक्टर के लिए क्रॉस और म्यूटेशन ऑपरेटरों की परिभाषा भी पूरी तरह से तुच्छ नहीं है, इसलिए ऐसे प्रत्येक कार्य के लिए एक नए एल्गोरिथम का "उत्पादन" विशेष रूप से समय लेने वाला है।
कट के तहत सामग्री अनुकूलन के लिए सबसे प्रसिद्ध आनुवंशिक एल्गोरिदम में से एक का संक्षिप्त विवरण है - अंतर विकास एल्गोरिथ्म (डिफरेंशियल इवोल्यूशन, डीई)।
N चरों के कार्य को अनुकूलित करने की जटिल समस्याओं के लिए, इस एल्गोरिथ्म में इतने अच्छे गुण हैं कि इसे अक्सर पहचान और पैटर्न मान्यता की कई समस्याओं को हल करने के लिए तैयार "बिल्डिंग ब्लॉक" के रूप में माना जा सकता है।
मैं मानूंगा कि पाठक आनुवंशिक एल्गोरिदम के वर्णन में उपयोग की जाने वाली बुनियादी अवधारणाओं से परिचित है, इसलिए मैं तुरंत मामले के सार की ओर मुड़ूंगा, और निष्कर्ष में मैं डी एल्गोरिथ्म के सबसे महत्वपूर्ण गुणों का वर्णन करूंगा।
प्रारंभिक जनसंख्या पीढ़ी
प्रारंभिक जनसंख्या के रूप में,
R R n से
एन वैक्टर का एक यादृच्छिक सेट चुना गया है। प्रारंभिक आबादी के वितरण को हल करने के लिए अनुकूलन समस्या की विशेषताओं के आधार पर चुना जाना चाहिए - आमतौर पर एक नमूना का उपयोग
n- आयामी वर्दी या सामान्य वितरण से दिया जाता है जिसमें गणितीय अपेक्षा और फैलाव होता है।
वंशजों का पुनरुत्पादन
एल्गोरिथ्म के अगले चरण में, प्रारंभिक जनसंख्या के प्रत्येक व्यक्ति
X को
X से अलग यादृच्छिक रूप से चयनित व्यक्ति
C के साथ पार किया
जाता है । वैक्टर
एक्स और
सी के निर्देशांक को आनुवंशिक लक्षण माना जाता है। पार करने से पहले, एक विशेष म्यूटेशन ऑपरेटर का उपयोग किया जाता है - प्रारंभिक नहीं, लेकिन व्यक्तिगत
सी के विकृत आनुवंशिक लक्षण क्रॉसिंग में शामिल हैं:

यहां
ए और
बी को
एक्स और
सी के अलावा अन्य आबादी के यादृच्छिक रूप से चुने गए प्रतिनिधि हैं
। पैरामीटर
एफ तथाकथित को निर्धारित करता है
एक उत्परिवर्तन की ताकत बाहरी शोर द्वारा वेक्टर में शुरू की गई गड़बड़ी का आयाम है। यह ध्यान दिया जाना चाहिए कि एक व्यक्ति
सी के "जीन पूल" को विकृत करने वाला शोर एन्ट्रापी का बाहरी स्रोत नहीं है, लेकिन एक आंतरिक स्रोत - जनसंख्या के यादृच्छिक रूप से चयनित प्रतिनिधियों के बीच का अंतर। नीचे हम इस सुविधा के बारे में अधिक विस्तार से बताएंगे।
क्रॉसिंग इस प्रकार है। संभाव्यता
P को सेट किया जाता है जिसके साथ वंशज
T माता-पिता
C से अगला (उत्परिवर्तन द्वारा उत्परिवर्तित) आनुवांशिक लक्षण प्राप्त करता है
। माता-पिता
एक्स से संबंधित विशेषता संभावना
1 के साथ विरासत
में मिली है
- पी। वास्तव में, गणितीय अपेक्षा
पी के साथ एक द्विआधारी यादृच्छिक चर को
n बार खेला जाता है, और इसकी इकाई मूल्यों के लिए विकृत आनुवंशिक लक्षण माता-पिता
सी (यानी, वेक्टर
सी के संगत समन्वय) से विरासत में मिला (स्थानांतरित) है, और शून्य मानों के लिए, आनुवांशिक विशेषता माता-पिता से विरासत में मिली है।
एक्स नतीजतन, एक वंशज वेक्टर
टी बनता है ।
चयन
एल्गोरिथम के कामकाज के प्रत्येक चरण पर चयन किया जाता है। वंशज वेक्टर
टी के गठन के बाद, उद्देश्य समारोह की तुलना उनके लिए और उनके "प्रत्यक्ष" माता-पिता
एक्स के लिए की जाती है। वैक्टर
एक्स और
टी में से एक को नई आबादी में स्थानांतरित किया जाता है, जिस पर उद्देश्य फ़ंक्शन कम मूल्य पर पहुंचता है (हम कम से कम समस्या के बारे में बात कर रहे हैं)। यहां यह ध्यान दिया जाना चाहिए कि वर्णित चयन नियम एल्गोरिथ्म के संचालन के दौरान आबादी के आकार की अपरिहार्यता की गारंटी देता है।
डे एल्गोरिथ्म की विशेषताओं की चर्चा
सामान्य तौर पर, डीई एल्गोरिथ्म मानक आनुवंशिक एल्गोरिथ्म के संभावित "निरंतर" संशोधनों में से एक है। इसी समय, इस एल्गोरिथ्म में एक महत्वपूर्ण विशेषता है जो बड़े पैमाने पर इसके गुणों को निर्धारित करती है। डे एल्गोरिथ्म में, शोर का स्रोत बाहरी यादृच्छिक संख्या जनरेटर नहीं है, लेकिन एक "आंतरिक" एक है, जिसे वर्तमान आबादी के यादृच्छिक रूप से चयनित वैक्टर के बीच अंतर के रूप में लागू किया गया है। याद रखें कि एक निश्चित सामान्य वितरण से चयनित यादृच्छिक बिंदुओं का एक सेट प्रारंभिक आबादी के रूप में उपयोग किया जाता है। प्रत्येक चरण में, जनसंख्या को कुछ नियमों के अनुसार रूपांतरित किया जाता है, और परिणामस्वरूप, अगले चरण में, यादृच्छिक बिंदुओं का एक सेट फिर से शोर स्रोत के रूप में उपयोग किया जाता है, लेकिन एक नया वितरण कानून इन बिंदुओं से मेल खाता है। प्रयोगों से पता चलता है कि, कुल मिलाकर, जनसंख्या का विकास एक "स्विम ऑफ मिडेज" की गतिशीलता से मेल खाता है (यानी, अंकों का एक यादृच्छिक बादल), जो अनुकूलित विशेषताओं की राहत के साथ-साथ एक पूरे के रूप में आगे बढ़ रहा है, अपनी विशिष्ट विशेषताओं को दोहराता है। खड्ड में गिरने के मामले में, "बादल" इस खड्ड का रूप ले लेता है और बिंदुओं का वितरण ऐसा हो जाता है कि दो यादृच्छिक वैक्टरों के अंतर की गणितीय अपेक्षा को खड्ड के लंबे किनारे के साथ निर्देशित किया जाता है। यह संकीर्ण लम्बी खाइयों के साथ तेजी से गति सुनिश्चित करता है, जबकि समान परिस्थितियों में ढाल विधियों को "दीवार से दीवार तक" कंपन संबंधी गतिशीलता की विशेषता है। दिए गए अनुमानी विचार डी एल्गोरिथ्म की सबसे महत्वपूर्ण और आकर्षक विशेषता को चित्रित करते हैं - उनके लिए "अंतर्निहित" शोर स्रोत के वितरण को समायोजित करने, अनुकूलित फ़ंक्शन के इलाके सुविधाओं को गतिशील रूप से मॉडल करने की क्षमता। यह एल्गोरिथ्म की उल्लेखनीय क्षमता को स्पष्ट रूप से जटिल खड्डों से गुजरने के लिए समझाता है, जो जटिल भूभाग के मामले में भी दक्षता प्रदान करता है।
मापदंडों का चयन
जनसंख्या के आकार
एन के लिए ,
क्यू * एन आमतौर पर अनुशंसित है, जहां
5 <= क्यू <= 10 है ।
उत्परिवर्तन ताकत
एफ के लिए, उचित मान अंतराल से चुने गए हैं
[0.4, 1.0] ,
0.5 एक अच्छा प्रारंभिक मूल्य है, लेकिन समाधान से दूर आबादी के तेजी से अध: पतन के साथ, पैरामीटर
एफ को बढ़ाया जाना चाहिए।
उत्परिवर्तन
पी की संभावना
0.0 से
1.0 तक भिन्न होती है, और किसी को यादृच्छिक खोज द्वारा त्वरित समाधान की संभावना की जांच करने के लिए अपेक्षाकृत बड़े मूल्यों (
0.9 या यहां तक कि
1.0 ) से शुरू होना चाहिए। फिर, पैरामीटर मानों को घटाकर
0.1 या यहां तक कि
0.0 किया जाना चाहिए, जब व्यावहारिक रूप से कोई परिवर्तनशीलता आबादी में पेश नहीं की जाती है और खोज अभिसरण है।
अभिसरण जनसंख्या के आकार और उत्परिवर्तन की ताकत से सबसे अधिक प्रभावित होता है, और उत्परिवर्तन की संभावना ठीक धुन पर कार्य करती है।
संख्यात्मक उदाहरण
जब यह प्रपत्र के मानक रोसेनब्रॉक परीक्षण फ़ंक्शन पर चलाया जाता है, तो डीई विधि की विशेषताएं अच्छी तरह से चित्रित की जाती हैं

इस समारोह में
x = y = 1 पर एक न्यूनतम न्यूनतम है, जो खड़ी दीवारों और एक बहुत सपाट तल के साथ एक लंबे घुमावदार खड्ड के नीचे स्थित है।
जब आप वर्ग में
200 अंकों के समान प्रारंभिक वितरण के साथ शुरू करते हैं
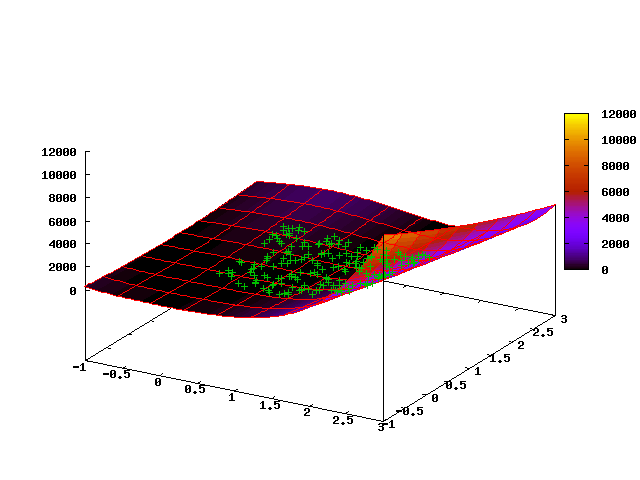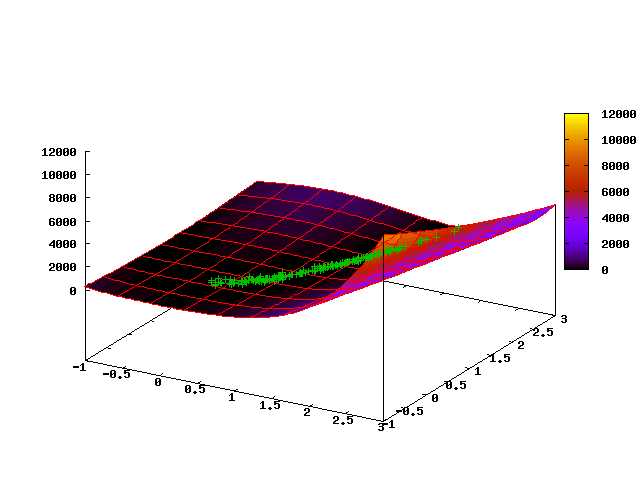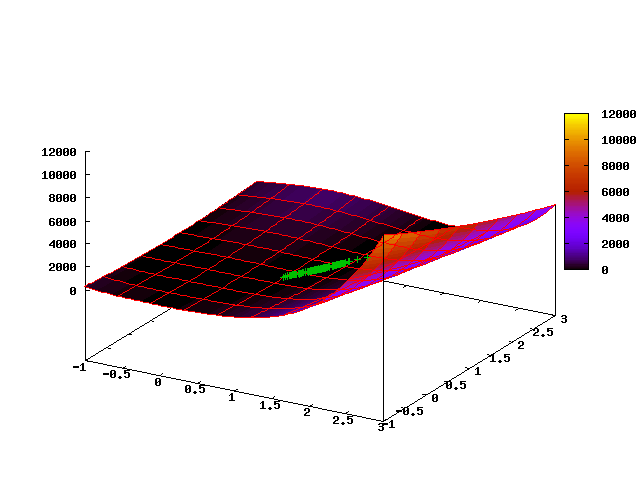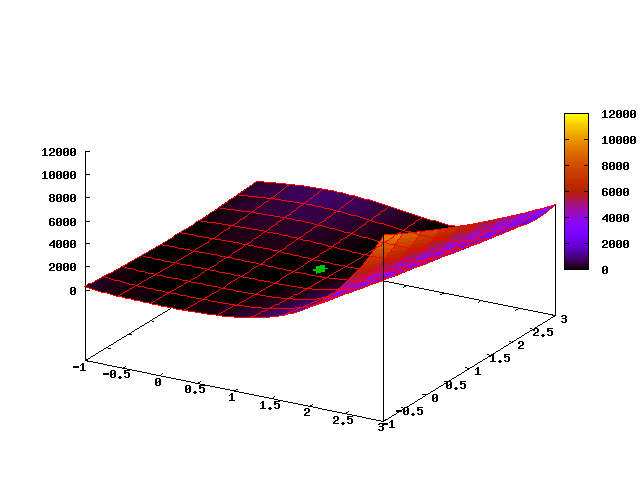
[0, 2] x [0, 2] 15 चरणों के बाद हमें जनसंख्या का निम्नलिखित वितरण मिलता है:

यह देखा जाता है कि "क्लाउड" बिंदुओं को खड्ड के तल के साथ स्थित किया जाता है और अधिकांश उत्परिवर्तनों को खड्ड के नीचे बिंदुओं की एक शिफ्ट की ओर ले जाया जाएगा, अर्थात्। विधि समाधान के स्थान की ज्यामिति की सुविधाओं के लिए अच्छी तरह से अनुकूल है।
निम्नलिखित एनिमेटेड तस्वीर एल्गोरिथ्म के पहले 35 चरणों में एक बिंदु बादल के विकास को दर्शाती है (पहला फ्रेम प्रारंभिक वर्दी वितरण से मेल खाती है):
संदर्भ
- एल्गोरिथ्म के मुख पृष्ठ में विभिन्न क्षेत्रों में कई कार्यान्वयन और उपयोग के उदाहरण हैं।
- लेख में डॉ। डॉब के जर्नल में सी में एक बहुत ही सरल और स्पष्ट कार्यान्वयन शामिल है, जिसे आपकी परियोजनाओं में डी एल्गोरिथ्म का उपयोग करते समय एक आधार के रूप में लिया जा सकता है।