रेटिंग में धोखा के खिलाफ लड़ाई

दूसरे दिन मैंने रेटिंग के बारे में एक दिलचस्प लेख पढ़ा। एक व्यावहारिक मार्गदर्शिका के रूप में, मैं इसका उपयोग करने की अनुशंसा नहीं करता (क्यों इसे टिप्पणियों में देखें), हालांकि, कल्पना दिलचस्प थी और मुझे बहुत सोचा था।
मान लीजिए कि हमारे पास 1 से 5 तक की रेटिंग है। कैसे अनाज को छानने के लिए?


यदि आप एक निश्चित रेटिंग डालने वाले लोगों की संख्या का चार्ट बनाते हैं, तो आप लगभग देख सकते हैं कि कितने वोट घाव थे। बेशक, अन्य आरेखों के साथ तुलना करना आवश्यक है, लेकिन इस तस्वीर से यह स्पष्ट है कि "फाइव्स" का हिस्सा है:



सामान्य तौर पर, एक व्यक्ति आरेख से लपेट को निर्धारित कर सकता है, जिसका अर्थ है कि मशीन भी कर सकती है।

वोटों के वितरण को बीटा वितरण फ़ंक्शन द्वारा वर्णित किया जा सकता है।


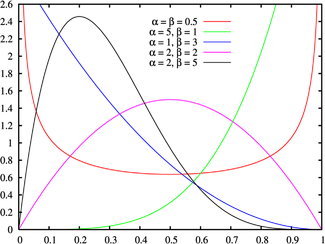
यदि अधिकांश मामलों में मतदान को बीटा फ़ंक्शन द्वारा वर्णित किया जा सकता है, लेकिन भाग में नहीं, तो वोटों का हिस्सा हटाया जा सकता है।


इस प्रकार, हम सभी बुरी आवाज़ों को बाहर नहीं करेंगे, हम कुछ अच्छे लोगों को बाहर करेंगे। कम संख्या में वोट वाले लेखों के लिए, इस तरह के जोड़तोड़ अस्वीकार्य हैं।

बीटा वितरण के दो पैरामीटर हैं, अल्फा और बीटा। हमारे पास दो पैरामीटर भी हैं, औसत स्कोर (ई) और विचरण (डी) - बिखराव का एक उपाय। विकिपीडिया से यह ज्ञात है कि




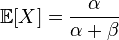
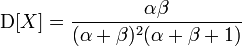
अब हम समीकरणों की प्रणाली को हल करते हैं। यह लंबा और थकाऊ है।

E = a / (a ​​+ b)
d = ab / ((a + b) ^ 2 * (a + b + 1))

E के साथ a / (a ​​+ b) बदलें
d = bE / ((a + b) * (a + b + 1))

1 / (a ​​+ b) को E / a से बदलें
d = b * E ^ 2 / (a ​​* (a + b + 1))

दोनों ओर से गुणा करें (a * (a + b + 1))
d (a * (a + b + 1)) = b * E ^ 2

ब्रैकेट खोलें और स्वैप करें
b * E ^ 2 = दा ^ 2 + दाब + दा

दोनों भागों से थपका घटाव

b * E ^ 2-dab = da ^ 2 + दा

बी (ई ^ 2-डी) = दा (ए + 1)

बी = दा (ए + १) / (ई ^ २-दा)

पहले समीकरण पर वापस

ई = ए / (ए + बी) => (ए + बी) = ए / ई => बी = ए / ई-ए

दोनों समीकरणों को मिलाएं

b = a / E -a = da (a + 1) / (E ^ 2-da)

a / E -a = da (a + 1) / (E ^ 2-da)
एक से विभाजित करें

1 / ई -1 = डी (ए + 1) / (ई ^ 2-डी)

E (E ^ 2-da) से गुणा करें

(1-ई) (ई ^ 2-डी) = एड (ए + 1)

E ^ 2-da -E ^ 3 + Eda = Eda + Ed

एडा सिकुड़ गया

ई ^ 2-दा-ई ^ 3 = एड

E ^ 2 -E ^ 3 -Ed = दा

a = (E ^ 2 -E ^ 3 -Ed) / d

b = a / E -a = a (1 / E-1) = a (१-E) / E = (E ^ 2 -E ^ 3 -Ed) (1-E) / Ed = (E -E ^) 2 -d) (1-E) / d = (E -E ^ 2 -d - E ^ 2 + E ^ 3 + dE / d)

बी = (ई ^ 3-2 ई ^ 2 + ई) / डी + ई -1

नतीजतन, हम एक बीटा फ़ंक्शन का निर्माण कर सकते हैं। सभी रेटिंग इसकी तुलना में अधिक हैं, संभावित मार्कअप। यदि किसी को और अधिक विस्तार से हस्ताक्षर करने में रुचि होगी।