कंप्यूटर पोकर सार

कंप्यूटर पोकर एक बहुत ही गैर-तुच्छ कार्य है, सबसे पहले, क्योंकि खेल राज्यों की बड़ी संख्या है, जो इतनी महान है कि किसी को इस खेल के प्रत्यक्ष समाधान का सपना नहीं देखना पड़ता है। किसी तरह से मशीन को सिखाने का एकमात्र तरीका है कि पोकर कैसे खेलें, उसे अमूर्त में बदलना है - पोकर की एक छोटी सी प्रतिलिपि जिसमें मूल खेल की रणनीतिक स्थितियों को एक साथ जोड़ दिया जाता है। यह पोकर में अमूर्त मुद्दों है कि इस लेख के लिए समर्पित है।

यह प्रकाशन, कुछ हद तक, पहले भाग को संदर्भित करता है और मानता है कि पाठक पोकर के नियमों से परिचित है। मैं प्रस्तुति की लोकप्रिय शैली का पालन करने की कोशिश करूंगा, और विवरणों में रुचि रखने वालों के लिए टिप्पणियों में साहित्य और चर्चा के लिंक हैं।

हमें अमूर्तता की आवश्यकता क्यों है?

कंप्यूटर पोकर की समस्या के पैमाने को भेदने के लिए, मैं सुझाव देता हूं कि आप स्वयं को उस रिपोर्ट [1] से परिचित कराएं, जो सीमा और असीमित पोकर विषयों के आकार को दिखाती है। यहां तक ​​कि "सरलतम" सीमा टेक्सास होल्डम के लिए, वास्तव में 319,365,922,522,608 खेल राज्य हैं जिनमें आपको निर्णय लेने की आवश्यकता है। इसी समय, इस तरह के पोकर में केवल 6378 अलग - अलग गैर-टर्मिनल सट्टेबाजी पैटर्न हैं और गेम स्टेट्स की सारी संपत्ति कार्ड संयोजनों के कारण होती है। असीमित और पॉट-लिमिट विषयों के लिए, ~ 10 ⁶¹ गैर-टर्मिनल इतिहास के आदेश के 500 ब्लाइंड के ढेर के साथ नो-लिमिट होल्डम में - उनकी सीमा से अधिक के लिए शर्त लगाने के दर्जनों आदेश हैं। उपरोक्त पढ़ने के बाद, पाठक को अपने प्रत्यक्ष प्रतिनिधित्व में पोकर को हल करने के लिए आधुनिक कंप्यूटर प्रौद्योगिकी की क्षमता के बारे में संदेह होना चाहिए।

मूल खेल को सरल बनाने के तरीके बचाव के लिए आते हैं, जो इस खेल के रणनीतिक रूप से करीबी राज्यों को एक नए खेल के अप्रभेद्य राज्यों में जोड़ते हैं, जिन्हें अमूर्त कहा जाता है । पोकर के लिए, समस्याओं के दो वर्ग हैं जिन्हें अमूर्तन में ले जाकर हल किया जा सकता है:

• असीमित और पॉट-लिमिट गेम में दांव की समस्या।
• खिलाड़ियों के हाथों का प्रतिनिधित्व करने की समस्या।

एक सार खेल में दांव और उनके प्रतिनिधित्व

पॉट-लिमिट और असीमित पोकर विषयों में दांव की समस्या विशेष रूप से प्रासंगिक है, हालांकि कभी-कभी बड़ी संख्या में खिलाड़ियों के साथ सीमित गेम में सट्टेबाजी के पैटर्न को कम करना पड़ता है। यहां सबसे लोकप्रिय चालों में से एक है दांव का विवेकाधिकार , जब दांव की श्रेणियों को अंतराल में विभाजित किया जाता है और सभी जोड़तोड़ बाद में सीमाओं के साथ बंधे हुए दांव के साथ किए जाते हैं।

असीमित पोकर के लिए विवेकाधीन विकल्प पर विचार करें, जहां दरों को निम्नानुसार परिभाषित किया गया है: बैंक का आधा, पी - बैंक को दर, डी - दोगुना बैंक, एक - सभी में। अन्य सभी दांव उपरोक्त के निकटतम से संबंधित होंगे। पहली नज़र में, दांव की ऐसी अमूर्तता काफी पर्याप्त है और, वास्तव में, इसका उपयोग करने वाले बॉट विरोधियों के साथ खेलने के अच्छे स्तर को प्रदर्शित करते हैं जो एक ही सट्टेबाजी योजना का पालन करते हैं (उदाहरण के लिए, [2])। लेकिन अगर दुश्मन अचानक एक मनमाना दांव लगाता है, असतत एक से बहुत अलग है, तो हमारे लिए बॉट का अपर्याप्त व्यवहार सुनिश्चित किया जाता है। सबसे स्पष्ट संभावित भेद्यता न्यूनतम स्वीकार्य शर्त बनाने वाला एक प्रतिद्वंद्वी है, जिसके बाद बॉट बस मोड़ सकता है। इसके अलावा, असतत सीमाओं के बीच की सीमाएं "overestimated" या "कम करके आंका" फैसलों के बॉट द्वारा गोद लेने की ओर ले जाती हैं, जो एक दूरी पर पैसा खोने और एक व्यक्ति द्वारा बॉट खोलने से भरा है। अधिक असतत श्रेणियों को जोड़ने से स्थिति नहीं बचती है, क्योंकि सार खेल राज्यों की संख्या बढ़ जाती है और कार्ड के सार प्रतिनिधित्व की गुणवत्ता को कम करना पड़ता है।

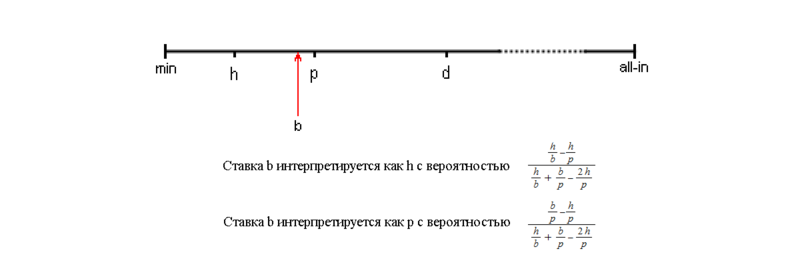एक "हार्ड" प्रसारण के मामले में या एक सार "नरम" एक में और एक सार दरों के मामले में वास्तविक दर बी के लिए अमूर्त दर बी का विवेक।

असली खेल के दांव को अमूर्त में तब्दील करने के लिए ऊपर वर्णित योजना को "कठिन" कहा जाता है। प्रसारण सट्टे का एक और "नरम" तरीका है, जिसका सार यह है कि किसी विशेष अमूर्त के लिए एक वास्तविक शर्त का संबंध यादृच्छिक रूप से निर्धारित किया जाता है, और एक शर्त के लिए वास्तविक दांव के करीब, उच्च सहसंबंध की संभावना अधिक होती है। प्रस्तुति [3] में जानकारी है कि प्रसारण की "नरम" विधि बॉट को दांव के आकार से कम दोहन करने की अनुमति देती है, लेकिन एक ही समय में कम लाभदायक है।

एक पोकर एजेंट का निर्माण करते समय, लोगों के साथ खेलने पर ध्यान केंद्रित किया जाता है, अक्सर वास्तविक गेम वितरणों का विश्लेषण करके दांव का विवेकाधिकार किया जाता है, जिसके बाद प्रत्येक खेल राज्य को अपनी खुद की शर्त विवेकाधीन योजना सौंपी जाती है। हालांकि, यह दृष्टिकोण अमूर्त निर्माण की योजना की पहचान करने के बाद भी कमजोर है। निर्विकारता केवल पोकर दांव का प्रतिनिधित्व करने का एकमात्र तरीका नहीं है। एक दृष्टिकोण भी संभव है, जो इस तथ्य में शामिल है कि पोकर एजेंट बैंक को कड़ाई से परिभाषित मूल्य के अनुरूप लाने के लिए कड़ाई से परिभाषित राशि के लिए बैंक को पूरक करना चाहता है। जाहिर है, ऐसी चाल तुरंत बॉट को उजागर करती है और एक ही समय में गंभीर खामियों के बिना नहीं होती है, उदाहरण के लिए, बैंक के निश्चित आकार से थोड़ा अधिक होने पर, आप बॉट को कार्ड त्यागने के लिए मजबूर कर सकते हैं।

हाल ही में, पोकर में दांव के अमूर्त निर्माण की एक विधि विकसित की गई है, जिसमें एक अन्य गेम एजेंट को पेश किया गया है, जो इस बात पर निर्णय लेता है कि किसी विशेष गेम स्थिति में क्या दांव लगाया जाना चाहिए। [४-५] में, प्रत्येक खेल राज्य में सभी संभावित दांव के बजाय, खिलाड़ियों को केवल तीन बनाने की अनुमति दी जाती है: न्यूनतम शर्त (L), अधिकतम शर्त (H), या सभी में जाना। इस मामले में, एल या एच दोनों में से किस पर दांव लगाने का निर्णय नए गेमिंग एजेंट द्वारा किया जाता है। इस दृष्टिकोण का स्पष्ट लाभ शर्त के साथ बॉट का उपयोग करने में कठिनाई है, लेकिन एक ही समय में एक नए शुरू किए गए एजेंट के प्रशिक्षण के बारे में सवाल उठते हैं, एल और एच दरों के लिए विशिष्ट मूल्य ढूंढते हैं, और एक पूरे के रूप में अमूर्त की प्रस्तुति का आयोजन करते हैं।


असीमित पोकर में दांव पेश करने के विभिन्न तरीके।


कभी-कभी ऐसे सार होते हैं जिनमें ट्रेडिंग सर्कल पर दांव की संख्या सीमित होती है या पिछले सर्कल का इतिहास पूरी तरह से अनुपस्थित है। लेकिन आज, ऐसे दृष्टिकोण विशेष रूप से लोकप्रिय नहीं हैं, क्योंकि वे कमजोर पोकर एजेंट उत्पन्न करते हैं।

अमूर्त में मानचित्र संयोजन

पोकर के लिए एक अमूर्त निर्माण में सबसे कठिन और सबसे महत्वपूर्ण बात कार्ड संयोजनों की प्रस्तुति है। यह वही निर्धारित करता है कि बॉट वर्तमान खेल की स्थिति को पर्याप्त रूप से कैसे महसूस करेगा और रणनीतिक रूप से सही निर्णय लेगा।

नीचे रिपोर्ट [1] से एक तालिका है, जो सट्टेबाजी के प्रत्येक दौर पर टेक्सास होल्डम में सभी प्रकार के कार्ड संयोजनों के आकार को सूचीबद्ध करती है। पहला कॉलम बोर्ड पर कॉमन कार्ड के संयोजन में दोनों खिलाड़ियों को पॉकेट कार्ड वितरित करने के विकल्प प्रस्तुत करता है। दूसरे कॉलम में समान जानकारी है, लेकिन एक खिलाड़ी के लिए, अर्थात जेब कार्ड और सामुदायिक कार्ड के एक जोड़े के संयोजन के लिए। और अंत में, अंतिम कॉलम में एक खिलाड़ी के लिए कार्ड संयोजनों की कोई भी योग्य कक्षाएं नहीं हैं। याद रखें कि समतुल्य संयोजन कार्ड संयोजन के वे सेट हैं जिनमें सूट बदलकर आप उसी सेट से कोई अन्य संयोजन प्राप्त कर सकते हैं। यह स्पष्ट है कि समतुल्य संयोजन में समान रणनीतिक जानकारी होती है।

व्यापार का घेरा	सिर्फ दो खिलाड़ियों के लिए	एक खिलाड़ी के लिए कुल	एकल खिलाड़ी के लिए गैर-समतुल्य
preflop	1,624,350	1,326	169
फ्लॉप	+२८०९४७५७६००	25,989,600	1,286,792
ब्लेकसोर्न	1.264.264.092.000	+१२२१५११२००	55,190,538
नदी	55.627.620.048.000	+५६१८९५१५२००	+२४२८२८७४२०

समतुल्य वर्ग का एक उदाहरण संयोजन के तीसरे दौर पर AKx|TxJy82x का संयोजन है, जहाँ AKx खिलाड़ी के पॉकेट कार्ड हैं, TxJy82x बोर्ड पर कार्ड हैं जो वे दिखाई देते हैं, और x और y ( x!=y , बेशक) चार में से एक ले सकते हैं। सूट के मान {c,s,h,d} । इस प्रकार, वर्ग AKx|TxJy82x में 12 बिल्कुल समान संयोजन होते हैं {AKc|TcJs82c, AKs|TsJc82s, ...} | आइए, AKx|TxJy82x , खिलाड़ी के हाथ में लिखे संयोजन को कॉल करने के लिए सहमत हों, हालांकि यह कुछ हद तक आम तौर पर स्वीकृत परिभाषा के AKx|TxJy82x । फिर भी, शब्द हाथ पूरी तरह से निजी कार्ड की जानकारी की परिभाषा में फिट बैठता है जो केवल एक खिलाड़ी के लिए पूरी तरह से सुलभ है।

हाथों को समकक्ष कक्षाओं में लाने के बाद भी, उनमें से बहुत से प्रत्यक्ष विचार के लिए हैं, इसलिए इन समकक्ष वर्गों को नए, अमूर्त वर्गों में समूहित करना आवश्यक है। बेशक, अब यह प्रक्रिया मूल समकक्ष वर्गों के बारे में जानकारी के कुछ नुकसान के साथ होगी।

हाथों के इस तरह के समूह के उदाहरण के लिए, प्रीफ्लॉप पर विचार करें, क्योंकि उस पर केवल 169 अयोग्य जोड़ी हैं। कई रुचि वाले पाठक प्रसिद्ध सिद्धांतकार और पोकर खिलाड़ी डेविड स्केलांस्की के नाम से परिचित हैं, जिनकी उपलब्धियों में से एक प्रीफ्लॉप खेलने की एक विस्तृत रणनीति है। नीचे दिया गया आंकड़ा स्केलेन्स्की द्वारा प्रस्तावित उनके रणनीतिक मूल्य के अनुसार हाथ शुरू करने के समूहीकरण को दर्शाता है [6]। आठ वर्गों में यह विभाजन केवल एकमात्र सच नहीं है, बल्कि यह पोकर में कार्ड अमूर्त निर्माण के सिद्धांतों के बारे में एक अच्छा विचार देता है।



दुर्भाग्य से, फ्लॉप से ​​शुरू होकर, कार्ड संयोजनों का मैन्युअल विश्लेषण एक बहुत थकाऊ और धन्यवाद रहित कार्य है, इसलिए आपको कक्षाओं में अपने हाथों का विश्लेषण और विभाजन करने के अन्य तरीकों का सहारा लेना होगा। हम कार्ड संयोजनों की संख्यात्मक विशेषताओं के बारे में बात करेंगे, जो चयनित गुणों के अनुसार कार्ड संयोजनों के समूहन की अनुमति देते हैं।

पहले इस्तेमाल की गई विशेषताओं में से एक हाथ की रैंक (हैंड स्ट्रेंथ, HS ) थी, जिसे प्रतिद्वंद्वी के लिए सभी संभव तैयार संयोजनों के अनुपात के रूप में परिभाषित किया गया है, खिलाड़ी के लिए तैयार संयोजन के लिए ताकत में हीन। उदाहरण के लिए, HS(AKx|TxJy82x)=1.0 चूंकि एक तैयार-निर्मित सीनियर फ्लश है, लेकिन HS(AxKy|TzJx82z)~0.43 , जो आश्चर्यजनक नहीं है, क्योंकि z के एक सूट के साथ कार्ड की कोई भी जोड़ी प्रतिद्वंद्वी को फायदा देती है।

HS का विश्लेषण करते समय आपकी आंख को पकड़ने वाली पहली बात यह है कि यह संकेतक इस बारे में कुछ नहीं कहता है कि खिलाड़ी का हाथ बाद के व्यापारिक दौर में कैसे व्यवहार करेगा, इस तथ्य का उल्लेख नहीं करने के लिए कि वितरण इतिहास इस संकेतक के मूल्य को प्रभावित नहीं करता है। लापता जानकारी को भरने के लिए, फ्लॉप से ​​शुरू करके, दो और संकेतक PPot (पॉजिटिव पोटेंशियल) और NPot (नेगेटिव पोटेंशियल) पेश किए जाते हैं। इन PPot संकेतकों में से पहली संभावना यह है कि टेबल पर एक नया कार्ड दिखाई देने के बाद खिलाड़ी के वर्तमान हाथ में सुधार होगा । सुधार का मतलब है कि प्रतिद्वंद्वी के पास नए तैयार किए गए संयोजन नहीं होंगे जो खिलाड़ी के तैयार संयोजन से पुराने हैं। इसी तरह, Npot संभावना है कि एक खिलाड़ी का हाथ मेज पर एक नए कार्ड के साथ खराब हो जाता है। इन संकेतकों और उनकी गणना के लिए प्रक्रियाओं का विस्तृत विवरण [7-8] में पाया जा सकता है। उपरोक्त उदाहरण के लिए, PPot(AKx|TxJy82x)=0 और NPot(AKx|TxJy82x)~0 , जो कि आश्चर्य की बात नहीं है, क्योंकि प्रतिद्वंद्वी को केवल दो जोड़े तैयार होने पर एक पूर्ण घर पर निर्भर रहना पड़ता है। दूसरे मामले के लिए, PPot(AxKy|TzJx82z)~0.15 और NPot(AxKy|TzJx82z)~0.22 और हम देखते हैं कि NPot इस तथ्य के कारण काफी अधिक है कि प्रतिद्वंद्वी फ़्लैश लेने के लिए सूट x के साथ लापता कार्ड को उठा सकता है।

[९] में, जानकारी प्रस्तुत की गई है कि अपेक्षित हैंड रैंक E[HS ^२ ] का वर्ग आपको एक बेहतर अमूर्तता प्रदान करने की अनुमति देता है, क्योंकि यह संकेतक खिलाड़ी के मजबूत हाथों को अधिक लाभ देता है और उन्हें उच्च क्षमता ( PPot ) के साथ हाथों में PPot । यह तर्कसंगत है, क्योंकि हाथों को एक ही रैंक के साथ, लेकिन अलग-अलग क्षमता के साथ, रणनीतिक रूप से अलग-अलग तरीकों से खेला जाना चाहिए।

तीन संकेतक {HS, PPot, NPot} आपको खिलाड़ी के हाथ को अधिक सटीक रूप से चित्रित करने की अनुमति देते हैं, लेकिन उनका एक साथ विचार कुछ असहज हो सकता है, इसलिए, अक्सर प्रभावी हाथ की ताकत ( EHS ) की गणना करने का सहारा लेते हैं, जो दो सूत्रों में से एक द्वारा दिया जाता है [7] -8]: EHS ₁ = HS×(1−NPot)+(1−HS)×PPot , या, EHS ₂ = HS+(1−HS)×PPot । दो सूत्रों के बीच अंतर यह है कि EHS ₂ एक अधिक "आशावादी" पूर्वानुमान देता है, जो एक अधिक आक्रामक खेल को बाहर करने के लिए आवश्यक है।

एक और संकेतक जो कई लोग पहले ही अनुमान लगा चुके हैं कि प्रदर्शन में एक हाथ या अपेक्षित रैंक की संभावना है (शोल्ड हैंड इफेक्ट, E[HS] )। जैसा कि इस विशेषता का नाम स्पष्ट रूप से इंगित करता है, यह उन मामलों के अंश का प्रतिनिधित्व करता है जब वर्तमान खिलाड़ी, प्रदर्शन से पहले खेलना समाप्त कर देता है, प्रतिद्वंद्वी के संभावित संयोजन की तुलना में पुराना संयोजन प्राप्त करता है। इस सूचक का लाभ यह है कि इसमें पहले से ही प्रदर्शन के बाद तक के सभी व्यापारिक हलकों में हाथों की गतिशीलता पर जानकारी शामिल है, NPot और PPot विपरीत, जो केवल एक सड़क की भविष्यवाणी करते हैं। ऊपर दिए गए उदाहरणों में, प्रतिद्वंद्वी के यादृच्छिक हाथ के खिलाफ, इन संकेतकों में निम्नलिखित मान हैं: E[HS](AKx|TxJy82x)~0.99 और E[HS](AxKy|TzJx82z)~0.42 ।

उपरोक्त सभी संकेतकों में कई सामान्य नुकसान हैं। उनमें से पहला, अनुभवी पोकर खिलाड़ियों के लिए सबसे अधिक ध्यान देने योग्य है, यह है कि इन संकेतकों की गणना इस धारणा पर की जाती है कि प्रतिद्वंद्वी का कोई हाथ है। मुद्दा यह है कि पोकर में बहुत कम प्रतिशत हाथ दिखाने के काम आता है, जिसका अर्थ है कि HS , PPot , NPot या E[HS] गणना करते समय हम अपने प्रतिद्वंद्वी को हर संभव पॉकेट कार्ड डालते हैं जो उसके पास कभी नहीं हो सकता है। यह बदले में ऐसे संकेतकों के अनुमानों को अप्रत्याशित रूप से उच्च बनाता है। किसी तरह इस खामी को ठीक करने के लिए, अक्सर हाथों की वेटिंग का उपयोग किया जाता है, जो खेल की स्थिति के आधार पर प्रतिद्वंद्वी के लिए संभव है। विशेष रूप से, एक प्रतिद्वंद्वी को मॉडलिंग करके इस तरह के भार को बाहर किया जा सकता है।

दूसरा दोष यह है कि इन संकेतकों के उपयोग से खिलाड़ी के हाथ के बारे में जानकारी का नुकसान होता है, हालांकि यह इतना स्पष्ट नहीं है। सबसे पहले, यह हाथ की "मेमोरी" की चिंता करता है, अर्थात्, उस क्रम के बारे में जानकारी जिसमें कार्ड बोर्ड पर दिखाई दिया। उदाहरण के लिए, यह स्पष्ट है कि HS(AKx|QJT5x)=HS(AKx|JT5Qx) , जहां पहले मामले में फ्लॉप पर खिलाड़ी पहले से ही तैयार सीधा फ्लश संयोजन था, और दूसरे में - नहीं। इसके अलावा, अक्सर हाथों को अलग-अलग रणनीतिक निर्णयों की आवश्यकता होती है, जो संख्यात्मक संकेतकों के एक-दूसरे मूल्यों के करीब होते हैं, जो मशीन को सिखाने में त्रुटियों का नेतृत्व (और नेतृत्व) कर सकते हैं कि पोकर कैसे खेलें।

अमूर्त संकेतक बनाने के लिए संख्यात्मक संकेतकों के साथ और अधिक जोड़तोड़ इन संकेतकों के कुछ मूल्यों के अनुसार कक्षाओं में हाथों की विभिन्न श्रेणियों को समूहीकृत करने के लिए नीचे आते हैं। उदाहरण के लिए, यदि हम सट्टेबाजी के प्रत्येक दौर में केवल पांच कक्षाएं लेना चाहते हैं, तो हम E[HS] के निम्नलिखित मूल्यों के अनुसार सभी हाथों को समूहित कर सकते हैं:
[0.0–0.2] [0.2–0.4] [0.4–0.6] [0.6–0.8] [0.8–1.0]
अब, एक अमूर्त पोकर गेम को मूल कार्ड संयोजनों के बजाय, हाथों की पाँच श्रेणियों से जोड़ दिया जाएगा। इस तरह के एक अमूर्त खेल को पूरा करने के लिए, व्यापार मंडलियों के परिवर्तन के दौरान कक्षाओं के बीच संक्रमण की संभावनाओं की गणना करना और एक पेआउट मैट्रिक्स को निर्दिष्ट करना भी आवश्यक है जो किसी अन्य के संबंध में हाथों के एक सार वर्ग के "लाभप्रदता" को इंगित करता है।

कक्षाओं में हाथों को समूहित करके एब्स्ट्रक्शन या तो मैन्युअल रूप से या स्वचालित प्रक्रियाओं का उपयोग करके किया जा सकता है, उदाहरण के लिए, डेटा क्लस्टरिंग विधियों का उपयोग करके। अमूर्तता का मैनुअल निर्माण कुछ हद तक बॉट निर्णयों की समझ प्रदान करने, डिबगिंग और रणनीति के समायोजन की सुविधा प्रदान करने की अनुमति देता है, लेकिन यह बहुत समय लेने वाली प्रक्रिया है। स्वचालित समूहीकरण विधियों को अक्सर उन मानदंडों द्वारा निर्देशित किया जाता है जो हमेशा पोकर कार्यों में फिट नहीं होते हैं। दूसरी ओर, स्वचालित दृष्टिकोण आपको आसानी से और जल्दी से अमूर्त के मापदंडों में हेरफेर करने की अनुमति देता है, जो आपको जल्दी और बेहतर ढंग से उपयुक्त कॉन्फ़िगरेशन का चयन करने की अनुमति देता है।

E[HS] मूल्यों के पांच पूर्वनिर्धारित अंतरालों का उपयोग करते हुए कक्षाओं में हाथों को विभाजित करने का उपरोक्त उदाहरण एक दोष है - हाथों को कक्षाओं में असमान रूप से वितरित किया जाता है - केवल कुछ हाथ E[HS] मूल्यों की कुछ सीमा में आते हैं, और बाकी सभी अतिप्रचलित हो जाएंगे। इस स्थिति को ठीक करने के लिए, वे अलग-अलग तरकीबों का उपयोग करते हैं, मैन्युअल रूप से संपादन कक्षाओं से, मात्राओं की गणना करते हुए, नेस्टेड वर्गों, के-साधनों और अन्य में विभाजित करते हैं।


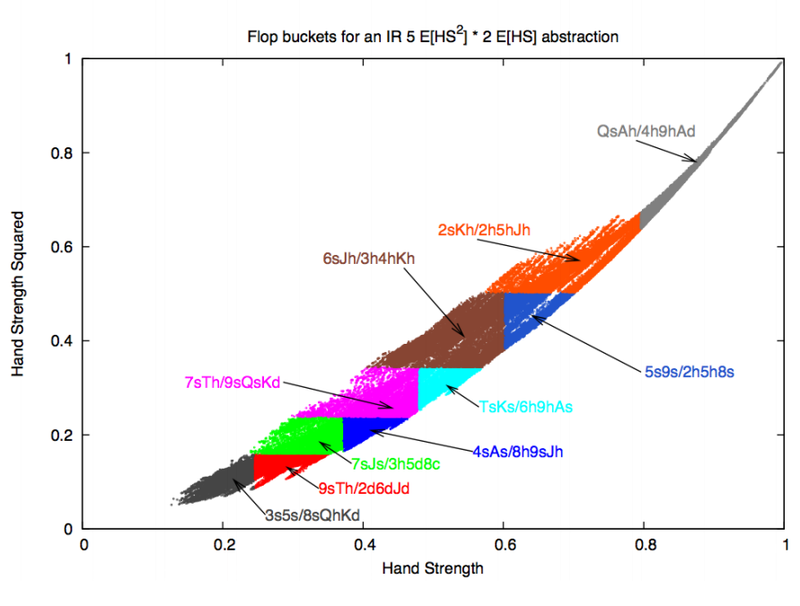नेस्टेड वर्गों में विभाजित फ्लॉप पर संकेतक E[HS ² ] और E[HS] का उपयोग करके हाथों को समूहीकृत करने का एक उदाहरण।

निष्कर्ष

मेरी विनम्र राय में, आधुनिक कंप्यूटर पोकर अमूर्तताओं का एक खेल है, जिसमें एजेंट जिसका अमूर्त बेहतर, अधिक सटीक, और, महत्वपूर्ण रूप से, कम, जीतता है। अमूर्त के आकार को व्यर्थ में उल्लेख नहीं किया गया है, क्योंकि यह उस पर ठीक है कि एजेंट को खेल खेलने के लिए प्रशिक्षण पर खर्च करने का समय निर्भर करता है। और क्या यह सहस्राब्दी, वर्ष, या कुछ घंटों का होगा - यह शोधकर्ता पर निर्भर करता है कि वह अमूर्तन की संरचना को डिजाइन करता है। दुर्भाग्यवश, यह प्रकाशन किसी भी तरह से अमूर्त निर्माण के विभिन्न दृष्टिकोणों का पूरा अवलोकन होने का दावा नहीं कर सकता है, क्योंकि उनमें से बहुत सारे हैं। फिर भी, मुझे लगता है कि इस क्षेत्र में मुख्य बिंदुओं को प्रतिबिंबित किया गया है और कंप्यूटर पोकर की समस्याओं के साथ पाठक को रुचि रखने का लक्ष्य हासिल किया गया है।