रेलवे परिवहन के लिए भौतिक इंजन

नमस्ते
यह लेख रेलवे परिवहन के लिए एक भौतिक इंजन लिखने की अवधारणा प्रस्तुत करता है।
इस भौतिकी इंजन को हल करने वाले मुख्य कार्यों में से एक कारों के बीच बातचीत की गणना करना है।

टकराव का पता लगाना

रेलवे को एक ग्राफ के रूप में दर्शाया जा सकता है, जिसके नोड्स तीर हैं। अनुवाद करते समय, तीर ग्राफ़ के दो आर्क्स को जोड़ता है और तीसरे के साथ कनेक्शन को तोड़ता है। ग्राफ के कई चापों से युक्त वक्र, जिसके साथ कार बिना अनुवाद किए तीर चला सकती है, उसे "मार्ग" कहा जाएगा।
एक ही मार्ग पर कारों के बीच बातचीत एक आयामी स्थान में होती है। अनुवाद के समय, तीरों की गणना की जा सकती है: इस कार के आगे और पीछे कौन सी कार है। जब तक मार्ग पर तीर का अनुवाद नहीं किया जाता है, तब तक कार के कनेक्शन सामने हैं और जो पीछे हैं, अपरिवर्तित रहते हैं।
त्रि-आयामी अंतरिक्ष में, साइड-इफेक्ट चेक रहते हैं जब रास्ते बहुत करीब होते हैं। ऐसे स्थानों पर, विभिन्न मार्गों पर कारें भाग और टकरा नहीं पाएंगी। तीन-आयामी अंतरिक्ष में गणना का अनुकूलन करने के लिए, आप क्षेत्र को कोशिकाओं में विभाजित कर सकते हैं और दिए गए और पड़ोसी कोशिकाओं के भीतर कारों की टक्कर की तलाश कर सकते हैं। इस मामले में, एक ही मार्ग पर कारों के बीच साइड टकराव की जाँच करने की आवश्यकता नहीं है।
उपरोक्त गणना ऑप्टिमाइज़ेशन विधियाँ टकराव खोज एल्गोरिथ्म की जटिलता को लगभग रैखिक रूप से कारों की संख्या पर निर्भर करना संभव बनाती हैं।

एक "मार्ग" पर स्थित कारों की बातचीत की अवधारणा

कार में लगातार आवेग एम.वी.
समय t पर, हम कुल बल वेक्टर F = ma की गणना करते हैं। जो सूत्र के अनुसार इस अवधि के लिए गति P = mv बदलता है:
ए = एफ / एम;
v = (v + a * t);
पी = एम * वी;
कहां: ए - त्वरण, एम - कार द्रव्यमान, वी - कार की गति

अन्य कारों के साथ सहभागिता उनके बीच की गति को स्थानांतरित करके होती है।
कई समस्याओं को हल करने के लिए कारों के बीच इंटरैक्शन एल्गोरिदम को कम किया जाता है।

चुनौती :
समय टी के बाद कारों के निर्देशांक और क्षण की गणना करना आवश्यक है। टी - समय अंतराल एक सेकंड से भी कम।
समाधान :
हम जोड़े में सभी कारों की तुलना करते हैं। कारों के बीच की दूरी एस।
यदि कारों के बीच की दूरी कम हो जाती है (कारें एक-दूसरे की ओर जाती हैं, या एक कार दूसरी कार से पकड़ती है), तो हम गणना करते हैं कि उन्हें टकराने में कितना समय लगता है। हम इस तरह के एक न्यूनतम टकराव समय टी पाते हैं।
यदि एक कार को दूसरे से जोड़ा जाता है, और वे एक दूसरे से दूर जाते हैं, तो हम पाते हैं कि स्वचालित युग्मक को खींचने में कितना समय लगता है। हम स्वचालित युग्मन टी तनाव का न्यूनतम तनाव समय पाते हैं।
हम कारों के बीच न्यूनतम इंटरैक्शन समय पाते हैं: इंटरैक्शन टी = मिनट (टकराव, तनाव) ।
यदि इंटरैक्शन टी> टी है , तो हम कारों को एक समय टी के लिए स्थानांतरित करते हैं और एल्गोरिथ्म को पूरा करते हैं।
अन्यथा, हम टकराने वाली कारों को एक समूह में एकजुट करते हैं, हम उनके लिए एक सामान्य आवेग मानते हैं। इंटरवल के समय को इंटर के t = t- t से घटाएं।
हम सभी कारों को उस दूरी पर ले जाते हैं जो वे इंटरैक्शन टाइम टी के दौरान पास करेंगे।
हम कारों के बीच इंटरैक्शन एल्गोरिदम के संचालन को दोहराते हैं, हम समूह को एक पूरे के रूप में मानते हैं। इसके अलावा, अगर वैगनों का एक समूह दूसरे शरीर से टकराता है, और समूह में एक फैला हुआ स्वचालित युग्मक होता है, तो समूहों को फिर से अलग-अलग वैगनों में विभाजित किया जाना चाहिए, क्योंकि समूह के भीतर वैगन एक साथ करीब आ सकते हैं।

सरलीकरण : चूंकि t एक छोटी सी अवधि है, इसलिए हम मानते हैं कि कार की गति में कुल बल से तुरंत परिवर्तन होता है, जबकि बल अपरिवर्तित रहता है, भले ही कार अपने निर्देशांक को बदल देती है और इसलिए, ट्रैक प्रोफ़ाइल इसके लिए बदल जाती है (झुकाव, ऊंचाई अंतर )। सटीकता बढ़ाने के लिए, हम अंतराल टी को कम समय के अंतराल में विभाजित कर सकते हैं और क्रमिक रूप से एल्गोरिथ्म को कई बार चला सकते हैं।

टास्क: कारों की टक्कर से पहले के समय की गणना।
वैगनों के दो वैगन या समूह होते हैं। उनके बिंदुओं के बीच कुछ दूरी S है जो एक दूसरे के सबसे करीब है

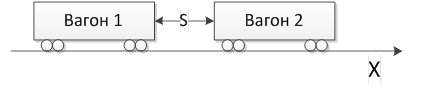
वैगनों का कुछ X समन्वय है। वैगन 2 के X समन्वय का मूल्य वैगन 1 की तुलना में अधिक है। सशर्त रूप से दाईं ओर निर्देशित आंदोलन को सकारात्मक माना जाएगा, बाईं ओर - नकारात्मक।
कम्प्यूटेशनल पुनरावृत्ति की शुरुआत में कार में त्वरण और प्रारंभिक गति होती है। पहली और दूसरी कार के लिए क्रमश: v1 और v2, कारों के त्वरण a2 और a2 द्वारा प्रारंभिक गति को दर्शाया जाएगा।
कारों को टकराने के लिए, उन्हें कुछ समय के लिए दूरी एस को कम करना होगा। समस्या का हल समय टी खोजने के लिए कम हो गया है।
सरलीकरण:
चूंकि कम्प्यूटेशनल सिस्टम की गणना के एक पुनरावृत्ति का समय अंतराल काफी छोटा हो सकता है, हमारा मानना ​​है कि इस अवधि के दौरान कारों को प्रभावित करने वाले ट्रैक प्रोफाइल और अन्य बाहरी कारक बहुत बदल नहीं सकते हैं। इसलिए, गणना के एक पुनरावृत्ति द्वारा त्वरण को स्थिर माना जाएगा।
इसके अलावा, इस एल्गोरिथ्म में घर्षण बल की विशिष्टता को ध्यान में नहीं रखा गया है। आंदोलन के खिलाफ घर्षण बल को निर्देशित किया जाता है। और अगर कार किसी भी बलों के प्रभाव में दिशा बदलती है, तो इस समय त्वरण में काफी बदलाव होना चाहिए, इसलिए घर्षण बल अपनी दिशा बदल देगा और त्वरण पर इसका प्रभाव पड़ेगा।
समाधान:
टक्कर से पहले प्रत्येक गाड़ी चलेगी:
S1 = v1 * t + a1 * t * t / 2 पर पहली कार
S2 = v2 * t + a2 * t * t / 2 पर दूसरी कार
टक्कर से पहले कारों के बीच की प्रारंभिक दूरी पहली और दूसरी कारों के आंदोलन में अंतर है।
एस = एस 1-एस 2;
S = (v1-v2) * t + (a1-a2) * t * t / 2
हमें द्विघात समीकरण मिलता है। इस समीकरण की जड़ समस्या का समाधान होगी।
एल्गोरिथ्म का ब्लॉक आरेख चित्र में दिखाया गया है। C # में इस एल्गोरिदम का कार्यान्वयन लिस्टिंग में दिखाया गया है।

/// <summary> ///        /// </summary> /// <param name="s"> ///         /// 2-   </param> /// <param name="v1">   /</param> /// <param name="v2">   /</param> /// <param name="a1">   /(*)</param> /// <param name="a2">   /(*)</param> /// <returns> ///         . ///            ///      (double.PositiveInfinity) /// </returns> public static double ClashTime(double s, double v1, double v2, double a1, double a2){ double A = (a1 - a2) / 2; double B = v1 - v2; double T; if (Math.Abs(A) < 0.000001) { if (Math.Abs(B) < 0.000001) { T = double.PositiveInfinity; } else { T = s / B; } } else { //   double D = B * B + 4 * A * s; if (D < 0) { T = double.PositiveInfinity; } else { double pD = Math.Sqrt(D) / (2 * A); double pB = -B / (2 * A); double t1 = pB + pD; double t2 = pB - pD; if (t1 >= 0) { if (t2 >= 0) T = Math.Min(t1, t2); else T = t1; } else { if (t2 >= 0) T = t2; else T = double.PositiveInfinity; } } } return T; } 

कार्य: कारों की गति की दिशा को रोकने या बदलने के लिए समय की गणना
एक वैगन या वैगनों का एक समूह एक साथ आगे बढ़ रहा है। कार में एक प्रारंभिक गति वी है। कार पर विभिन्न बल कार्य करते हैं, जो त्वरण A और घर्षण बल देते हैं, जिससे त्वरण Atr मिलता है।
वैगन में कुछ X समन्वय होता है। सशर्त रूप से दाईं ओर जाने पर X निर्देशांक का मान बढ़ता है और बाईं ओर सशर्त रूप से बढ़ने पर घट जाता है। यही है, हम सशर्त रूप से निर्देशित अधिकार को सकारात्मक मानेंगे, और बाईं ओर - नकारात्मक।
आपको यह पता लगाने की आवश्यकता है कि कार को दिशा बदलने या रोकने में कितना समय लगेगा।
सरलीकरण:
चूंकि कम्प्यूटेशनल सिस्टम की गणना के एक पुनरावृत्ति का समय अंतराल काफी छोटा हो सकता है, हमारा मानना ​​है कि इस अवधि के दौरान कारों को प्रभावित करने वाले ट्रैक प्रोफाइल और अन्य बाहरी कारक बहुत बदल नहीं सकते हैं। इसलिए, गणना के एक पुनरावृत्ति द्वारा त्वरण को स्थिर माना जाएगा।
समाधान:
गति की दिशा के खिलाफ घर्षण बल को निर्देशित किया जाता है। इसलिए, इस समस्या को हल करने के लिए, आपको एक समय खोजने की जरूरत है जिस पर गति शून्य हो जाती है।
KofTr - घर्षण बल दिशाओं का संकेत देने वाला गुणांक
ए - घर्षण को छोड़कर सभी बलों के योग के त्वरण का त्वरण
यदि V> 0 तो KofTr = -1 अन्यथा KofTr = 1
V0 + A * T + KofTr * Atr * T = 0
V0 + T * (A + KofTr * Atr) = 0
T = -V0 / (A + KofTr * Atr);

 /// <summary> ///       ///      /// </summary> public static double StoppingTime(double frictionForceAcceleration, double otherForcesAcceleration, double speed) { double Atr = Math.Abs(frictionForceAcceleration); double A = otherForcesAcceleration; double V = speed; double KofTr; if (V == 0) return 0; if (V > 0) KofTr = -1; else KofTr = 1; double a = (A+ KofTr*Atr); // a = 0,    if (Math.Abs(a) < 0. 0000001) return double.PositiveInfinity; // V  a     if (a * V > 0) return double.PositiveInfinity; double t = -V / a; return t; } 

एक कार पर गुरुत्वाकर्षण के प्रभाव की गणना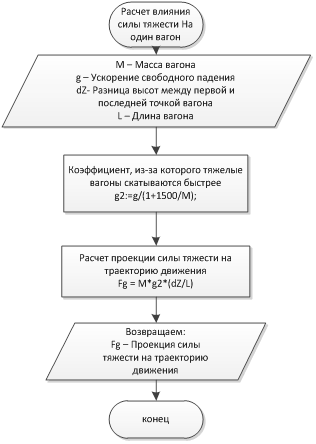


एक कार पर अभिनय करने वाले घर्षण बल की गणना


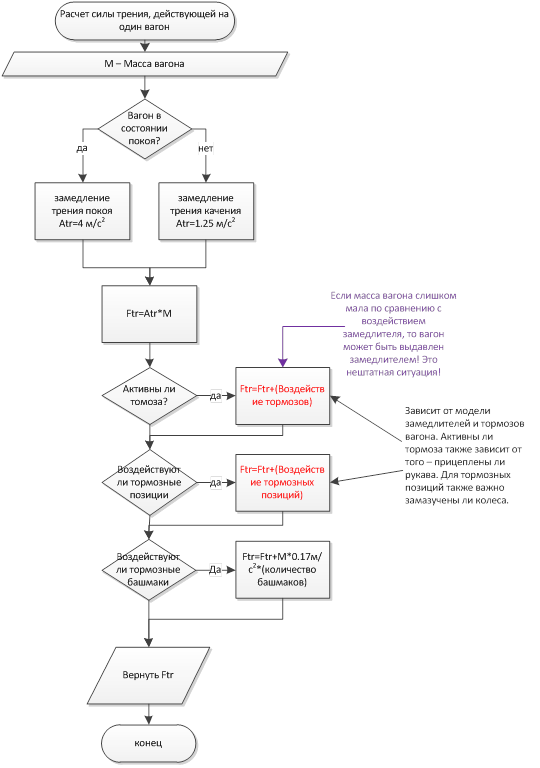वैगन या वैगनों के संबंधित समूह के विस्थापन की गणना


बेशक, यह रेलवे के लिए भौतिक इंजन का सिर्फ एक छोटा सा हिस्सा है, बाकी के बारे में अगले लेख में।