🧝🏾 🕴🏼 🔖 कई चर में बहुपद और हास्केल पर बुचबर्गर एल्गोरिथ्म 🚼 📈 💆

इस लेख में मैं बात करना चाहता हूं कि मैंने हास्केल भाषा में गॉर्नर बेस से संबंधित एल्गोरिदम को कैसे लागू किया। मुझे आशा है कि कोई मेरे विचारों और स्पष्टीकरणों को उपयोगी पाएगा। मैं सिद्धांत में नहीं जा रहा हूं, इसलिए पाठक को एक बहुपद की अंगूठी, एक अंगूठी के आदर्श और एक आदर्श के आधार की अवधारणाओं से परिचित होना चाहिए। मैं आपको आईसीएमएमओ की इस पुस्तक को पढ़ने की सलाह देता हूं, इसमें सभी आवश्यक सिद्धांत का विस्तार से वर्णन किया गया है।

लेख का मुख्य विषय कई चरों के बहुपद छल्लों के आदर्शों का गॉर्नर बेस है। बहुपद समीकरणों की प्रणालियों का अध्ययन करते समय यह अवधारणा उत्पन्न होती है। लेख के अंत में, मैं उदाहरण के द्वारा प्रदर्शित करूंगा कि इन विचारों को कैसे लागू किया जा सकता है।

इस सिद्धांत का सबसे महत्वपूर्ण परिणाम कई चर में समीकरणों के बहुपद प्रणालियों को हल करने का एक अच्छा तरीका है। यहां तक कि अगर आप उच्च बीजगणित या हास्केल के साथ परिचित नहीं हैं, तो मैं आपको इस लेख को पढ़ने की सलाह देता हूं, क्योंकि इन समान समाधान विधियों को छात्र के लिए सुलभ स्तर पर समझाया गया है, और पूरे सिद्धांत को सही ठहराने की जरूरत है। आप उच्च बीजगणित से संबंधित सभी चीजों को सुरक्षित रूप से छोड़ सकते हैं, और समीकरणों के सिस्टम को हल करना सीख सकते हैं।

यदि आप रुचि रखते हैं, तो कृपया, बिल्ली के नीचे।

मैं चित्रों के लिए माफी माँगता हूँ - यह लेटेक्स द्वारा प्रस्तुत किया गया है, लेकिन कैसे समझ style="width:...;height=...;" बनाने के लिए style="width:...;height=...;" मुझे नहीं पता यदि आप मुझे एक बेहतर तरीका बताते हैं, तो मैं निश्चित रूप से इसे फिर से करूँगा।

1 बीजगणित से सबसे आवश्यक अवधारणाएं

जिन तत्वों के सेट पर आप दो ऑपरेशन निर्दिष्ट कर सकते हैं - "जोड़" और "गुणन", नियमों के एक निश्चित सेट (स्वयंसिद्ध) के अनुरूप, बीजगणित में छल्ले कहलाते हैं। कई चरों में बहुपद जिनके गुणांक वास्तविक संख्याएं हैं, जिनके द्वारा निरूपित एक वलय होता है

, बहुपद के अलावा और गुणा के साधारण स्कूल संचालन के सापेक्ष। एक अंगूठी का एक आदर्श इसका एक सबसेट है, जिसमें से दो तत्वों का अंतर निहित है, और इसके किसी भी तत्व का उत्पाद और अंगूठी का एक मनमाना तत्व इस सबसेट में निहित है। एक आदर्श का सबसे सरल उदाहरण पूर्णांक की अंगूठी में एक आदर्श के रूप में कई पांच नंबरों का सेट है। सुनिश्चित करें कि यह आदर्श है। अगर यह काम करता, तो आगे कोई समस्या नहीं होती।

इसके अलावा हम बहुपद रिंग में केवल आदर्शों पर विचार करेंगे। बहुपत्नी के कुछ परिमित सेट

आदर्श का आधार कहा जाता है यदि आदर्श से किसी बहुपद का प्रतिनिधित्व किया जा सकता है

जहाँ

- कुछ बहुपद। इस तथ्य को निम्नानुसार लिखा गया है:

। हिल्बर्ट का आधार प्रमेय एक उल्लेखनीय परिणाम देता है - किसी भी आदर्श (एक बहुपद में) का एक सीमित आधार होता है। यह आपको किसी भी स्थिति में काम करने की अनुमति देता है, बस आदर्शों के परिमित ठिकानों के साथ काम करता है।

अब हम निम्नलिखित फॉर्म के समीकरणों की प्रणालियों पर विचार करेंगे:

हम इस प्रणाली के आदर्श को आदर्श कहते हैं

। यह बीजगणित से ज्ञात है कि कोई भी बहुपद आदर्श रूप से झूठ बोल रहा है

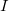
मूल प्रणाली के किसी भी समाधान पर गायब हो जाता है। और आगे, अगर

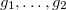
- आदर्श का एक और आधार

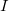
तब प्रणाली

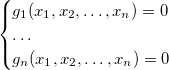
मूल एक के रूप में एक ही समाधान है। इस सब से यह इस प्रकार है कि यदि हम सिस्टम के आदर्श को खोजने का प्रबंधन करते हैं जो मूल से सरल है, तो सिस्टम को स्वयं हल करने का कार्य सरल है।

जादुई रूप से, ऐसा आधार मौजूद है - इसे आदर्श का ग्रोब्नेर आधार कहा जाता है। परिभाषा के अनुसार, यह ऐसा आधार है कि आदर्श से किसी भी बहुपद के लिए शेष (लगभग बाद में) के साथ विभाजन प्रक्रिया एक शून्य शेष है। यदि हम इसका निर्माण करते हैं, तो इसका एक बहुपद, कम से कम ज्यादातर मामलों में, केवल एक चर पर निर्भर करेगा, जो हमें अनुक्रमिक प्रतिस्थापन द्वारा संपूर्ण प्रणाली को हल करने की अनुमति देगा।

आखिरी चीज जो हमें चाहिए

बहुपद और कसौटी

Buchberger युगल। हम मोनोमियल ऑर्डर करने के कुछ "अच्छे" तरीके चुनते हैं (विवरण के लिए, पुस्तक देखें) और द्वारा निरूपित करें

बहुपत्नी के वरिष्ठ शब्द (इस आदेश के सापेक्ष)

और के माध्यम से

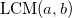
- मोनोमियल के सबसे छोटे सामान्य कई

और

। तो

-पॉलिनोमियल से

और

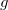
निम्नलिखित निर्माण को कहा जाता है:

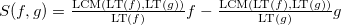
सिद्ध (कसौटी)

-पेयर) कि एक आदर्श का आधार उसका गॉब्नेर आधार है यदि और केवल यदि

- इसके सदस्यों में से किसी भी जोड़ी से एक बहुपद एक शेष 0 देता है जब एक आधार से विभाजित किया जाता है (जैसा कि यह नीचे समझाया जाएगा)। यह तुरंत इस तरह के आधार के निर्माण के लिए एल्गोरिथ्म का संकेत देता है:

आधार बहुपद की प्रत्येक जोड़ी के लिए, उनकी रचना करें -पॉलिमोनियल और इसे शेष के आधार पर विभाजित करें।
यदि सभी अवशेष शून्य के बराबर हैं, तो गॉबनेर आधार प्राप्त होता है। अन्यथा, सभी नॉनज़ेरो अवशिष्टों को आधार से जोड़ें और चरण 1 पर लौटें।

यह बुचबर्गर एल्गोरिथ्म है - इस लेख का मुख्य विषय। यह सब गणित के साथ है, आप आगे बढ़ सकते हैं। यदि आपको कुछ समझ में नहीं आता है, तो आपको विकिपीडिया या एक किताब को देखना चाहिए, हालांकि आगे के कथन में उच्च बीजगणित के ज्ञान की आवश्यकता नहीं है।

2 हास्केल में कई चर से बहुपद का प्रतिनिधित्व

हम मोनोमियल से बहुपद का प्रतिनिधित्व करना शुरू करते हैं। एक मोनोमियल केवल दो चीजों की विशेषता है - एक गुणांक और चर की डिग्री का एक सेट। हम मानते हैं कि चर हैं

।

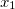
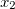
और इसी तरह। फिर मोनोमियल

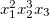
1 और डिग्री का गुणांक है [2,3,1] , और [2,3,1]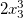

- गुणांक 2 और डिग्री [0,0,3] । शून्य डिग्री पर ध्यान दें! वे अन्य सभी तरीकों के कार्यान्वयन के लिए महत्वपूर्ण हैं। सामान्य तौर पर, हमें आवश्यकता होती है कि सभी मोनोमियल (एक समस्या के ढांचे के भीतर) की डिग्री की सूचियों की लंबाई समान हो। यह हमारे काम को बहुत सरल करेगा।

हमें "मोनोमियल" प्रकार का वर्णन बीजगणितीय डेटा प्रकार के गुणांक (प्रकार " c ") और डिग्री की सूची (प्रत्येक प्रकार " a ") के रूप में करते हैं:

 data Monom ca = M c [a] deriving (Eq)

हमें एक दूसरे के साथ मोनोमियल की तुलना करने की आवश्यकता होगी, इसलिए यह Ord क्लास के एक अवतार को लिखने का समय है। मैं सामान्य लेक्सिकोग्राफिक आदेशों का उपयोग डिग्री द्वारा करूँगा, क्योंकि यह बहुत सरल है और एक ही समय में मोनोमियल के "अच्छे" ऑर्डर के नियमों का अनुपालन करता है। हम केवल अपने सिस्टम के साथ काम करने की सुविधा के लिए Show क्लास का अवतार भी लिखेंगे।

 instance (Eq c, Ord a) => Ord (Monom ca) where compare (M _ asl) (M _ asr) = compare asl asr instance (Show a, Show c, Num a, Num c, Eq a, Eq c) => Show (Monom ca) where show (M c as) = (if c == 1 then "" else show c) ++ (intercalate "*" $ map showOne $ (filter (\(p,_) -> p /= 0) $ zip as [1..])) where showOne (p,i) = "x" ++ (show i) ++ (if p == 1 then "" else "^" ++ (show p))

show फ़ंक्शन स्मार्ट होने की कोशिश करता है: यह गुणांक नहीं दिखाता है यदि यह 1 है, और यह डिग्री शून्य के चर नहीं दिखाता है, और न ही यह चर की पहली डिग्री दिखाता है। इस तरह:

 *Main> M 2 [0,1] 2x2 *Main> M 1 [2,2] x1^2*x2^2

मैं show समय show लिए समान कार्य लिखूंगा, इसलिए यह यह समझने के लायक है कि यह कैसे काम करता है - मुझे यकीन है कि यह निश्चित रूप से किसी को डराता है। zip as [1..] का उपयोग करते हुए zip as [1..] प्रत्येक डिग्री को उसके चर की संख्या के साथ गोंद करते हैं, फिर

filter (
(p _) -> p /= 0)

साथ

filter (
(p _) -> p /= 0)

filter (
(p _) -> p /= 0)

filter (
(p _) -> p /= 0)

शून्य डिग्री से छुटकारा पा

filter (
(p _) -> p /= 0)

हैं, प्रत्येक चर के विवरण को showOne माध्यम से एक स्ट्रिंग में बदल showOne और अंत में सब कुछ एक साथ गोंद कर देते हैं, गुणन चिह्न के साथ Data.List करते हुए, Data.List से Data.List का उपयोग करते हैं।

अब हम वास्तविक प्रकार के बहुपद का वर्णन करने के लिए तैयार हैं। इसके लिए, एक नियमित सूची पर एक नया newtype रैपर उपयुक्त है:

 newtype Polynom ca = P [Monom ca] deriving (Eq) instance (Show a, Show c, Num a, Num c, Eq a, Eq c) => Show (Polynom ca) where show (P ms) = intercalate " + " $ map show ms

इस बार, show फ़ंक्शन सरल है, क्योंकि सभी गंदे काम पहले से ही मोनोमियल के प्रकार में छिपे हुए हैं। यह इस तरह काम करता है:

 *Main> P [M 1 [3,1], M 1 [2,2], M 1 [1,1]] x1^3*x2 + x1^2*x2^2 + x1*x2

हम भविष्य के लिए सहमत हैं कि इस सूची में मोनोमियल हमेशा अवरोही क्रम में संग्रहीत किया जाएगा ( Ord के अवतार की हमारी परिभाषा के अर्थ में)। इससे कुछ चीजों को लागू करना आसान हो जाएगा।

बहुपद पर 3 ऑपरेशन

सबसे सरल ऑपरेशन एलटी हैं, शून्य के लिए समानता के लिए परीक्षण और एक संख्या से गुणा। मोनोमियल के ऑर्डर पर हमारे समझौते से यह इस प्रकार है कि सबसे बड़ा मोनोमियल हमेशा सूची में पहले स्थान पर आता है और इसे head का उपयोग करके प्राप्त किया जा सकता है। एक मोनोमियल को शून्य माना जाता है यदि इसका गुणांक शून्य है, और एक बहुपद यदि इसमें मोनोमियल नहीं है। ठीक है, एक स्थिरांक से गुणा करना गुणांक को बदलता है:

 lt :: Polynom ca -> Monom ca lt (P as) = head as zero :: (Num c, Eq c) => Monom ca -> Bool zero (M c _) = c == 0 zeroP :: Polynom ca -> Bool zeroP (P as) = null as scale :: (Num c) => c -> Monom ca -> Monom ca scale c' (M c as) = M (c*c') as

दो मोनोमियल को समान कहा जाएगा यदि वे केवल गुणांक द्वारा भिन्न होते हैं। उनके लिए, राशि निर्धारित की जाती है - आपको बस गुणांक जोड़ने की आवश्यकता है, और डिग्री को अपरिवर्तित छोड़ दें।

 similar :: (Eq a) => Monom ca -> Monom ca -> Bool similar (M _ asl) (M _ asr) = asl == asr addSimilar :: (Num c) => Monom ca -> Monom ca -> Monom ca addSimilar (M cl as) (M cr _) = M (cl+cr) as

दो मोनोमियल को गुणा करने के लिए, हम बस प्रत्येक चर की डिग्री जोड़ते हैं। इस ऑपरेशन को महान zipWith फ़ंक्शन के साथ लागू करना बहुत आसान है। मुझे लगता है कि कोड खुद के लिए बोलता है:

 mulMono :: (Num a, Num c) => Monom ca -> Monom ca -> Monom ca mulMono (M cl asl) (M cr asr) = M (cl*cr) (zipWith (+) asl asr)

बहुत अधिक रोचक बहुपद का जोड़ है। हम इस समस्या को पुनरावर्ती रूप से हल करेंगे। तुच्छ मामले - दो शून्य बहुपद (खाली सूची) का योग शून्य बहुपद के बराबर है। किसी भी बहुपद और शून्य का योग इसके बराबर होता है। अब हम दोनों बहुपदों को नॉनजेरो मान सकते हैं, जिसका अर्थ है कि उनमें से प्रत्येक को वरिष्ठ शब्द और बाकी हिस्सों में विभाजित किया जा सकता है - "पूंछ"। दो मामले हैं:

वरिष्ठ सदस्य समान हैं। इस स्थिति में, उन्हें जोड़ दें और पूंछ के योग में परिणाम जोड़ें (यदि यह नॉनज़ेरो है)।
वरिष्ठ सदस्य समान नहीं हैं। फिर बड़ा वाला चुनें। हमारी आदेश देने की स्थिति यह गारंटी देती है कि दोनों बहुपदों की पूंछ में एक समान मोनोमियल नहीं है। इसलिए, हम चयनित बहुपद की पूंछ को दूसरे के साथ मोड़ सकते हैं, और फिर इस सबसे बड़े मोनोमियल को इसकी शुरुआत में जोड़ सकते हैं।

यह ध्यान देने योग्य है कि इस पुनरावर्ती प्रक्रिया के परिणामस्वरूप, हम फिर से एक आदेशित बहुपद प्राप्त करते हैं, और स्वयं कोड लिखते हैं।

 addPoly :: (Eq a, Eq c, Num c, Ord a) => Polynom ca -> Polynom ca -> Polynom ca addPoly (P l) (P r) = P $ go lr where go [] [] = [] go as [] = as go [] bs = bs go (a:as) (b:bs) = if similar ab then if (zero $ addSimilar ab) then go as bs else (addSimilar ab):(go as bs) else if a > b then a:(go as (b:bs)) else b:(go (a:as) bs)

बहुपद का गुणन पूरी तरह से प्राकृतिक तरीके से प्राप्त किया जाता है। बहुपद द्वारा एक mulMono को गुणा करना बहुत सरल है - बस इसे map और mulMono का उपयोग करके प्रत्येक mulMono द्वारा गुणा map । और फिर हम दो बहुपद के उत्पाद में वितरण ("वितरण कानून", कोष्ठक के प्रकटीकरण) को लागू करते हैं और हम पाते हैं कि हमें केवल पहले बहुपद के सभी मोनोमियल को दूसरे से गुणा करना होगा और परिणाम जोड़ना होगा। हम एक ही map का उपयोग करके गुणा करेंगे, और परिणाम का उपयोग करके foldl' और addPoly । इन दोनों ऑपरेशनों के लिए कोड आश्चर्यजनक रूप से कम है - टाइप विवरणों की तुलना में कम!

 mulPM :: (Ord a, Eq c, Num a, Num c) => Polynom ca -> Monom ca -> Polynom ca mulPM (P as) m = P $ map (mulMono m) as mulM :: (Eq c, Num c, Num a, Ord a) => Polynom ca -> Polynom ca -> Polynom ca mulM l@(P ml) r@(P mr) = foldl' addPoly (P []) $ map (mulPM r) ml

यह सब है, हमने बहुपदों पर बुनियादी क्रियाओं को लागू किया, जिसका अर्थ है कि हम आगे बढ़ सकते हैं!

आधार पर शेष के साथ 4 विभाजन (कमी)

हम कहते हैं कि मोनोमियल

मोनोमियल द्वारा विभाजित

अगर इस तरह के एक मोनोमियल मौजूद है

कि

। जाहिर है, यह केवल तभी सच है जब प्रत्येक चर में शामिल किया गया हो

से कम नहीं

। इसलिए, पहले से ही परिचित zipWith फ़ंक्शन और अद्भुत and फ़ंक्शन का उपयोग करके विभाज्यता जांच को लागू किया जा सकता है। और सत्यापन के साथ, वास्तविक विभाजन प्रक्रिया प्राप्त करना आसान है:

 dividable :: (Ord a) => Monom ca -> Monom ca -> Bool dividable (M _ al) (M _ ar) = and $ zipWith (>=) al ar divideM :: (Fractional c, Num a) => Monom ca -> Monom ca -> Monom ca divideM (M cl al) (M cr ar) = M (cl/cr) (zipWith (-) al ar)

ध्यान दें कि अब गुणांक प्रकार को विभाजन की अनुमति देना चाहिए - Fractional वर्ग। यह निराशाजनक है, लेकिन कुछ भी नहीं किया जा सकता है।
एक शेष के साथ एक बहुपद को एक आधार में विभाजित करने के लिए एल्गोरिथ्म अनिवार्य रूप से एक स्तंभ द्वारा एक साधारण विद्यालय विभाजन है। आधार के बहुपद के बीच, पहले बहुपद को इस तरह चुना जाता है कि लाभांश के वरिष्ठ शब्द को उसके वरिष्ठ शब्द से विभाजित किया जाता है, फिर इस बहुपद को उनके वरिष्ठ सदस्यों के भागफल से गुणा किया जाता है। घटाव का परिणाम एक नए लाभांश के रूप में लिया जाता है और प्रक्रिया को दोहराया जाता है। यदि आधार के किसी भी वरिष्ठ सदस्य द्वारा वरिष्ठ सदस्य को विभाजित नहीं किया जाता है, तो विभाजन पूरा हो जाता है और अंतिम लाभांश को शेष कहा जाता है।

हमारी मुख्य विभाजन प्रक्रिया, चलो इसे reduceMany कहते हैं, दो सहायक की आवश्यकता होगी - reducable और reduce । उनमें से पहला जाँचता है कि क्या बहुपद एक दूसरे से विभाज्य है, और दूसरा विभाजन करता है।

 reducable :: (Ord a) => Polynom ca -> Polynom ca -> Bool reducable lr = dividable (lt l) (lt r) reduce :: (Eq c, Fractional c, Num a, Ord a) => Polynom ca -> Polynom ca -> Polynom ca reduce lr = addPoly lr' where r' = mulPM r (scale (-1) q) q = divideM (lt l) (lt r)

चूंकि हमारे पास घटाने के लिए कोई फ़ंक्शन नहीं है, बस दूसरे बहुपद को -1 से गुणा करें और उन्हें जोड़ें - यह सरल है! और यहाँ पूरे विभाजन एल्गोरिथ्म है:

 reduceMany :: (Eq c, Fractional c, Num a, Ord a) => Polynom ca -> [Polynom ca] -> Polynom ca reduceMany h fs = if reduced then reduceMany h' fs else h' where (h', reduced) = reduceStep h fs False reduceStep h (f:fs) r | zeroP h = (h, r) | otherwise = if reducable hf then (reduce hf, True) else reduceStep h fs r reduceStep h [] r = (h, r)

कम reduceMany फ़ंक्शन एक आधार में एक बहुपद को विभाजित करने का प्रयास करता है। यदि विभाजन हुआ, तो प्रक्रिया जारी रहती है, अन्यथा यह समाप्त हो जाती है। आंतरिक फ़ंक्शन reduceStep करना reduceStep सिर्फ पहले बहुपद के लिए दिखता है जिसे विभाजित किया जा सकता है, और विभाजित होता है, शेष और एक ध्वज को दर्शाता है कि क्या विभाजन हुआ है।

5 बुचबर्गर एल्गोरिथम

तो हम इस लेख के मुख्य भाग पर आते हैं - बुचबर्गर एल्गोरिदम का कार्यान्वयन। हमारे पास अभी तक केवल एक ही चीज़ नहीं है

-polynomial। इसका कार्यान्वयन बहुत सरल है, साथ ही साथ कम से कम बहुविध मोनोमियल खोजने के लिए एक सहायक कार्य है:

 lcmM :: (Num c, Ord a) => Monom ca -> Monom ca -> Monom ca lcmM (M cl al) (M cr ar) = M (cl*cr) (zipWith max al ar) makeSPoly :: (Eq c, Fractional c, Num a, Ord a) => Polynom ca -> Polynom ca -> Polynom ca makeSPoly lr = addPoly l' r' where l' = mulPM l ra r' = mulPM r la lcm = lcmM (lt l) (lt r) ra = divideM lcm (lt l) la = scale (-1) $ divideM lcm (lt r)

यहां, दोनों बहुपदों को केवल इसी मोनोमियल द्वारा गुणा किया जाता है, इसके अलावा दूसरा भी शून्य से एक होता है, जैसा कि शेष के साथ विभाजन के मामले में होता है।
मुझे यकीन है कि इस एल्गोरिथ्म को लागू करने के कई तरीके हैं। मैं यह भी ढोंग नहीं करता हूं कि मेरा कार्यान्वयन इष्टतम या सरल है। लेकिन मुझे यह पसंद है और यह काम करता है, और यह सब लेता है।

मेरे द्वारा उपयोग किए जाने वाले दृष्टिकोण को गतिशील कहा जा सकता है। हमारे आधार को दो भागों में विभाजित करें - वह जिसमें हमने पहले ही जाँच कर ली है (और जोड़ दी गई है)

- सभी जोड़े से बहुपद - " checked " - और यह केवल ऐसा करने के लिए आवश्यक है - " add "। एल्गोरिथ्म का एक कदम इस तरह दिखेगा:

पहले बहुपद को दूसरे भाग से लें
लगातार निर्माण करें इसके पहले भाग के सभी बहुपद और दूसरे भाग के अंत में सभी गैर-अक्षीय अवशेषों को जोड़ दें
इस बहुपद को पहले भाग में ले जाएँ

जैसे ही दूसरा भाग खाली होगा, पहले में गॉबनेर आधार होगा। इस तरह के समाधान का लाभ यह है कि उन्हें नहीं माना जाएगा

-पॉलिमोनिअल्स उन जोड़ियों से जिनमें से उन्हें पहले से ही गिना और जांचा जाता है। इस प्रक्रिया में महत्वपूर्ण कार्य checkOne । यह एक बहुपद (दूसरे भाग से), साथ ही दोनों हिस्सों को लेता है, और बहुपद की एक सूची देता है जिसे आधार में जोड़ा जाना चाहिए। हम पहले भाग में साधारण पुनरावर्तन का उपयोग करते हैं, स्वाभाविक रूप से शून्य अवशेषों को जोड़े बिना:

 checkOne :: (Eq c, Fractional c, Num a, Ord a) => Polynom ca -> [Polynom ca] -> [Polynom ca] -> [Polynom ca] checkOne f checked@(c:cs) add = if zeroP s then checkOne f cs add else s:(checkOne f cs (add ++ [s])) where s = reduceMany (makeSPoly fc) (checked++add) checkOne _ [] _ = []

निश्चित रूप से इसे एक foldl द्वारा बदला जा सकता है, लेकिन मैं इसे एक अभ्यास के रूप में छोड़ दूंगा। यह केवल इस आधार पर Gröbner आधार का निर्माण करने के लिए बनी हुई है। एल्गोरिथ्म स्टेप वर्बटीम का कार्यान्वयन इसके विवरण को दोहराता है, अपने लिए देखें:

 build checked add@(a:as) = build (checked ++ [a]) (as ++ (checkOne a checked add)) build checked [] = checked

बहुपद पहले भाग में चला जाता है, और इसके सभी गैर-अवशेष अवशेष दूसरे में आते हैं। कृपया ध्यान दें कि यह वास्तव में जांचने के लिए पर्याप्त है

भागों के बीच बहुपद के आंदोलनों के कारण केवल पहले के साथ दूसरे भाग के प्रत्येक बहुपद का बहुवचन। यह नोट करना बाकी है कि इस से ग्रोबनेर आधार प्राप्त करने के लिए, यह पहले भाग में अपने बहुपद में से एक को डालने के लिए पर्याप्त है, दूसरे में बाकी है और build प्रक्रिया को लागू करता है, जो makeGroebner फ़ंक्शन में किया जाता है।

 makeGroebner :: (Eq c, Fractional c, Num a, Ord a) => [Polynom ca] -> [Polynom ca] makeGroebner (b:bs) = build [b] bs where build checked add@(a:as) = build (checked ++ [a]) (as ++ (checkOne a checked add)) build checked [] = checked

6 उपयोग के उदाहरण

इन तरीकों के व्यावहारिक अनुप्रयोग का प्रदर्शन किए बिना ये सभी सैद्धांतिक निर्माण पूरी तरह से बेकार लगते हैं। एक उदाहरण के रूप में, तीन सर्कल के चौराहे बिंदु को खोजने की समस्या पर विचार करें - एक नक्शे पर स्थिति का सबसे सरल मामला। हम समीकरणों की प्रणाली के रूप में हलकों के समीकरण लिखते हैं:

।

कोष्ठक खोलने के बाद, हमें निम्नलिखित मिलते हैं:

आइए Gröbner आधार का निर्माण करें (मैंने अधिक सटीकता के लिए Rational प्रकार का उपयोग किया):

 *Main> let f1 = P [M 1 [2,0], M (-2) [1,0], M 1 [0,2], M (-26) [0,1], M 70 [0,0]] :: Polynom Rational Int *Main> let f2 = P [M 1 [2,0], M (-22) [1,0], M 1 [0,2], M (-16) [0,1], M 160 [0,0]] :: Polynom Rational Int *Main> let f3 = P [M 1 [2,0], M (-20) [1,0], M 1 [0,2], M (-2) [0,1], M 76 [0,0]] :: Polynom Rational Int *Main> putStr $ unlines $ map show $ makeGroebner [f1,f2,f3] x1^2 + (-2) % 1x1 + x2^2 + (-26) % 1x2 + 70 % 1 x1^2 + (-22) % 1x1 + x2^2 + (-16) % 1x2 + 160 % 1 x1^2 + (-20) % 1x1 + x2^2 + (-2) % 1x2 + 76 % 1 (-20) % 1x1 + 10 % 1x2 + 90 % 1 15 % 1x2 + (-75) % 1

चमत्कारिक रूप से, हमें दो रैखिक समीकरण मिले जो जल्दी से एक उत्तर देते हैं - बिंदु (7.5)। आप यह सत्यापित कर सकते हैं कि यह तीनों सर्किलों पर है। तो, हमने तीन जटिल द्विघात समीकरणों की प्रणाली के समाधान को दो सरल रैखिक लोगों के लिए कम कर दिया है। Gröbner कुर्सियां इस तरह के कार्यों के लिए एक बहुत उपयोगी उपकरण हैं।

प्रतिबिंब और निष्कर्ष के लिए 7 प्रश्न

वास्तव में, इस परिणाम में अभी भी सुधार किया जा सकता है।

-पॉलिनॉमिअल्स को केवल उन बहुपद के जोड़े के लिए विचार करने की आवश्यकता है जिनके वरिष्ठ सदस्य मैथुन नहीं कर रहे हैं - अर्थात, उनकी सबसे छोटी बहु केवल उनका उत्पाद नहीं है। इस मामले के बारे में कुछ सूत्रों का कहना है कि "बहुपद एक लिंक है "। इस अनुकूलन को हमारे makeGroebner फ़ंक्शन में जोड़ें।

यदि एक बहुपद जिसका वरिष्ठ शब्द आधार से कुछ अन्य बहुपद के वरिष्ठ शब्द से विभाजित होता है, अंतिम आधार में आता है, तो इसे बाहर रखा जा सकता है। इस तरह के सभी बहुपद के बहिष्करण के बाद प्राप्त आधार को न्यूनतम ग्रोनेर आधार कहा जाता है। आप एक बहुपद पर भी विचार कर सकते हैं जिसका मनमाना शब्द किसी अन्य बहुपद के वरिष्ठ शब्द से विभाजित है। इस मामले में, इस बहुपद को दूसरे के विभाजन से शेष के साथ बदलें। जिस प्रकार से इस प्रकार के सभी संभावित ऑपरेशन किए जाते हैं उसे कम कहा जाता है । एक अभ्यास के रूप में, न्यूनतमकरण और आधार की कमी को लागू करें।

अंत में, मैं उन सभी को धन्यवाद देना चाहता हूं जिन्होंने इस लेख को अंत तक पढ़ा है। मुझे पता है कि मेरी कहानी कुछ गड़बड़ थी, और कोड अपूर्ण था (और शायद समझ से बाहर), लेकिन मुझे अभी भी उम्मीद है कि मुझे गॉर्नर के ठिकानों में किसी की दिलचस्पी है। मुझे बहुत खुशी होगी अगर कोई मेरी उपलब्धियों के लिए कम से कम कुछ वास्तविक कार्यों में आवेदन पा सकता है।

लेख से सभी कोड gist के रूप में उपलब्ध है।

कई चर में बहुपद और हास्केल पर बुचबर्गर एल्गोरिथ्म