दूसरे दिन, वायु प्रवाह दर को मापने के लिए एक उपकरण को प्रोग्राम करने का कार्य था। एक मापने वाले तत्व के रूप में - सेंसर स्पष्ट नहीं है कि कौन सा निर्माता है, कोई विशेषता या कोई पर्याप्त पैरामीटर नहीं हैं। कोई विकल्प नहीं था, अंशांकन विशेषताओं को हटाने और स्थानांतरण फ़ंक्शन "एडीसी-स्ट्रीम रीडिंग" को प्रदर्शित करना आवश्यक था।
चूंकि सेंसर, लगभग किसी भी मापने वाले उपकरण की तरह, तापमान के प्रति बहुत संवेदनशील है, मुझे विभिन्न तापमानों के लिए विशेषताओं (न्यूनतम 3) के एक परिवार को निकालने की आवश्यकता थी।
डेटा को विभिन्न तरीकों से MathCad में दर्ज किया जा सकता है, मैंने इसे ट्रांसपोज़्ड रो वैक्टर के रूप में करना पसंद किया:

इसके बाद, "मजबूत-इच्छाशक्ति" निर्णय द्वारा अनुमानित फ़ंक्शन के प्रकार को सेट करना और प्रत्येक अंशांकन विशेषता को अनुमानित करना आवश्यक है। इसलिए, मेरी विशेषताओं को लिनफिट फ़ंक्शन का उपयोग करते हुए, एक तृतीय-डिग्री बहुपद द्वारा सफलतापूर्वक अनुमानित किया जाता है, जो कि मनमाने कार्यों के रैखिक संयोजनों के रूप में एक समाधान की तलाश में है, मुझे तीन बहुपद के लिए गुणांक मिला:

यह देखने के लिए कि परिणामी बहुपद द्वारा "सफल" प्रयोगात्मक डेटा कैसे बनाए जाते हैं, आप एक ग्राफ बना सकते हैं:

अब, तापमान सुधार शुरू करने के लिए, किसी को तापमान पर प्रत्येक बहुपद गुणांक की निर्भरता खोजने की आवश्यकता है, अर्थात। केवल बाधाओं के लिए उपरोक्त करें। प्रयोगात्मक डेटा अब गुणांक और तापमान मान स्वयं होंगे। मैं वास्तव में चाहता था कि तापमान निर्भरता रैखिक थी, लिनफिट फ़ंक्शन का उपयोग अनावश्यक रूप से रैखिक सन्निकटन के लिए करना संभव है, लेकिन:

अंत में, निम्न रूप में वांछित निर्भरता दिखाई देती है:
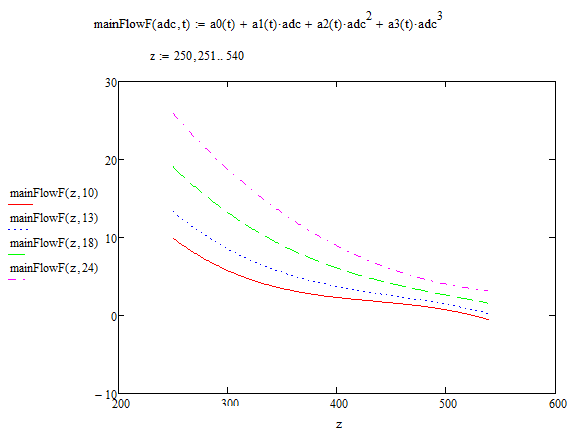
परिणाम पर टिप्पणी करते हुए, मैं ध्यान देता हूं कि यह बहुत अच्छी तरह से काम नहीं करता था, स्पष्ट रूप से घृणित। विशेषताओं को शुरू में खराब तरीके से शूट किया गया था, एक सामान्य स्टैंड की कमी ने प्रभावित किया। और सामान्य तौर पर, अंशांकन कार्य शौकिया तौर पर दूर है, आपने इसे घुटने पर नहीं किया है। लेकिन मैं दृष्टिकोण के बारे में बात करना चाहता था।