पहला भागदूसरे भाग का पहला भागदूसरे भाग का दूसरा भागखैर, सज्जनों, यह खत्म करने का समय है। चक्र के अंतिम लेख में (जिसका शीर्षक मेरे टेम्पलेट को तोड़ता है जो वास्तव में अभी तक जाग नहीं हुआ है), हम इस कार्य के इतिहास में एक बुलेट डालेंगे। इस तथ्य के बावजूद कि दूसरे भाग की टिप्पणियों में ऐसा करने के लिए एक अधिक सुविधाजनक और सार्वभौमिक तरीका सुझाया गया था, मैं अभी भी उन उपकरणों का उपयोग करूंगा जो मैंने व्यक्तिगत रूप से लेखों के पहले लिखने से पहले विकसित किए थे। सबसे पहले, अच्छाई को खोना नहीं है, और दूसरी बात, मुझे लगता है कि हर कोई समझता है कि कार्य केवल सुंदर चित्र खींचने के लिए एक बहाना है और उन्हें हब में पोस्ट करना है। खैर, जैसा कि वे कहते हैं, यह शुरू हुआ।
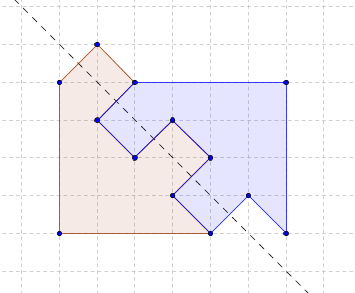
केस 3: मूविंग सिमिट्री
स्लाइडिंग समरूपता निम्नलिखित मापदंडों द्वारा निर्धारित की जाती है: समरूपता की धुरी और इसके समानांतर कतरनी वेक्टर। समरूपता का अक्ष, बदले में, विमान पर दिशा और विशिष्ट स्थिति से निर्धारित होता है। अब मैं एक-दूसरे से कई तथ्यों को रेखांकित करूंगा, स्पष्ट रूप से पर्याप्त उन्हें नींबू भी नहीं कहना चाहिए, और साबित करने के लिए भी कम।
- चलती समरूपता की धुरी सीमाओं से समान है (हम समानांतर हस्तांतरण के मामले से सीमा के गैर-चुनिंदा रूप से अवधारणा लेते हैं)।
- यदि हम अलग-अलग सीमाओं पर एक खंड को समाप्त करते हैं, तो सममिति का अक्ष इसके मध्य से होकर गुजरेगा।
- चलती समरूपता के अक्ष की दिशा निर्धारित करने के बाद, हम स्वचालित रूप से इसकी विशिष्ट स्थिति को पहचानते हैं। यदि दोनों सीमाओं में एक ही बिंदु होता है, तो हम शिफ्ट वेक्टर को भी जानते हैं।
- जिन हिस्सों में आकृति को अक्ष द्वारा विभाजित किया गया है, उनका क्षेत्रफल बराबर है (यह तथ्य पिछले वाले से अनुसरण नहीं करता है)
इन तथ्यों के साथ, मैंने यह चित्र खींचा है:

यह देखा जा सकता है कि सीमाओं पर अधिकांश दिशाओं के लिए या तो अंक ए और ई होंगे, या बिंदु बी और एफ होंगे, और इसलिए, अक्ष आंकड़ा के "केंद्र" (आयत ओबीएफ के विकर्ण के चौराहे) के माध्यम से जाएगा। प्रचलन में दूसरे स्थान पर अंक सी और एफ के साथ मामले का कब्जा है, माननीय तीसरा - अंक सी और ए के साथ। इन मामलों में, जाहिर है, समरूपता की धुरी क्रमशः सीएफ और सीए के मध्य बिंदुओं से होकर गुजरेगी।
अब देखते हैं कि अक्ष को किन दिशाओं में दो समान भागों में विभाजित किया जाएगा। थकाऊ विवरण के बिना, मैं बस इतना ही कहूंगा: लेकिन इस तरह के साथ।
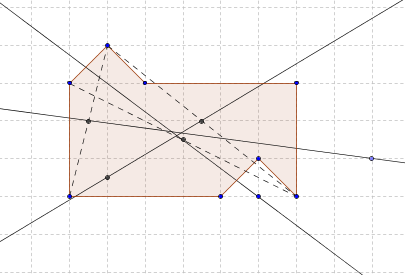
अब हमारे पास तीन विशिष्ट कुल्हाड़ी हैं और, इसके अलावा, तीन विशिष्ट शिफ्ट वैक्टर उनके साथ जुड़े हुए हैं - क्योंकि सभी मामलों में सीमाएं एक बिंदु से मिलकर होती हैं। यह दिखाना आसान है कि इन तीनों चलती समरूपताओं के लिए उस आकृति के बिंदु हैं जिनके लिए न तो एक छवि है और न ही एक उलटा छवि है - जो, लेम्मा 3 के अनुसार, इसका मतलब है कि ये खराब, बेकार चलती समरूपताएं हैं जो आकृति को दो समान भागों में विभाजित करने के अनुरूप नहीं हो सकती हैं। मैं पाठक के लिए विशिष्ट बिंदुओं की खोज को छोड़ता हूं।
निष्कर्ष
चित्र A
0 को दो समान भागों में
नहीं काटा
जा सकता है । अब मैं संशोधित करने के लिए स्पष्ट विवेक के साथ जाऊंगा "और यहां के लोग शांत हैं।" हैप्पी विजय दिवस, खब्रोवित्स को याद दिलाता है।