ऑफ़लाइन और ऑनलाइन 2GIS उत्पादों में एकल रूटिंग का निर्माण

अगर किसी और को नहीं पता है, तो 2 जीआईएस शहर के नक्शे के साथ संगठनों की एक मुफ्त निर्देशिका है। और अगर निर्देशिका के बारे में पहले से ही बहुत कुछ लिखा गया है , तो मानचित्र और इसकी क्षमताओं के बारे में कम जानकारी है। और कुछ बताना है। उदाहरण के लिए, रूटिंग के बारे में - हमने मौजूदा समाधान क्यों नहीं लिया, लेकिन हमने खुद लिखा है या हमें विभिन्न उत्पादों में एकीकृत निर्माण एल्गोरिदम की आवश्यकता क्यों है।




2012 की शुरुआत में, हमें पहली बार एक समस्या का सामना करना पड़ा - जो इंजन पहले डेस्कटॉप संस्करण में उपयोग किया गया था, वह संसाधनों पर बहुत अधिक मांग कर रहा है और इसका उपयोग मोबाइल उपकरणों पर नहीं किया जा सकता है । कुछ करना जरूरी था।

तैयार समाधान क्यों नहीं बनाते हैं?

एक राय है कि रूटिंग इंजन कार्यान्वयन की सूक्ष्मताओं के एक समूह के साथ एक असंभव कार्य है। यह ऐसा है जैसे कि आप को बढ़ावा नहीं मिलता है :: ग्राफ़ और आपको इसे नहीं लेना चाहिए (जिसके लिए फिल्म शूट नहीं की गई है, यह पता नहीं है, हाँ) और इसके लिए तैयार समाधान खोजना आसान है। शायद, लेकिन हमारे मामले में नहीं।

मुझे उम्मीद है कि यह लेख से स्पष्ट हो जाएगा - सामान्य ज्ञान, थोड़ा सा रोमांच और हर चीज के लिए तैयार गाइड किसी भी समस्या को हल कर सकता है।

निष्पक्षता में, यह ध्यान दिया जाना चाहिए कि मुझे पहले से ही ग्राफ़ में खोज के साथ काम करने का अनुभव था (~ 50 मिलियन कोने), इसलिए इस तरह की समस्याओं को हल करने के बारे में पहले से ही कुछ विचार थे।

तो परिचय:

1. सर्वर संस्करण में, एक ही कोड काम करना चाहिए, लेकिन विभिन्न सेटिंग्स के साथ;
2. पथ का निर्माण उचित समय में सेल फोन पर काम करना चाहिए;
3. संपत्ति में एक तैयार (और सत्यापित) रोड ग्राफ है; यह तैयार किए गए समाधानों को खोजने और तेज करने की तुलना में बहुत आसान / अधिक सुविधाजनक / सस्ता निकला।

बुनियादी (और, सामान्य रूप से, केल) सिद्धांतों को नकारें :

1. भंडारण संरचनाएं सरल होनी चाहिए।
2. लिंक की स्थानीयता को प्रोत्साहित करना उपयोगी है, अर्थात। यदि डेटा ग्राफ़ के भौतिक रूप से करीब (उदाहरण के लिए) कोने को संदर्भित करता है, तो डिस्क पर उन्हें संभव होने पर पास में स्थित होना चाहिए।
3. किसी भी स्थिति में डिस्क पर मौजूद ग्राफ तत्वों को एक बार में एक्सेस नहीं किया जाना चाहिए; रीडिंग केवल बैचों में की जाती है।
4. निम्न-स्तरीय कैशिंग कम उपयोग की है, आपको केवल "महंगी" वस्तुओं का ध्यान रखना चाहिए। उदाहरण के लिए, सीधे कैशिंग डिस्क कॉल के बजाय, उनकी संख्या को कम से कम एल्गोरिदमिक रूप से ध्यान रखना बेहतर है।
5. ग्राफ़ में खोज लॉजिक को जहाँ संभव हो, सरलीकृत किया जाना चाहिए, क्योंकि "यदि पाइप लाइन टूट जाती है" (C)
6. डिस्क पर डेटा संपीड़ित करना अच्छा है।
7. प्रदर्शन के पक्ष में सटीकता की उपेक्षा निंदनीय नहीं है।

मुख्य विचार

1. जाली पर कोने के निर्देशांक लगाएं। यानी फ़्लोटिंग पॉइंट निर्देशांक को पूर्णांक में अनुवाद करें। जाली को रफ बनाया जा सकता है, इसके स्टेप को बढ़ाते हुए जब तक कि वर्टिस एक साथ चिपकना शुरू न करें या इससे भी बदतर हो, शून्य लंबाई के किनारों के किनारे। जब हमें खोज रहे हैं, तो अंतिम (और डिबगिंग) तक शेष दूरी का अनुमान लगाने के लिए निर्देशांक की आवश्यकता होगी और जब ग्रिड बड़ी वृद्धि में हो, तो फिनिश लाइन के पास, एल्गोरिदम अजीब तरीके से व्यवहार करना शुरू कर देगा।
   ध्यान दें कि झंझरी, मोटे डिस्क पर डेटा की छोटी मात्रा होगी, इसलिए यदि आप वास्तव में चाहते हैं, तो इसे पुनरावृत्त रूप से चुना जा सकता है। हमारे पास एक मीटर की ग्रिड पिच है।
   
   
   
   यह ग्रिड पर लगाए गए ग्राफ़ का एक टुकड़ा जैसा दिखता है।
2. हम मानसिक रूप से अपने ग्राफ की सीमा को एक आयताकार टाइलों की एक संख्या में विभाजित करते हैं जो एक जाली का निर्माण करती है। इस जाली को चोटियों पर एक उदात्तीकरण नहीं होना चाहिए।
3. एक टाइल एक तार्किक इकाई है जो डिस्क और कैशिंग से एक साथ लोड होने के अधीन है। इसमें सभी कोने और आउटगोइंग आर्क शामिल हैं (यानी ऐसे आर्क हैं जिनका प्रारंभिक कोने इस टाइल में स्थित हैं)। प्लस संबंधित जानकारी, यदि कोई हो।
   
   
   
   मास्को के रोड ग्राफ के एक टुकड़े के उदाहरण से किनारों का एक टाइल में गिरना।
4. टाइल का आकार ग्राफ के आकार के आधार पर चुना जाना चाहिए। चूंकि हम डिस्क से कुछ लोड कर रहे हैं, यह डिस्क बफर के आकार के साथ पढ़ने के लिए कुल जानकारी के लिए उचित होगा। एक सौ बाइट्स फिट करने वाली कई चोटियों तक पहुंचने के लिए डिस्क एक्सेस के रूप में भारी तोपखाने का उपयोग करना अजीब होगा। बेशक, ग्राफ समान रूप से व्यवस्थित नहीं है, लेकिन आप औसत मूल्यों के लिए अपील कर सकते हैं, उदाहरण के लिए, ग्राफ डिस्क पर 20mb लेता है, अर्थात। 2500 8K पृष्ठ, इसलिए ग्राफ की सीमा को 50 × 50 भागों (sqrt (2500)) में देखना। यहाँ यह माना जाता है कि टाइल के बारे में सभी जानकारी एक ही स्थान पर है। यदि यह मामला नहीं है, तो एक उचित संशोधन किया जाना चाहिए।
5. यह टाइल्स को कैश करने के लिए समझ में आता है।
6. मेमोरी में लोड किया गया ग्राफ (या इसका एक हिस्सा) बड़ी संख्या में छोटी वस्तुएं हैं। बड़ी मात्रा में छोटी वस्तुओं को अलग-थलग नहीं किया जा सकता है और उन्हें नपुंसक बना दिया जाता है। इसलिए, हम जहां भी संभव हो, सत्र-आधारित पृष्ठ आवंटनकर्ताओं का उपयोग करेंगे। गति और काफी कम स्मृति विखंडन के अलावा, यह डेटा ब्लॉक के प्रस्तावना और उपसंहार (अर्थात डबल-लेबल एल्गोरिदम) पर भी बचाएगा।
   पृष्ठ आबंटक मेमोरी से संबंधित निश्चित आकार के पृष्ठों (यदि संभव हो) से वितरित करता है, जिसे वह सिस्टम से आवश्यकतानुसार पूछता है। केवल सभी स्मृति को उसके विध्वंसक में तुरंत मुक्त कर दिया जाता है।
7. एक टाइल में आवश्यक रूप से ऐसा एलोकेटर होगा, जो कुछ भी लोड होने पर बाहर खड़ा होगा, उससे लिया जाएगा और कैश से मजबूर होने पर इसकी टाइल से मर जाएगा।
8. पृष्ठ आवंटनकर्ता का उपयोग करने के लिए एक अन्य उम्मीदवार वास्तविक खोज है, इस तरह से ग्राफ के पारित हिस्से के बारे में जानकारी संग्रहीत करना सुविधाजनक है
9. दरअसल सर्च एल्गोरिथ्म। हम साधारण A * का प्रयोग, एकल "तरंग" में, यात्रा की गई दूरी (या समय) के योग के रूप में और शेष के एक अनुमान के रूप में शीर्ष मान के साथ करेंगे।
10. क * - क्योंकि यह आपको मूल दिक्क्स्ट्रा एल्गोरिथम की तुलना में ट्रैवर्स की गई चोटियों की संख्या को कम करने की अनुमति देता है।
11. एक लहर में - दो कारणों से। सबसे पहले, एक दूसरे की ओर दो तरंगों का प्रक्षेपण, हालांकि यह ग्राफ के ट्रैवर्स किए गए हिस्से को कम कर देगा, जब से रोक मापदंड को जटिल करेगा अगर दो लहरें टकराती हैं तो हमें लगातार जांच करनी चाहिए। और यह या तो ट्रैवर्सेड चोटियों के एक गतिशील सेट की प्रत्येक लहर की सामग्री, या सीधे भरी हुई टाइलों के संशोधन की आवश्यकता है।
12. दूसरा कारण - आने वाली लहर की उपस्थिति आपको गतिशील रूप से पसलियों की लागत को प्रभावित करने की अनुमति नहीं देगी, उदाहरण के लिए, जब तक हम मानसिक रूप से इस पसलियों को प्राप्त करते हैं, तब तक यातायात की स्थिति में बदलाव के कारण।
13. शेष पथ की लागत का एक अनुमान कोई भी हो सकता है, बशर्ते कि त्रिकोण असमानता का उल्लंघन न हो। उदाहरण के लिए, आप एक ईमानदार यूक्लिडियन दूरी या चेबीशेव दूरी का उपयोग कर सकते हैं।

स्रोत डेटा

1. ग्राफ के कार्यक्षेत्र - निर्देशांक और पहचानकर्ता वाली संरचनाएं
2. किनारों में प्रारंभ और अंत कोने की पहचानकर्ता, लंबाई, प्रकार और पहचानकर्ता होते हैं। सभी पसलियां अप्रत्यक्ष हैं।
3. सीमाएं - किनारों की जोड़ी, जिनके बीच संक्रमण असंभव है। बाधा दोनों किनारों के लिए एक विशिष्ट शीर्ष से जुड़ी है। हम प्रतिबंधों के इस तरह के बल्कि छंटे हुए संस्करण का वर्णन करते हैं; यदि आवश्यक हो, तो पाठक आसानी से एक सामान्यीकरण के साथ आएंगे।

पूर्व उपचार

1. ग्राफ की समावेशी सीमा का पता लगाएं।
2. एक समन्वित ग्रिड के साथ निर्धारित।
3. टाइल्स के ग्रिड पर निर्णय लें। प्रत्येक टाइल को अपना पहचानकर्ता सौंपा गया है। पहचानकर्ता एक संख्या है जो कुछ व्यापक वक्र के परिणामस्वरूप बढ़ता है। इस तरह के एक वक्र एक क्षैतिज स्कैन (इग्लू), एक हिल्बर्ट वक्र या थोड़ा इंटरलेविंग वक्र (zorder) हो सकता है। द्वारा और बड़े, केवल उस बिंदु को निर्धारित करने में सक्षम होना महत्वपूर्ण है जिसमें यह बिंदु के निर्देशांक में किस टाइल में गिरता है। और व्यापक वक्र का विकल्प केवल डेटा को संपीड़ित करने की क्षमता को प्रभावित करता है।
4. हम प्रत्येक शीर्ष को एक विशिष्ट टाइल पर असाइन करते हैं। उसी समय, हम प्रत्येक शीर्ष को इसकी टाइल में इसके क्रमांक संख्या को असाइन करते हैं, यह संपीड़न के लिए भी उपयोगी है।
5. प्रत्येक किनारे के लिए, हम यह निर्धारित करते हैं कि यह किस टाइल से आता है और कौन सा इसे प्राप्त करता है, साथ ही आउटगोइंग और इनकमिंग पॉइंट्स की आंतरिक संख्या भी।

डिस्क भंडारण

डेटा स्वयं बी-पेड़ों में संग्रहीत किया जाता है, इसकी एक किस्में में अधिक सटीक रूप से।
डेटा वेयरहाउस से, हमें छांटे गए एन-ओके सरणी को स्टोर करने की क्षमता चाहिए और जल्दी से उनके अंतराल को पढ़ना चाहिए।

द्वारा और बड़े पैमाने पर, भंडारण की पसंद मौलिक नहीं है, हमने बी-पेड़ चुने, क्योंकि वे:

1. समझने और डिबग करने में आसान
2. विशिष्टताओं से बंधे बिना डेटा को संपीड़ित करने देता है
3. सबसे महत्वपूर्ण बात, उनके कार्यान्वयन को हाथ से परीक्षण किया गया था।

तो कई पेड़ हैं:

1. चोटियों का पेड़। इस पेड़ के N-ka में 4 तत्व होते हैं:

• वर्टेक्स टाइल आईडी
• इस टाइल में शीर्ष क्रम संख्या
• X - बिंदु समन्वय
• Y बिंदु का समन्वय है।

2. पसलियों का पेड़ , उनकी कुंजी में 7 तत्व होते हैं:

• आउटबाउंड टाइल आईडी
• इसकी टाइल में निवर्तमान शीर्ष संख्या
• वर्टेक्स टाइल आईडी
• इसकी टाइल में आने वाले शीर्ष की संख्या
• रिब लागत, जैसे लंबाई
• एज प्रकार, जैसे सड़क वर्ग
• किनारे का बाहरी पहचानकर्ता।

3. पहचान करने वालों का पेड़। बाहरी दुनिया के साथ संवाद करने के लिए कार्य करता है। कुंजी में 5 तत्व शामिल हैं:

• बाहरी बढ़त पहचानकर्ता
• आउटबाउंड टाइल नंबर
• इसकी टाइल में निवर्तमान शीर्ष संख्या
• भीतर का टाइल नंबर
• इसकी टाइल में आने वाले शीर्ष की संख्या।

4. लंबाई 4 की कुंजी के साथ प्रतिबंध पेड़:

• बाधा शीर्ष की टाइल संख्या।
• टाइल में इस शीर्ष की संख्या
• किनारे की बाहरी पहचानकर्ता जहां से आंदोलन निषिद्ध है
• किनारे की बाहरी पहचानकर्ता जहां आंदोलन निषिद्ध है।

एक विचारशील पाठक कहेगा: “बाह! एक टाइल के बारे में सभी जानकारी को पढ़ने के लिए, आपको पेड़ों पर 3 लाइनें करने की आवश्यकता है। क्या एक BLOB में सब कुछ पैक करना और इसे गिराना एक झपट्टा मारना बेहतर नहीं है? ”केवल-पढ़ने के लिए डेटा के लिए, यह बेहतर है, ज़ाहिर है, गति और संपीड़न गुणवत्ता दोनों में। लेकिन यह अतिरिक्त काम, अतिरिक्त परीक्षण है। इसके अलावा, प्रोफाइलिंग से पता चला है कि वास्तव में, दिशाओं की खोज करते समय डेटा पढ़ना एक अड़चन नहीं है।

यदि हम ऐसे डेटा के बारे में बात कर रहे हैं जो गतिशील रूप से बदल सकते हैं, तो यहां बी-पेड़ प्रतिस्पर्धा से परे हैं। यह भी आवश्यक नहीं है कि पेड़ों का अपना कार्यान्वयन हो, आप SQL भंडारण का उपयोग कर सकते हैं, और उपरोक्त संस्थाओं को केवल एक प्राथमिक कुंजी से युक्त तालिकाओं के रूप में परिभाषित किया जा सकता है। तो, वर्णित इंजन के पूर्ववर्तियों में से एक को OpenLink Virtuoso DBMS के आधार पर बनाया गया था, जहां तालिकाओं को खुद पेड़ों की तरह व्यवस्थित किया जाता है और हमारे मामले में, इस तरह के रूप में कोई डेटा दोहराव नहीं है (मतलब डेटा सूचकांक में तालिका से दोहराया गया है)।

स्मृति में एक ग्राफ का प्रतिनिधित्व

इस खंड में, हम वर्णन करते हैं कि मेमोरी में एक अनपैक्ड ग्राफ़ कैसा दिखता है।

1. मेमोरी में पूरा ग्राफ मौजूद नहीं हो सकता है। जैसा कि पहले ही उल्लेख किया गया है, यह टाइलों में भरी हुई है क्योंकि किसी को इस ग्राफ के कुछ हिस्सों की आवश्यकता है।

2. इसलिए, इस कैश की टाइल और धारक है। कैशिंग रणनीति कोई भी हो सकती है। हमारे पास यह एलआरयू (कम से कम हाल में प्रयुक्त) है।

3. मेमोरी में लोड की गई टाइल - इसमें उस डेटा के बारे में सारी जानकारी होती है जो इसके अंतरिक्ष क्षेत्र में गिर गई थी। जैसा कि पहले ही उल्लेख किया गया है, इसके लिए सभी मेमोरी टाइल से संबंधित आवंटनकर्ता से आवंटित की जाती है और उसकी मृत्यु पर मुक्त हो जाती है। अर्थात्:

struct vertex_t {int x_; int y_; const link_t*links_; };  ,   ..     .  links_      ,    . struct link_t { int64_tfid_; //    int len_; //  int class_; //  int vert_id_; //   , >0,      union { const vertex_t *vertex_; //         int tile_id_; //    }; const link_t *next_; //   }; struct restriction_t {uint64_t from_; uint64_t to_;};   .         ,   ( )         . ,   . 

4. इस प्रकार, मेमोरी में एक टाइल उपयोग के लिए तैयार किए गए ग्राफ़ का एक टुकड़ा है:

• अंक संख्या के आधार पर जारी करें
• वर्टेक्स द्वारा आउटगोइंग किनारों का पता लगाएं
• उस पर प्रतिबंध के लिए पसलियों की एक जोड़ी का परीक्षण करें
• टाइल के अंदर जाने पर किनारे या तो नुकीले होते हैं, या अन्यथा टाइल-नंबर / वर्टेक्स-नंबर की जोड़ी। इस जोड़ी के लिए, ग्राफ़ के साथ आगे बढ़ने पर, आप पारदर्शी रूप से कैश धारक से आवश्यक टाइल पूछ सकते हैं, यदि आवश्यक हो तो इसे लोड कर सकते हैं और इसे स्विच कर सकते हैं।

वास्तव में खोज

1. खोज शुरू करने से पहले, आपको ग्राफ को संलग्न करना होगा। यानी बाहर हमें बिंदुओं के दो सेट मिलते हैं - स्रोत और अंत। प्रत्येक बिंदु का विवरण इसके बाहरी ग्राफ एज आइडेंटिफ़ायर और मूल्य के होते हैं। प्रारंभिक बिंदु के लिए इस किनारे की शुरुआत तक पहुंचने की लागत और अंत बिंदु के लिए किनारे के अंत से अंतिम तक पथ की लागत। तो:

2. पहचानकर्ताओं के पेड़ का उपयोग करते हुए, हम किनारों के पहचानकर्ता को ग्राफ में प्रवेश बिंदुओं में बदलते हैं (const ver__t *)। ऐसा करने के लिए, आपको टाइल कैश धारक से संपर्क करना होगा और आवश्यक लोड करना होगा।
हमें एक वस्तु की आवश्यकता है - फ़ाइनल के बारे में जानकारी रखने वाला, जिसमें टाइल पहचानकर्ता और शीर्ष संख्याएँ शामिल हैं। इस ऑब्जेक्ट के पास एक और उपयोगी जानकारी फिनिश लाइन की ज्यामितीय स्थिति है। यह स्पष्ट रूप से सेट किया जा सकता है, लेकिन गणना की जा सकती है, उदाहरण के लिए, अंतिम बिंदुओं के केंद्र के रूप में। एल्गोरिथ्म ए * के लिए पहुंची चोटी की लागत के अनुमानित भाग की गणना करने के लिए हमें इस बिंदु की आवश्यकता होगी

3. अब हमें एक "लहर" धारक की आवश्यकता है। इसमें निम्न शामिल हैं:

एक। एलोकेटर, वेल, उसके बिना कहाँ।
ख। भरी हुई टाइल्स का एक सेट। एक उचित आकार के रेखांकन के लिए, थोड़ा सा मुखौटा पर्याप्त है। यही है, जब हम पहली बार टाइल मारते हैं, तो इस मास्क में संबंधित बिट को चिह्नित करें और इसके लिंक के काउंटर को बढ़ाएं। खोज को पूरा करने के बाद, इस मास्क पर ध्यान केंद्रित करते हुए, हम वापस लिंक काउंट को वापस रोल करेंगे। इसी समय, जिन टाइलों के काउंटर शून्य पर रीसेट किए जाते हैं, उन्हें भविष्य में कैश से बाहर निकलने का मौका मिलता है।
सी। प्राथमिकता कतार। हम एक बाइनरी सॉर्टिंग हीप का उपयोग करते हैं। देखने के लिए कतार के उम्मीदवार। उदाहरण के लिए, शुरुआती बिंदु यहां सीधे जाते हैं। की दूरी तय की गई दूरी या खर्च किया गया समय है। और मान पारित बिंदु के विवरणक के लिए एक संकेतक है
घ। पारित बिंदुओं का एक सेट। इस तरह के प्रत्येक बिंदु को संरचना द्वारा वर्णित किया गया है:

 struct vertex_ptr_t { int64_t fid_; //   ,      //     0 const vertex_t *ptr_; //      const vertex_ptr_t *prev_; //      size_t cost_len_; //      size_t cost_time_; //      }; 

बेशक, ये संरचनाएं एक आवंटनकर्ता के रूप में बाहर खड़ी हैं।

4. इसलिए, प्रत्येक शुरुआती बिंदु के लिए हम इसका डिस्क्रिप्टर बनाते हैं और इसे एक ढेर में रखते हैं। इसलिए हम खोज शुरू करने के लिए तैयार हैं।

5. जबकि ढेर में कुछ है (और जबकि यह पहले से पाए गए उम्मीदवारों की तुलना में कुछ बेहतर है), हम इसमें से सबसे सस्ता तत्व चुनते हैं:

एक। इसके आउटगोइंग किनारों की सूची और उनमें से प्रत्येक के लिए दौड़ें:

I. पिछले एक से इस किनारे पर स्विच करने की संभावना की जांच करें।
द्वितीय। ग्राफ़ का शीर्ष ज्ञात करें, जो इस किनारे को इंगित करता है। शायद यह एक नई टाइल को लोड करेगा, और यह बिंदु इसमें होगा।
III. इस नए बिंदु को प्राप्त करने की लागत को कम करें। ऐसा करने के लिए:

1. संचित पथ और समय ले लो
2. वर्तमान किनारे की लंबाई के साथ पथ को सारांशित करें
3. हम अपनी लंबाई, प्रकार और कुछ के अनुसार वर्तमान को दूर करने के लिए आवश्यक राशि से समय बढ़ाते हैं
4. शेष पथ का अनुमान लगाएं और जोड़ दें - abs (dx) + abs (डाई), जहां dx और dy क्रमशः देशांतर और अक्षांश में अंतर रखते हैं
5. हम शेष पथ के अनुमान, दिन के समय, औसत गति पर आधारित फिनिश लाइन तक शेष समय का अनुमान लगाते हैं और जोड़ते हैं
6. पारित चरण और कुछ भी

चतुर्थ। पास किए गए शीर्ष के डिस्क्रिप्टर को बनाएं और भरें
वी। जांचें कि क्या यह बिंदु अंतिम नहीं है
छठी। यदि यह फिनिश लाइन है, तो हम पिछले की सूची को खोलते हैं
(vertex_ptr_t :: prev_) , इस बिंदु से शुरू होकर, जब तक हम 0 से टकराते हैं ,
यानी शुरू करने के लिए। यहां प्रत्यर्पण के लिए तैयार उम्मीदवार है।
सातवीं। बनाए गए डिस्क्रिप्टर को एक ढेर में रखें

परिणाम

आइए हमारी विशाल मातृभूमि की राजधानी के रोड ग्राफ के उदाहरण पर विलेख के परिणामों का मूल्यांकन करने का प्रयास करें।

• ग्राफ में 307,338 कोने हैं
• और 806220 पसलियाँ।
• अत्यधिक आयाम - 92 x 112 किमी
• टाइल्स की संख्या - 46 x 56 = 2576 टुकड़े
• रोड ग्राफ 13 980 केबी द्वारा कब्जा किए गए डिस्क पर डेटा की कुल मात्रा
• औसत मार्ग की लंबाई - 32.8 किमी
• उदाहरण के लिए

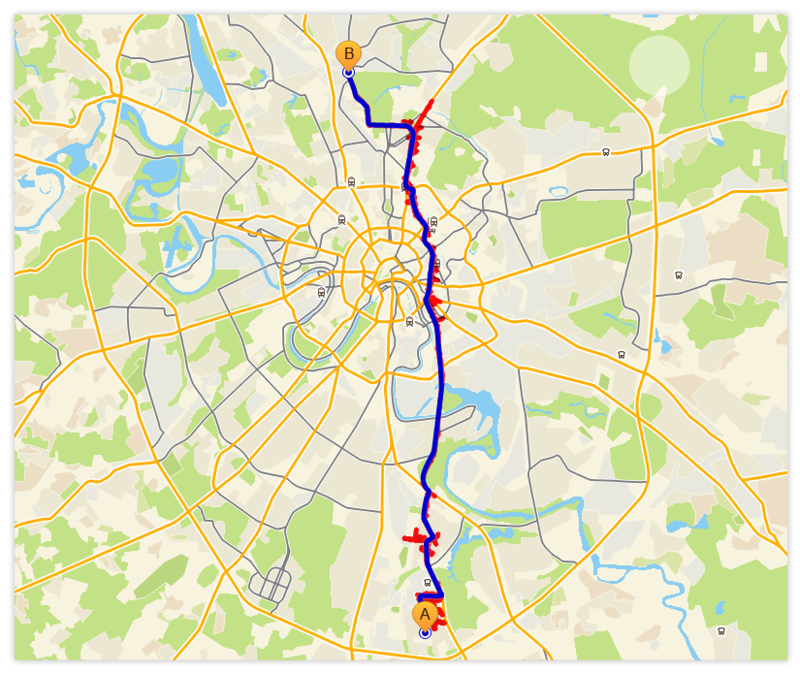
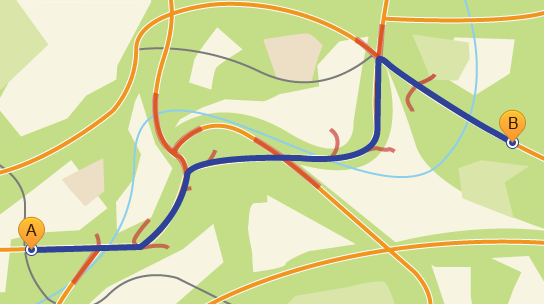
ब्लू इष्टतम मार्ग को इंगित करता है, लाल - "लहर"।

• वहीं, 22 टाइल्स पर औसतन 1,644 चोटियां और 2,406 किनारे पड़े हुए हैं
• इसके लिए टाइल्स के लिए 2096 केबी और लहर के लिए 116 केबी की जरूरत होती है
• Sony Xperia S 400 + 500 (इंडेक्स इनिशियलाइज़ेशन के लिए) ms (IPhone 4 800 + 1000 (...) ms) पर व्यतीत समय
• उदाहरण, पूरे ग्राफ के माध्यम से पथ

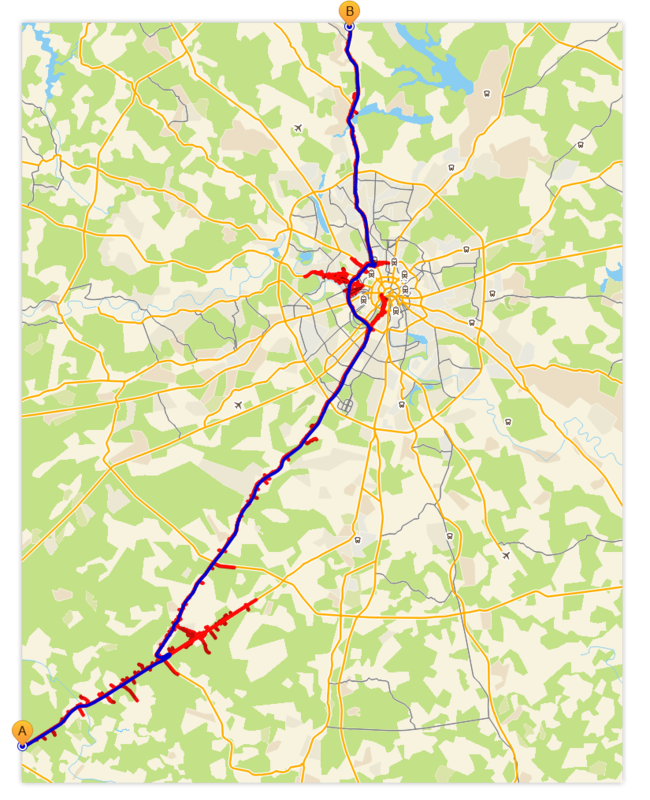
पहले की तरह, नीला इष्टतम मार्ग को इंगित करता है, लाल - "लहर"।
यह अवलोकन करने के लिए मनोरंजक है कि खोज ने ग्राफ़ के वास्तविक (अंतर्निहित, अंतर्निहित) पदानुक्रमित संरचना को कैसे प्रकट किया और इसका उपयोग करना शुरू किया

• इसकी गणना की लंबाई 135.3 किमी है।
• इस मामले में, 120 टाइलों पर पड़ी 2251 चोटियाँ और 3044 किनारे प्रभावित होते हैं
• इसी समय, टाइल्स के लिए 3,946 केबी और लहर के लिए 133 केबी की आवश्यकता होती है।
• समय 400 एमएस सोनी एक्सपीरिया एस (500 आईफोन 4) के साथ-साथ सूचकांक के एक ही समय लोड करने के लिए निश्चित रूप से बिताया
• और यहाँ यह प्रदर्शित किया जाता है कि विभिन्न सेटिंग्स के साथ नोवोसिबिर्स्क के माध्यम से ड्राइविंग के तीन चित्र कितना महत्वपूर्ण है।

कुल मिलाकर

जैसा कि हम देख सकते हैं, इस तरह की एक सरल डेटा संरचना और वर्णित एल्गोरिथ्म एक साधारण स्मार्टफोन पर एक बड़े शहर के एकल-स्तरीय ग्राफ के साथ काम करना संभव बनाता है। और अगर रैम हमें अनुमति देता है, उदाहरण के लिए, सर्वर के मामले में, टाइल कैश के आकार को बढ़ाते हुए, हम बस पूरे ग्राफ को मेमोरी में ड्राइव करते हैं और इसके तैयार प्रतिनिधित्व के साथ काम करते हैं। जिसका प्रदर्शन पर लाभकारी प्रभाव पड़ता है।

हमने जानबूझकर कुछ बिंदुओं को नहीं छुआ है, उदाहरण के लिए, ट्रैफ़िक स्थिति को ध्यान में रखते हुए, उसके बाद की भविष्यवाणी, पदानुक्रमित ग्राफ़, इसके लिए एक पूरी तरह से अलग कहानी है।

वह सब लोग है!