पिछली गणना किए बिना पाई के Nth संकेत की गणना

हाल ही में, पाई नंबर की गणना के लिए एक सुरुचिपूर्ण सूत्र है, जो पहली बार 1995 में डेविड बेली, पीटर बोरविन और साइमन प्लफ द्वारा प्रकाशित किया गया था:


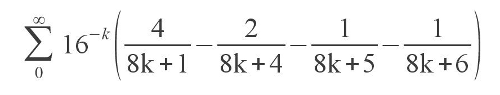
यह प्रतीत होता है: इसके बारे में क्या खास है - पाई की गणना के लिए एक महान कई सूत्र हैं: स्कूल मोंटे कार्लो विधि से मायावी पॉइसन अभिन्न और फ्रेंकोइस विएत फॉर्मूला देर से मध्य युग से। लेकिन यह इस फॉर्मूले पर ठीक है कि विशेष ध्यान दिया जाना चाहिए - यह आपको पिछले वाले को खोजने के बिना पाई के एनटी चिन्ह की गणना करने की अनुमति देता है। यह कैसे काम करता है, इसके बारे में जानकारी के लिए, साथ ही साथ तैयार सी भाषा कोड जो 1,000,000 वें वर्ण की गणना करता है, मैं एक हैराकैट के लिए पूछता हूं।

Pi काम के Nth संकेत की गणना के लिए एल्गोरिथ्म कैसे करता है?
उदाहरण के लिए, यदि हमें Pi के 1000 वें हेक्साडेसिमल चिन्ह की आवश्यकता है, तो हम पूरे सूत्र को 16 ^ 1000 से गुणा करते हैं, जिससे कोष्ठक के सामने कारक 16 ^ (1000-k) तक उलट हो जाता है। जब घातांक, हम द्विआधारी घातांक एल्गोरिथ्म का उपयोग करते हैं या, जैसा कि नीचे दिए गए उदाहरण में दिखाया जाएगा, घातांक मोडुलो । उसके बाद, हम श्रृंखला के कई सदस्यों के योग की गणना करते हैं। इसके अलावा, बहुत गणना करने के लिए आवश्यक नहीं है: जैसे कि k बढ़ता है, 16 ^ (Nk) जल्दी से घटता है, ताकि बाद की शर्तें वांछित अंकों के मूल्य को प्रभावित न करें)। यह सब जादू है - सरल और सरल।

बेली-बोरविन-पफ फॉर्मूला साइमन पफ द्वारा पीएसएलक्यू एल्गोरिथ्म का उपयोग करके पाया गया था, जो 2000 में सेंचुरी सूची के शीर्ष 10 एल्गोरिदम में शामिल था। PSLQ एल्गोरिथम स्वयं बेली द्वारा विकसित किया गया था। यहां गणितज्ञों के बारे में एक मैक्सिकन श्रृंखला है।
वैसे, एल्गोरिथ्म का चलने का समय ओ (एन) है, मेमोरी उपयोग ओ (लॉग एन) है, जहां एन वांछित चरित्र का सीरियल नंबर है।

मुझे लगता है कि एल्गोरिथ्म के लेखक डेविड बेली द्वारा सीधे सी में लिखे गए कोड का हवाला देना उचित होगा:

/* This program implements the BBP algorithm to generate a few hexadecimal digits beginning immediately after a given position id, or in other words beginning at position id + 1. On most systems using IEEE 64-bit floating- point arithmetic, this code works correctly so long as d is less than approximately 1.18 x 10^7. If 80-bit arithmetic can be employed, this limit is significantly higher. Whatever arithmetic is used, results for a given position id can be checked by repeating with id-1 or id+1, and verifying that the hex digits perfectly overlap with an offset of one, except possibly for a few trailing digits. The resulting fractions are typically accurate to at least 11 decimal digits, and to at least 9 hex digits. */ /* David H. Bailey 2006-09-08 */ #include <stdio.h> #include <math.h> int main() { double pid, s1, s2, s3, s4; double series (int m, int n); void ihex (double x, int m, char c[]); int id = 1000000; #define NHX 16 char chx[NHX]; /* id is the digit position. Digits generated follow immediately after id. */ s1 = series (1, id); s2 = series (4, id); s3 = series (5, id); s4 = series (6, id); pid = 4. * s1 - 2. * s2 - s3 - s4; pid = pid - (int) pid + 1.; ihex (pid, NHX, chx); printf (" position = %i\n fraction = %.15f \n hex digits = %10.10s\n", id, pid, chx); } void ihex (double x, int nhx, char chx[]) /* This returns, in chx, the first nhx hex digits of the fraction of x. */ { int i; double y; char hx[] = "0123456789ABCDEF"; y = fabs (x); for (i = 0; i < nhx; i++){ y = 16. * (y - floor (y)); chx[i] = hx[(int) y]; } } double series (int m, int id) /* This routine evaluates the series sum_k 16^(id-k)/(8*k+m) using the modular exponentiation technique. */ { int k; double ak, eps, p, s, t; double expm (double x, double y); #define eps 1e-17 s = 0.; /* Sum the series up to id. */ for (k = 0; k < id; k++){ ak = 8 * k + m; p = id - k; t = expm (p, ak); s = s + t / ak; s = s - (int) s; } /* Compute a few terms where k >= id. */ for (k = id; k <= id + 100; k++){ ak = 8 * k + m; t = pow (16., (double) (id - k)) / ak; if (t < eps) break; s = s + t; s = s - (int) s; } return s; } double expm (double p, double ak) /* expm = 16^p mod ak. This routine uses the left-to-right binary exponentiation scheme. */ { int i, j; double p1, pt, r; #define ntp 25 static double tp[ntp]; static int tp1 = 0; /* If this is the first call to expm, fill the power of two table tp. */ if (tp1 == 0) { tp1 = 1; tp[0] = 1.; for (i = 1; i < ntp; i++) tp[i] = 2. * tp[i-1]; } if (ak == 1.) return 0.; /* Find the greatest power of two less than or equal to p. */ for (i = 0; i < ntp; i++) if (tp[i] > p) break; pt = tp[i-1]; p1 = p; r = 1.; /* Perform binary exponentiation algorithm modulo ak. */ for (j = 1; j <= i; j++){ if (p1 >= pt){ r = 16. * r; r = r - (int) (r / ak) * ak; p1 = p1 - pt; } pt = 0.5 * pt; if (pt >= 1.){ r = r * r; r = r - (int) (r / ak) * ak; } } return r; } 

यह क्या अवसर देता है? उदाहरण के लिए: हम एक वितरित कंप्यूटिंग सिस्टम बना सकते हैं जो पाई की संख्या की गणना करता है और गणना सटीकता के लिए पूरे हेब्रत के नए रिकॉर्ड को सेट करता है (जो कि अब, वैसे, 10 ट्रिलियन दशमलव स्थान है)। अनुभवजन्य आंकड़ों के अनुसार, पीआई संख्या का आंशिक हिस्सा एक सामान्य संख्यात्मक अनुक्रम है (हालांकि यह अभी तक विश्वसनीय रूप से सिद्ध नहीं हुआ है), जिसका अर्थ है कि इससे प्राप्त अंकों के अनुक्रम पासवर्ड और सिर्फ यादृच्छिक संख्या, या क्रिप्टोग्राफिक एल्गोरिदम (उदाहरण के लिए, हैशिंग) में उत्पन्न किए जा सकते हैं। । इसका उपयोग करने के कई तरीके हैं - आपको बस अपनी कल्पना को चालू करने की आवश्यकता है।

आप डेविड बेली के एक लेख में विषय पर अधिक जानकारी पा सकते हैं, जहां वह एल्गोरिथ्म और इसके कार्यान्वयन ( पीडीएफ ) के बारे में विस्तार से बात करता है;

और ऐसा लगता है कि आप इस एल्गोरिथ्म के बारे में रनेट में पहला रूसी भाषा का लेख पढ़ते हैं - मैं दूसरों को नहीं ढूंढ सका।