🤱🏾 💪🏿 🥚 छिपी मार्कोव चेन, विटर्बी एल्गोरिदम 🐁 🌑 👩‍🔬

हमें एक झूठ डिटेक्टर को लागू करने की आवश्यकता है, जो किसी व्यक्ति के हाथों को कांपने से निर्धारित करता है कि वह सच कह रहा है या नहीं। मान लीजिए जब कोई व्यक्ति झूठ बोल रहा है, तो उसके हाथ थोड़ा और हिल रहे हैं। संकेत इस तरह हो सकता है:

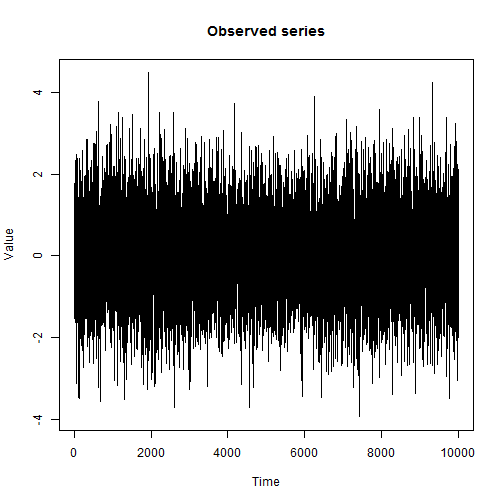
स्रोत संकेत

एलआर रैबनेर द्वारा लेख में एक दिलचस्प विधि "ए ट्यूटोरियल ऑन हिडेन मार्कोव मॉडल और स्पीच रिकॉग्निशन में चयनित एप्लिकेशन" में वर्णित है, जो मार्कोव छिपे हुए चेन मॉडल का परिचय देता है और तीन मूल्यवान एल्गोरिदम का वर्णन करता है: फॉरवर्ड-बैकवर्ड प्रक्रिया , विटर्बी एल्गोरिथम और बॉम-वेल्च रिस्टीमेशन । इस तथ्य के बावजूद कि ये एल्गोरिदम केवल समुच्चय में रुचि रखते हैं, एक बेहतर समझ के लिए, उन्हें अलग से वर्णन करना बेहतर है।

छिपी हुई मार्कोव श्रृंखला विधि का व्यापक रूप से उपयोग किया जाता है, उदाहरण के लिए, इसका उपयोग सीजी द्वीपों (डीएनए, आरएनए क्षेत्रों को साइटोसिन और ग्वानिन बाइंडिंग के उच्च घनत्व के साथ) की खोज के लिए किया जाता है, जबकि लॉरेंस राबिनर ने स्वयं भाषण मान्यता के लिए इसका उपयोग किया था। इलेक्ट्रोएन्सेफ़लोग्राम के अनुसार नींद / जाग के चरणों में परिवर्तन को ट्रैक करने और मिरगी के दौरे को देखने के लिए एल्गोरिदम मेरे लिए उपयोगी था।

छिपे हुए मार्कोव श्रृंखला के मॉडल में, यह माना जाता है कि प्रश्न में प्रणाली में निम्नलिखित गुण हैं:

प्रत्येक समय अवधि में, सिस्टम राज्यों के एक सीमित सेट में से एक में हो सकता है;
सिस्टम गलती से एक राज्य से दूसरे (संभवतः एक ही) पर स्विच करता है और संक्रमण की संभावना केवल उस राज्य पर निर्भर करता है जिसमें यह था;
समय के प्रत्येक क्षण में, सिस्टम एक विशेषीकृत मूल्य का एक मूल्य देता है - एक यादृच्छिक मूल्य जो केवल सिस्टम की वर्तमान स्थिति पर निर्भर करता है।

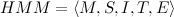
HMM मॉडल के रूप में वर्णित किया जा सकता है: $HMM = \ langle M, S, I, T, E \ rangle$

एम राज्यों की संख्या है;
$S = \ {S_1, ..., S_M \}$ - शर्तों का एक सीमित सेट;
$I = (P (q_0 = S_i) = \ pi_i)$ संभावनाओं का सदिश है कि सिस्टम 0 में समय पर राज्य में है;
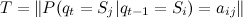$T = \ | P (q_t = S_j | q_ {t-1} = S_i) = a_ {ij} \ |$ राज्य i से राज्य j के लिए संक्रमण की संभावना मैट्रिक्स है $[1, T_m] में forall t \$ ;
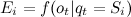। ओ पर परिभाषित घनत्व या वितरण के कार्यों (सभी राज्यों के लिए नमूदार मूल्यों का सेट) के रूप में परिभाषित प्रत्येक राज्यों के अनुरूप अवलोकन योग्य यादृच्छिक चर के वितरण का वेक्टर है।

समय टी को असतत माना जाता है, गैर-नकारात्मक पूर्णांकों द्वारा दिया जाता है, जहां 0 समय के प्रारंभिक क्षण से मेल खाती है, और टीएम सबसे बड़े मूल्य पर।

जब हमारे पास 2 छिपे हुए राज्य हैं, और देखे गए मान विभिन्न वितरणों के साथ सामान्य वितरण का पालन करते हैं, जैसे कि झूठ डिटेक्टर के साथ उदाहरण में, प्रत्येक राज्य के लिए सिस्टम कार्यप्रणाली एल्गोरिदम को निम्नानुसार दर्शाया जा सकता है:
छिपी हुई मार्कोव श्रृंखला की योजना

एक सरल विवरण पहले से ही प्रोबेबिलिस्टिक मॉडल: उदाहरण और चित्रों में वर्णित किया गया है।

प्रेक्षित मात्राओं के वितरण के वेक्टर का विकल्प अक्सर शोधकर्ता के पास होता है। आदर्श रूप में, देखी गई मात्रा एक अव्यक्त अवस्था है, और इस स्थिति में इन राज्यों को निर्धारित करने का कार्य तुच्छ हो जाता है। वास्तव में, सब कुछ अधिक जटिल है, उदाहरण के लिए, राबिनर द्वारा वर्णित शास्त्रीय मॉडल का सुझाव है कि E_i

- परिमित असतत वितरण। नीचे दिए गए ग्राफ़ में कुछ ऐसा है:

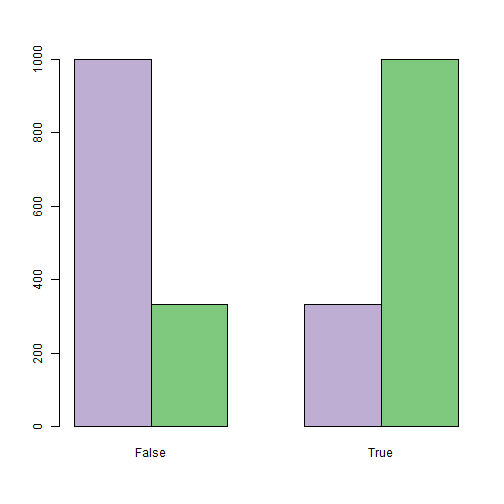
शोधकर्ता को आमतौर पर प्रेक्षित राज्यों के वितरण को चुनने में स्वतंत्रता होती है। प्रेक्षित मान छिपे हुए राज्यों को अलग करता है, बेहतर है। एक प्रोग्रामिंग दृष्टिकोण से, विभिन्न अवलोकन योग्य विशेषताओं की गणना करने का मतलब है कि सावधानीपूर्वक इनकैप्सुलेशन की आवश्यकता है E_i

। नीचे दिया गया ग्राफ़ झूठ पकड़ने की समस्या के लिए प्रारंभिक डेटा का एक उदाहरण दिखाता है, जहां मनाया विशेषता (हाथ मिलाना) का वितरण निरंतर है, क्योंकि यह दोनों राज्यों के लिए 0 के औसत के साथ सामान्य रूप से मॉडलिंग की गई थी, 1 के फैलाव के साथ जब कोई व्यक्ति सच बता रहा है (बैंगनी कॉलम) और 1.21 झूठ बोलने पर (हरे रंग का कॉलम):

मॉडल स्थापित करने के मुद्दों पर नहीं छूने के लिए, हम एक सरलीकृत कार्य पर विचार करते हैं।

दिए गए:

दो छिपे हुए राज्य, जहां निष्पक्ष व्यवहार 1 के फैलाव के साथ सफेद शोर से मेल खाता है, झूठ - 1.21 के फैलाव के साथ सफेद शोर;
लगातार 10,000 टिप्पणियों ओ का नमूना;
राज्य का परिवर्तन औसतन हर 2,500 चक्रों में एक बार होता है।
राज्य संक्रमण के क्षणों को निर्धारित करना आवश्यक है।

समाधान:

चलो मॉडल के पांच मापदंडों को निर्धारित करते हैं:

राज्यों की संख्या M = 2;
एस = {1,2};
अनुभव से पता चलता है कि प्रारंभिक वितरण व्यावहारिक रूप से अप्रासंगिक है, इसलिए I = (0.5,0.5);
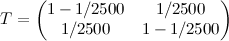$T \ leftarrow \ left (\ start {मैट्रिक्स} 1-1 / 2500 और 1/2500 \\ 1/2500 & 1-1 / 2500 \ end {मैट्रिक्स} \ right)$ ;
ई = (एन (0,1), एन (0,1.21))।

हम दिए गए मॉडल मापदंडों के लिए Viterbi एल्गोरिथ्म का उपयोग करते हुए समय में प्रत्येक क्षण के लिए सबसे प्रशंसनीय स्थिति पाते हैं।
मॉडल को निर्दिष्ट करने और विटर्बी एल्गोरिथ्म को चलाने के लिए समस्या का समाधान कम हो गया है।

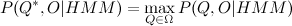
छिपी हुई मार्कोव श्रृंखला के मॉडल और प्रेक्षित विशेषताओं के मूल्यों के नमूने के अनुसार, हम राज्यों का एक क्रम पाते हैं जो किसी दिए गए मॉडल में नमूने का सबसे अच्छा वर्णन करेंगे। अवधारणा को विभिन्न तरीकों से सबसे अच्छी तरह से व्याख्या की जा सकती है, लेकिन अच्छी तरह से स्थापित समाधान विटर्बी एल्गोरिदम है, जो इस तरह के अनुक्रम को ढूंढता है $Q ^ * = (q_0, .., q_ {T_m}), S में q_i \$ कि $P (Q ^ *, O | HMM) = \ max \ limit_ {Q \ in \ Omega} P (Q, O (HMM))$ ।

खोज कार्य क्यू ^ *

गतिशील प्रोग्रामिंग का उपयोग करके हल किया गया, इसके लिए हम फ़ंक्शन पर विचार करते हैं:

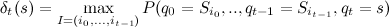
$\ delta_t (s) = \ max \ limit_ {I = (i_0, ..., i_ {t-1}})} P (q_0 = S_ {i_0}, .., q_ {t-1}} S_ {i_ {t-1}}, q_t = s)$
जहाँ $\ delta_t (s)$ क्या समय टी में राज्य के होने की सबसे बड़ी संभावना है। पुनरावर्ती रूप से, इस फ़ंक्शन को निम्नानुसार परिभाषित किया जा सकता है:

$\ delta_0 (s) = \ pi_s f_s (o_0), \ delta_t (s) = \ max_ {s 'में S} (\ delta_ {t-1} (s)) a_ {s's} (o_t)$
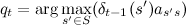
इसके साथ ही गणना के साथ $\ delta_t (s)$ समय के प्रत्येक क्षण के लिए, हम सबसे संभावित स्थिति को याद करते हैं जिसमें से हम आए थे, अर्थात्। $q_t = \ arg \ max \ limit_ {s 'में S} (\ delta_ {t-1} (s)) a_ {s's})$ जिस पर अधिकतम पहुंच गया था। उसी समय $q_ {T_m} = \ arg \ max \ limit_ {s \ _ S} (\ delta_ {T_m} (s))$ , और इसलिए आप पुनर्स्थापित कर सकते हैं $क्यू ^ * = (q_0 ^ *, ..., q_ {T_m} ^ *)$ रिवर्स ऑर्डर में उनके माध्यम से चलना। आप देख सकते हैं कि $\ 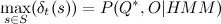max \ limit_ {s \ _ S} (\ delta_ {t} (s)) = P (Q * *, O | HMM) |$ वांछित संभावना का मूल्य है। आवश्यक क्रम क्यू ^ *

पाया। एल्गोरिथ्म की एक दिलचस्प संपत्ति यह है कि मनाया विशेषताओं का अनुमानित कार्य इसमें शामिल है $\ delta_t (s)$ एक कारक के रूप में। अगर हम ऐसा मान लें

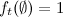
, फिर टिप्पणियों में चूक के मामले में, इन क्षणों में सबसे संभावित अव्यक्त अवस्थाओं का मूल्यांकन करना अभी भी संभव है।

विटर्बी के एल्गोरिथ्म के लिए छद्म कोड नीचे उल्लिखित है। यह ध्यान दिया जाना चाहिए कि वैक्टर और मैट्रिस के साथ सभी ऑपरेशन तत्व-वार हैं ।

Tm<-10000 # Max time M<-2 # Number of states S<-seq(from=1, to=M) # States [1,2] I<-rep(1./M, each=M) # Initial distribution [0.5, 0.5] T<-matrix(c(1-4./Tm, 4./Tm, 4./Tm,1-4./Tm),2) #[0.9995 0.0005; 0.0005 0.9995] P<-c(function(o){dnorm(o)}, function(o){dnorm(o,sd=1.1)}) # Vector of density functions for each state (N(0,1), N(0,1.21)) E<-function(P,s,o){P[[s]](o)} # Calculate probability of observed value o for state s. Es<-function(E,P,o) { # Same for all states probs<-c() for(s in S) { probs<-append(probs, E(P,s,o)) } return(probs) } viterbi<-function(S,I,T,P,E,O,tm) { delta<-I*Es(E,P,O[1]) # initialization for t=1 prev_states<-cbind(rep(0,length(S))) # zeros for(t in 2:Tm) { m<-matrix(rep(delta,length(S)),length(S))*T # delta(s')*T[ss'] forall s,s' md<-apply(m,2,max) # search for max delta(s) by s' for all s max_delta<-apply(m,2,which.max) prev_states<-cbind(prev_states,max_delta) delta<-md*Es(E,P,O[t]) # prepare next step delta(s) } return(list(delta=delta,ps=prev_states)) # return delta_Tm(s) and paths } restoreStates<-function(d,prev_states) { idx<-which.max(d) s<-c(idx) sz<-length(prev_states[1,]) for(i in sz:2) { idx<-prev_states[idx,i] s<-append(s,idx,after=0) } return (as.vector(s)) }

कोई इस "छद्म कोड" में आर कोड को पहचान सकता है, लेकिन यह सबसे अच्छा कार्यान्वयन से दूर है।

उन राज्यों के कब्ज़ की अवधि की तुलना करें जो सिमुलेशन (ग्राफ़ के ऊपरी भाग) के दौरान सेट किए गए थे और जो विटर्बी एल्गोरिथ्म (ग्राफ़ के निचले हिस्से) का उपयोग करते हुए पाए गए थे:

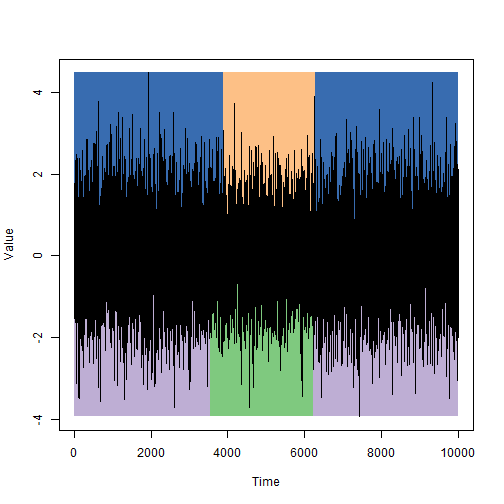
यह मेरी राय में काफी योग्य है, लेकिन हर बार आपको इसके लिए उम्मीद नहीं करनी चाहिए।

पहले वर्णित Viterbi एल्गोरिथ्म को एक छिपे हुए मार्कोव श्रृंखला मॉडल (viterbi फ़ंक्शन के तर्क) की परिभाषा की आवश्यकता है। उन्हें सेट करने के लिए, एक साधारण इनिशियलाइज़ेशन का उपयोग किया जाता है, जिसका तात्पर्य है कि O के देखे गए मानों के चयन के अलावा, Q के छिपे हुए राज्यों का एक समान चयन जिसे हम कहीं से जानते हैं, भी दिया गया है। इस मामले में, मापदंडों के मूल्यांकन के सूत्र इस तरह दिखेंगे:
$S \ leftarrow \ left \ {s: q_t = s, t \ में [0, T_m] \ right \} \\ M \ leftarrow \ | S \ | \\ I \ leftarrow \ left (\ 0, T_m] में {frac {\ _ sum_ {t \ _}} Id (q_t = s)} {T_m + 1}, s \ _ S \ right में) \\ T's leftarrow \ left [[1, T_m] {आईडी (q_ {t-1} = s ', q_t = s)} {\ _ sum_ {t \ _ in [0, T_m]} (\ sum_ {) t \ _ [1, T_m]} Id (q_ {t-1} = s ')}, s, s' \ _ S \ right में) \\ E \ leftarrow \ बाएँ (f_s (o_t) = \ _rac {\ _) sum_ {t \ in [0, T_m]} Id (q_t = s, o_t = e)} {\ sum_ {t \ in [0, T_m]} Id (q_t = s)}, s \ _ S \ right में)$
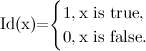
जहाँ Id (x) एक संकेतक फ़ंक्शन है, $Id (x) = \ start {case} 1, \ mbox {x is true}, \\ 0, \ mbox \ x x गलत है।} \ end {केस}।$

माना झूठ डिटेक्टर उदाहरण के लिए, एल्गोरिथ्म ने 10,000 राज्यों (~ 4%) में से 413 को गलत तरीके से वर्गीकृत किया, जो बिल्कुल भी बुरा नहीं है। विटर्बी एल्गोरिथ्म अव्यक्त अवस्थाओं में बदलाव के क्षणों को अच्छी सटीकता के साथ पता लगाने में सक्षम है, लेकिन केवल अगर मनाया विशेषताओं के वितरण को ठीक से जाना जाता है। यदि केवल ऐसे वितरण के पैरामीट्रिक वर्ग को जाना जाता है, तो सबसे उपयुक्त मापदंडों का चयन करने का एक तरीका है, जिसे बॉम-वेल्श एल्गोरिथम कहा जाता है।

यदि दिलचस्पी है, तो अधिक के लिए पूछें ...

छिपी मार्कोव चेन, विटर्बी एल्गोरिदम

More articles: