Mazes उत्पन्न करने के लिए एक असामान्य तरीका है

इस लेख में मैं mazes पैदा करने के लिए एक असामान्य दृष्टिकोण के बारे में बात करूंगा। यह सेरेब्रल कॉर्टेक्स के अमेरी न्यूरोनल गतिविधि के मॉडल पर आधारित है, जो तंत्रिका नेटवर्क का एक निरंतर एनालॉग है। कुछ शर्तों के तहत, यह आपको बहुत जटिल आकार के सुंदर लेबिरिंथ बनाने की अनुमति देता है, जो तस्वीर में दिखाया गया है।

आपको बहुत सारे विश्लेषण और कुछ निजी व्युत्पन्न मिलेंगे। कोड संलग्न है।
मैं कटौती के लिए पूछना!

परिचय

कई पाठकों ने पहले से ही एक या दूसरे रूप में एक भूलभुलैया पैदा करने की समस्या का सामना किया है और जानते हैं कि इसे हल करने के लिए, वे अक्सर एक ग्राफ में न्यूनतम फैले हुए पेड़ को खोजने के लिए प्राइमा और क्रुस्क्ल एल्गोरिदम का उपयोग करते हैं, जिसके कोने भूलभुलैया की कोशिकाएं हैं और किनारों आसन्न कोशिकाओं के बीच मार्ग का प्रतिनिधित्व करते हैं। हम ग्राफ सिद्धांत से एक बोल्ड कदम ... कम्प्यूटेशनल न्यूरोबायोलॉजी की ओर ले जाएंगे।

20 वीं शताब्दी के दौरान, वैज्ञानिकों ने एकल न्यूरॉन्स (तंत्रिका तंत्र की कोशिकाओं) के गणितीय मॉडल और उनकी बातचीत का निर्माण किया। 1975 में, एस। अमारी ने सेरेब्रल कॉर्टेक्स के अपने निरंतर मॉडल के प्रकाश का परिचय दिया। इसमें, तंत्रिका तंत्र को एक सतत माध्यम माना जाता था, जिसके प्रत्येक बिंदु पर एक "न्यूरॉन" होता है, जिसकी झिल्ली की क्षमता की विशेषता होती है, जो पड़ोसी न्यूरॉन्स और बाहरी उत्तेजनाओं के साथ शुल्क का आदान-प्रदान करके अपनी क्षमता को बदलता है। अमारी का मॉडल मानव दृष्टि की कई घटनाओं की व्याख्या करने के लिए प्रसिद्ध है, विशेष रूप से, मनोवैज्ञानिक पदार्थों के कारण दृश्य मतिभ्रम।

अमारी का मॉडल, अपने सरलतम रूप में, एक पूर्णांक-विभेदक समीकरण के लिए कैची समस्या है:

यहाँ आप स्पष्टीकरण के बिना नहीं कर सकते:

• बिंदु पर न्यूरॉन की झिल्ली की क्षमता का वास्तविक मूल्य है समय पर ।
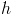• बाकी क्षमता (कुछ वास्तविक स्थिर)।
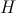• - हेडवाइड कदम समारोह:

  

• - वजन समारोह।
• - बाहरी अड़चन।
• - समय के प्रारंभिक क्षण में क्षमता का वितरण।
• - क्षेत्र का मनमाना बिंदु जिस पर क्षमता निर्धारित की जाती है। चूंकि हम भूलभुलैया की दो-आयामी छवि उत्पन्न करने की योजना बनाते हैं, जैसा कि हम पूरे वास्तविक विमान पर विचार करेंगे।
• निजी व्युत्पन्न 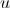बाईं ओर समय में क्षमता में तात्कालिक परिवर्तन को इंगित करता है 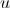। दाहिना भाग इस परिवर्तन के लिए नियम निर्धारित करता है।
• दाईं ओर पहले दो शब्दों का अर्थ है कि, उत्तेजनाओं की अनुपस्थिति में, संभावित मूल्य आराम करने की क्षमता के मूल्य को दर्शाता है।
• निम्नलिखित शब्द पड़ोसी न्यूरॉन्स के प्रभाव को ध्यान में रखते हैं। हीविसाइड फ़ंक्शन एक न्यूरॉन के सक्रियण समारोह की भूमिका निभाता है: एक न्यूरॉन अपने पड़ोसियों को केवल तभी प्रभावित करना शुरू करता है जब उसकी क्षमता शून्य से अधिक हो। हम आगे ऐसे न्यूरॉन्स को सक्रिय कहेंगे, और सकारात्मक क्षमता वाले बिंदुओं के सेट को गतिविधि का क्षेत्र कहा जाता है। यह स्पष्ट है कि आराम करने वाले न्यूरॉन्स सक्रिय नहीं होने चाहिए, अर्थात, आराम करने की क्षमता सकारात्मक नहीं होनी चाहिए। सक्रिय पड़ोसियों को दो समूहों में विभाजित किया जा सकता है: उत्तेजक और निरोधात्मक। उत्तेजक न्यूरॉन्स पड़ोसियों की क्षमता में वृद्धि करते हैं, और निरोधात्मक न्यूरॉन्स कम हो जाते हैं। इसी समय, exciters एक छोटे से पड़ोस में गतिविधि का एक शक्तिशाली उछाल बनाते हैं, जबकि निरोधात्मक धीरे-धीरे एक बड़े दायरे के आसपास के क्षेत्र में गतिविधि को बुझाते हैं। यह तथ्य वजन समारोह की पसंद में परिलक्षित होता है। "मैक्सिकन टोपी" के रूप में:

  
  

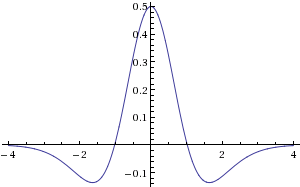
• समीकरण के दाईं ओर अंतिम शब्द बाहरी उत्तेजना की कार्रवाई को ध्यान में रखता है। उदाहरण के लिए, मस्तिष्क के दृश्य प्रांतस्था के लिए, एक प्राकृतिक उत्तेजना रेटिना से प्राप्त एक संकेत है। हम मानते हैं कि उत्तेजना एक गैर-नकारात्मक स्थिर (समय-स्वतंत्र) फ़ंक्शन द्वारा दी गई है।

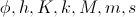
हम खुद से एक सवाल पूछते हैं: क्या मॉडल मापदंडों को चुनना संभव है ताकि इसका स्थिर समाधान (के लिए) ) कुछ भूलभुलैया की एक छवि थी?

अमारी मॉडल सॉल्यूशन गुण

अमारी मॉडल के समाधानों का विश्लेषण करने के लिए, हमें एक आयामी मामले पर विचार करने के लिए खुद को सीमित करने के लिए पर्याप्त होगा। सादगी के लिए, हम यह मानते हैं पूरी लाइन पर स्थिर।
सबसे पहले, हम तथाकथित टक्कर समाधानों में रुचि रखते हैं। वे उल्लेखनीय हैं कि वे कुछ परिमित अंतराल पर ही सकारात्मक हैं चलती सीमाओं के साथ। उनके लिए अमारी समीकरण इस प्रकार लिखा गया है:

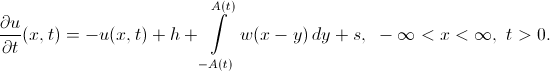
यह समझने के लिए कि इसका समाधान कैसे व्यवहार करता है, हम फ़ंक्शन का परिचय देते हैं

अब उसी समीकरण को फिर से लिखा जा सकता है:

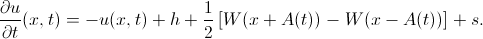
हम जानते हैं कि गतिविधि अंतराल की सीमाओं पर टकराव का समाधान गायब हो जाता है (इसलिए उन्हें सीमा कहा जाता है)। हम इस सीमा को सही सीमा पर लिखते हैं:

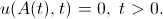
अब हम चर के संबंध में अंतिम पहचान को अलग करते हैं :

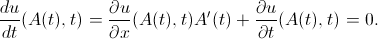
यहाँ से:

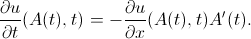
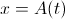
के लिए टक्कर समाधान के लिए समीकरण में अंतिम अभिव्यक्ति को प्रतिस्थापित करना हमें मिलता है:

अब ध्यान दें कि सम्मान के साथ आंशिक व्युत्पन्न बाईं ओर हमेशा नकारात्मक होता है, क्योंकि दाईं सीमा के बाईं ओर का समाधान शून्य से अधिक है, और इसके दाईं ओर, कम है। इसलिये

इस प्रकार, सीमा के बदलाव की दिशा केवल दाईं ओर अभिव्यक्ति के मूल्य पर निर्भर करती है। यदि यह शून्य से अधिक है, तो गतिविधि का क्षेत्र फैलता है; यदि कम होता है, तो यह संकीर्ण होता है। यदि शून्य, संतुलन पर पहुंच गया है।
संभावित फ़ंक्शन ग्राफ़ पर एक नज़र डालें। ।

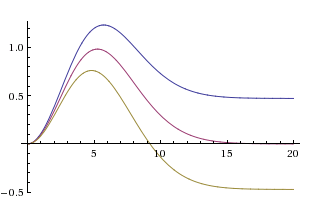
जाहिर है, दो मामले संभव हैं:

1. सीमा मान गैर नकारात्मक। फिर बम्प समाधान की गतिविधि का क्षेत्र असीमित रूप से विस्तारित होगा।
2. सीमा मान नकारात्मक। तब गतिविधि का क्षेत्र सीमित हो जाएगा। इसके अलावा, इस मामले में यह दिखाया जा सकता है कि समाधान के गतिविधि क्षेत्र के अमारी समीकरण में जुड़े घटक कभी भी विलय नहीं करते हैं ।

दुर्भाग्य से, दो आयामी मामले में, फ़ंक्शन के लिए एक स्पष्ट अभिव्यक्ति प्राप्त करना कठिन है, इसलिए हम इसका मूल्यांकन करते हैं:

यहाँ से:

भूलभुलैया पीढ़ी

आवश्यक ज्ञान का सामान एकत्र करने के बाद, हम शुरू कर सकते हैं, वास्तव में, भूलभुलैया उत्पन्न करने के लिए एल्गोरिथ्म।
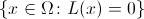
सबसे पहले, "भूलभुलैया" की बहुत अवधारणा पर निर्णय लेते हैं। भूलभुलैया से हमारा मतलब है एक बाइनरी फ़ंक्शन ऐसा क्षेत्र जुड़ा हुआ है। 0 का मान एक मुक्त सेल से मेल खाता है, और 1 का मान एक अभेद्य दीवार से मेल खाता है। कनेक्टिविटी की स्थिति बताती है कि किसी भी मुफ्त सेल से आप दीवारों को नष्ट किए बिना किसी अन्य को प्राप्त कर सकते हैं। समारोह हम फार्म में खोज करेंगे:

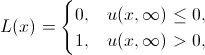
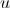
जहाँ - अमारी मॉडल का निर्णय। यह केवल मॉडल के मापदंडों को निर्धारित करने के लिए बनी हुई है।
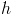
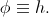
शुरू करने के लिए, हम एक मनमाना नकारात्मक मूल्य तय करते हैं । स्वाभाविक रूप से डाल दिया । अब हम फ़ंक्शन सेट करते हैं । प्रत्येक बिंदु पर इसका मान एक यादृच्छिक चर द्वारा समान रूप से एक खंड पर वितरित किया जाना चाहिए । इस मामले में, उत्तेजना गतिविधि नहीं बनाएगी। हम एक मनमाना सकारात्मक को ठीक करते हैं । यह पैरामीटर केवल संभावित के पूर्ण मूल्य को प्रभावित करता है, इसलिए यह ब्याज का नहीं है। हम मनमाना पॉजिटिव ठीक करते हैं । 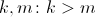वे भूलभुलैया की विशेषता दीवार की मोटाई निर्धारित करते हैं। पैरामीटर प्रयोगात्मक रूप से निर्धारित करने का प्रयास करें, और फिर पिछले अनुभाग में प्राप्त सैद्धांतिक अनुमान के साथ तुलना करें।
हम क्रमिक अनुमानों की विधि द्वारा एक स्थिर समाधान की तलाश करेंगे:

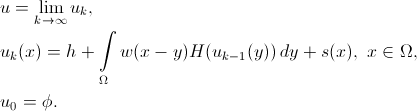
और यहाँ पाइथन में लंबे समय से प्रतीक्षित इंटरैक्टिव डेमो है:

import math import numpy import pygame from scipy.misc import imsave from scipy.ndimage.filters import gaussian_filter class AmariModel(object): def __init__(self, size): self.h = -0.1 self.k = 0.05 self.K = 0.125 self.m = 0.025 self.M = 0.065 self.stimulus = -self.h * numpy.random.random(size) self.activity = numpy.zeros(size) + self.h self.excitement = numpy.zeros(size) self.inhibition = numpy.zeros(size) def stimulate(self): self.activity[:, :] = self.activity > 0 sigma = 1 / math.sqrt(2 * self.k) gaussian_filter(self.activity, sigma, 0, self.excitement, "wrap") self.excitement *= self.K * math.pi / self.k sigma = 1 / math.sqrt(2 * self.m) gaussian_filter(self.activity, sigma, 0, self.inhibition, "wrap") self.inhibition *= self.M * math.pi / self.m self.activity[:, :] = self.h self.activity[:, :] += self.excitement self.activity[:, :] -= self.inhibition self.activity[:, :] += self.stimulus class AmariMazeGenerator(object): def __init__(self, size): self.model = AmariModel(size) pygame.init() self.display = pygame.display.set_mode(size, 0) pygame.display.set_caption("Amari Maze Generator") def run(self): pixels = pygame.surfarray.pixels3d(self.display) index = 0 running = True while running: self.model.stimulate() pixels[:, :, :] = (255 * (self.model.activity > 0))[:, :, None] pygame.display.flip() for event in pygame.event.get(): if event.type == pygame.QUIT: running = False elif event.type == pygame.KEYDOWN: if event.key == pygame.K_ESCAPE: running = False elif event.key == pygame.K_s: imsave("{0:04d}.png".format(index), pixels[:, :, 0]) index = index + 1 elif event.type == pygame.MOUSEBUTTONDOWN: position = pygame.mouse.get_pos() self.model.activity[position] = 1 pygame.quit() def main(): generator = AmariMazeGenerator((512, 512)) generator.run() if __name__ == "__main__": main() 

मुझे लगता है कि टिप्पणियां बहुत कम हैं। मैं केवल यह नोट करना चाहूंगा कि वजन फ़ंक्शन के साथ दृढ़ संकल्प की गणना गौसियन फ़िल्टर के माध्यम से की जाती है, और छवियां समय-समय पर पूरे विमान ("रैप" पैरामीटर) पर जारी रहती हैं। प्रदर्शन इस मायने में संवादात्मक है कि यह आपको क्लिक द्वारा किसी भी बिंदु पर एक सकारात्मक क्षमता को जबरन स्थापित करने की अनुमति देता है।
समाधान का व्यवहार, जैसा कि अपेक्षित था, पैरामीटर की पसंद पर निर्भर करता है :

अब हम पैरामीटर के इष्टतम मूल्य का एक सैद्धांतिक अनुमान प्राप्त करते हैं । यह शर्त को पूरा करता है:

इसलिए, यह अनुमान लगाया जा सकता है:

बुरा नहीं है, लेकिन वास्तविक अर्थ है सैद्धांतिक अनुमान से थोड़ा अधिक। इसे आसानी से सेट करके सत्यापित किया जा सकता है ।

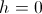
अंत में, आप पैरामीटर के मूल्य को बदलकर भूलभुलैया की "विरलता" की डिग्री बदल सकते हैं :

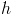
निष्कर्ष

इसलिए हमने चर्चा शुरू की, शायद, लेबिरिंथ पैदा करने के सबसे असाधारण तरीके से। मुझे उम्मीद है कि आपको लेख रोचक लगा होगा। अंत में, मैं उनके क्षितिज का विस्तार करने के इच्छुक लोगों के लिए संदर्भों की एक सूची प्रदान करूंगा:

[१] कोन्स्टेंटिन डब्रोविंस्की, डायनेमिक्स, स्टेबिलिटी एंड बिफुरकेशन फेनोमेना इन नोरलोकल मॉडल ऑफ़ कॉर्टिकल एक्टिविटी , २००५।
[२] दीवान जिन, डोंग लियांग, जिगन पेंग, अस्तित्व और गुणात्मक तंत्रिका क्षेत्र के स्थिर समाधान के गुण , २०११।
[३] स्टीफन कोम्बेस, हेल्मुट श्मिट, इंगो बोजैक, प्लानर न्यूरल फील्ड मॉडल्स में इंटरफ़ेस डायनेमिक्स , २०१२।