Coq के लिए नरम परिचय: रणनीति का उपयोग करना

सरलीकरण प्रमाण

इसलिए, पिछले भागों में हमने उनके ऊपर नए डेटा प्रकारों और कार्यों को परिभाषित किया। यह समय है कि कैसे अपने गुणों और व्यवहार को साबित करना और साबित करना है। एक अर्थ में, हम पहले से ही ऐसा करना शुरू कर चुके हैं - पहले भाग में हमने कीवर्ड Example का उपयोग करके एक प्रकार की इकाई परीक्षा लिखी थी, जिसमें एक विशिष्ट फ़ंक्शन के तर्कों पर लागू एक निश्चित फ़ंक्शन के व्यवहार के बारे में कुछ कथन शामिल थे। एक फ़ंक्शन की परिभाषा का उपयोग करते हुए, Coq अभिव्यक्ति को सरल करता है और समानता के लिए इसके बाएं और दाएं पक्षों की जांच करता है।

इस तरह के साक्ष्य का उपयोग कार्यों की एक विस्तृत श्रृंखला के लिए किया जा सकता है। हम दिखाते हैं कि 0 बाईं ओर के अतिरिक्त संचालन के लिए एक तटस्थ तत्व है:

 प्रमेय plus_O_n: forall n: nat, 0 + n = n।
 सबूत।
   simpl।  रिफ्लेक्सिविटी।  QED।

तुलना करने से पहले reflexivity कमांड स्पष्ट रूप से अभिव्यक्ति के दोनों पक्षों को सरल करता है।

कीवर्ड simpl और reflexivity , रणनीति के उदाहरण हैं। रणनीति का मुख्य लक्ष्य कोक को यह बताना है कि आवश्यक बयानों की शुद्धता को कैसे सत्यापित किया जाए। कार्यों की बजाय संकीर्ण सीमा है, जिसकी शुद्धता स्वचालित रूप से साबित की जा सकती है। आइए हम साबित करें कि 2 + 2 = 4:

 Coq <Lemma using_auto: 2 + 2 = 4
 1 सबजेल
  
   ============================
    2 + 2 = 4

 using_auto <प्रमाण।  ऑटो।  QED।

 प्रमाण पूरा हुआ।

 ऑटो।

 using_auto परिभाषित किया गया है

अधिकांश मामलों में, रणनीति का उपयोग करना आवश्यक है।

रणनीति intros

इकाई परीक्षणों के अलावा, जो तर्कों के एक सेट पर फ़ंक्शंस लागू करते हैं, हम उन कार्यक्रमों के गुणों को साबित करने में रुचि लेंगे जिनके निर्माण में गणितीय क्वांटिफायर हैं (उदाहरण के लिए, "सभी प्राकृतिक संख्याओं के लिए n ") और परिकल्पना (उदाहरण के लिए, " a = b ")। intros रणनीति intros मात्रात्मक और परिकल्पना को बयानों से वर्तमान तर्क के संदर्भ में स्थानांतरित करने की अनुमति देती है। आइए हम यह साबित करें कि किसी भी प्राकृतिक संख्या के बाएं गुणा का परिणाम शून्य है:

 प्रमेय बहु_रोजो: forall n: nat, 0 * n = 0।
 सबूत।  इंट्रो एन।  रिफ्लेक्सिविटी।  QED।

प्रमाण देना

एक और दिलचस्प उदाहरण पर विचार करें:

 प्रमेय plus_id_example: forall nm: nat,
 n = m ->
 n + m = m + n।

किसी भी n और m संबंध में एक सार्वभौमिक कथन तैयार करने और सिद्ध करने के बजाय, यह प्रमेय अधिक संकीर्ण गुणों की बात करता है जो n = m लिए धारण करते हैं। चूंकि n और m मनमानी संख्या हैं, इसलिए हम इसे साबित करने के लिए सरलीकरण का उपयोग नहीं कर सकते हैं। इसके बजाय, हम साबित करते हैं कि स्थिति में n साथ m को प्रतिस्थापित करना ( n = m मानते हुए), हमें सही पहचान मिलती है। कोक को इस तरह के बदलाव के लिए बताने वाली रणनीति को rewrite कहा जाता है:

 सबूत।
  intros n m।
  इंट्रो एच।
  फिर से लिखना -> एच।
  रिफ्लेक्सिविटी।  QED।

यहाँ क्या हुआ, इसे बेहतर ढंग से समझने के लिए, मैं अत्यधिक उदाहरण के लिए CoqIDE को चलाने और इस प्रमाण को एक-एक करके देखने की सलाह देता हूँ।

इसलिए, हम प्रमेय का वर्णन करते हैं और प्रमाण शुरू करते हैं:



अगला कदम सार्वभौमिक क्वांटिफायर और परिकल्पना से अभिव्यक्तियों को प्रमाण के वर्तमान संदर्भ में स्थानांतरित करना है (कोक्विड के ऊपरी दाहिने हिस्से में हम निरीक्षण करते हैं कि प्रमाण का वर्तमान संदर्भ कैसे बदलता है):



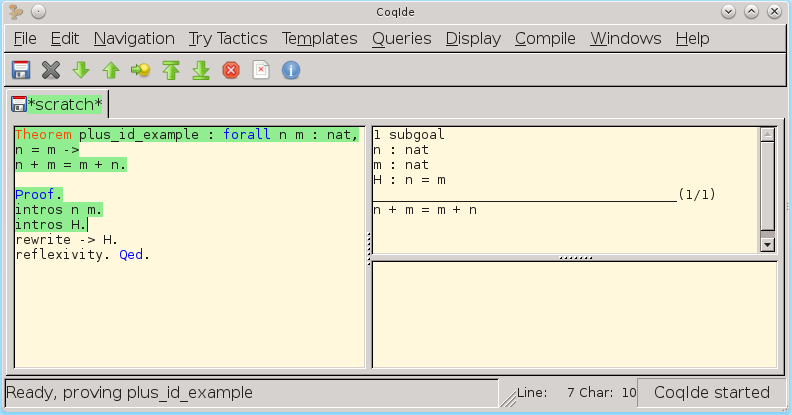
हम प्रमाण के वर्तमान उद्देश्य को फिर से लिखते हैं:



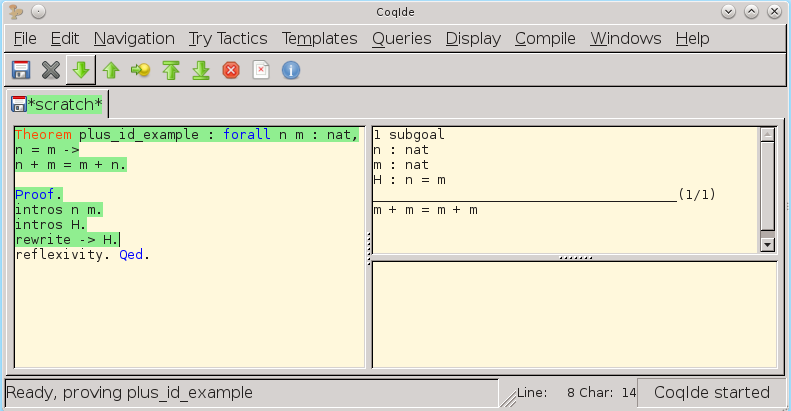
हम प्रमाण को सरल बनाकर समाप्त करते हैं:

निष्कर्ष

अगले भाग में, हम अधिक उन्नत युक्तियों को जानेंगे और Coq में डेटा संरचनाओं के साथ काम करना शुरू करेंगे। एक बार फिर, मैं पाठक का ध्यान कोकिदे में स्वतंत्र रूप से लॉन्च किए गए उदाहरणों के महत्व पर आकर्षित करता हूं।

पिछले भागों के लिंक:

1. प्रारंभ करें ।
2. प्रेरक परिभाषाएँ ।