एक छवि का आकार बदलने के लिए सीम नक्काशी एल्गोरिथ्म

सीम नक्काशी छवियों को आकार देने के लिए एक एल्गोरिथ्म है जो महत्वपूर्ण सामग्री को बचाता है और कम महत्वपूर्ण को हटा देता है। यह एस। एवदन और ए। शमीर के एक लेख में वर्णित किया गया है। यह छवि के सामान्य खिंचाव की तुलना में बेहतर परिणाम देता है क्योंकि यह छवि के महत्वपूर्ण तत्वों के अनुपात को नहीं बदलता है। नीचे दो तस्वीरें एल्गोरिथ्म के संचालन को प्रदर्शित करती हैं - मूल छवि का आकार 332x480 है, जबकि सीम नक्काशी'ओम 272x400 द्वारा संशोधित।


इस लेख में, मैं pseudocode और Matlab कोड का उपयोग करके एल्गोरिथ्म के संचालन का वर्णन करूंगा। अंग्रेजी में मेरे द्वारा लिखा गया मूल लेख यहाँ उपलब्ध है , जीथब पर स्रोत कोड।

छवि ऊर्जा

प्रस्तुति को सरल बनाने के लिए, मैं केवल छवि के आकार को कम करने के मामले का वर्णन करूंगा। एक तस्वीर बढ़ाना एक समान प्रक्रिया है।
एल्गोरिथ्म का विचार ऐसी सामग्री को हटाना है जो उपयोगकर्ता के लिए कम महत्व का हो (जिसमें कम जानकारी हो)। हम इस जानकारी को "ऊर्जा" का मापक कहेंगे। इस तरह के एक समारोह के रूप में, हम अंतरिक्ष l1 में छवि ढाल का उपयोग कर सकते हैं:
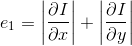
यदि तस्वीर में 3 चैनल हैं, तो पूरी छवि के ढाल के रूप में हम प्रत्येक चैनल के ग्रेडिएंट के योग का उपयोग करते हैं। नीचे दिया गया matlab कोड इस दृष्टिकोण को प्रदर्शित करता है:

function res = energyRGB(I) % returns energy of all pixelels % e = |dI/dx| + |dI/dy| res = energyGrey(I(:, :, 1)) + energyGrey(I(:, :, 2)) + energyGrey(I(:, :, 3)); end function res = energyGrey(I) % returns energy of all pixelels % e = |dI/dx| + |dI/dy| res = abs(imfilter(I, [-1,0,1], 'replicate')) + abs(imfilter(I, [-1;0;1], 'replicate')); end 

और यह प्रयोग की गई छवि को ऊर्जा फ़ंक्शन को लागू करने का परिणाम है:

सीवन

यदि हम एक न्यूनतम ऊर्जा लेकिन एक मनमाना स्थिति के साथ पिक्सेल निकालते हैं, तो छवि दूषित हो जाएगी। यदि हम न्यूनतम ऊर्जा वाले कॉलम / कॉलम हटाते हैं, तो अवांछित कलाकृतियां दिखाई देंगी। यहाँ, कॉलम से मेरा मतलब है {(i, j) | j तय है}, और कॉलम के तहत {(i, j) | मैंने तय किया}। दुविधा का समाधान स्तंभ / स्तंभ की अवधारणा के सामान्यीकरण को प्रस्तुत करना है।
औपचारिक रूप से, मैं एक nxm छवि हूं, फिर ऊर्ध्वाधर सीम को कॉल करें ।
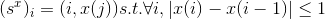
जहाँ x: [1, .., n] -> [1, .., m]। यही है, ऊर्ध्वाधर सीम छवि के ऊपर से नीचे तक का रास्ता है जैसे कि पथ की लंबाई छवि की चौड़ाई है, और सीम से संबंधित प्रत्येक तत्व (i, j) के लिए, अगला तत्व केवल (i + 1, j-1), (i) हो सकता है। +1, j), (i + 1, j +1)। इसी तरह, हम क्षैतिज सीम पेश कर सकते हैं। ऊर्ध्वाधर और क्षैतिज सीम के उदाहरण नीचे दिए गए हैं:


हम न्यूनतम ऊर्जा सीम में रुचि रखते हैं
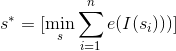
ऐसे सीम को खोजने के लिए, हम गतिशील प्रोग्रामिंग का उपयोग करते हैं:

1. प्रत्येक (i, j) के लिए सभी संभव सीमों के लिए न्यूनतम ऊर्जा का मैट्रिक्स M खोजना:
   
   • ऊर्जा मैट्रिक्स ई से मूल्यों के साथ पहली पंक्ति एम भरें
   • दूसरी से शुरू होने वाली सभी लाइनों के लिए:
     M [i, j] = e [i, j] + min (M [i - 1, j], M [i, j], M [i +1, j]);
   
   
2. मैट्रिक्स M की अंतिम पंक्ति में न्यूनतम मान ज्ञात करें और इस पिक्सेल से पहली पंक्ति तक एक पथ बनाएं, प्रत्येक चरण पर न्यूनतम ऊर्जा के साथ एक पिक्सेल चुनें (इसी तरह, (i, j), पदों में M के मूल्यों पर विचार करें [i - 1, j], [i] , j], [i + 1, j])।

दक्षता कारणों से, मैटलैब कोड में मैं nxm बिट मैट्रिक्स का उपयोग करके सीम का प्रतिनिधित्व करता हूं। यदि पिक्सेल सीम से संबंधित है, तो इसे 0 लेबल दिया गया है, अन्यथा 1।

 function [optSeamMask, seamEnergy] = findOptSeam(energy) % finds optimal seam % returns mask with 0 mean a pixel is in the seam % find M for vertical seams % for vertical - use I` M = padarray(energy, [0 1], realmax('double')); % to avoid handling border elements sz = size(M); for i = 2 : sz(1) for j = 2 : (sz(2) - 1) neighbors = [M(i - 1, j - 1) M(i - 1, j) M(i - 1, j + 1)]; M(i, j) = M(i, j) + min(neighbors); end end % find the min element in the last raw [val, indJ] = min(M(sz(1), :)); seamEnergy = val; optSeamMask = zeros(size(energy), 'uint8'); %go backward and save (i, j) for i = sz(1) : -1 : 2 %optSeam(i) = indJ - 1; optSeamMask(i, indJ - 1) = 1; % -1 because of padding on 1 element from left neighbors = [M(i - 1, indJ - 1) M(i - 1, indJ) M(i - 1, indJ + 1)]; [val, indIncr] = min(neighbors); seamEnergy = seamEnergy + val; indJ = indJ + (indIncr - 2); % (x - 2): [1,2]->[-1,1]] end optSeamMask(1, indJ - 1) = 1; % -1 because of padding on 1 element from left optSeamMask = ~optSeamMask; end 

क्षैतिज सीम को खोजने के लिए, ट्रांसपोज़्ड एनर्जी मैट्रिक्स को ढूंढने के लिए फ़ाइंडओप्सम फंक्शन को पास करें।

सबसे अच्छा तेजी हटाने के आदेश ढूँढना

तो, अब हम न्यूनतम सीम ढूंढ सकते हैं और नीचे दिए गए कोड का उपयोग करके हम इसे छवि से निकाल सकते हैं:

 function [optSeamMask, seamEnergy] = findOptSeam(energy) % finds optimal seam % returns mask with 0 mean a pixel is in the seam % find M for vertical seams % for vertical - use I` M = padarray(energy, [0 1], realmax('double')); % to avoid handling border elements sz = size(M); for i = 2 : sz(1) for j = 2 : (sz(2) - 1) neighbors = [M(i - 1, j - 1) M(i - 1, j) M(i - 1, j + 1)]; M(i, j) = M(i, j) + min(neighbors); end end % find the min element in the last raw [val, indJ] = min(M(sz(1), :)); seamEnergy = val; optSeamMask = zeros(size(energy), 'uint8'); %go backward and save (i, j) for i = sz(1) : -1 : 2 %optSeam(i) = indJ - 1; optSeamMask(i, indJ - 1) = 1; % -1 because of padding on 1 element from left neighbors = [M(i - 1, indJ - 1) M(i - 1, indJ) M(i - 1, indJ + 1)]; [val, indIncr] = min(neighbors); seamEnergy = seamEnergy + val; indJ = indJ + (indIncr - 2); % (x - 2): [1,2]->[-1,1]] end optSeamMask(1, indJ - 1) = 1; % -1 because of padding on 1 element from left optSeamMask = ~optSeamMask; end 

परिचालन का यह सेट पहले से ही छवि को चौड़ाई या ऊंचाई में आकार देने के लिए पर्याप्त है, जबकि महत्वपूर्ण विवरण बनाए रखते हैं - बस हटाएं कि कितने क्षैतिज और ऊर्ध्वाधर सीम की आवश्यकता है।
लेकिन क्या होगा अगर हमें एक साथ खड़ी और क्षैतिज रूप से छवि के आकार को कम करने की आवश्यकता है? प्रत्येक चलना पर कैसे समझें कि ऊर्जा को कम करने के मामले में क्या बेहतर है - ऊर्ध्वाधर सीम या क्षैतिज को हटाने के लिए?
डायनेमिक प्रोग्रामिंग का उपयोग करके इस समस्या को फिर से हल किया जा सकता है। आज्ञा देना n 'और m' वांछित छवि आकार है (n '<n, m' <m)। हम मैट्रिक्स टी का परिचय देते हैं, जो ऊर्ध्वाधर और क्षैतिज सीम को हटाने के इष्टतम अनुक्रम की लागत प्रत्येक n 'x m' के लिए निर्धारित करता है। सुविधा के लिए, हम आर = एन - एन ', एम = एम - एम' का परिचय देते हैं, जो ऊर्ध्वाधर और क्षैतिज हटाने की संख्या का वर्णन करता है। T के अलावा, हम आकार rxc का एक TBM मैट्रिक्स पेश करते हैं, जो कि प्रत्येक T (i, j) स्टोर 0 या 1 के लिए है, इस पर निर्भर करता है कि हम ऊर्ध्वाधर (1) या क्षैतिज (0) सीम को हटाकर T (i, j) में आए हैं या नहीं। छद्म कोड को नीचे दिखाया गया है:

1. टी (0, 0) = 0;
2. हम सीमा पर T के मान को प्रारंभिक करते हैं:
   सभी j के लिए {
   T (0, j) = T (0, j - 1) + E (सीमवर्टिकल);
   }
   सभी के लिए मैं {
   T (i, 0) = T (j - 1, 0) + E (सीम क्षैतिज);
   }
   
3. हम सीमा पर TBM मूल्यों को आरंभीकृत करते हैं:
   सभी j {T (0, j) = 1 के लिए; }
   सभी के लिए मैं {T (0, i) = 0; }
   
4. T और TBM भरें:
   i = 2 से r {के लिए
   imageWithoutRow = छवि;
   j = 2 से c {के लिए
   energy = computeEnergy (imageWithoutRow);
   
   हॉरिज़ेन्सेरएन्ज़ी = findHor क्षैतिजSeamEnergy (energy);
   verticalSeamEnergy = findVerticalSeamEnergy (ऊर्जा);
   tVertical = T (i - 1, j) + verticalSeamEnergy;
   tHor क्षैतिज = T (i, j - 1) _ क्षैतिजसमापन;
   अगर (tVertical <tHor क्षैतिज) {
   टी (i, j) = tVertical;
   transBitMask (i, j) = 1
   } {
   T (i, j) = t क्षैतिज;
   transBitMask (i, j) = 0
   }
   // बाएं से दाएं जाएं - ऊर्ध्वाधर सीम हटाएं
   imageWithoutRow = removeVerticalSeam (ऊर्जा);
   }
   
   energy = computeEnergy (छवि);
   image = removeHor क्षैतिजSeam (ऊर्जा);
   }
   
5. TBM (i, j) के मान के आधार पर एक पंक्ति या स्तंभ को हटाते हुए T (r, c) से T (1, 1) तक का मार्ग खोजें।

और मतलाब पर कार्यान्वयन:

 function [T, transBitMask] = findTransportMatrix(sizeReduction, image) % find optimal order of removing raws and columns T = zeros(sizeReduction(1) + 1, sizeReduction(2) + 1, 'double'); transBitMask = ones(size(T)) * -1; % fill in borders imageNoRow = image; for i = 2 : size(T, 1) energy = energyRGB(imageNoRow); [optSeamMask, seamEnergyRow] = findOptSeam(energy'); imageNoRow = reduceImageByMask(imageNoRow, optSeamMask, 0); transBitMask(i, 1) = 0; T(i, 1) = T(i - 1, 1) + seamEnergyRow; end; imageNoColumn = image; for j = 2 : size(T, 2) energy = energyRGB(imageNoColumn); [optSeamMask, seamEnergyColumn] = findOptSeam(energy); imageNoColumn = reduceImageByMask(imageNoColumn, optSeamMask, 1); transBitMask(1, j) = 1; T(1, j) = T(1, j - 1) + seamEnergyColumn; end; % on the borders, just remove one column and one row before proceeding energy = energyRGB(image); [optSeamMask, seamEnergyRow] = findOptSeam(energy'); image = reduceImageByMask(image, optSeamMask, 0); energy = energyRGB(image); [optSeamMask, seamEnergyColumn] = findOptSeam(energy); image = reduceImageByMask(image, optSeamMask, 1); % fill in internal part for i = 2 : size(T, 1) imageWithoutRow = image; % copy for deleting columns for j = 2 : size(T, 2) energy = energyRGB(imageWithoutRow); [optSeamMaskRow, seamEnergyRow] = findOptSeam(energy'); imageNoRow = reduceImageByMask(imageWithoutRow, optSeamMaskRow, 0); [optSeamMaskColumn, seamEnergyColumn] = findOptSeam(energy); imageNoColumn = reduceImageByMask(imageWithoutRow, optSeamMaskColumn, 1); neighbors = [(T(i - 1, j) + seamEnergyRow) (T(i, j - 1) + seamEnergyColumn)]; [val, ind] = min(neighbors); T(i, j) = val; transBitMask(i, j) = ind - 1; % move from left to right imageWithoutRow = imageNoColumn; end; energy = energyRGB(image); [optSeamMaskRow, seamEnergyRow] = findOptSeam(energy'); % move from top to bottom image = reduceImageByMask(image, optSeamMaskRow, 0); end; end 

निष्कर्ष

एल्गोरिथ्म परिदृश्य छवियों पर अच्छी तरह से काम करता है, जिफ को यह दिखाते हुए देखें कि एल्गोरिथम डायनेमिक्स में कैसे काम करता है (धन्यवाद के लिए):

लेकिन जैसा कि यह है, यह विवरणों से भरे चित्रों या चित्रों के लिए खराब रूप से अनुकूल है। परिदृश्य छवियों पर, आकाश या समुद्र में बहुत कम जानकारी होती है, और छवि, एक नियम के रूप में, उनके कारण कम हो जाती है। यदि हम बहुत सारे छोटे विवरणों के साथ एक छवि लेते हैं, तो एल्गोरिथ्म सबसे अच्छा परिणाम नहीं देगा (उदाहरण एवेडान और ए। शमीर द्वारा लेख से लिया गया है):

उपयोगकर्ता की भागीदारी के बिना, सीम नक्काशी को चित्र तस्वीरों पर लागू नहीं किया जाना चाहिए, क्योंकि हमारे लिए एक महत्वपूर्ण वस्तु - एक व्यक्ति - जिसमें सीम की नक्काशी के दृष्टिकोण से कम जानकारी है:

एल्गोरिथ्म का उपयोग छवि से चिह्नित वस्तुओं को हटाने के लिए किया जा सकता है (एक उदाहरण एवियन एंड ए शमीर लेख से लिया गया है):