एक बार मैंने एक खेल लिखने का फैसला किया। अपने लिए और अपने सुख के लिए। मुझसे पहले एक विकल्प था - सभी तैयार-किए गए उर्फ
Box2D का उपयोग करना या इसके लिए स्वयं भौतिकी लिखना। दूसरा विकल्प मुझे अधिक दिलचस्प लगा, और मैंने नेटवर्क की विशालता में जानकारी ढूंढना शुरू किया, जो मुझे मेरी ज़रूरत की हर चीज लिखने में मदद करेगा। खोज निकाला। नतीजतन, यह बहुत लचीला निकला (एक खेल के लिए) और एक साधारण शारीरिक इंजन। इंजन वेरलेट संख्यात्मक एकीकरण विधि पर आधारित था।

वर्लेट विधि समय में भौतिक बिंदुओं की गति का वर्णन करती है। इसके लिए अलग-अलग तरीके हैं। उदाहरण के लिए, समीकरणों की ऐसी प्रणाली।

2 समीकरणों को मिलाकर, हम प्राप्त करते हैं
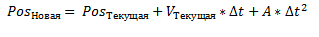
वर्लेट समीकरण उपरोक्त संकेतन से बहुत अलग नहीं है।

जैसा कि आप देख सकते हैं, वर्लेट विधि में, एक बिंदु की गति को उसके वर्तमान और पुराने समन्वय के बीच के अंतर के रूप में व्यक्त किया जाता है। खैर, हमें कम परेशानी है। इससे होने वाली गणना की सटीकता गिर रही है, लेकिन हम परमाणु रिएक्टरों की गिनती नहीं कर रहे हैं। प्लस यह टकराव की गणना को हास्यास्पद रूप से सरल बनाता है। एक उदाहरण का उपयोग करके बिंदु की गति पर विचार करें:
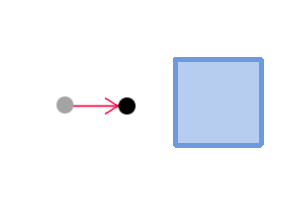
हम देखते हैं कि बिंदु के वर्तमान और पुराने निर्देशांक इस तरह से चुने गए हैं कि यह अनिवार्य रूप से नीले वर्ग की ओर दाईं ओर बढ़ता है। थोड़ा आगे बढ़ते हुए, मैं कहता हूं कि जब किसी वर्ग के साथ टकराव का पता चलता है, तो इस टकराव को संभालने के लिए, यह वर्ग के बिंदु के वर्तमान समन्वय को लाने के लिए पर्याप्त है। वह सब है। चूंकि यहां गति को निर्देशांक में अंतर के माध्यम से व्यक्त किया जाता है, वर्तमान या पुराने समन्वय में परिवर्तन स्वचालित रूप से बिंदु की गति में परिवर्तन की ओर जाता है।

यदि आप यह सब C ++ कोड में डालते हैं, तो आपको कुछ ऐसा मिलता है
struct Point { Vec2 Position; Vec2 OldPosition; Vec2 Acceleration; }; class Physics { int PointCount; Point* Points[ MAX_VERTICES ]; float Timestep; public: void UpdateVerlet(); }; void Physics::UpdateVerlet() { for( int I = 0; I < PointCount; I++ ) { Point& P = *Points[ I ]; Vec2 Temp = P.Position; P.Position += P.Position - P.OldPosition + P.Acceleration*Timestep*Timestep; P.OldPosition = Temp; } }
यह भौतिक बिंदुओं की गति का वर्णन करने के लिए पर्याप्त है। और यह अच्छा है यदि केवल अंक आपके खेल में योजनाबद्ध हैं। यदि आप कुछ और दिलचस्प चाहते हैं, तो आपको ठोस बनाने की आवश्यकता है। प्रकृति में, एक ठोस शरीर प्रकृति के रहस्यमय बलों द्वारा परस्पर कई परमाणु बिंदु हैं। काश, इस तरह की एक विधि एक खेल में भौतिकी का अनुकरण करने के लिए उपयुक्त नहीं है; कोई भी कंप्यूटर अरबों और अरबों अंकों की गणना और उनके बीच के कनेक्शन को नहीं खड़ा कर सकता है। इसलिए, हम भौतिक निकायों के कोने मॉडलिंग करके प्राप्त करेंगे। इस तरह से एक वर्ग के लिए 4 अंक और उनके बीच के कनेक्शन पर्याप्त होंगे। यह केवल इन कनेक्शनों का वर्णन करने के लिए रहता है। जाहिर है, कोने के बीच की दूरी स्थिर होनी चाहिए। यदि कोने के बीच की दूरी बदलती है, तो शरीर ख़राब हो जाएगा, लेकिन हम इसे नहीं चाहते हैं (जो लोग इसे अभी भी चुप हैं)। चोटियों के बीच की दूरी को स्थिर कैसे रखें? हकीकत में, इस समस्या को हल करने के लिए, लम्बाई के बीच उपयुक्त लंबाई का एक आर्मेचर डालना पर्याप्त होगा। आगे की हलचल के बिना, हम अपने सिमुलेशन में भी ऐसा ही करेंगे। आइए एक वर्ग बनाएं जो इस काल्पनिक सुदृढीकरण का वर्णन करेगा, आवश्यक दूरी पर कोने पकड़े हुए। एल्गोरिथ्म जो इस काम को करता है, उसे वर्टेक्स पॉइंट्स की गति को संसाधित करने के तुरंत बाद कहा जाएगा। संक्षेप में, यह बहुत सरल है। हम अपनी काल्पनिक सुदृढीकरण द्वारा जुड़े दो कोने के बीच वेक्टर की गणना करते हैं और इस वेक्टर की लंबाई की तुलना हमारी संदर्भ लंबाई के साथ करते हैं। यदि लंबाई अलग-अलग हैं, तो हम केवल आवृत्तियों को आवश्यक दूरी पर स्थानांतरित / धक्का दे सकते हैं, ताकि लंबाई फिर से मेल खाती हो और वॉयला हो - यह टोपी में है।
यह सब कोड में कैसा दिखता है:
struct Edge { Vertex* V1; Vertex* V2; float OriginalLength; }; void Physics::UpdateEdges() { for( int I = 0; I < EdgeCount; I++ ) { Edge& E = *Edges[ I ];
यहाँ यह है। यदि आप कई कोने बनाते हैं और उन्हें ऐसे पक्षों से एक साथ जोड़ते हैं, तो परिणामस्वरूप शरीर एक ठोस के गुणों को प्रदर्शित करेगा, जिसमें अन्य निकायों और फर्श के साथ टकराव के कारण रोटेशन शामिल है। यह सब कैसे काम करता है? आखिरकार, हमने बिंदुओं के बीच की दूरी को संरक्षित करने के लिए सिर्फ एक नया नियम जोड़ा, और यहां पर - तुरंत एक ठोस शरीर। यह रहस्य बहुत ही वेलेट इंटीग्रेशन विधि में निहित है। जैसा कि हम याद करते हैं, यह विधि गति से संचालित नहीं होती है, इसके बजाय, यह बिंदु की वर्तमान और पुरानी स्थिति के निर्देशांक के बीच के अंतर का उपयोग करती है। परिणामस्वरूप, गति में भी परिवर्तन होगा। और कोने के बीच एक निरंतर लंबाई बनाए रखने के लिए, हम बस उनके निर्देशांक बदलते हैं। चोटियों की गति में परिणामस्वरूप परिवर्तन एक ऐसा प्रभाव देता है जो लगभग ठोस पदार्थों के व्यवहार जैसा दिखता है। अधिक सटीक, लगभग ठोस। जिस रूप में कोड अब है, उसमें फर्श से टकराने और एक-दूसरे के खिलाफ होने पर शवों को विकृत किया जाएगा। क्यों? सब कुछ बहुत सरल है। यदि एक शीर्ष एक से अधिक साइड से जुड़ा हुआ है, और यह आमतौर पर होगा, तो एक पक्ष की लंबाई को समायोजित करने से स्वचालित रूप से दूसरे पक्ष की लंबाई में बदलाव होगा।
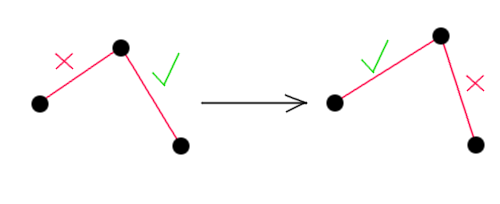
इस बीमारी का एकमात्र इलाज एक बहु कॉल फ़ंक्शन है, जो पक्षों की लंबाई को सही करता है। जितनी बार आप इसे बुलाएंगे, उतना ही सटीक अनुमान लगाया जाएगा। यह कितनी बार किया जाता है यह आपकी कल्पना पर निर्भर करता है। यह लेख का पहला भाग है। अगले भाग में, हम इस तरह के पहलुओं पर विचार करेंगे जैसे कि निकायों के बीच टकरावों का पता लगाना और प्रसंस्करण करना, साथ ही कानों के साथ कुछ झगड़े जो इस पद्धति का उपयोग करके किए जा सकते हैं।