डिजिटल सिग्नल सुचारू करना

परिचय

मुझे इस लेख को पोस्ट habrahabr.ru/post/183986 द्वारा लिखने के लिए मजबूर किया गया था, जहां छवि को चौरसाई करने के लिए कुछ एल्गोरिथ्म का सही उपयोग नहीं किया गया है।

चलिए बात तो सही है।

डिजिटल सिग्नल के गणितीय मॉडल - वैक्टर और मैट्रेस जिनके तत्व संख्या हैं। संख्याएं बाइनरी (बाइनरी सिग्नल), दशमलव ("सामान्य" सिग्नल) और इतने पर हो सकती हैं। किसी भी ध्वनि, किसी भी छवि और वीडियो को डिजिटल सिग्नल ^{1 में} परिवर्तित किया जा सकता है: वेक्टर में ध्वनि, मैट्रिक्स में छवि और वीडियो मैट्रिसेस के क्रमिक सेट में। इसलिए, एक डिजिटल सिग्नल है, एक कह सकता है, जानकारी प्रस्तुत करने के लिए एक सार्वभौमिक वस्तु।

चौरसाई कार्य वास्तव में, स्पस्मोडिक (चरण) से संकेत को फ़िल्टर करने का कार्य बदलता है। यह माना जाता है कि उपयोगी सिग्नल में उन्हें शामिल नहीं किया गया है। चरण-दर-चरण संकेत कई तेज, लेकिन आयाम में छोटे होने के कारण, स्तर की बूंदों में उच्च-आवृत्ति वाले घटक होते हैं जो स्मूथ सिग्नल में नहीं होते हैं। इसलिए, कुछ चौरसाई एल्गोरिथ्म के लिए, सबसे पहले, यह निर्धारित करना आवश्यक है कि विभिन्न आवृत्ति घटकों को बहुत अधिक कैसे देखा जाता है। दूसरे शब्दों में, संबंधित फिल्टर की आयाम-आवृत्ति विशेषता का निर्माण करना आवश्यक है, अन्यथा "कलाकृतियों" में चलने की उच्च संभावना है।

चौरसाई कार्य का उपयोग संकेतों को कम करते समय किया जा सकता है, अर्थात्, जब, उदाहरण के लिए, छोटे पर्दे पर एक बड़ी तस्वीर प्रदर्शित करना आवश्यक है। या जब ध्वनि की नमूना आवृत्ति घट जाती है, उदाहरण के लिए, 48000 हर्ट्ज से 44100 हर्ट्ज तक। सैंपलिंग फ़्रीक्वेंसी कम करना एक कपटपूर्ण ऑपरेशन है जिसके लिए प्रारंभिक सिग्नल प्रोसेसिंग (कम-पास फ़िल्टरिंग) की आवश्यकता होती है, लेकिन यह एक और चर्चा का विषय है ...

चलो "खराब" चौरसाई का एक उदाहरण देते हैं


ऐसा लगता है कि साधारण औसत और आउटपुट सिग्नल "सुचारू" होना चाहिए। लेकिन यह कैसे निर्धारित किया जाए कि वह कितना "चिकना" बने? क्या हम बहुत दूर चले गए हैं? या शायद कुछ कारकों को चुनने के लिए 1/3 नहीं? या शायद पाँच बिंदुओं पर औसतन? यह कैसे निर्धारित किया जाए कि सिग्नल में कितनी आवृत्ति घटक हैं? अपना इष्टतम कैसे खोजें (अर्थात किसी विशिष्ट कार्य के लिए)?
मैं इन और कुछ अन्य सवालों के जवाब देने की कोशिश करूंगा ताकि "साधारण" प्रोग्रामर अपने एल्गोरिथ्म को प्रमाणित कर सके, मुझे उम्मीद है कि न केवल "स्मूथिंग" के विषय पर एल्गोरिथ्म, जैसा कि विचारों को बहुत सामान्य रूप से प्रस्तुत किया जाएगा, जिससे आप खुद को सोचेंगे ...

संकेत

इस खंड में, एक संकेत एक वेक्टर है, जो कि एक निश्चित संख्या की संख्या का एक सरणी है। उदाहरण के लिए, चार तत्वों का एक वेक्टर = (2,5; 5; 0; -5)।

सरलता के लिए, केवल दशमलव वास्तविक संख्याओं पर विचार किया जाएगा।

सबसे आम और समझने योग्य संकेतों में से एक डिजीटल ध्वनि है। सिग्नल का आकार ध्वनि की अवधि और उस आवृत्ति पर निर्भर करता है जिसके साथ नमूने लिए जाते हैं (नमूना आवृत्ति पर)। एलिमेंट्स-सिग्नल नंबर डिवाइस के नमूने और स्टोरेज द्वारा मापी गई ध्वनि के वर्तमान आयाम पर निर्भर करते हैं।

जैसा कि पहले ही उल्लेख किया गया है, आसानी से बाहर निकालने का सबसे आसान तरीका है
(1)
जहां s मूल सिग्नल है, v स्मूथ सिग्नल है।

विधि (1) समन की सुचारू संपत्ति पर आधारित है, क्योंकि यह सभी के लिए स्पष्ट है कि कई यादृच्छिक संख्याओं के योग के रूप में परिकलित औसत मूल्य, संख्या की बढ़ती संख्या के साथ यादृच्छिक चर ^{2 की} तरह कम और कम हो जाता है, जो कि काफी सरल है, शोर ^{3 है} ।

लेकिन समीकरण (1) में गुणांक की पसंद का आधार क्या है? औसत की गणना किस पर की जाती है? ऐसा लगता है कि हाँ, लेकिन ... और अगर आप तीन शब्द नहीं ले रहे हैं, लेकिन सोलह और बत्तीस? .. केंद्रीय तत्व से नमूनों को अधिक से अधिक दूर क्यों करना चाहिए [i] समान वजन के साथ लिया जाना चाहिए? आखिरकार, यह पता चल सकता है कि नमूनों के बीच का कनेक्शन धीरे-धीरे उनके बीच की बढ़ती दूरी ⁴ से कमजोर हो जाएगा?

अगर हम पंक्ति में दस बार "तरबूज" शब्द के उच्चारण का एक उदाहरण मानते हैं और रिकॉर्ड किए गए सिग्नल के नमूनों के बीच संबंधों को ट्रैक करने का प्रयास करते हैं, तो हम अधिक से अधिक अलग-अलग नमूनों के बीच संबंधों के कमजोर पड़ने का पता लगा सकते हैं। स्वाभाविक रूप से, यदि हम "लंबी दूरी" पर विचार करते हैं, तो एक ही शब्द की पुनरावृत्ति के कारण ध्वनियों को दोहराया जाएगा और निर्भरता फिर से बढ़ जाएगी और गिर जाएगी, और इसी तरह। लेकिन, एक नियम के रूप में, वे चौरसाई करते समय "लंबी दूरी" पर विचार नहीं करते हैं, क्योंकि शोर व्यक्तिगत ध्वनियों के आसपास के क्षेत्र में दिखाई देते हैं, शब्द, वाक्यांश और वाक्य नहीं। शब्दों या यहां तक ​​कि वाक्यांशों के स्तर पर शोर स्पष्ट रूप से कृत्रिम (ध्वनि प्रभाव) या विदेशी प्राकृतिक (गूंज) है। यह पहले से ही "गैर-आयामी" शोर है, जिसके लिए एक अलग अध्ययन की आवश्यकता है। यहां हम "शुद्ध" शोर पर विचार करते हैं, जो सरल शब्दों में, कष्टप्रद शोर है और किसी भी उपयोगी संकेत की तरह बिल्कुल नहीं है।

सरल तर्क के आधार पर, यह स्पष्ट हो जाता है कि (1) (फिल्टर ऑर्डर) में शब्दों की संख्या इस बात पर निर्भर करती है कि पड़ोसी नमूने एक दूसरे पर कितनी बारीकी से निर्भर करते हैं। उदाहरण के लिए, तीसवां क्रम का एक फिल्टर लेने का कोई मतलब नहीं है, अगर एक के बाद एक केवल दस नमूनों की निर्भरता है। दरअसल, यह भी नहीं है कि "कोई मतलब नहीं है", लेकिन - यह असंभव है, क्योंकि यदि रीडिंग व्यावहारिक रूप से जुड़े नहीं हैं, तो उपयोगी सिग्नल का अत्यधिक चौरसाई शुरू हो जाएगा (सिलेबल्स का "खाना")। लेकिन यहां एक तीसरे क्रम का फ़िल्टर उपयोगी संकेत के बारे में जानकारी के उपयोग के संदर्भ में इष्टतम नहीं होगा, क्योंकि पहले से ही उल्लेख किया गया है, दस पड़ोसी नमूनों के क्रम की निर्भरता देखी गई है। इसलिए, आप प्रोसेसर के कंप्यूटर पर लोड को बढ़ाते हुए, नौवें क्रम के एक फिल्टर का उपयोग करके "अपनी किस्मत आजमा सकते हैं"। यहाँ यह पहले से ही निर्धारित करने के लिए आवश्यक है, सबसे अधिक संभावना है, लेकिन क्या यह खेल मोमबत्ती के लायक है?

कैसे अनुमान लगाया जाए कि आसन्न नमूने कितने निकट से संबंधित हैं? ऑटोकरेलेशन फ़ंक्शन (ACF) की गणना करें। जो लोग चाहते हैं, उन्हें विभिन्न शब्दों, वाक्यांशों, वाक्यांशों की पुनरावृत्ति और एसीएफ के बाद के निर्माण पर एक प्रयोग करने के लिए आमंत्रित किया जा सकता है (लाभ, उदाहरण के लिए, माटलब कार्यक्रम आपको कोड और सूत्रों के बारे में बहुत अधिक विचार किए बिना ऐसा करने की अनुमति देता है)।

तो आप (1) में फ़िल्टर गुणांक कैसे चुनते हैं?

इस मामले में, फ़िल्टर की प्रतिक्रिया को एक ही प्रभाव पर विचार करना सुविधाजनक है, अर्थात, प्रपत्र के संकेत के लिए


उदाहरण के लिए, फ़िल्टर (1) निम्नलिखित प्रतिक्रिया देगा (आवेग प्रतिक्रिया)

हम यह निष्कर्ष निकाल सकते हैं कि सिग्नल को सुचारू करने के बाद तीन तत्वों के बराबर हो गया। और यदि आप पांच तत्वों का एक फिल्टर लेते हैं? .. यह सही है, आउटपुट सिग्नल की अवधि पांच तत्वों के बराबर होगी। यह कितना उपयोगी है यह विशिष्ट स्थिति (कार्य) द्वारा निर्धारित किया जाता है।

वैसे, लंबे समय से प्रतीक्षित कलाकृति पहले से ही है! आवेग प्रतिक्रिया (1) अनिवार्य रूप से एक आयताकार आवेग है जो बिल्कुल भी चिकनी नहीं है! .. अजीब, सही? और अगर आप पांच-बिंदु फ़िल्टर लेते हैं? फिर आउटपुट पर हमें एक लंबा आयताकार नाड़ी मिलता है, लेकिन एक छोटे आयाम के साथ। यह बहुत अच्छी तरह से काम नहीं करता है ... सबसे सरल परीक्षण कहता है कि सरल औसत चौरसाई के लिए अनुपयुक्त है।

चलो आवृत्ति पक्ष से फ़िल्टर (1) को देखें (हमने पहले से ही अस्थायी रूप से देखा है)।

यदि संकेत ध्वनि है, तो यह हार्मोनिक सिग्नल ⁵ ("साइनसोइड्स") के एक सेट द्वारा काफी अच्छी तरह से वर्णित है और किसी विशेष साइनसॉइड के क्षीणन की डिग्री इसकी आवृत्ति पर निर्भर करती है। फिर से, एक चौरसाई फिल्टर के सही विकल्प के साथ, उपयोगी साइनसोइड्स में से कोई भी पूरी तरह से गायब नहीं होना चाहिए, अर्थात् , ऑपरेटिंग आवृत्ति रेंज में फिल्टर की आयाम-आवृत्ति विशेषता काफी समान होनी चाहिए।

आइए हम नमूने के प्रमेय की सीमा से परे, स्वाभाविक रूप से, एक निश्चित आवृत्ति के एक एकल-टोन सिग्नल पर विचार करें। बता दें कि समय का विवेकाधिकार चरण T _d एकता के बराबर है, अर्थात, नमूने एक सेकंड की वेतन वृद्धि में लिए जाते हैं। एक आवृत्ति f = 1 / (3 T _d ) = 1/3 हर्ट्ज के साथ एक संकेत लें, अर्थात


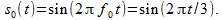
दो अवधि तक सीमित


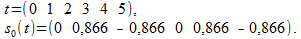
फ़िल्टर की प्रतिक्रिया (1) के बराबर होगी


अजीब तरह से, हम लगभग शून्य हो गए ... यह पता चला है कि आप उपयोगी सिग्नल के कुछ घटकों को खो सकते हैं।

थोड़ी उच्च आवृत्ति सिग्नल की प्रतिक्रिया की जांच करें


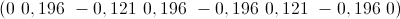
जैसा कि आप देख सकते हैं, तरंग खो नहीं है। क्या बात है? ।।

तथ्य यह है कि फिल्टर (1) की आयाम-आवृत्ति विशेषता कार्यशील आवृत्ति बैंड (शून्य से आधी नमूना आवृत्ति के लिए बैंड में) में मोनोटोनिक नहीं है और नमूना आवृत्ति की तुलना में तीन गुना कम आवृत्ति पर एक शून्य है। इसे कैसे दिखाया जाए?

सीधे शब्दों में कहें, एक फिल्टर की आवृत्ति प्रतिक्रिया निर्धारित करने के लिए, इनपुट पर स्पेक्ट्रम के लिए फिल्टर के आउटपुट पर स्पेक्ट्रम के अनुपात को खोजना आवश्यक है।

हम इनपुट s [ f ] के संकेत के स्पेक्ट्रम को S ( f ) के रूप में निरूपित करते हैं, फिर एक घड़ी चक्र T _d द्वारा संकेत s [ i -1] के स्पेक्ट्रम को मूल संकेत के स्पेक्ट्रम के माध्यम से व्यक्त किया जाता है।
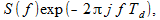
(2)
जहां j काल्पनिक इकाई है।

उन्नत सिग्नल s [ i +1] के स्पेक्ट्रम को व्यक्त किया जाता है
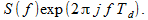
(3)

काल्पनिक इकाई का क्या अर्थ है? और कोई कैसे (2) और (3) को सही ठहरा सकता है?
यदि हम साइन, कोसाइन और एक्सपोनेंट के लिए प्रसिद्ध [1, 2] श्रृंखला लिखते हैं
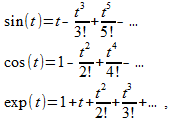
(4)
फिर एक नंबर j को चुनना जैसे कि j ² = -1, हम पहले दो के माध्यम से अंतिम पंक्ति व्यक्त कर सकते हैं
(5)
जिसका अर्थ है कि किसी भी जटिल संख्या को एक घातांक के माध्यम से काल्पनिक घातांक के माध्यम से लिखा जा सकता है। संख्या (5) का मॉड्यूल एक के बराबर है (काल्पनिक और वास्तविक भागों के वर्गों के योग का वर्गमूल), इसलिए, फॉर्म (5) में किसी भी जटिल संख्या को लिखने के लिए, इसे अपने मॉड्यूल से विभाजित और गुणा करना होगा
(6)

यह (5) और (6) से निम्नानुसार है कि यदि किसी काल्पनिक इकाई को कुछ वास्तविक संख्या से गुणा किया जा सकता है, तो उसे घातांक में अंतर किया जा सकता है, यह संख्या एक जटिल संख्या का तर्क है।

इस मामले में, संकेतों पर विचार किया जाता है, इसलिए, जटिल संख्या के आयाम मॉड्यूल हार्मोनिक सिग्नल के आयाम से मेल खाते हैं, और तर्क चरण है। यदि, उदाहरण के लिए, फॉर्म का संकेत लें
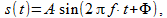
(7)
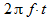
तब हम आयाम ए और चरण एफ को अलग कर सकते हैं। कारक - यह भी एक चरण है, और कुछ मामलों में इसे कोष्ठक से बाहर रखा गया है। उदाहरण के लिए, जब सिग्नल (7) कुछ फिल्टर से गुजरता है, तो इनपुट और आउटपुट पर संकेतों के चरण के अंतर को जानना महत्वपूर्ण है, जो फ़िल्टर किसी दिए गए आवृत्ति एफ पर परिचय देता है।

यदि संकेत ( ₀₎ t _{0 के} मान से देरी हो रही है, तो उसी संकेत को प्राप्त किया जाएगा, लेकिन एक निरंतर मान में चरण में स्थानांतरित कर दिया गया
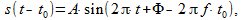
(8)
अर्थात्, जब एक मनमाना सिग्नल देरी हो जाता है, तो उसके सभी आवृत्ति घटकों को एक आवृत्ति द्वारा स्थानांतरित किया जाता है जो वर्तमान आवृत्ति और विलंब मूल्य पर निर्भर करता है। यह सूत्रों (2) और (3) की व्याख्या कर सकता है। इसलिए, किसी भी एल्गोरिथ्म का विश्लेषण करते समय, चरण-आवृत्ति विशेषता भी महत्वपूर्ण है, जो बताती है कि इनपुट सिग्नल के प्रत्येक आवृत्ति घटक फ़िल्टर (एल्गोरिथम) को कितनी देर तक रोकते हैं। कम और उच्च आवृत्तियों को आमतौर पर फ़िल्टर में एक अलग देरी होगी।

से (1), (2) और (3) यह इस प्रकार है कि फिल्टर की आवृत्ति प्रतिक्रिया (ट्रांसफर फ़ंक्शन) का रूप होगा
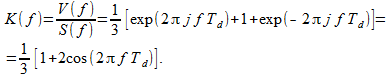
(9)

चूंकि आउटपुट सिग्नल के स्पेक्ट्रम को इनपुट के स्पेक्ट्रम के माध्यम से रैखिक रूप से व्यक्त किया जाता है, फिर जब आउटपुट (9), इनपुट सिग्नल का स्पेक्ट्रम सफलतापूर्वक कम हो जाता है। इसके अलावा, हम ध्यान दें कि फ़िल्टर की आवृत्ति प्रतिक्रिया (1) वास्तविक है, अर्थात, यह फ़िल्टर चरण विरूपण ^{6 का} परिचय नहीं देता है। हमने यह (सबसे अधिक संभावना है, अनजाने में) सूत्र की समरूपता के कारण हासिल किया (1): फ़िल्टर आउटपुट पर प्रत्येक नमूना वर्तमान और दो पड़ोसी नमूनों के योग के बराबर है।

शारीरिक रूप से, इस तरह के एक एल्गोरिथ्म को केवल भंडारण उपकरणों की उपस्थिति में लागू किया जाता है, क्योंकि यह प्रमुख नमूनों का उपयोग करता है (नमूना s [ i ] की गणना करने के लिए, नमूना s [ i +1] की आवश्यकता है)। यह वर्तमान में एक बड़ी समस्या नहीं है और, एक नियम के रूप में, वे सममित एल्गोरिदम का उपयोग करते हैं। यदि चरण विकृतियां उपयोगी साबित होती हैं, तो - कृपया, मुख्य बात यह है कि किसी भी एल्गोरिथ्म को जानबूझकर लागू करें और इसे विभिन्न कोणों से देखें: आवृत्ति और समय।

आवृत्ति पर (9) की निर्भरता की साजिश करना मुश्किल नहीं है। सरलीकृत करने के लिए, सामान्यीकृत आवृत्ति f ₀ = f T _{d को प्रस्तुत करें} , जिसमें से भिन्नता की उपयोगी सीमा [0 ... 0,5] है। नमूना प्रमेय के अनुसार आधे से अधिक नमूना आवृत्ति वाले आवृत्तियों के संकेत घटक अनुपस्थित होना चाहिए (डिजिटलीकरण से पहले, संकेत को निम्न कम-पास फिल्टर के माध्यम से पारित किया जाता है)। नमूनाकरण दर डिजिटल डिवाइस द्वारा प्रति सेकंड प्रेषित नमूनों की संख्या को इंगित करता है। यदि, उदाहरण के लिए, एक चक्र टी _डी एक मिलीसेकंड के बराबर है, तो एक सेकंड में एक हजार नमूने जारी किए जाने चाहिए।

विश्लेषण (9), यह ध्यान दिया जा सकता है कि, एक निश्चित अंतराल पर, संचरण गुणांक शून्य से कम है, और आयाम, परिभाषा के अनुसार, एक सकारात्मक मात्रा है ... स्थिति से बाहर का तरीका चरण विशेषता में माइनस साइन को हटाकर ट्रांसफर फ़ंक्शन मॉड्यूल का निर्माण करना है, जो, फिर भी, एक निरंतर नहीं है। (शून्य)। यदि हम संख्या "शून्य से एक" लेते हैं, तो इसे सूत्र (5) के रूप में दर्शाया जा सकता है
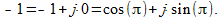
(10)
यह एक जटिल संख्या है जिसमें एक इकाई मॉड्यूल और 180 डिग्री (पीआई) का एक चरण है।

इस प्रकार, कुछ "उच्च" आवृत्तियों के लिए तीन-बिंदु सममित एल्गोरिथ्म (1) 180 डिग्री की एक चरण पारी का परिचय देता है, अर्थात यह केवल इनपुट सिग्नल को निष्क्रिय करता है। इस प्रभाव को 2/5 हर्ट्ज की सामान्यीकृत आवृत्ति पर ऊपर दी गई प्रतिक्रिया का विश्लेषण करके देखा जा सकता है।


अंजीर। 1. तीन-बिंदु सममितीय स्मूथिंग एल्गोरिथ्म के आयाम-आवृत्ति और चरण-आवृत्ति विशेषताएं (1)

अंजीर से। 1 यह तुरंत इस प्रकार है कि 1/3 की आवृत्ति के साथ एक संकेत इस एल्गोरिथ्म द्वारा दबा दिया जाएगा, और 1/3 से ऊपर की आवृत्ति वाले संकेतों को उलटा किया जाएगा। इस प्रकार, उपयोगी ऑपरेटिंग आवृत्ति रेंज को सुरक्षित रूप से [0 ... 0.5] से [0 ... 1/3] तक कम किया जा सकता है। यदि हम स्थानांतरण गुणांक में तेजी से गिरावट से संतुष्ट नहीं हैं, तो हमें एक और एल्गोरिथ्म निर्धारित करना होगा जिसमें एक अधिक आयताकार आयाम-आवृत्ति विशेषता है और साथ ही यह अभी भी अज्ञात है कि कौन सा चरण ...

वास्तव में, प्राप्त गैर-मोनोटोनिक आवृत्ति प्रतिक्रिया आवेग प्रतिक्रिया के आयताकार आकार का एक परिणाम है ..., 0, 0, ..., 1/3, 1/3, 1/3, 0, 0, ....। इसलिए, आवेग प्रतिक्रिया एल्गोरिदम में सकल खामियों को नोटिस करने का एक आसान तरीका है। आवृत्ति गणना, इसकी गणना की जटिलता के बावजूद, इसमें सुविधाजनक है कि यह आपको अधिक सूक्ष्म दोषों को नोटिस और खत्म करने की अनुमति देता है, जो हम करेंगे।

यदि हम अब एल्गोरिथ्म (1) को अधिक सामान्य रूप में लिखते हैं
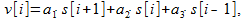
(11)
फिर, आवृत्ति प्रतिक्रिया के ज्ञान के आधार पर, आप गुणांक चुनने की कोशिश कर सकते हैं ताकि
ताकि आयाम-आवृत्ति विशेषता काम करने की आवृत्ति रेंज में मोनोटोनिक हो जाए (0 ... 0.5)। इसके लिए, कम से कम, ऑपरेटिंग रेंज के भीतर शून्य का अभाव आवश्यक है।

चूँकि हमारे पास विलंबित नमूना s [i - 1] को प्रतिष्ठित s [i + 1] के संबंध में अलग करने का कोई कारण नहीं है, हम गुणांक ₁ और _{3 को} समान करते हैं। हम संचरण गुणांक लिखने के बाद
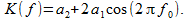
(12)

आइए पहले शून्य को आवृत्ति f ₀ = 0.5 पर ले जाने का प्रयास करें। इसके लिए, एक ₂ = 2 ए ₁ की समानता को पूरा किया जाना चाहिए, अर्थात, साइड नमूनों का वजन केंद्रीय एक का आधा वजन होना चाहिए। तब एक अधिक इष्टतम एल्गोरिदम इस तरह दिखाई देगा
(13)

कैसे (13) एक एकल गुणांक ₁ चुनने के लिए?

आइए हम पल्स क्षणिक प्रतिक्रिया के दृष्टिकोण से एल्गोरिथ्म (13) पर एक नज़र डालें। ऐसा करने के लिए, एकल कूद की प्रतिक्रिया ढूंढें :
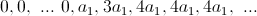
(14)

जैसा कि हम देखते हैं, एकता के बराबर स्थिर स्थिति में आउटपुट आयाम बनाए रखने के लिए, गुणांक ₁ = 1/4 चुनना आवश्यक है। यही है, सभी गुणांक का योग एक के बराबर होना चाहिए।

अंत में, समाप्त एल्गोरिथ्म के लिए
(16)
यह (छवि 2) आवृत्ति विशेषताओं का निर्माण करना संभव है: आयाम और चरण।


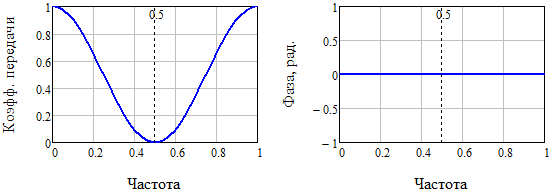अंजीर। 2. तीन-बिंदु सममितीय स्मूथिंग एल्गोरिथ्म की आयाम-आवृत्ति और चरण-आवृत्ति विशेषताएं (16)

विश्लेषण चित्र। 2 दिखाता है कि चरण विकृतियां गायब हो गई हैं, और आयाम विशेषता कार्यशील आवृत्ति बैंड [0 ... 0.5] में एकरस बन गई है। एक मायने में, हमने तीन-बिंदु फ़िल्टर से सब कुछ निचोड़ लिया।

अब यह स्पष्ट हो जाता है कि सरल औसत हमेशा इष्टतम से बहुत दूर है, खासकर जब औसत नमूने बहुत होते हैं।

छवि

छवियों के लिए, कुछ हद तक संकेतों के लिए सब कुछ समान है: आयाम और चरण विकृतियां, आवेग प्रतिक्रियाएं, सिग्नल ऊर्जा - मुख्य अंतर यह है कि वैक्टर के बजाय मैट्रिस का उपयोग किया जाता है। यह भी ध्यान दिया जाना चाहिए कि छवियों के लिए समय समन्वय नहीं है, लेकिन अंतरिक्ष का एक समन्वय है, इसलिए स्थानिक नमूना आवृत्तियों हैं। यह अंतर बल्कि औपचारिक है, क्योंकि यह एल्गोरिदम के गणित को बिल्कुल प्रभावित नहीं करता है।

अब पड़ोसी बिंदुओं (छवि 3) द्वारा छवि को चौरसाई करने के लिए "सबसे सरल" एल्गोरिथ्म पर विचार करें। फ़िल्टर आउटपुट पर v _{00 की} गणना करें
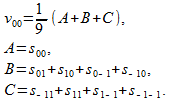
(17)


अंजीर। 3. पड़ोसी बिंदुओं पर छवि को सुचारू करने की योजना

सूत्र (17) में, तीन पद A , B, और C को विशेष रूप से प्रतिष्ठित किया गया है, क्योंकि B और C में चार समान आंतरिक शब्दों की केंद्रीय संदर्भ s ₀₀ से अपनी दूरी है। यहां यह मानना ​​स्वाभाविक है कि ए शब्द का अधिकतम वजन होगा, फिर बी और सी अवरोही क्रम में।

छवियों के लिए, स्पेक्ट्रम और ट्रांसमिशन गुणांक दो-आयामी होगा, अर्थात्, वे दो आवृत्तियों पर निर्भर करेंगे: पहली आवृत्ति क्षैतिज है, दूसरी ऊर्ध्वाधर है (सब कुछ सशर्त है, निश्चितता के लिए)।

फ़िल्टर (17) में निम्न संचरण गुणांक है
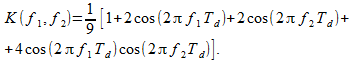
(18)

यदि हम उदाहरण के लिए, लगभग तीस असतत आवृत्तियों और निर्माण (छवि 4) आवृत्ति प्रतिक्रिया मॉड्यूल (18) का एक समोच्च ग्राफ बनाते हैं, तो हम अंजीर में उन लोगों के समान विकृतियों को देख सकते हैं। 1. निचले बाएँ कोने सबसे कम आवृत्तियों से मेल खाती है। आवृत्तियों पर आवृत्ति प्रतिक्रिया में एक डुबकी है जो नमूना आवृत्ति का 1/3 है (इस मामले में नमूना आवृत्तियों दोनों निर्देशांक में 64 हैं)।


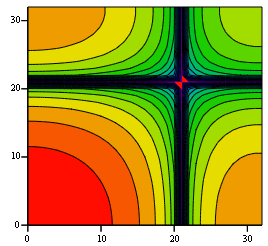अंजीर। 4. नौ-बिंदु सममित स्मूथी एल्गोरिथ्म (17) के आयाम-आवृत्ति विशेषता

अंजीर में नमूनों के लिए गुणांक फेरबदल। 3, आप निम्नलिखित चौरसाई एल्गोरिथ्म प्राप्त कर सकते हैं
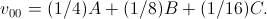
(19)

इसके अलावा, यदि छवि के केंद्र में एक भी एक्सपोज़र रखा जाता है, तो फ़िल्टर (19) की प्रतिक्रिया का रूप होगा
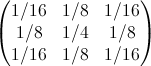
(20)

वास्तव में, (20) फिल्टर की आवेग प्रतिक्रिया है (ये नौ मुख्य मायने हैं, क्योंकि बाकी शून्य हैं)। आवेग प्रतिक्रिया के सभी नमूनों का योग एक के बराबर है। फ़िल्टर की आवृत्ति प्रतिक्रिया (19) में अंजीर में दिखाया गया रूप है। 5।


अंजीर। 5. एक नौ-बिंदु सममित स्मूथी एल्गोरिथ्म की आवृत्ति प्रतिक्रिया (19)

फिर से हम देखते हैं (छवि 4 और छवि 5 की तुलना करें) एल्गोरिदम की सामान्य औसत में सुधार।

सारांश

डिजिटल सिग्नल (चौरसाई और अधिक) के प्रसंस्करण के लिए एल्गोरिदम विकसित करते समय, आपको सरल औसत जैसे सहज ज्ञान युक्त एल्गोरिदम पर भरोसा नहीं करना चाहिए।

अधिक सामान्य दृष्टिकोण भारित योग की तकनीक है (केवल रैखिक एल्गोरिदम पर विचार किया गया था जब नमूने केवल स्थिरांक से गुणा किए जाते हैं, और परिणाम जोड़े जाते हैं)।

वेट समन, जब कम वज़न को केंद्रीय तत्व से दूर रखा जाता है, तो दोनों सांख्यिकीय रूप से उचित है (बढ़ती दूरी के साथ निर्भरता के कमजोर होने की प्राकृतिक प्रकृति) और कार्यात्मक रूप से (यह गुणांक का चयन सख्ती से मज़बूती से करना संभव है, आयाम-आवृत्ति विशेषता की एकरसता सुनिश्चित करना)।

फ़िल्टर की आयाम-आवृत्ति विशेषताओं द्वारा एक बड़ी भूमिका निभाई जाती है, जो भारित योग के गुणांक द्वारा निर्धारित की जाती है। वे आपको यह साबित करने की अनुमति देते हैं कि एक दिया गया फिल्टर एक निश्चित आवृत्ति सीमा को पार करता है और दूसरे को अवरुद्ध करता है। इसके अलावा, बाधा में और इतने पर, पासबैंड में असमानता का निर्धारण करना संभव है। फ़िल्टर का क्रम जितना अधिक होगा, स्वतंत्रता की उतनी अधिक डिग्री और आयाम-आवृत्ति विशेषता के आकार को चुनना बेहतर होगा।

एक महत्वपूर्ण भूमिका भी चरण-आवृत्ति विशेषताओं द्वारा निभाई जाती है, जो मुख्य रूप से एल्गोरिथम के समरूपता की डिग्री द्वारा निर्धारित की जाती है। वास्तविक समय के एल्गोरिदम, जब पहली उलटी गिनती के आगमन के क्षण में एक उलटी गिनती फ़िल्टर के आउटपुट पर दिखाई देती है, तो वे समरूप चरण प्रतिक्रिया नहीं दे सकते हैं (निरंतर, सबसे अधिक बार "शून्य"), क्योंकि वे सममित नहीं हो सकते। इस तरह के एल्गोरिदम इनपुट सिग्नल में देरी का परिचय देते हैं: उदाहरण के लिए, एक चिकनी छवि आमतौर पर दोनों निर्देशांक में स्थानांतरित हो सकती है। यदि छवि जटिल है (अर्थात, इसमें कई आवृत्ति घटक हैं), तो चरण विकृतियां इसे विशेष रूप से विकृत कर सकती हैं, और न केवल इसे निर्देशांक में स्थानांतरित कर सकती हैं, जो सरल छवियों के लिए लगभग सच है।

आपको एक निश्चित एल्गोरिथ्म के अनुरूप फ़िल्टर के आवेग प्रतिक्रिया पर भी ध्यान देना चाहिए। यह सीधे फिल्टर के संचालन को देखने का एक सरल तरीका है, जो संकेत के लिए समय के पैमाने पर या छवि के लिए स्थानिक निर्देशांक के पैमाने में अनुमति देता है।

और अंत में, संबंधित फ़िल्टर के आउटपुट पर सिग्नल हानि को निर्धारित करने के लिए एल्गोरिथ्म के एक ऊर्जा विश्लेषण की आवश्यकता होती है। यह विश्लेषण पल्स क्षणिक प्रतिक्रिया के ढांचे में आसानी से किया जाता है।

फ़ुटनोट

1. हमेशा नुकसान के साथ, चूंकि ऑपरेशन की आवृत्ति और डिजिटल उपकरणों की क्षमता सीमित होती है
2. औसत मूल्य की स्थिर संपत्ति सही है यदि यादृच्छिक संख्या जनरेटर की विशेषताएं अपरिवर्तित हैं, अर्थात्, आदर्श रूप से, जनरेटर को किसी दिए गए वितरण कानून के साथ यादृच्छिक मूल्य देना चाहिए
3. यदि, निश्चित रूप से, देखा गया शोर। - यह एक एन्क्रिप्टेड उपयोगी संकेत नहीं है, जो उन लोगों के लिए यादृच्छिक हो जाता है जिनके पास कुंजी नहीं है ...
4. एक ऑडियो सिग्नल के लिए, नमूनों के बीच की दूरी एक निश्चित अवधि
5 है। हम मान सकते हैं कि कोई भी संकेत को कई आवृत्तियों के साइनसोइड्स के योग के रूप में दर्शाया जा सकता है, लेकिन ध्वनि संकेत को आवृत्तियों की एक श्रृंखला में "अच्छी तरह से" होना चाहिए
6. इसे कहने के लिए सरल किया जा सकता है, पाठ में नीचे दिए गए विवरण देखें

सूत्रों का कहना है

1. त्रिकोणमितीय कार्य [इलेक्ट्रॉनिक संसाधन], पहुंच मोड: नि: शुल्क, en.wikipedia.org/wiki/%D2%F0%E8%E3%EE%ED%EE%EC%E5%F2%F2%F8%F7%F7%E5 % F1% EA% E8% E5_% F4% F3% ED% EA% F6% E8% E8
2. प्रदर्शक [इलेक्ट्रॉनिक संसाधन], पहुंच मोड: नि: शुल्क, en.wikipedia.org/wiki/%DDHEA%F1% EF% EE% ED% E5% ED% F2% E0