🕕 🍏 👩🏻‍🤝‍👨🏾 छिपे हुए मार्कोव चेन, बॉम-वेल्श एल्गोरिथ्म 🎴 🔦 🥣

छिपे हुए मार्कोव मॉडल / चेन डेटा पेश करने के कुछ दृष्टिकोण हैं। मुझे वास्तव में पसंद आया कि इस लेख में इनमें से कितने दृष्टिकोण संक्षेप में प्रस्तुत किए गए हैं।

छिपे हुए मार्कोव मॉडल का वर्णन करने वाले अपने पिछले लेख की निरंतरता में, मैं खुद से पूछता हूं: एक अच्छा मॉडल कहां प्राप्त करें? उत्तर काफी मानक है, एक अच्छा मॉडल लें और उसमें से एक अच्छा बनाएं।

मैं आपको एक उदाहरण याद दिलाता हूं: हमें एक झूठ डिटेक्टर को लागू करने की आवश्यकता है, जो किसी व्यक्ति के हाथों को हिलाकर निर्धारित करता है कि वह सच कह रहा है या नहीं। माना कि जब कोई व्यक्ति झूठ बोलता है, तो उसके हाथ थोड़ा और हिलते हैं, लेकिन हम नहीं जानते कि वास्तव में कितना सही है। आइए यादृच्छिक पर मॉडल लें, पिछले लेख से विटर्बी एल्गोरिथ्म चलाएं और बहुत अजीब परिणाम प्राप्त करें:

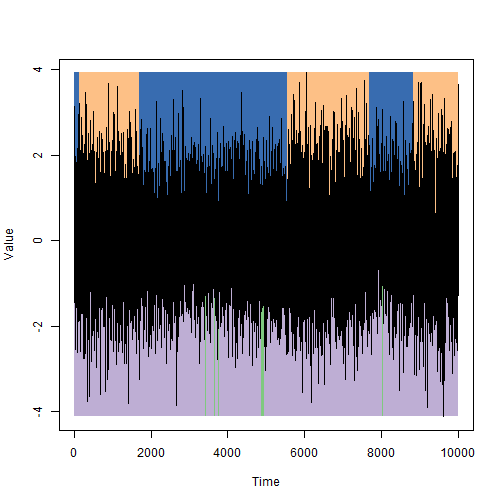
परिणामी विभाजन में कोई अर्थ नहीं है; अधिक सटीक, वहाँ है, लेकिन ऐसा नहीं है जिसे मैं देखना चाहूंगा। पहला प्रश्न: चयनित मॉडल में मौजूदा नमूने की उपस्थिति की संभावना का आकलन कैसे करें। और दूसरा सवाल यह है कि एक मॉडल कैसे खोजना है जिसमें मौजूदा नमूना सबसे प्रशंसनीय होगा, अर्थात गुणवत्ता का मूल्यांकन कैसे करें और नए डेटा के लिए अनुकूलन क्षमता कैसे व्यवस्थित करें। यह उनके लिए है कि आगे-पीछे की प्रक्रिया और बॉम-वेल्च पुनर्संयोजन प्रक्रिया का जवाब है।

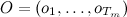
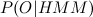
आगे-पीछे की प्रक्रिया आपको इस संभावना का मूल्यांकन करने की अनुमति देती है कि इस एचएमएम मॉडल में मनाया मूल्यों का एक नमूना दिखाई देगा। $O = (o_1, \ ldots, o_ {T_m})$ (पिछले लेख से लिए गए पदनाम)। मूल्यांकन समारोह को इस रूप में निरूपित करें P (O | HMM)

। और हम दो अतिरिक्त कार्य करते हैं:

AlphaFunc<-function(S,I,T,P,O,Tm) { la<-I*Es(P,O[1]) alpha<-cbind(la) for(t in 2:Tm) { la<-as.vector((la*Es(P,O[t]))%*%T) alpha<-cbind(alpha,la) } return (alpha) } BetaFunc<-function(S,I,T,P,O,Tm) { lb<-rep(1,length(S)) beta<-cbind(lb) for(t in Tm:2) { lb<-as.vector(T%*%(Es(P,O[t])*lb)) beta<-cbind(lb, beta) } return (beta) }

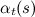
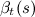
कार्यों $\ Alpha_t (s)$ । $\ Beta_t (s)$ निम्नलिखित दिलचस्प गुण हैं:

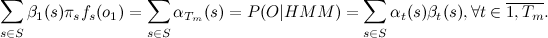
$\ __ \ _ \ _ में S} \ बीटा_1 (s) \ pi_s f_s (O_1) = \ sum_ {s \ _ S} \ \ _ अल्फा_ {T_m} (s) = P (O | HMM) \ _ \ _ \ _ \ _ S} \ Alpha_t (s) \ Beta_t (s), \ forall t \ in \ overline {1, T_t}।$
इसलिए, हम पहले से ही जानते हैं कि एचएमएम मॉडल में ओ नमूने की उपस्थिति का मूल्यांकन कैसे करें और छिपे हुए राज्यों के अनुक्रम का पता लगाएं क्यू ^ *

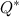
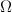
। खुला सवाल बना हुआ है, कैसे एक मॉडल को खोजने के लिए जिसमें मौजूदा नमूने की उपस्थिति की संभावना अधिकतम होगी, अर्थात $P (O | HMM ^ *) = \ max \ limit_ {HMM \ in \ Omega} P (O | HMM) |$ जहाँ $\ _ ओमेगा$ वैध मॉडल के कुछ सेट। कथित तौर पर, इष्टतम खोजने के लिए कोई औपचारिक एल्गोरिथ्म नहीं है, लेकिन मॉडल के कुछ संशोधन के कारण, कम से कम "पूर्णता" के करीब थोड़ा कम करना संभव है। यह है कि कैसे पुनरावृत्त EM एल्गोरिदम काम करते हैं ।

तो चलो एक प्रारंभिक मॉडल है हम्म ^ के

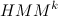
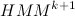
इस तरह के एक मॉडल को खोजने की जरूरत है $HMM ^ {k + 1}$ कि $P (O | HMM ^ {k + 1}) \ geq P (O | HMM ^ {k})$ । चलिए शुरू करते हैं।

हम दो और सहायक कार्यों का परिचय देते हैं:

 xiGamma<-function(t,alpha,beta,S,T,P,O) { xi<-matrix(0,nrow=length(S),ncol=length(S)) denom<-alpha[,t]%*%beta[,t] for(sin in S) { for(sout in S) { nom<-alpha[sin,t]*T[sin,sout]*Es(P,O[t+1])[sout]*beta[sout,t+1] xi[sin,sout]<-nom/denom } } return(list(xi=xi,g=rowSums(xi))) } XiGammas<-function(Tm,alpha,beta,S,T,P,O) { xis<-c() gs<-c() for(t in 1:(Tm-1)) { xg<-xiGamma(t,alpha,beta,S,T,P,O) xis<-cbind(xis,as.vector(xg$xi)) gs<-cbind(gs,as.vector(xg$g)) } return(list(xi=xis,g=gs)) }

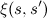
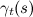
$\ xi (s, s ')$ समय-समय पर राज्य s से राज्य s तक के परिवर्तनों के अंश के रूप में व्याख्या की जाती है $\ gamma_t (s)$ - समय पर राज्य से संक्रमणों के कुल अंश के रूप में टी।

मॉडल के मापदंडों को ठीक किया $HMM ^ {k + 1} = \ langle M ^ {k + 1}, S ^ {k + 1}, I ^ {k + 1}, T ^ {k + 1}, E ^ {k + 1} \ _ rangle$ निम्न रूप होगा:

 BaumWelshFunc<-function(S,I,T,P,O,Tm) { a<-alphaLog(S,I,T,P,O,Tm) b<-betaLog(S,I,T,P,O,Tm) xg<-XiGammas(Tm, a,b, S,T,P,O) xi<-rowSums(xg$xi) dim(xi)<-c(length(S),length(S)) g<-rowSums(xi) new_I <- g/sum(g) small_t<-rep(g,length(S)) dim(small_t)<-c(length(S),length(S)) new_T <- xi/small_t norm_params<-NormalReestimation(xg$g,O[1:(Tm-1)],S) new_P<-c() for(s in S) { new_P<-c(new_P,Curry("dnorm",mean=norm_params$mu[s], sd=sqrt(norm_params$sigma2[s]))) } return(list(S=S,I=new_I,T=new_T,P=new_P,N=norm_params)) }

फ़ंक्शन रीसेट करें f_s (ओ)

(हमारे मामले में NormalReestimation) विशिष्ट स्थिति पर निर्भर करता है। एल्गोरिथ्म का शास्त्रीय कार्यान्वयन मानता है कि टिप्पणियों को असतत असतत वितरण द्वारा वर्णित किया गया है, जो हमारे लिए उपयुक्त नहीं है। प्रेक्षित मानों के लिए मानकों का आकलन करने के लिए निम्नलिखित विधि का उपयोग करना प्रस्तावित है

 NormalReestimation<-function(g,O,S) { denom<-rowSums(g) mu<-g%*%O/denom sigma2<-c() for(s in S) { s2<-g[s,]%*%(O-mu[s])^2 sigma2<-c(sigma2,s2) } return(list(mu=as.vector(mu),sigma2=sigma2/denom)) }

अधिक सामान्य तरीके से झूठ डिटेक्टर समस्या पर विचार करें। हमारे पास एक सामान्य मॉडल है कि कैसे हमारा झूठ डिटेक्टर विषयों के झूठ और ईमानदारी पर प्रतिक्रिया करता है और एक विशिष्ट व्यक्ति है जो कभी-कभी झूठ और कभी-कभी सच कहता है। हम इस विशेष व्यक्ति के साथ काम करने के लिए अपने मॉडल को अनुकूलित करना चाहते हैं।

दिए गए:

मॉडल। दो छिपे हुए राज्य हैं जब एक गोलाकार व्यक्ति सच कह रहा है और जब वह झूठ बोल रहा है। दोनों मामलों में, हाथों की चिकोटी को सफेद शोर के रूप में दर्शाया जा सकता है, लेकिन फैलाव
हमारे व्यक्ति के लगातार 10,000 टिप्पणियों का एक नमूना।

यह आवश्यक है:

इस व्यक्ति की ईमानदारी / झूठ के मामले में हाथ के झटके के विचरण का आकलन करें।
उसके लिए इन राज्यों के परिवर्तन के क्षणों का निर्धारण करें।

समाधान:

चलो हमारे पाँच सेट करें:
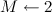1. राज्यों की संख्या $M \ leftarrow 2$ ;
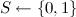2. राज्यों $S \ leftarrow \ {0,1 \}$ ;
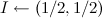3. प्रारंभिक वितरण $I \ leftarrow (1 / 2,1 / 2)$ ;
4. डिफ़ॉल्ट रूप से, मान लीजिए कि राज्य समान हैं और कहते हैं कि परिवर्तन प्रत्येक 999 घड़ी चक्र पर एक बार औसतन होता है:
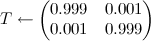  $T \ leftarrow \ left (\ start {मैट्रिक्स} 0.999 और 0.001 \\ 0.001 और 0.999 \ end {मैट्रिक्स} \\)$ ;
5. $E = (N (0,1 / 2 \ cdot \ sigma ^ 2), N (0,2 \ cdot \ sigma ^ 2))$ जहाँ $\ sigma ^ 2 = var (X)$ ।
  मैं समझा दूंगा पूरे नमूने के लिए नमूना विचरण है। प्रारंभिक मूल्यांकन कार्य इस तरह से चुना जाता है कि पहला राज्य कम फैलाव मानों से मेल खाता है, और दूसरा बड़े लोगों के लिए। यह महत्वपूर्ण है कि वे अलग हैं।
हम मूल्यांकन समारोह के मूल्य को स्थिर होने तक बॉम-वेल्श एल्गोरिथ्म का उपयोग करके मापदंडों को फिर से कॉन्फ़िगर करेंगे।
हम Viterbi एल्गोरिथ्म का उपयोग करते हुए समय में प्रत्येक क्षण के लिए सबसे अधिक छिपी हुई स्थिति पाएंगे।

हम पहली तस्वीर से डेटा पर उत्तर का वर्णन करते हैं: राज्य के शीर्ष पर, जैसा कि वे सिमुलेशन के दौरान राज्य के तल पर सेट किए गए थे, जिन्हें छिपे हुए मार्कोव श्रृंखला विधि का उपयोग करके चुना गया था।

नीचे दिए गए ग्राफ़ पर हम बॉम-वेल्श एल्गोरिथम की पुनरावृत्तियों की संख्या के आधार पर अनुमानित फ़ंक्शन के लघुगणक के मूल्यों को प्रस्तुत करते हैं। हरा रंग सिमुलेशन मापदंडों के अनुरूप रेटिंग को इंगित करता है।

अव्यक्त अवस्थाओं का अनुमान लगाने में त्रुटि अपेक्षाकृत कम है, लेकिन केवल तब जब प्रारंभिक सन्निकटन हम जो खोजना चाहते हैं, उससे बहुत भिन्न नहीं है। आपको यह समझने की आवश्यकता है कि बॉम-वेल्श एल्गोरिथम एक स्थानीय इष्टतम की खोज में एक कदम है, जिसका अर्थ है कि यह कभी भी वैश्विक चरम सीमा तक नहीं पहुंच सकता है।

सूत्र mathurl.com का उपयोग करके चित्रों में बदल जाते हैं। मुझे उम्मीद है कि किसी दिन, यहां सूत्रों को सरल और अधिक सुखद तरीके से सम्मिलित करना संभव होगा और वैसे, आर के लिए वाक्य रचना हाइलाइटिंग में बहुत कमी है।

छिपे हुए मार्कोव चेन, बॉम-वेल्श एल्गोरिथ्म

More articles: