अपाचे महतो। उपयोगकर्ता आत्मीयता मैट्रिक्स

नमस्कार।
मैं महट इन एक्शन किताब पढ़ रहा हूं। "मैं पुस्तक में देखता हूँ - मैं एक अंजीर देखता हूँ" का प्रभाव पड़ा। इसे खत्म करने के लिए, मैंने नोट लेने का फैसला किया।

Apache Mahout मशीन लर्निंग एल्गोरिदम के साथ काम करने के लिए एक पुस्तकालय है, जिसका उपयोग Hadoop या अपने दम पर ऐड-ऑन के रूप में किया जा सकता है। पुस्तकालय सहयोगी फ़िल्टरिंग , क्लस्टरिंग और वर्गीकरण विधियों को लागू करता है।

हम सहयोगी फ़िल्टरिंग के आधार पर एक सिफारिश प्रणाली पर विचार कर रहे हैं। यह उपयोगकर्ता-आधारित (उपयोगकर्ता-आधारित) या संपत्ति-उन्मुख (आइटम-आधारित) हो सकता है।

सहयोगात्मक फ़िल्टरिंग पूर्वानुमान विधियों में से एक है जो किसी उपयोगकर्ता समूह की ज्ञात प्राथमिकताओं (अनुमानों) का उपयोग किसी अन्य उपयोगकर्ता की अज्ञात प्राथमिकताओं का अनुमान लगाने के लिए करता है। उनकी मुख्य धारणा यह है: जिन्होंने अतीत में समान विषयों का मूल्यांकन किया है वे भविष्य में अन्य विषयों के समान मूल्यांकन देते हैं। (विकिपीडिया से)

उपयोगकर्ता-उन्मुख अनुशंसा प्रणालियों की मूल अवधारणाओं में से एक उपयोगकर्ता समानता का निर्धारण करने के लिए एक मीट्रिक है। मान लीजिए कि हमारे पास विभिन्न उपयोगकर्ताओं द्वारा फिल्मों के विचारों और रेटिंग पर डेटा है। हम दो उपयोगकर्ताओं की तुलना करेंगे: X और Y। उन्होंने फिल्मों में एक्स (एक्स ₁ , एक्स ₂ , ..., एक्स _एन ) और वाई (वाई ₁ , वाई ₂ , ..., वाई _एम ) का मूल्यांकन किया, जहां एन , एम क्रमशः पहले और दूसरे उपयोगकर्ताओं द्वारा दी गई रेटिंग की संख्या हैं। एन - दोनों उपयोगकर्ताओं द्वारा एक ही फिल्मों के लिए निर्धारित की गई रेटिंग की संख्या (पहली और दूसरी द्वारा देखी गई फिल्मों के सेट का प्रतिच्छेदन)। हम मानते हैं कि (x _i , y _i ) उपयोगकर्ताओं द्वारा एक फिल्म के लिए रखी गई रेटिंग की एक जोड़ी है।
Mahout कई एल्गोरिदम पर आधारित मैट्रिक्स को लागू करता है। मैं स्वयं एल्गोरिदम का वर्णन करता हूं, न कि महट में उनके कार्यान्वयन का।

पीयरसन सहसंबंध गुणांक (4.3.1)

कोष्ठकों में मैं ओवेन, अनिल, डिंगिंग, फ्रीडमैन की पुस्तक "एक्शन में महावत" को चिह्नित करूंगा।

महावत में कार्यान्वयन - पियर्सन सहसंबंधासन ।
पियर्सन का सहसंबंध गुणांक संख्या K (-1 ≤ K , 1) है , जो जोड़े में जाने वाली संख्याओं के दो सेटों की प्रवृत्ति दर्शाता है। यानी पहले और दूसरे सेट की संख्या के बीच लगभग एक रैखिक संबंध बनाते हैं। x _i = by _i (सभी i B के लिए यह लगभग समान होगा)। यदि निर्भरता रैखिक है, तो सहसंबंध गुणांक 1 है, यदि व्युत्क्रम -1 है, अगर कोई निर्भरता नहीं है, तो 0।

इसकी गणना सूत्र द्वारा की जाती है:

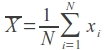
सही वेक्टर प्रविष्टि। - अंकगणित माध्य। इस तरह हम डेटा को केंद्र में रखते हैं। मैन्युअल रूप से गणना करते समय, इसे ध्यान में रखा जाना चाहिए, लेकिन महावत में सहसंबंध का कार्यान्वयन इस बात का ध्यान रखता है।

पियर्सन सहसंबंध मीट्रिक समस्याएं (4.3.2)

यह मानना ​​तर्कसंगत है कि दो उपयोगकर्ता जिन्होंने 200 समान फिल्में देखीं, वे दो उपयोगकर्ताओं की तुलना में अलग-अलग रेटिंग डालते हैं, जो तीन समान फिल्मों को देखते हैं और उन्हें एक ही रेटिंग देते हैं। लेकिन सूत्र से हमें विपरीत परिणाम मिलता है।
दूसरा दोष उन उपयोगकर्ताओं के लिए सहसंबंध की गणना करने की असंभवता है जिनकी केवल एक रेटिंग है (चूंकि भाजक शून्य होगा)।
गुणांक को उन मामलों के लिए भी परिभाषित नहीं किया गया है जब उपयोगकर्ताओं में से एक ने सभी फिल्मों को एक ही रेटिंग दी थी। उदाहरण के लिए, उपयोगकर्ता ने 3 फिल्में देखीं और उन्हें 5 की रेटिंग दी। फिर से, भाजक शून्य है।

सहसंबंध वजन (4.3.3)

पहली खामी को खत्म करने के लिए, सहसंबंध वजन की अवधारणा को पेश किया गया था। यदि गणना के लिए कई मापदंडों का उपयोग किया जाता है, तो सकारात्मक सहसंबंध 1 से गुणा किया जाता है, और नकारात्मक -1 से। इस प्रकार यदि बड़ी संख्या में समान फिल्में देखी गईं लेकिन विपरीत रेटिंग निर्धारित की गई, तो सहसंबंध सकारात्मक होगा।
यदि गुणांक की गणना करने के लिए कुछ मापदंडों का उपयोग किया गया था, तो आप 1 से भी कम संख्या से गुणा कर सकते हैं, जिससे उपयोगकर्ताओं की समानता कम हो सकती है।

यूक्लिडियन मीट्रिक (4.3.4)

महावत में कार्यान्वयन - यूक्लिडियनडिस्टेंससिमिलरिटी ।
कार्यान्वयन उपयोगकर्ताओं के बीच की दूरी का पता लगाना है। उपयोगकर्ता समन्वित अनुमानों के साथ एक बहुआयामी स्थान में बिंदुओं के रूप में कार्य करते हैं। फिल्म के लिए केवल दोनों उपयोगकर्ताओं द्वारा दी गई रेटिंग को ध्यान में रखा गया है।



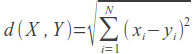
दूरी जितनी कम होगी, उपयोगकर्ताओं का स्वाद उतना ही अधिक होगा। इसलिए, Mahout ने K = 1 / (1 + d) में लागू किया गया मीट्रिक। पिछले मीट्रिक के विपरीत, यह 0 से 1 तक का मान लेता है। बड़ा गुणांक, उपयोगकर्ताओं के स्वाद के समान।

इस मीट्रिक का नुकसान यह है कि जो उपयोगकर्ता एक ही मूवी को रेट करते हैं (कोई अन्य सामान्य फिल्में नहीं हैं) उन लोगों की तुलना में अधिक समान होंगी, जिन्होंने लगभग एक ही तरह की सौ फिल्मों को रेट किया है।

कोसाइन फैक्टर (4.3.5)

Mahout कार्यान्वयन - PearsonCorrelationSimilarity का उपयोग करके ।
यह बिंदु O (0,0, ...) और उपयोगकर्ता बिंदु X (x ₁ , x ₂ , ...) , Y (y ₁ , y ₂ , ...) द्वारा बनाई गई दो पंक्तियों के बीच के कोण का कोसाइन है।
-1 ≤ कॉस ए । 1 । यदि कोण A = 0 (cos A = 1) है , तो उपयोगकर्ता समान हैं। यदि कोण A = 180 (cos A = -1) है , तो उपयोगकर्ताओं के स्वाद विपरीत हैं। यदि कोण 90 डिग्री के करीब है, तो इन दो उपयोगकर्ताओं की वरीयताओं के बीच कोई संबंध नहीं है। कॉशन गुणांक के बारे में अधिक जानें।

इस मीट्रिक के लिए महाउत में कोई विशेष कार्यान्वयन नहीं है; इसकी गणना के लिए पियर्सन सहसंबंध मीट्रिक का उपयोग किया जाता है। मैनुअल गणना नीचे दिए गए सूत्र के अनुसार की जा सकती है। दाईं ओर वेक्टर संकेतन पियर्सन के सहसंबंध से अलग है केवल हम निर्देशांक को केंद्र में नहीं रखते हैं।

स्पीयरमैन का सहसंबंध गुणांक (4.3.6)

महावत में क्रियान्वयन - स्पीयरमैन सहसंबंधस्मरण ।
स्पीयरमैन के सहसंबंध गुणांक को परिभाषित चर के बीच पियर्सन सहसंबंध गुणांक के रूप में परिभाषित किया गया है। सबसे कम पसंदीदा फिल्म को रेट किया गया है 1, अगले 2, आदि। सभी अनुमानों को स्थापित करने के बाद, पियर्सन सहसंबंध गुणांक की गणना की जाती है।

इस मीट्रिक का नुकसान धीमा काम है। आखिरकार, सहसंबंध गुणांक की गणना करने से पहले, आपको एक रैंकिंग आयोजित करने की आवश्यकता है। इसके अलावा, मीट्रिक में पियर्सन मीट्रिक में दोष हैं।

तनिमोटो अनुपात (4.3.7)

महतो में कार्यान्वयन - तनीमोतो कार्यकुशलता ।
टैनिमोटो गुणांक पहले और दूसरे दोनों उपयोगकर्ताओं (चौराहे) द्वारा भरे गए उपयोगकर्ताओं की संख्या का अनुपात है जो पहले और दूसरे (एसोसिएशन) के सभी गुणों की संख्या: के = आई / यू। यह मीट्रिक उन मामलों में उपयोग करने की सिफारिश की जाती है जहां वरीयता मान बूलियन हैं।

लॉग संभावना (4.3.8)

महौट में कार्यान्वयन - लॉजिकेलिहुडसिमिलरिटी ।
पिछले गणना के विपरीत, मीट्रिक गणना एल्गोरिथ्म पूरी तरह से सहज नहीं है।
पहले उपयोगकर्ता को n फिल्में देखने दें, मी दूसरा, p - दो उपयोगकर्ता कुल (एसोसिएशन) देखते हैं।



* - फिल्म को उपयोगकर्ता द्वारा मूल्यांकन नहीं किया गया है (या नहीं देखा गया)। 1 के बराबर अगर फिल्म रेट की जाती है, तो 0 के बराबर।








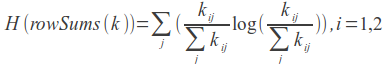
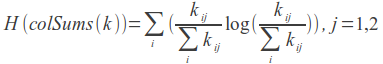LLR = 2 (H (k) - H (rowSums (k)) - H (colSums (k))) लॉग संभावना गुणांक है।

इस एल्गोरिथ्म के बारे में अधिक: सूत्र , कार्यान्वयन ।

मुझे खुशी होगी अगर कोई काम आएगा। हम पीएम में त्रुटियों के बारे में लिखते हैं, और टिप्पणियों में ट्रोल करते हैं।