👩‍❤️‍👨 ⛓️ 🌊 क्रमिक वंश द्वारा क्लस्टरिंग समस्या का समाधान 👩‍👧 🐎 ⚔️

नमस्कार। यह लेख ग्रेडिएंट डीसेंट विधि का उपयोग करके डेटा को क्लस्टर करने की विधि पर चर्चा करेगा। ईमानदारी से, यह विधि व्यावहारिक की तुलना में प्रकृति में अधिक अकादमिक है। मुझे मशीन सीखने के पाठ्यक्रम के प्रदर्शन उद्देश्यों के लिए इस पद्धति के कार्यान्वयन की आवश्यकता थी ताकि यह दिखाया जा सके कि कैसे विभिन्न कार्यों को विभिन्न तरीकों से हल किया जा सकता है। यद्यपि, निश्चित रूप से, यदि आप एक अलग-अलग मीट्रिक का उपयोग करके डेटा को क्लस्टर करने की योजना बनाते हैं, जिसके लिए एक निश्चित डेटा सेट पर ग्रेडिएंट की गणना करने की तुलना में सेंट्रोइड का पता लगाना कठिन है, तो यह विधि उपयोगी हो सकती है। इसलिए यदि आप रुचि रखते हैं कि आप क्रमिक वंश विधि का उपयोग करके एक सामान्यीकृत मीट्रिक के साथ k- साधन क्लस्टरिंग समस्या को कैसे हल कर सकते हैं, तो मैं बिल्ली के नीचे पूछता हूं। कोड में आर।

डेटा

सबसे पहले, आइए बहुत सारे डेटा पर चर्चा करें, जिस पर हम एल्गोरिदम का परीक्षण करेंगे। परीक्षण के लिए, स्मार्टफोन के सेंसर से बहुत सारे डेटा का उपयोग किया जाता है : 7352 टिप्पणियों में कुल 563 फ़ील्ड; उपयोगकर्ता आईडी और कार्रवाई के प्रकार के लिए नीचे से 2 फ़ील्ड हाइलाइट किए गए हैं। कुल 6 क्रियाओं (वॉकिंग, वॉकिंग_अपस्टार, वॉकिंग_डाउस्टएयरस, सिटिंग, स्टैनिंग, लाईंग) के लिए, सेंसर की रीडिंग के आधार पर उपयोगकर्ता क्रियाओं को वर्गीकृत करने के लिए बहुत कुछ बनाया गया है। आप उपरोक्त लिंक पर सेट का अधिक विस्तृत विवरण पा सकते हैं।

जैसा कि आप समझते हैं, आयामों को कम किए बिना ऐसे सेट की कल्पना करना थोड़ा समस्याग्रस्त है। आयाम को कम करने के लिए, प्रमुख घटक विधि का उपयोग किया गया था , इसके लिए आप मानक आर भाषा टूल का उपयोग कर सकते हैं, या मेरी रिपॉजिटरी से उसी भाषा में इस पद्धति को लागू कर सकते हैं। आइए एक नज़र डालते हैं कि पहले और तीसरे मुख्य घटक पर मूल सेट क्या दिखता है।

कोड

m.proj <- ProjectData(m.raw, e$eigenVectors[, c(1, 3)]) plot(m.proj[, 1], m.proj[, 2], pch=19, col=rainbow(6)[unclass(as.factor(samsungData$activity))], xlab="first", ylab="third", main="Two components; actions")

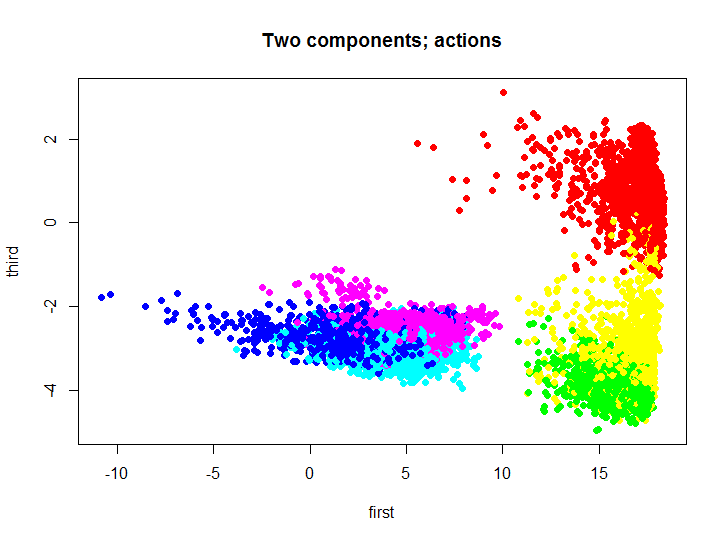
अलग-अलग रंग अलग-अलग क्रियाओं को दर्शाते हैं, फिर हम क्लस्टरिंग के परिणामों के परीक्षण और कल्पना के लिए इस दो-आयामी सेट का उपयोग करेंगे।

K- साधन एल्गोरिथ्म लागत समारोह

हम निम्नलिखित संकेतन प्रस्तुत करते हैं:

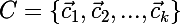- कई सेंट्रोइड्स 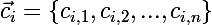संबंधित समूह
- मूल डेटा सेट को क्लस्टर किया जाएगा
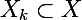Kth क्लस्टर, मूल सेट का सबसेट है

अब शास्त्रीय k- साधन एल्गोरिथ्म की लागत समारोह पर विचार करें:

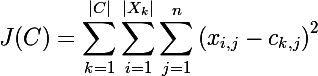
यानी एल्गोरिथ्म सेंट्रो से क्लस्टर तत्वों के कुल द्विघात विचलन को कम करता है। दूसरे शब्दों में, इसी केन्द्रक से क्लस्टर तत्वों के यूक्लिडियन दूरी के वर्गों का योग न्यूनतम किया जाता है:

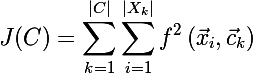
, जहां एफ - इस मामले में यूक्लिडियन दूरी है।

जैसा कि आप जानते हैं, इस समस्या को हल करने के लिए उम्मीद-अधिकतमकरण एल्गोरिथ्म पर आधारित एक प्रभावी शिक्षण एल्गोरिथ्म है । आइए R में निर्मित फ़ंक्शन का उपयोग करके इस एल्गोरिदम के परिणाम पर एक नज़र डालें:

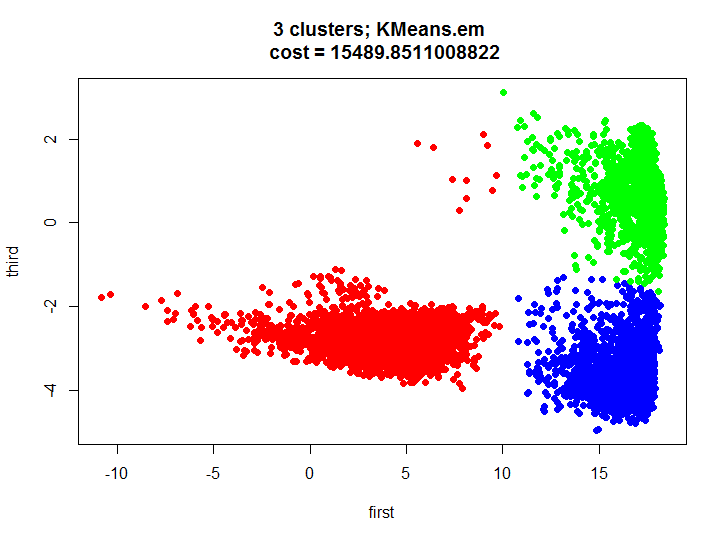
कोड

 kmeans.inner <- kmeans(m.proj, 3) plot(m.proj[, 1], m.proj[, 2], pch=19, col=rainbow(3)[unclass(as.factor(kmeans.inner$cluster))], xlab="first", ylab="third", main=paste(k, " clusters; kmeans \n cost = ", kmeans.inner$tot.withinss/2, sep=""))

धीरे-धीरे उतरना

ग्रेडिएंट डीसेंट अल्गोरिथम अपने आप में काफी सरल है, लब्बोलुआब यह है कि ग्रेडिएंट डायरेक्शन के विपरीत दिशा में छोटे चरणों में ले जाना है, उदाहरण के लिए , एरर बैक प्रोपेगेशन एल्गोरिदम काम करता है, या एक सीमित बोल्टमैन मशीन के प्रशिक्षण के लिए कंट्रास्ट डाइवरेज एल्गोरिथ्म । सबसे पहले, मॉडल मापदंडों के संबंध में उद्देश्य फ़ंक्शन की ग्रेडिएंट या उद्देश्य फ़ंक्शन के आंशिक डेरिवेटिव की गणना करना आवश्यक है।

चूँकि हमने क्लासिक k- साधनों के बारे में अनुभाग छोड़ दिया है, तो f हो सकता है, सिद्धांत रूप में, दूरी का कोई भी माप, जरूरी नहीं कि यूक्लिडियन मीट्रिक हो

लेकिन एक समस्या है, हम इस स्तर पर नहीं जानते हैं कि सेट X का क्लस्टर में विभाजन क्या है। आइए उद्देश्य फ़ंक्शन को इस तरह से सुधारने की कोशिश करें कि इसे एक सूत्र के रूप में लिखा जा सके, जो कि अंतर करना आसान होगा: सेट के प्रत्येक तत्व से न्यूनतम दूरी का योग तीन सेंटीमीटर तक। यह सूत्र इस प्रकार है:

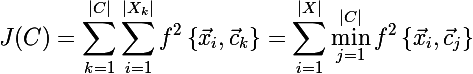
आइए अब नए उद्देश्य फ़ंक्शन के व्युत्पन्न का पता लगाएं:

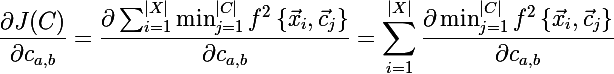
खैर, यह पता लगाना बाकी है कि न्यूनतम व्युत्पन्न क्या है, लेकिन सब कुछ सरल हो जाता है: अगर a- सेंट्रोइड वास्तव में वह है जिसमें सेट के वर्तमान तत्व से दूरी कम है, तो अभिव्यक्ति का व्युत्पन्न वेक्टर तत्व के संबंध में दूरी के वर्ग के व्युत्पन्न के बराबर है, अन्यथा मामला शून्य है:

विधि कार्यान्वयन

जैसा कि आप समझते हैं, पिछले पैराग्राफ से सभी चरणों को दूरी को चुकता किए बिना किया जा सकता है। इस पद्धति को लागू करते समय ऐसा किया गया था। विधि दूरी समारोह और दो वेक्टर के बीच दूरी समारोह के आंशिक व्युत्पन्न की गणना समारोह के रूप में प्राप्त करता है दूसरे वेक्टर के घटक के संबंध में, मैं उदाहरण के लिए "आधा यूक्लिडियन दूरी वर्ग" (यह व्युत्पन्न के बाद से उपयोग करने के लिए सुविधाजनक है), साथ ही ढाल वंश समारोह भी। :

दूरी के कार्य

दूरी समारोह

 HalfSqEuclidian.distance <- function(u, v) { # Half of Squeared of Euclidian distance between two vectors # # Args: # u: first vector # v: second vector # # Returns: # value of distance return(sum((uv)*(uv))/2) }

आंशिक व्युत्पन्न कार्य

 HalfSqEuclidian.derivative <- function(u, v, i) { # Partial derivative of Half of Squeared of Euclidian distance # between two vectors # # Args: # u: first vector # v: second vector # i: index of part of second vector # # Returns: # value of derivative of the distance return(v[i] - u[i]) }

क्रमिक वंश विधि

 KMeans.gd <- function(k, data, distance, derivative, accuracy = 0.1, maxIterations = 1000, learningRate = 1, initialCentroids = NULL, showLog = F) { # Gradient descent version of kmeans clustering algorithm # # Args: # k: number of clusters # data: data frame or matrix (rows are observations) # distance: cost function / metrics # centroid: centroid function of data # accuracy: accuracy of calculation # learningRate: learning rate # initialCentroids: initizalization of centroids # showLog: show log n <- dim(data)[2] c <- initialCentroids InitNewCentroid <- function(m) { c <- data[sample(1:dim(data)[1], m), ] } if(is.null(initialCentroids)) { c <- InitNewCentroid(k) } costVec <- vector() cost <- NA d <- NA lastCost <- Inf for(iter in 1:maxIterations) { g <- matrix(rep(NA, n*k), nrow=k, ncol=n) #calculate distances between centroids and data d <- matrix(rep(NA, k*dim(data)[1]), nrow=k, ncol=dim(data)[1]) for(i in 1:k) { d[i, ] <- apply(data, 1, FUN = function(v) {distance(v, c[i, ])}) } #calculate cost cost <- 0 for(i in 1:dim(data)[1]) { cost <- cost + min(d[, i]) } if(showLog) { print(paste("Iter: ", iter,"; Cost = ", cost, sep="")) } costVec <- append(costVec, cost) #stop conditions if(abs(lastCost - cost) < accuracy) { break } lastCost <- cost #calculate gradients for(a in 1:k) { for(b in 1:n) { g[a, b] <- 0 for(i in 1:dim(data)[1]) { if(min(d[, i]) == d[a, i]) { g[a, b] <- g[a, b] + derivative(data[i, ], c[a, ], b) } } } } #update centroids for(a in 1:k) { for(b in 1:n) { c[a, b] <- c[a, b] - learningRate*g[a, b]/dim(data)[1] } } } labels <- rep(NA, dim(data)[1]) for(i in 1:dim(data)[1]) { labels[i] <- which(d[, i] == min(d[, i])) } return(list( labels = labels, cost = costVec )) }

परीक्षण

 KMeans.gd.result <- KMeans.gd(k, m.proj, HalfSqEuclidian.distance, HalfSqEuclidian.derivative, showLog = T) plot(m.proj[, 1], m.proj[, 2], pch=19, col=rainbow(k)[unclass(as.factor(KMeans.gd.result$labels))], xlab="first", ylab="third", main=paste(k, " clusters; KMeans.gd \n cost = ", KMeans.gd.result$cost[length(KMeans.gd.result$cost)], sep=""))

आइए क्लस्टरिंग के परिणाम पर एक नज़र डालें और सुनिश्चित करें कि यह लगभग समान है।

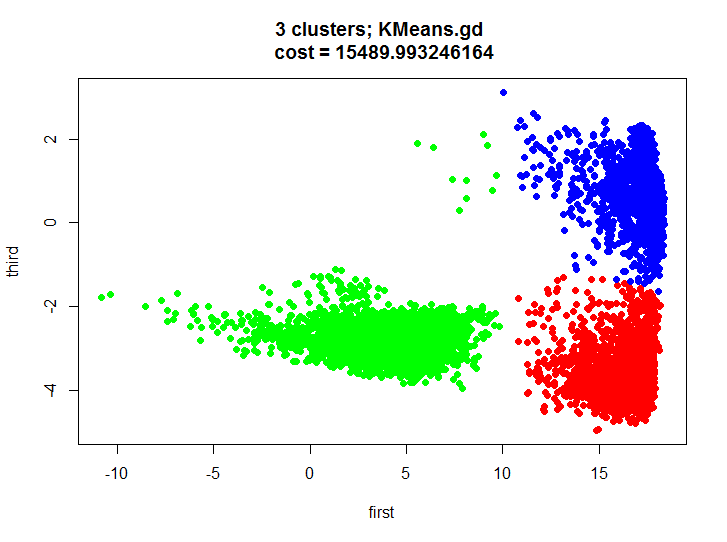
और यह दोनों एल्गोरिदम के लिए पुनरावृति से लागत समारोह के मूल्य की गतिशीलता जैसा दिखता है:

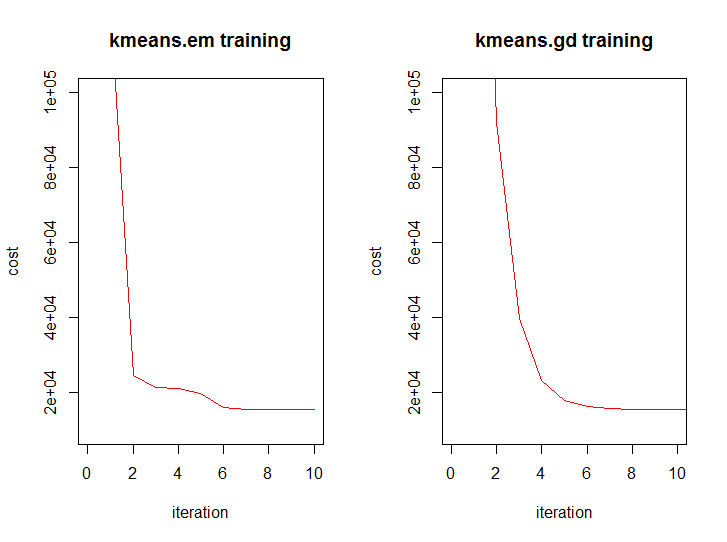
निष्कर्ष

पहले, आइए हमारे परीक्षण में क्या हुआ, इसके बारे में कुछ शब्द बताते हैं। हमें तीन समूहों में दो आयामी सेट का एक शानदार विभाजन मिला, हम देखते हैं कि क्लस्टर अधिक ओवरलैप नहीं करते हैं और हम पूरी तरह से प्रत्येक क्लस्टर के लिए क्रियाओं को पहचानने के लिए मॉडल बना सकते हैं, जिससे कुछ हाइब्रिड मॉडल प्राप्त होते हैं (एक क्लस्टर में मुख्य रूप से एक कार्रवाई होती है, अन्य दो, और तीसरा तीन)।

आइए हम यूक्लिडियन दूरी का उपयोग करके क्लस्टरिंग में एल्गोरिदम की जटिलता पर एक नज़र डालें, केवल एक पुनरावृत्ति पर विचार करें (पुनरावृत्तियों की संख्या का विश्लेषण एक तुच्छ कार्य नहीं है)। आज्ञा देना k की संख्या हो समूहों, n डेटा आयाम है, मीटर डेटा की राशि है (k <= m)। चरम मामले में, के = मी।

EM संस्करण:
जीडी संस्करण:

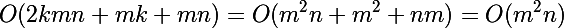
सामान्य तौर पर, गणितीय रूप से, दोनों एल्गोरिदम समान स्तर पर हैं, लेकिन हम जानते हैं कि एक थोड़ा अधिक है।

आप यहाँ सभी कोड पा सकते हैं ।

क्रमिक वंश द्वारा क्लस्टरिंग समस्या का समाधान

डेटा

K- साधन एल्गोरिथ्म लागत समारोह

धीरे-धीरे उतरना

विधि कार्यान्वयन

निष्कर्ष

More articles: