पी को एक विषम प्रधानता दें। यह काफी व्यापक रूप से ज्ञात है कि p को पूर्णांकों के दो वर्गों के योग के रूप में दर्शाया जा सकता है p = a ² + b ² यदि और केवल यदि p को 4 से विभाजित किया जाए तो शेष 1: 5 = 1 ² +2 ² , 13 = 3 ² +2 होता है। ² , 17 = 1 ² +4 ² , ...; 3, 7, 11, ... अप्राप्य हैं। यह बहुत कम ज्ञात है कि ए और बी को एक सुंदर सूत्र के साथ लिखा जा सकता है जो सीधे एक अण्डाकार वक्र से संबंधित है। हम 1907 के इस परिणाम के बारे में बात करेंगे , एक जर्मन लेखक के नाम के कारण जैकबस्टल और संबंधित चीजों के बारे में।

यह समझना काफी आसान है कि 3, 7, 11 और अन्य संख्याएँ जो 4 से विभाजित होने पर शेष 3 देती हैं, ² + b ² के रूप में प्रतिनिधित्व करने योग्य नहीं हैं: सम संख्या का वर्ग हमेशा 4 से विभाजित होता है, विषम संख्या का वर्ग हमेशा शेष 1 देता है जब 4 से विभाजित किया जाता है। , 4 से विभाजित होने पर दो वर्गों का योग 0, 1 या 2 रख सकता है, लेकिन 3 नहीं। फॉर्म 4k + 1 की अभाज्य संख्याओं का प्रतिनिधित्व स्पष्ट नहीं है (विशेषकर यदि आप ध्यान दें कि सादगी आवश्यक है: संख्या 21, हालांकि यह वांछित शेष है, दो का योग है कोई वर्ग नहीं)।

कटौती

असीम रूप से कई प्राकृतिक संख्याएं हैं। कुछ आधारों पर उन्हें कक्षाओं में संयोजित करना उपयोगी हो सकता है। विशेष रूप से, विभाजन के शेष भाग को कुछ संख्या n से जोड़कर अवशेष modulo n की ओर ले जाता है: अवशेष x all सभी संख्याओं का वह वर्ग है, जिसे n द्वारा विभाजित करने पर x के समान शेषफल देते हैं। जो समतुल्य है, अवशेषों x̅ में x + n where k फॉर्म के सभी नंबर होते हैं, जहां k एक पूर्णांक होता है। इस पद के ढांचे के भीतर, सभी अवशेष मोडुलो पी (परिचय से समान विषम प्रधानमंत्री) होंगे। स्वाभाविक रूप से, वहाँ कई अलग-अलग अवशेष हैं क्योंकि पी द्वारा विभाजित होने से अवशेष हो सकते हैं, अर्थात बिल्कुल पी । प्राकृतिक संख्याओं की अनंतता की तुलना में, अवशेषों के लिए संक्रमण विकल्पों की संख्या को बहुत कम कर देता है।
कक्षा संचालन हमेशा समझ में नहीं आता है। उदाहरण के लिए, यौगिक संख्याओं के वर्ग में एक वर्ग के अपराधों को जोड़ने का प्रयास बहुत सार्थक नहीं है: हम केवल संख्याओं को जोड़ सकते हैं, और एक अभाज्य संख्या और एक समग्र संख्या के गुण वर्ग के लिए सामान्य नहीं दिखाते हैं। हालांकि टॉटोलॉजी क्लब के सदस्य कह सकते हैं कि अपराधों की श्रेणी और यौगिक संख्याओं के वर्ग को जोड़ने से संख्याओं का एक वर्ग प्राप्त होता है जिसे एक अभाज्य संख्या और एक यौगिक संख्या के योग में अभिव्यक्त किया जा सकता है।

कटौती के लिए, हालांकि, इसके अलावा, घटाव और गुणा प्राकृतिक संख्या से "विरासत में मिला" अन्य कटौती देते हैं। उदाहरण के लिए, 2 any + 3̅ = 5̅: 2 के शेष के साथ किसी भी संख्या को लीजिए, 3 के शेष के साथ कोई भी संख्या, और उनकी राशि निश्चित रूप से 5. का शेष देगी। आम तौर पर, दो नॉनज़रो अवशेषों के उत्पाद modulo के मनमाने ढंग से अचानक शून्य होने की संभावना है, 2̅ ∙ 3̅ = 0̅ में शून्य। मॉड्यूल 6, जो अप्रिय है। लेकिन एक साधारण मॉड्यूल के मामले में, जाहिर है, ऐसा नहीं होता है, जैसा कि वे कहते हैं, कोई शून्य विभाजक नहीं हैं। इसके अलावा, हम समीकरण a resid = 0̅ को छोड़कर, किसी भी दो अवशेषों के लिए समीकरण a̅ ̅ x̅ = b division (विभाजन ऑपरेशन) हल कर सकते हैं, और परिणाम विशिष्ट रूप से निर्धारित किया जाएगा। विशिष्टता इस तथ्य से अनुसरण करती है कि नॉनज़रो अवशेषों का उत्पाद नॉनज़ेरो है। चूंकि a Since ̅ 0̅ , a और p का सबसे बड़ा सामान्य कारक 1 है (सादगी p की यहाँ भी आवश्यकता है), विस्तारित यूक्लिडियन एल्गोरिथ्म में x और y इस तरह मिलेंगे कि एक ∙ x + p = y = 1 , जिसका अर्थ है a̅ ∙ x̅ = 1̅ , जिसका अर्थ है कि a̅ ∙ (b̅ that x =) = b̅ ।

शून्य विभाजक की अनुपस्थिति का एक महत्वपूर्ण परिणाम: डिग्री एन के एक एकल चर में एक नॉनज़ेरो बहुपद एन जड़ों से अधिक नहीं हो सकता है। (यह सामान्य पूर्णांक के लिए अच्छी तरह से जाना जाता है, लेकिन अवशेषों के संचालन का उपयोग करते समय, इसके लिए अतिरिक्त औचित्य की आवश्यकता होती है: समीकरण 3̅ ̅ x∙ = 0̅ मोडुलो 6 में तीन समाधान 0̅, 2), 4) होते हैं।) वास्तव में, सामान्य "विभाजन" दिखाता है कि कोई भी। बहुपद f (x) को f (x) = (x-c) g (x) + (कुछ स्थिर) के रूप में दर्शाया जा सकता है, जहाँ बहुपद g (x) में एक डिग्री कम होती है; यदि c , f (x) की जड़ है, तो स्थिर शून्य (विकल्प x = c ) है; यदि c ' f (x) की एक और जड़ है, तो यह g (x) की जड़ होगी ( शून्य विभाजक की अनुपस्थिति यहां महत्वपूर्ण है), इसलिए प्रक्रिया को जारी रखा जा सकता है। यदि n जड़ें पहले से जमा हैं, तो शेष g (x) एक स्थिर, अतिरिक्त, गैर-शून्य (अन्यथा f (x) = 0 ) होगी और जिसकी कोई अधिक जड़ नहीं है।

एक साधारण मॉड्यूल द्वारा कटौती को जोड़ा, घटाया और गुणा किया जा सकता है। गैर-शून्य कटौती को विभाजित किया जा सकता है। इन सभी परिचालनों में सामान्य गुण operations ̅ b̅ = b∙ ̅ a । स्मार्ट पुस्तकों का कहना है कि एक साधारण मॉड्यूल द्वारा कटौती एक क्षेत्र बनाती है (और एक यौगिक मॉड्यूल द्वारा कटौती, जहां विभाजित करना असंभव है, और बाकी सब एक ही है, एक कम्यूटेटिव रिंग है )। और किसी को इस क्षेत्र को परिमित कहने के लिए एक स्मार्ट पुस्तक नहीं होना चाहिए। अवशेष क्षेत्र केवल परिमित क्षेत्र नहीं है, लेकिन हमें अन्य अंतिम क्षेत्रों की आवश्यकता नहीं होगी।

अंडाकार घटता के बारे में थोड़ा सा

अण्डाकार वक्र मोदुलो पी (उसी विषम प्राइम) को समीकरण y ² = x ³ + ₂ x ² + a ₄ x + a ₆ के समीकरणों के समुच्चय के रूप में माना जा सकता है, जहाँ x , y और सभी एक अवशिष्ट हैं (प्रत्येक समाधान को एक कहा जाता है बिंदु ), प्लस एक विशेष बिंदु O जिसमें एक जोड़ी x, y नहीं है । समीकरण के दाईं ओर को एक वर्ग से विभाजित नहीं किया जाना चाहिए, अन्यथा यह एक अण्डाकार वक्र नहीं होगा: प्रकार y ² = (x-1̅) ² (x + 2̅) के समीकरण में, आप चर y को z / y (x-1̅) से बदल सकते हैं और निर्भरता प्राप्त कर सकते हैं दूसरी डिग्री, तीसरी नहीं।
यदि p can 3 , तो वेरिएबल x के बजाय हम x + 2/3 getting ले सकते हैं, x ^{2 के} साथ पद से छुटकारा पा सकते हैं।

यह स्पष्ट है कि चूंकि x, y एक परिमित समुच्चय से संबंधित है, अण्डाकार वक्र पर बिंदुओं की संख्या भी परिमित है। उनमें से कितने? यह एक सामान्य रूप से कठिन प्रश्न है। हम खुद को प्रपत्र y ² = x ³ -k । X के घटता तक सीमित रखते हैं। इस तरह के घटता के लिए, पूरा प्रमाण एक हैबर पोस्ट में रखा जा सकता है (यद्यपि एक लंबे समय तक)।

द्विघात कटौती और गैर-कटौती

आइए पहले हम एक सरल प्रश्न पूछें। समीकरण y ² = c में कितने समाधान हैं , जहां y, c अवशेष हैं? पी = 7 के लिए उदाहरण:

y	0	1	2	3	4	5	6
य ^२	0	1	4	2	2	4	1

यदि c = 0 = , तो एक समाधान है, y = 0̅ । शेष y मानों को 1 the से घटाकर (p-1) / 2 , और कटौती से (p + 1) / 2 , -1̅ तक दो हिस्सों में बांटा गया है। Y ² = (- y) ^{2 के} बाद से, y ² के मानों की पंक्ति का दूसरा भाग पहली छमाही में दर्पण सममित है। दूसरी ओर, प्रत्येक आधे में कोई पुनरावृत्ति नहीं होती है, क्योंकि अन्यथा समीकरण में कम से कम 4 समाधान होंगे, जो कि डिग्री के एक बहुपद के लिए असंभव है। इसलिए, वहाँ (p-1) / 2 अवशेष हैं c जिसके लिए ठीक 2 समाधान हैं, और एक ही संख्या अवशेष c , जिसके लिए कोई समाधान नहीं हैं।

सी के नॉनज़ेरो अवशेष जिसके लिए एक समाधान है उसे द्विघात अवशेष कहा जाता है। जिन अवशेषों का कोई समाधान नहीं है, उन्हें द्विघात अवशेष कहा जाता है। यह ध्यान देने योग्य है कि एक द्विघात गैर-कटौती एक कटौती है, यह सिर्फ इतना है कि वह द्विघात होने के लिए भाग्यशाली नहीं था। पौराणिक प्रतीक 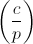$\ बायाँ (\ frac cp \ right)$ c से वर्गों का संबंध दर्शाता है: 1 यदि यह लागू होता है (यानी, c एक द्विघात अवशेष है), -1 यदि यह नहीं होता (अर्थात, c एक द्विघात अवशेष है), 0 यदि c = 0̅ है । समीकरण y ² = c के समाधानों की संख्या है $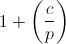1+ \ बायाँ (\ frac cp \ right)$ ।

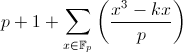
वापस अण्डाकार वक्रों के लिए। हम निश्चित x के लिए विकल्प y की संख्या जानते हैं, वक्र y ² = x ³ -k down x पर कुल अंकों की संख्या को सभी x पर संक्षेप द्वारा लिखा जा सकता है और विशेष बिंदु के बारे में नहीं भूलना चाहिए: $p + 1 + \ sum_ {x \ in \ mathbb {F} _p} \ left (\ frac {x ^ 3-kx} p \ right)$ । प्रतीक F _{p के द्वारा} , जो पहले प्रकट नहीं हुआ था, यह अवशेषों modulo p के क्षेत्र (क्षेत्र) को निरूपित करने के लिए प्रथागत है।

अब हम दो वर्गों के योग में p के विस्तार के घटकों के लिए दिए गए सूत्रों को प्रस्तुत करने के लिए तैयार हैं। प्रमेय। आज्ञा देना जी किसी भी द्विघात अवशेष है। यदि p को 4 से विभाजित किया जाता है, तो शेष 1 देता है
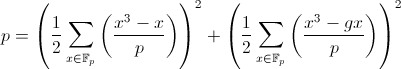
$p = \ बाएँ (\ frac12 \ sum_ {x \ in \ mathbb {F} _p} \ left (\ frac {x ^ 3-x} {p} \ right) \ right) ^ 2 + \ बाएँ (\ frac12) sum_ {x \ in \ mathbb {F} _p} \ left (\ frac {x ^ 3-gx} {p} \ right) \ right) ^ 2$
और पहले ब्रैकेट में संख्या एक अजीब पूर्णांक है, दूसरे ब्रैकेट में संख्या एक पूर्णांक है। यदि पी, जब 4 से विभाजित किया जाता है, तो शेष 3 देता है, तो कोष्ठक में दोनों योग शून्य होते हैं (जिसका अर्थ है कि अंडाकार घटता पर अंक की संख्या p + 1 है )।

सबूत

चूंकि पोस्ट पहले से ही लंबी है, इसलिए स्पॉइलर के नीचे प्रूफ को हटा दिया जाता है। धारणा से समझौता किए बिना इसे सुरक्षित रूप से छोड़ दिया जा सकता है।

भाग 1. केस पी = 4k + 3 और समता / विषमता मुद्दे।

यदि हम एक नॉनज़ेरो रेसिड्यू c लेते हैं और इसे 1̅ से p̅-1ues तक सभी अवशेषों से गुणा करते हैं, तो सभी उत्पाद नॉनज़रो और पेयर वाइज अलग-अलग होते हैं (यदि c = x = c , y , तो c x (xy = 0̅) , जो nonzero c के लिए हो सकता है केवल अगर x = y ), जिसका अर्थ है कि यह 1̅ से p̅-1̅ तक सभी अवशेषों के किसी प्रकार का क्रमचय होगा । इसलिए, 1∙ ̅ 2̅ ∙ ... ̅ (p̅-1 =) = (c ̅ 1̅) ∙ (c ∙ 2̅) ∙ ... ∙ (c ∙ (p̅-1̅)) = c ^p-1 ∙ 1̅ ∙ 2̅ ∙ ... ∙ (p̅-1̅) और c ^p-1 = ¹ any किसी भी नॉनवेज अवशेषों के लिए। (यह फ़र्मेट की छोटी प्रमेय का प्रमाण था।)

इसलिए, बहुपद x ^p-1 -1 = (x ^{(p-1) / 2} -1) (x ^{(p-1) / 2} +1) में p-1 जड़ें होती हैं। इसलिए, प्रत्येक ब्रैकेट में (पी -1) / 2 जड़ें (कोष्ठक की डिग्री के लिए अधिकतम संभव संख्या) है। प्रत्येक द्विघात अवशेष पहले ब्रैकेट की जड़ है (यदि x = c ² , तो x ^{(p-1) / 2} = c ^p-1 = 1ue ), उनमें से (p-1) / 2 हैं , जिसका अर्थ है कि दूसरा वर्ग सभी द्विघात अवशेषों के लिए बना हुआ है। तो, ग के लेजेंड्रे प्रतीक c ^{(p-1) / 2} के समान अवशेष के हैं। (यह यूलर की कसौटी का प्रमाण था)।

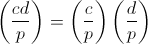
नतीजतन, हम प्राप्त करते हैं $\ बायाँ (\ frac {cd} p \ right) = \ बाएँ (\ frac cp \ right) \ बाएँ (\ frac dp \ right)$ ।

-1 Is एक द्विघात अवशेष है? संकेत (-1) ^(पी -1 ^{) / 2} पर निर्भर करता है। यदि 4 से विभाजित होने पर p शेष 1 देता है, तो (p-1) / 2 सम है, (-1) ^{(p-1) / 2} = 1 , -1̅ द्विघात अवशिष्ट है। यदि पी, जब 4 से विभाजित किया जाता है, तो शेष 3 देता है, तो सब कुछ इसके विपरीत है और -1 when एक द्विघात गैर-अवशेष है।

प्रमेय का सरल भाग: p शेष 3 देता है जब 4 से विभाजित किया जाता है। फिर, प्रत्येक ब्रैकेट में, x और -x के साथ पद लिजेंड्रे प्रतीक द्वारा एक-दूसरे से भिन्न होते हैं -1 एफटीपी से, यानी, वे साइन में विपरीत हैं और 0. अप तक जोड़ते हैं। सभी शब्दों से, x = 0 sum को छोड़कर, उन्हें शून्य योग वाले जोड़े में विभाजित किया गया है, और x = 0̅ के साथ शब्द शून्य है, पूरी राशि 0 है।

यदि p 4 से विभाजित होने पर शेष 1 देता है, तो x और -x के साथ शब्द बराबर हैं और उनका योग सम है। तो, पूरी राशि भी है और कोष्ठक में संख्या वास्तव में पूर्णांक हैं। रुकने के बाद समता / विषमता अधिक जटिल नहीं है: प्रमेय के पहले वर्ग में तीन शून्य शब्द हैं, शेष शर्तें (p-3) / 2 जोड़े में विभाजित हैं, प्रत्येक जोड़ी में; 2 के योग के साथ; किसी भी संकेत के साथ जब 4 से विभाजित किया जाता है, तो शेष 2 होता है, 4 से विभाजित करने पर पूरी राशि शेष बच जाती है जो कि पी -3 के समान होती है, यानी 2. आधे में विभाजित होने के बाद, हमें एक विषम संख्या मिलती है। प्रमेय के दूसरे ब्रैकेट में and 2 के साथ केवल एक शून्य शब्द और (पी -1) / 2 जोड़े हैं, 4 से विभाजित होने से अंतिम शेष 0 निकला, आधे में विभाजित होने के बाद भी एक समान संख्या बनी हुई है।

भाग 2. मामला p = 4k + 1।

पी, जब 4 से विभाजित किया जाता है, तो शेष दें 1. प्रमेय के पहले ब्रैकेट को ए से , दूसरे को बी से चिह्नित करें । हम पहले से ही जानते हैं कि ए और बी पूर्णांक हैं।

यह साबित करने के लिए, हम दो तरह से गणना करते हैं निम्नलिखित अजीब मात्रा एन : अवशेषों की पत्नियों की संख्या ( x ₁ , y ₁ , x ₂ , y ₂ , t ) जैसे कि दो समीकरण एक साथ संतुष्ट हैं: y ₁ ² = x ₁ ³ -t∙ x ₁ और y ₂ ² = x ₂ ³ -t x x ₂ ।

पहली विधि में, हम पहले t को ठीक करते हैं और x, y से चार की संख्या की गणना करते हैं, जिसके बाद हम सभी t के लिए परिणाम जोड़ते हैं। यह स्पष्ट है कि निश्चित टी के लिए, युग्म ( x ₁ , y ₁ ) वक्र y ² = x ³ -t , x का कोई भी विशेष-विशेष बिंदु हो सकता है , दूसरी जोड़ी ( x ₁ , y ₁ ) समान वक्र का कोई भी विशेष-बिंदु हो सकता है, और ऐसे जोड़े की कुल संख्या गैर-विशेष बिंदुओं की संख्या के वर्ग के बराबर है। (वास्तव में, इसीलिए हम एक अजीब मात्रा पर विचार कर रहे हैं, यह हमें ² और b ^{2 के} करीब आने की अनुमति देता है ^। ) यदि t = 0 है , तो समीकरण y ² = x ³ , जैसा कि पहले ही उल्लेख किया गया है, एक अण्डाकार वक्र को परिभाषित नहीं करता है और समीकरण के रूप में कई हैं। z ² = x (जहां y = z = x ), यानी, बिल्कुल पी । टी = 1 के लिए , पी + 2 ए समाधान प्राप्त किए जाते हैं, टी = जी - पी + 2 बी समाधानों के लिए। अन्य टी मूल्यों के बारे में क्या?

यदि y ² = x ³ -t ³ x और c कुछ गैर-अक्षीय अवशेष हैं, तो c ⁶ y ² = c ⁶ x ³ -c ⁶ t , x , जो (c ³ y) ² = (c ² x) के बराबर है ³ -सी ⁴ टी ∙ (सी ² एक्स) । दूसरे शब्दों में, यदि (x, y) t के साथ एक समीकरण का हल है, तो (c ² x, c ³ y) c ⁴ t के साथ समीकरण का हल है, इसलिए समाधानों की संख्या t और c ⁴ t के साथ मेल खाती है । फॉर्म ⁴ सी के कितने अलग-अलग नॉनजेरो अवशेष हैं? एक तरफ, कम से कम (p-1) / 4 : (p-1) c के मान "एक साथ चिपक सकते हैं" 4 से अधिक नहीं के समूहों में। दूसरी ओर, यदि (p-1) / 4 पूर्णांक है, तो सभी इस तरह के अवशेष बहुपद x ^{(p-1) / 4} -1 की जड़ें हैं, ताकि उनमें अधिक (p-1) / 4 न हो। इसलिए, उनमें से वास्तव में (पी -1) / 4 हैं ।
तो, (p-1) / 4 वक्रों में p + 2a गैर-विशेष अंक हैं, दूसरे (p-1) / 4 वक्रों में p + 2b गैर-विशेष अंक हैं। यह पहले से ही जरूरत का आधा हिस्सा है।

यदि y ² = x ³ -t , x , तो g ³ y ² = (g ∙ x) ³ - (g ² t) (g t x) । एक निश्चित x के लिए, समीकरण g ³ y ² = ... के समाधानों की संख्या 2 है - समीकरण y ^{2 s} के समाधानों की संख्या ...। इसलिए, t = g ² (और इसलिए (p-1) / 4 समान वक्रों) के साथ वक्र पर गैर-विशेष बिंदुओं की संख्या 2p- (p + 2a) = p-2a है । इसी प्रकार, t = g ^{3 के} साथ वक्र पर गैर- विशेष बिंदुओं की संख्या 2p- (p + 2b) = p-2b है ।

तो, पहली गणना विधि देता है
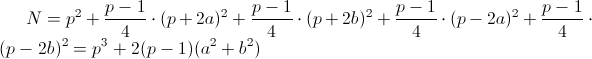$N = p ^ 2 + \ frac {p-1} 4 \ cdot (p + 2a) ^ 2 + \ frac {p-1} 4 \ cdot (p + 2b) ^ 2 + \ frac {p-1}: 4 \ cdot (p-2a) ^ 2 + \ frac {p-1} 4 \ cdot (p-2b) ^ 2 = p ^ 3 + 2 (p-1) (a ^ 2 + b ^ 2)$

N की गणना करने की दूसरी विधि में , पहले x ₁ और x _{2 को} ठीक करें और तीनों t और y की संख्या की गणना करें, जिसके बाद हम सभी जोड़े x के लिए परिणाम जोड़ते हैं। X ₁ = x ₂ = 0̅ के लिए बिल्कुल p विकल्प हैं: दोनों y को शून्य होना चाहिए, t कोई भी हो सकता है। X ₁ = 0 x और नॉनज़रो x _{2 के लिए यह} y ₁ = 0 होना चाहिए, y ₂ कोई भी हो सकता है, t की गणना असंदिग्ध रूप से की जाती है, p विकल्प फिर से प्राप्त होते हैं। शून्य x ₂ और गैर-शून्य x _{1 के साथ स्थिति} सममित है। अंत में, दोनों x को नॉनज़रो होने दें। फिर t = x ₁ ² - (y ₁ ² / x ₁ ) और आपको शर्त (x ₂ / x ₁ ) y ₁ ² = y ² + x ₂ (x ₁ ² -x ₂ ² ) के साथ युग्म y की संख्या की गणना करने की आवश्यकता है।

यदि x ₁ = x ₂ , तो समीकरण y के वर्गों के लिए एक स्थिति में बदल जाता है, और y के विभिन्न जोड़े 1 + 2 (p-1) प्राप्त करते हैं : प्रत्येक गैर-शून्य y _{1 के} लिए शून्य और दो विकल्प y ₂ । यदि x ₁ = -x ₂ , स्थिति समान है, क्योंकि p शेष 1 देता है जब 4 और -1̅ से विभाजित किया जाता है चतुर्भुज अवशेष।

यदि x ₂ / x ₁ एक द्विघात अवशेष है जो ̅ 1 then के बराबर नहीं है, तो कुछ नॉनजरो c है जैसे कि c ² = x ₂ / x ₁ । तब (c ² y ₁ ² -y ₂ ² ) = (c-y ₁ -y ₂ ) (c ₂ y ₁ + y ₂ ) = x ₂ (x ₁ ² -x ₂ ² ) , अभिव्यक्ति c ₁ y ₁ - y ₂ कोई भी नॉनवेज अवशेष हो सकता है, यह विशिष्ट रूप से ∙ y ₁ + y ₂ और इसलिए, y ₁ और y ₂ निर्धारित करता है। कुल पी -1 विकल्प।

यदि x ₂ / x ₁ एक द्विघात गैर-अवशेष है, तो, इसी तरह अण्डाकार वक्रों के लिए, समाधानों की संख्या द्विभुज अवशेषों के मामले में समाधानों की संख्या 2p है , अर्थात 2p- (p-1) = p + 1 ।

सारांश बनाएं। एक्स ₁ = एक्स ₂ = 0 के साथ एक विकल्प है पी समाधान दे रहा है। 2 (p-1) विकल्प हैं, जहां x में से एक शून्य है और दूसरा गैर-शून्य है, प्रत्येक विकल्प p समाधान देता है। X ₂ = , x _{1 के} साथ 2 (p-1) विकल्प हैं, जिनमें से प्रत्येक 2p-1 समाधान देता है। वहाँ (पी -1) ((पी -1) / 2-2) विकल्प हैं, जहां एक्स ₁ एक मनमाना नॉनवेज अवशेष है, और x ₂ / x ₁ ̅ ₁ quad के अलावा एक द्विघात अवशेष है, इन विकल्पों में से प्रत्येक पी -1 है समाधान। अंत में, (p-1) ^2/2 विकल्प हैं, जहां x ₁ एक मनमाना गैर-अवशेष अवशेष है और x ₂ / x ₁ एक द्विघात गैर-अवशेष है, इनमें से प्रत्येक विकल्प में p + 1 समाधान हैं। कुल मिलाकर 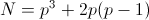एन = पी ^ 3 + 2 पी (पी -1)

।

एन के लिए दो अभिव्यक्तियों की तुलना प्रमाण को पूरा करती है।

और क्रिप्टोग्राफी के बारे में क्या?

पी बार लीजेंड्रे प्रतीकों की गणना करके ए और बी की गणना करना अव्यावहारिक है। Cornacchia एल्गोरिथ्म इसे बहुत तेजी से संभाल सकता है । व्यावहारिक लाभ यह है कि विपरीत दिशा में a, b के लिए सूत्र का उपयोग करें: यह साबित किया जा सकता है कि विस्तार p = a ² + b ² , a और b और संकेतों के परिवर्तन के लिए अप करने के लिए अद्वितीय है, इसलिए a और b का पता लगाना घटता y पर बिंदुओं की संख्या ज्ञात करता है। ² = x ³ -t for x किसी भी नॉनजरो टी के लिए , यह p + 1 a 2a और p + 1 + 2b होगा ।

वक्र पर क्रिप्टोग्राफी के लिए किसी वक्र पर बिंदुओं की संख्या जानना महत्वपूर्ण है। अण्डाकार वक्र पर, आप बिंदुओं के संचालन में प्रवेश कर सकते हैं (जो कि शायद हर किसी के द्वारा सुना जाता है जो क्रिप्टोग्राफी के बारे में कम से कम कुछ जानते हैं) शून्य की भूमिका में एक विशेष बिंदु ओ के साथ। इसके अलावा ऑपरेशन के आधार पर, एक प्राकृतिक संख्या से गुणा निर्धारित किया जा सकता है: 2P = P + P , 3P = P + P + P, और इसी तरह। तो, हम यह साबित कर सकते हैं कि यदि n वक्र का क्रम है, तो nP = O किसी बिंदु P के लिए । N, c, d , को जानकर , प्रपत्र x c (cP) के समीकरणों को हल कर सकते हैं = dP पूरी तरह से अवशेषों के विभाजन के अनुरूप है: उन्नत यूक्लिडियन एल्गोरिथ्म x, y को ऐसे c + x + n ∙ y = 1 , whence x x (cP) + के रूप में जानता है। y y (nP) = P , अर्थात, x c (cP ) = P। इसके अलावा, यदि c, d अज्ञात हैं, और cP और dP निर्देशांक द्वारा दिए गए हैं, तो प्रभावी विभाजन विधियां आमतौर पर अज्ञात हैं।

किसी दिए गए वक्र पर बिंदुओं की संख्या की गणना करना मुश्किल है (एक बहुपद एल्गोरिथ्म मौजूद है, लेकिन व्यवहार में धीमी है)। अंकों की संख्या पर कुछ गुणों के साथ एक वक्र बनाने के लिए, आप यादृच्छिक गुणांक लेने की कोशिश कर सकते हैं और चक्र में बिंदुओं की संख्या की गणना तब तक कर सकते हैं जब तक आपको वह नहीं मिल जाता है जो आपको चाहिए, लेकिन आपको इंतजार करना होगा। सौभाग्य से, एक और तरीका है।

यदि हम फॉर्म 4k + 1 की एक प्रमुख संख्या और एक विशेष फॉर्म y ² = x ³ -t sense x (एक अर्थ में, यह किसी भी नॉनजरो टी के लिए एक ही वक्र है ) अंक p + 1 k 2a या p + 1 ± की संख्या से संतुष्ट हैं। 2 बी , आप इसे ले सकते हैं। अन्य घटता के बारे में क्या?

थोड़ी देर बाद, 1911 में, एक अन्य लेखक वॉन श्रुतका ने फॉर्म y ² = x ³ -t के कर्व्स, 6k + 1 के सरल रूप, और प्रतिनिधित्व p = एक ² + 3b ^{2 के} समान परिणाम प्राप्त किया । तो, वक्र y ² = x ³ -t पर बिंदुओं की संख्या को खोजने के लिए , फिर से, कॉर्नचिया एल्गोरिथ्म की अनुमति देता है।

प्रमाण के बारे में कुछ शब्द

एक पूरे के रूप में प्रमाण उपरोक्त के समान है, केवल तीन संख्या a, b ₁ , b ₂ t = 1, g ² , g ^{4 के} लिए दिखाई देते हैं, जहाँ g एक घन नहीं है, उनका योग शून्य है, और वर्गों का योग की गणना की जाती है। सरल परिवर्तनों के बाद, हमें वह मिलता है, जिसकी हमें आवश्यकता होती है।

बाद में, जैसे कि अण्डाकार वक्रों का सिद्धांत विकसित हुआ, यह स्पष्ट हो गया कि यदि कुछ प्रतिनिधित्व 4p = a ' ² + d + b' ^{2 है} , जहाँ d प्राकृतिक है, जब 4 से विभाजित किया जाता है, तो यह शेष 0 या 3 देता है, जो p के लिए सहानुभूति है और नहीं बहुत बड़ा है, यह कुशलतापूर्वक संभव है (भले ही पी बहुत बड़ा हो) एक वक्र का निर्माण करता है जिसमें बिल्कुल p + 1 points ' अंक होंगे। दो सबसे छोटे मान d = 3 और d = 4 घटता y ² = x ³ -t और y ² = x ³ -t-x के अनुरूप हैं। उदाहरण के लिए d = 163 :
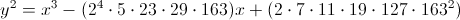
$y ^ 2 = x ^ 3- (2 ^ 4 \ cdot5 \ cdot23 \ cdot29 \ cdot163) x + (2 \ cdot7 \ cdot11 \ cdot19 \ cdot127 \ cdot163) 2 + 2$
विषम p odd 163 के लिए, यह समीकरण एक अण्डाकार वक्र को परिभाषित करता है। यदि 4p को ' ² + 163b' ² के रूप में पूर्णांक 'a, b' के रूप में दर्शाया जा सकता है , तो दीर्घवृत्त वक्र पर बिंदुओं की संख्या p + 1 ± a 'है । यदि नहीं, तो p + १ । दुर्भाग्य से, प्रमाण एक "कठिन" सिद्धांत का उपयोग करता है, इसलिए यहां कोई संकेत भी नहीं होगा।
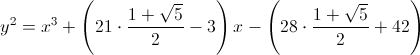
आमतौर पर, हालांकि, कट्टरपंथी प्राप्त किए जाएंगे। उदाहरण के लिए, d = 15 के लिए : $y ^ 2 = x ^ 3 + \ left (21 \ cdot \ frac {1+ \ sqrt5} {2} -3 \ right) x- \ left (28 \ cdot \ frac {1+ \ sqrt5} {2} + 42 \ _)$ । यदि 4p योग ' ² + d ² b' ² में घटता है और p , d के साथ सहवर्ती होता है, तो सभी मूलक अनिवार्य रूप से निकाले जाते हैं (उदाहरण के लिए, d = 15 के लिए हमेशा एक ग c होता है , जिसके लिए c ^{2 /} 5̅ ) और हमें एक दीर्घवृत्त वक्र प्राप्त होता है। अंकों की वांछित संख्या।

दो वर्गों और अण्डाकार वक्रों के योग से संख्याओं का प्रतिनिधित्व

कटौती

अंडाकार घटता के बारे में थोड़ा सा

द्विघात कटौती और गैर-कटौती

सबूत

और क्रिप्टोग्राफी के बारे में क्या?

More articles: