अण्डाकार क्रिप्टोग्राफी: अभ्यास

हाय% उपयोगकर्ता नाम%!

कुछ हफ़्ते पहले मैंने एलिप्टिक क्रिप्टोग्राफ़ी: ए थ्योरी पर एक पोस्ट प्रकाशित की थी जिसमें मैंने क्रिप्टोग्राफी में अण्डाकार वक्रों का उपयोग करने के मुख्य पहलुओं का वर्णन करने की कोशिश की थी। मेरा यह पद केवल सूचनात्मक उद्देश्यों के लिए था, और संकलक के साथ किसी अन्य काम के लिए उपलब्ध नहीं था, केवल चिंतन को छोड़कर। लेकिन अभ्यास के बिना एक सिद्धांत क्या है? इस चूक को ठीक करने के लिए, मैंने, अपने आप को लांघते हुए, GOST 34.10-2012 के साथ युद्ध में भाग लिया, अंडाकार घटता पर ईडीएस योजना। यदि आप यह देखना चाहते हैं कि यह सब क्या हुआ, तो बिल्ली का स्वागत करें।

अण्डाकार वक्र चयन

आपको याद दिला दूं कि अण्डाकार क्रिप्टोग्राफी में तथाकथित "एक परिमित क्षेत्र में घटता है।" इसका मतलब यह है कि वक्रों के पास सीमित संख्या में बिंदु हैं। ऐसे वक्र के बिंदुओं की संख्या को वक्र का क्रम कहा जाता है । क्रिप्टोग्राफी में एक अण्डाकार वक्र का उपयोग करने के लिए, आपको इसका क्रम जानना होगा। यह कम से कम इस तथ्य के कारण है कि सिस्टम की क्रिप्टोग्राफिक ताकत वक्र के आदेश पर निर्भर करती है, जैसा कि मैंने अपने पिछले टोट्स में लिखा था।
यह वह जगह है जहां सभी जटिलता निहित है। वक्र चयन प्रक्रिया निम्नानुसार लिखी जा सकती है:

1. रेखा के समीकरण का वर्णन करने वाले a और b के मापदंडों का चुनाव
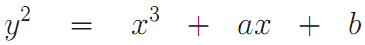
2. चयनित वक्र के गिनती अंक;
3. यह जांचता है कि किसी दिए गए अंक के साथ चयनित वक्र कई स्थितियों से मेल खाता है या नहीं।

तो, समस्या यह है कि अण्डाकार वक्र के क्रम की गणना करना एक बहुत ही गैर-तुच्छ कार्य है।

अंकों की संख्या की गणना के लिए सबसे आम तरीका है , Schuf एल्गोरिथ्म। । इसके अलावा, एल्गोरिथ्म बहुत ही गंभीर गणितीय तरीकों का उपयोग करता है और इसे समझना बहुत मुश्किल है।

एक और तरीका है, तथाकथित जटिल गुणन विधि । अच्छे हरबेरमैन ग्रेचनिक ने दो चौकों और अण्डाकार वक्रों के योग द्वारा इस पद्धति के बारे में जानकारी अपने पोस्ट प्रतिनिधि संख्या में साझा की। संक्षेप में, यह विधि दी गई संख्याओं के साथ घटता को खोजने के लिए इसे और अधिक कुशल बनाती है। हालांकि, Schuf एल्गोरिथ्म के विपरीत, जो सार्वभौमिक है, जटिल गुणन की विधि केवल तभी काम करती है यदि कुछ शर्तों को पूरा किया जाता है। यह विधि भी इतनी सरल नहीं है जितनी पहली बार में लग सकती है। आप यहां इसके बारे में अधिक पढ़ सकते हैं , उदाहरण के लिए (लिंक के लिए धन्यवाद, grechnik )।

जाहिर है, डेवलपर्स के लिए जीवन को आसान बनाने के लिए बैकस्ट बनाने के लिए NIST का लाभ, एक ज्ञात संख्या के साथ अण्डाकार वक्रों की एक सूची है जो EDS योजनाओं में उपयोग के लिए अनुशंसित हैं। वास्तव में, मैंने अपने प्रयोगों के लिए इनमें से एक वक्र चुना।

वक्र का वर्णन करने के लिए, NIST मानक 6 पैरामीटर D = (p, a, b, G, n, h) के सेट का उपयोग करता है, जहां

पी एक प्रधान है, अण्डाकार वक्र का मापांक है;
ए, बी - अण्डाकार वक्र का समीकरण सेट करें ;
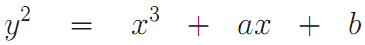
जी एक बड़े क्रम के अण्डाकार वक्र का एक बिंदु है। इसका मतलब यह है कि यदि आप बिंदु के क्रम से छोटे से एक अंक गुणा करते हैं, तो हर बार पूरी तरह से अलग-अलग अंक प्राप्त किए जाएंगे;
n बिंदु G का क्रम है;
h एक पैरामीटर है जिसे कॉफ़ेक्टर कहा जाता है। यह अण्डाकार वक्र पर बिंदु जी के आदेश की कुल संख्या के अनुपात से निर्धारित होता है। यह संख्या यथासंभव छोटी होनी चाहिए।

मापदंडों के बारे में कुछ शब्द

वास्तव में पसंद के साथ परेशान नहीं, मैंने पहले अनुशंसित एनआईएसटी वक्र का उपयोग करने का फैसला किया, जिसमें ऊपर वर्णित मापदंडों का मूल्य क्रमशः है:
p = 6277101735386680763835789423207666416083908700390324961279;
a = -3;
b = 2455155546008943817740293915197451784769108058161191231165;
x _G = 602046282375688656758213480587526111916698976636884684818 (बिंदु G का समन्वय);
y _G = १75४०३२३२२३२२३२२३२१५२५५५५५२२२०२१ ९ ४१०३६३०२३४88४9 ९ २64३६६६६६१ (बिंदु G का समन्वय);
n = 6277101735386680763835789423176059013767194773182842284081;
ज = १।

मुझे आपको पैरामीटर p के बारे में अधिक बताना चाहिए। यह संख्या सामान्यीकृत मेर्सेन संख्या को संदर्भित करती है, जिसका अर्थ है कि इसे दो की विभिन्न शक्तियों के योग के रूप में दर्शाया जा सकता है। विशेष रूप से, हमारे मामले में, संख्या पी के रूप में लिखा जा सकता है
p = 2 ¹⁹² -2 ⁶⁴ -1।
NIST द्वारा अनुशंसित मुख्य क्षेत्र के ऊपर सभी अण्डाकार वक्र इस तरह से लिखे जा सकते हैं। ऐसी संख्याओं का उपयोग आपको बड़ी संख्या में गुणा मोडुलो के संचालन में तेजी लाने की अनुमति देता है। विधि का सार मशीन के शब्दों के रूप में गुणन के परिणाम को 32 बिट लंबा पेश करना है, जिसके संयोजन से वांछित उत्पाद मोडुलो में बड़ी संख्या में परिणाम होता है। आप इसके बारे में अधिक पढ़ सकते हैं, उदाहरण के लिए, यहां (टिप के लिए धन्यवाद डेटाकंपबॉय )।

एक और दिलचस्प बिंदु बिंदुओं के निर्देशांक से संबंधित है। अक्सर, विभिन्न प्रकार की विशिष्टताओं में, अण्डाकार वक्र का जनन बिंदु जी एक संपीड़ित रूप में निर्दिष्ट होता है। उदाहरण के लिए, हमारे मामले में, बिंदु G को निम्नानुसार परिभाषित किया जा सकता है:

G = 0x 03 188da80eb03090f67cbf20eb43a18800f4ff0afdffff282

पहला बाइट डेटा को y- समन्वय की समता पर संग्रहीत करता है। यह 2 के बराबर हो सकता है (इसका अर्थ है कि y- समन्वय सम है) या 3 (क्रमशः, विषम)। शेष बाइट्स एक्स-समन्वय की दुकान करते हैं।
इस डेटा के बाद, हम निम्नानुसार y- समन्वय को पुनर्स्थापित कर सकते हैं।

हम जानते हैं कि बिंदु G एक अण्डाकार वक्र से संबंधित है। तदनुसार, समानता इसके लिए रखती है:



और हम y की गणना कर सकते हैं:

।

चूँकि वर्गाकार रूट मोडुलो पी की गणना दो संख्या y और py है , हम उस संख्या को चुनते हैं जिसकी समता निर्देशांक जी के संपीडित रिकॉर्ड की पहली बाइट की समता से मेल खाती है।

हस्ताक्षर का गठन

ईडीएस एल्गोरिथ्म के कार्यान्वयन के साथ आगे बढ़ने से पहले, एक दीर्घवृत्त वक्र के बिंदुओं के साथ काम करने के लिए एक वर्ग लिखना आवश्यक है। मैंने गणितीय कानूनों और पिछले पोस्ट में अण्डाकार वक्रों पर संचालन के बारे में थोड़ा लिखा था, इसलिए मैं अब इस पर ध्यान केंद्रित नहीं करूंगा।
मैं केवल यह कह सकता हूं कि GOST 34.10 के कार्यान्वयन के लिए हमें केवल तीन कार्यों की आवश्यकता होगी:

• दो अलग-अलग बिंदुओं का जोड़;
• संदेह का बिंदु
• एक बिंदु की संख्या से गुणा करना।

उदाहरण के लिए, आप विकिपीडिया पर कुछ और विवरण पा सकते हैं।

ECPoint वर्ग के कार्यान्वयन को देखें जो आपको स्पॉइलर के तहत इन क्रियाओं को करने की अनुमति देता है।



डिजिटल हस्ताक्षर बनाने के लिए, बड़ी संख्या में d का उपयोग किया जाता है , जो कि योजना की स्थायी गुप्त कुंजी है , और केवल हस्ताक्षरकर्ता को पता होना चाहिए।
GOST एल्गोरिथ्म के अनुसार संदेश M के हस्ताक्षर की गणना करने के लिए, निम्नलिखित चरणों का पालन करना चाहिए:

1. संदेश हैश M: H = h (M) की गणना करें। इस चरण में, हैश फ़ंक्शन स्ट्रिबॉग का उपयोग किया जाता है, जिसके बारे में मैंने पहले ही हैबे पर लिखा था ;
2. एक पूर्णांक α की गणना करें जिसका द्विआधारी प्रतिनिधित्व एच है;
3. ई = α मॉड एन निर्धारित करें, यदि ई = 0, सेट ई = 1;
4. एक यादृच्छिक संख्या कश्मीर उत्पन्न करें स्थिति को संतोषजनक 0 <k <n;
5. अण्डाकार वक्र C = k * G के बिंदु की गणना करें;
6. निर्धारित करें कि आर = एक्स _सी मॉड एन, जहां एक्स _सी बिंदु सी का एक्स-समन्वय है। यदि आर = 0 है, तो चरण 4 पर लौटें;
7. मान s = (rd + ke) mod n की गणना करें। यदि s = 0 है, तो चरण 4 पर लौटें;
8. डिजिटल हस्ताक्षर के रूप में r का मान लौटाएं।

हम एक SignGen फ़ंक्शन लिखेंगे जो इन सभी कार्यों को लागू करता है:

  public string SignGen(byte[] h, BigInteger d) { BigInteger alpha = new BigInteger(h); BigInteger e = alpha % n; if (e == 0) e = 1; BigInteger k = new BigInteger(); ECPoint C=new ECPoint(); BigInteger r=new BigInteger(); BigInteger s = new BigInteger(); do { do { k.genRandomBits(n.bitCount(), new Random()); } while ((k < 0) || (k > n)); C = ECPoint.multiply(k, G); r = Cx % n; s = ((r * d) + (k * e)) % n; } while ((r == 0)||(s==0)); string Rvector = padding(r.ToHexString(),n.bitCount()/4); string Svector = padding(s.ToHexString(), n.bitCount() / 4); return Rvector + Svector; } 

कोड के उद्धृत भाग में, पैडिंग फ़ंक्शन मॉड्यूल पी की लंबाई के लिए आर और एस की संख्या के हेक्साडेसिमल अभ्यावेदन का पूरक है, ताकि हस्ताक्षर की जांच करते समय वे पार्स हो सकें।

हस्ताक्षर का सत्यापन

हस्ताक्षर को सत्यापित करने के लिए, एक बिंदु क्यू का उपयोग किया जाता है जो समानता को संतुष्ट करता है क्यू = डी * जी। प्वाइंट क्यू सर्किट की सार्वजनिक कुंजी है और इसे किसी भी समीक्षक के लिए जाना जा सकता है।
हस्ताक्षर सत्यापन प्रक्रिया निम्न एल्गोरिथम के अनुसार होती है:

1. प्राप्त हस्ताक्षर का उपयोग करते हुए, आर और एस संख्या बहाल करें। यदि असमानताएं 0 <r <n और 0 <s <n संतुष्ट नहीं हैं, तो "हस्ताक्षर सत्य नहीं है" लौटें;
2. संदेश की गणना करें हैश M: H = h (M);
3. एक पूर्णांक α की गणना करें जिसका द्विआधारी प्रतिनिधित्व एच है;
4. ई = α मॉड एन निर्धारित करें, यदि ई = 0, सेट ई = 1;
5. वी = ई ^-1 मॉड एन की गणना करें;
6. मानों की गणना करें z ₁ = s * v mod n और z ₂ = -r * v mod n;
7. अण्डाकार वक्र C = z ₁ * G + z ₂ * Q के बिंदु की गणना करें;
8. निर्धारित करें R = x _c mod n, जहाँ x _c बिंदु C का x-निर्देशांक है;
9. यदि R = r, तो हस्ताक्षर सही है। अन्यथा, हस्ताक्षर स्वीकार नहीं किया जाता है।

यह समझने के लिए कि यह क्यों काम करता है, हम सूत्र के रूप में हस्ताक्षर सत्यापन प्रक्रिया लिखते हैं:

जैसा कि आप देख सकते हैं, सत्यापन चरण में हमें बहुत ही बिंदु C = k * G मिलता है, जो हस्ताक्षर बनाते समय समान होता है।

SignVer फ़ंक्शन प्रदर्शन सत्यापन:

  public bool SignVer(byte[] H, string sign, ECPoint Q) { string Rvector = sign.Substring(0, n.bitCount() / 4); string Svector = sign.Substring(n.bitCount() / 4, n.bitCount() / 4); BigInteger r = new BigInteger(Rvector, 16); BigInteger s = new BigInteger(Svector, 16); if ((r < 1) || (r > (n - 1)) || (s < 1) || (s > (n - 1))) return false; BigInteger alpha = new BigInteger(H); BigInteger e = alpha % n; if (e == 0) e = 1; BigInteger v = e.modInverse(n); BigInteger z1 = (s * v) % n; BigInteger z2 = n + ((-(r * v)) % n); this.G = GDecompression(); ECPoint A = ECPoint.multiply(z1, G); ECPoint B = ECPoint.multiply(z2, Q); ECPoint C = A + B; BigInteger R = Cx % n; if (R == r) return true; else return false; } 

GDecompression () फ़ंक्शन " अनपैकिंग " बिंदुओं का प्रदर्शन करता है।

DSGost वर्ग, जो GOST 34.10-2012 एल्गोरिथम के अनुसार संदेशों के हस्ताक्षर और सत्यापन को लागू करता है, को स्पॉइलर के नीचे देखा जा सकता है।


एक वर्ग के साथ काम करने का एक उदाहरण:

  private void ECTest() { BigInteger p = new BigInteger("6277101735386680763835789423207666416083908700390324961279", 10); BigInteger a = new BigInteger("-3", 10); BigInteger b = new BigInteger("64210519e59c80e70fa7e9ab72243049feb8deecc146b9b1", 16); byte[] xG = FromHexStringToByte("03188da80eb03090f67cbf20eb43a18800f4ff0afd82ff1012"); BigInteger n = new BigInteger("ffffffffffffffffffffffff99def836146bc9b1b4d22831", 16); DSGost DS = new DSGost(p, a, b, n, xG); BigInteger d=DS.GenPrivateKey(192); ECPoint Q = DS.GenPublicKey(d); GOST hash = new GOST(256); byte[] H = hash.GetHash(Encoding.Default.GetBytes("Message")); string sign = DS.SignGen(H, d); bool result = DS.SignVer(H, sign, Q); } 

निष्कर्ष

हमने मामले की जांच की जब क्रिप्टोसिस्टम को अवशेष फ़ील्ड मॉडुलो के ऊपर एक अण्डाकार वक्र पर बनाया गया है जो एक बड़ी अभाज्य संख्या है। हालांकि, हमें यह नहीं भूलना चाहिए कि अण्डाकार क्रिप्टोग्राफी की अवधारणा इस विशेष मामले की तुलना में बहुत अधिक शामिल है। और जब अन्य प्रकार के क्षेत्रों पर अण्डाकार वक्रों पर क्रिप्टोकरंसी को लागू करते हैं, तो यह ध्यान रखना आवश्यक है कि इन वक्रों पर गणितीय संचालन इस पोस्ट में प्रस्तुत किए गए लोगों से काफी भिन्न हो सकते हैं।

पुनश्च परियोजना स्रोत यहाँ हैं ।

संदर्भ

1. मानक GOST 34.10-2012 का संदर्भ;
2. अनुशंसित घटता की सूची के साथ ECDSA मानक से लिंक करें।
3. कुशल क्रिप्टोग्राफी के लिए मानक, अनुशंसित वक्रों की एक विस्तारित सूची।