पिछले
लेख में, मैंने खोज को अनुकूलित करने के लिए अनुमानी तरीकों के बारे में लिखा था। इस लेख में मैं आपको एक और के बारे में बताऊंगा, लेकिन पहले से ही स्पर्शोन्मुख अनुकूलन - मीट-इन-बीच।
इस विधि के लिए विशिष्ट स्पर्शोन्मुख कमी विधि हैं:

और

।
प्रविष्टि
विधि यह है कि कार्य को आधा में विभाजित करें, कुछ डेटा प्राप्त करें और एक दूसरे के साथ उनकी तुलना करें।
किसी विशेष कार्य के लिए दो शर्तें पूरी होने पर, बीच-बीच में मिलना मायने रखता है:
1) अंतिम उत्तर प्राप्त करने के समय की तुलना में आधे डेटा का प्रसंस्करण समय असमान रूप से कम है।
2) इसके हिस्सों के प्रसंस्करण के बारे में जानकारी का उपयोग करके पूरी समस्या का उत्तर पाने के लिए एक विषम रूप से तेज़ तरीका है।
समझने के लिए, उदाहरणों को देखना सबसे अच्छा है (बढ़ती जटिलता के क्रम में दिए गए):
उदाहरण # 1: गणना अनुकूलन
N नंबर दिए। के नंबरों को चुनना आवश्यक है ताकि उनकी राशि 0 के बराबर हो (समान तत्वों का कई बार उपयोग किया जा सकता है)।
Naive solution:
सभी के माध्यम से जाओ
 k
k नंबरों के विकल्प, पुनरावर्तन के दौरान राशि का पुनरावर्तन। Asymptotics:
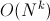
।
मी-इन-बीच के समाधान के लिए भी
k :
1) मानसिक रूप से
k संख्याओं को दो /
k / 2 के बवासीर में विभाजित करें।
२.१) हम सब कुछ लिखते हैं

बराबर है।
२.२) सॉम्स की सरणी को क्रमबद्ध करें।
2.3) प्रत्येक राशि के लिए हम एक द्विआधारी खोज के साथ खोजने की कोशिश करते हैं।
२.४) यदि आप पाते हैं, तो यहाँ है, हमारा उत्तर। यदि नहीं, तो ऐसा संयोजन मौजूद नहीं है।
3) लाभ:

।
विषम
कश्मीर के लिए इस एल्गोरिथ्म को बदलना, मुझे लगता है, आपके लिए मुश्किल नहीं होगा।
यदि
एन = 30, और
के = 12, तो मीट-इन-बीच लगभग एक मिनट के लिए काम करेगा, और भोली एल्गोरिथ्म 17 साल तक चलेगा।
उदाहरण नंबर 2: राज्यों के एक विशाल ग्राफ में सबसे छोटे रास्ते की खोज का अनुकूलन
जादूगर के पास 36 ताश के पत्तों का एक डेक है। प्रारंभ में, वे क्रम 1, 2, 3 ... में हैं, और वह कुछ विशिष्ट क्रमपरिवर्तन प्राप्त करना चाहते हैं, और
k कदमों से अधिक नहीं। प्रत्येक चरण पर, जादूगर डेक की शुरुआत में लगातार कार्ड बदलता है।
चुनौती यह पता लगाने की है कि क्या उसे वांछित क्रमोन्नति मिल सकती है।
हम राज्य ग्राफ
एस को एक ग्राफ के रूप में परिभाषित करते हैं जिसमें नक्शे के वर्तमान क्रमांकन द्वारा कोने को परिभाषित किया जाता है, और किनारों को 1 चरण में एक क्रमांकन से दूसरे में जाने की क्षमता होती है। यह ध्यान देने योग्य है कि इस कॉलम में ३६!

कोने, लेकिन प्रत्येक शीर्ष से 36-
मी +1 छोर है, जो अपेक्षाकृत छोटा है।
Naive solution:
राज्य ग्राफ
एस पर एक चौड़ाई-पहली खोज चलाएँ
। यदि आप
k +1 पर वांछित स्थिति या शीर्ष रिमोट तक पहुंचते हैं, तो खोज को पूरा करें। Asymptotics:

।
मीट-इन-द-मिडिल के साथ समाधान:
1) के / 2 की अधिकतम गहराई के साथ प्रारंभ और अंत के कोने से दो चौड़ाई खोजें चलाएँ। हम दो सेट लिखते हैं: सभी राज्य जिसमें पहली-पहली खोजों का दौरा किया।
2) यदि ये सेट प्रतिच्छेद करते हैं, तो एक रास्ता है, यदि नहीं, तो कोई रास्ता नहीं है।
3) लाभ:
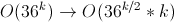
।
उदाहरण संख्या 3: "अच्छे" सबसेट की संख्या की गिनती
ऑलिम्पीडनिकोव और उन लोगों के लिए जो एक मस्तिष्क को तोड़ना चाहते हैंएक ग्राफ
जी (
एन कोने) दिया। कॉलम
जी (क्लिक) के पूर्ण उपग्रहों की संख्या को गिनना आवश्यक है।
Naive solution:
सभी के माध्यम से जाओ

सबग्राफ और वर्ग के लिए जाँच करें कि यह एक क्लिक है। Asymptotics:

।
इस एल्गोरिथ्म में सुधार किया जा सकता है

। ऐसा करने के लिए, आपको पुनरावर्ती खोज फ़ंक्शन में कोने का एक मुखौटा संग्रहीत करने की आवश्यकता है, जिसे हम अभी भी जोड़
सकते हैं। इस मास्क का समर्थन करके, आप केवल "आवश्यक" वर्टिकल जोड़ सकते हैं, और फिर, अंत में, आपको इस तथ्य के लिए सबग्राफ की जांच करने की आवश्यकता नहीं होगी कि यह एक क्लिक है। आप के लिए एक शीर्ष जोड़ सकते हैं
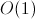
वर्तमान मास्क और जोड़े गए शीर्ष के आसन्न मैट्रिक्स पंक्ति के बिटवाइज़ "और" का उपयोग करना।
मीट-इन-द-मिडिल के साथ समाधान।
१.१) हम ग्राफ को
G को २ ग्राफ
G1 और
G2 में
N / २ कोने में विभाजित करते हैं। हम ढूंढते हैं

उनमें से प्रत्येक में सभी क्लिक। Asymptotics:

।
अब हमें ग्राफ
G1 के प्रत्येक क्लिक पर ग्राफ
G2 के क्लिकों की संख्या का पता लगाने की आवश्यकता है, जैसे कि उनका संघ एक क्लिक है। उनका योग अंतिम उत्तर है।
चूंकि ग्राफ
G1 के एक क्लिक
K के लिए G2 में कई उपयुक्त क्लिक्स हो सकते हैं, इसलिए पिछले दो उदाहरणों में उसी विधि का उपयोग करना विफल हो जाएगा। लेकिन क्ले
K के लिए एकमात्र वस्तु ग्राफ
G2 के शीर्षों का मुखौटा है, जिसे अभी भी जोड़ा जा सकता है। हमारे पास पूर्व-गणना के लिए बहुत समय है और हमें इसका उपयोग करने की आवश्यकता है:
जी 2 में ऐसे प्रत्येक मुखौटा के लिए आपको उत्तर की गणना करने की आवश्यकता है, अर्थात्:
1.2) गतिशील प्रोग्रामिंग विधि का उपयोग करते हुए, ग्राफ
G2 के कोने के प्रत्येक मुखौटा के लिए
हम उन क्लिक्स की संख्या की गणना करते हैं जिनके कोने चयनित मास्क का सबसेट हैं। राज्यों की संख्या:

। संक्रमण की संख्या:

। Asymptotics:

।
यहाँ पायथन में एक बयान है:
for mask in range(1 << N): dp[mask] = 1 + sum([dp[mask & matrix[i]] for i in range(N) if ((mask & (1 << i)) > 0)])
2) ग्राफ
G1 के प्रत्येक क्लिक
K (खाली वाले सहित) के लिए
, हम वैश्विक प्रतिक्रिया में क्लिकों की गणना की गई संख्या को जोड़ते हैं जिन्हें
K (खाली वाले सहित) में जोड़ा जा सकता है। Asymptotics:

।
3) लाभ:

।
निष्कर्ष
मुझे आशा है कि मैं मीट-इन-बीच की अवधारणा को स्पष्ट रूप से समझाने में सक्षम था। यदि आपके कोई प्रश्न हैं, तो टिप्पणियों में पूछें, मैं उत्तर देने का प्रयास करूंगा। आपका ध्यान देने के लिए धन्यवाद।