रीड-सोलोमन कोड। सरल उदाहरण है

रीड-सोलोमन कोड के लिए धन्यवाद, आप बहुत सी खरोंच के साथ एक सीडी पढ़ सकते हैं, या बहुत अधिक हस्तक्षेप के साथ संचार की स्थिति में जानकारी संचारित कर सकते हैं। सीडी के लिए औसतन, कोड अतिरेक (यानी अतिरिक्त वर्णों की संख्या जो जानकारी को पुनर्प्राप्त करने के लिए उपयोग की जा सकती है) लगभग 25% है। इस मामले में, आप आधे निरर्थक के बराबर डेटा की मात्रा को पुनर्स्थापित कर सकते हैं। यदि डिस्क क्षमता 700 एमबी है, तो, यह निकलता है, सैद्धांतिक रूप से 700 से 87.5 एमबी तक पुनर्स्थापित करना संभव है। साथ ही, हमें यह जानने की जरूरत नहीं है कि कौन सा प्रतीक एक त्रुटि के साथ प्रेषित किया गया था। यह भी ध्यान देने योग्य है कि कोडिंग के साथ इंटरलाकिंग का उपयोग किया जाता है, जब विभिन्न ब्लॉकों के बाइट्स को एक निश्चित क्रम में मिश्रित किया जाता है, जिसके परिणामस्वरूप आप एक दूसरे के करीब स्थानीयकृत नुकसान के साथ डिस्क को पढ़ने की अनुमति देते हैं (उदाहरण के लिए, गहरी खरोंच, क्योंकि ऑपरेशन के बाद, रिवर्स इंटरलेइंग। मरम्मत के कई ब्लॉकों में एकल त्रुटियों में व्यापक क्षति होती है जिसे मरम्मत किया जा सकता है।

चलो एक सरल उदाहरण लेते हैं और सभी तरह से जाने की कोशिश करते हैं - कोडिंग से लेकर रिसीवर तक स्रोत डेटा प्राप्त करने तक। मान लीजिए हमें एक कोडवर्ड सी पास करने की आवश्यकता है जिसमें दो संख्याएँ हैं - 3 और 1 बिल्कुल इसी क्रम में, अर्थात्। हमें वेक्टर C = (3,1) को स्थानांतरित करने की आवश्यकता है। मान लीजिए कि हम अधिकतम दो त्रुटियों को ठीक करना चाहते हैं, यह जानते हुए भी नहीं कि वे कहां दिखाई दे सकती हैं। ऐसा करने के लिए, 2 * 2 = 4 निरर्थक अक्षर लें। हम उन्हें अपने शब्द में शून्य के साथ लिखते हैं, अर्थात्। C अब (3,1,0,0,0,0) के बराबर है। अगला, आपको गणितीय विशेषताओं के बारे में थोड़ा समझने की आवश्यकता है।

फ़ील्ड्स गैलोज़

बहुत से लोग एक युवक की रोमांटिक कहानी जानते हैं, जो केवल 20 साल तक रहता था और एक रात ने अपना गणितीय सिद्धांत लिखा था, और सुबह एक द्वंद्व में मारा गया था। यह एवेरिस्ट गैलोज है । उन्होंने कई बार विश्वविद्यालयों में प्रवेश करने की भी कोशिश की, लेकिन परीक्षार्थियों को उनके फैसले समझ में नहीं आए और उन्होंने परीक्षा में फेल हो गए। उसे अपने दम पर सीखना था। न तो गॉस और न ही पॉइसन, जिनके पास उन्होंने अपने काम भेजे थे, उन्हें भी समझा, लेकिन उनका सिद्धांत बीसवीं सदी के 60 के दशक में बहुत उपयोगी था, और हमारे समय में सक्रिय रूप से गणित की नई शाखाओं में सैद्धांतिक गणना के लिए दोनों का उपयोग किया जाता है, और अभ्यास करते हैं।

हम उनके समूह सिद्धांत से निम्नलिखित सरल निष्कर्षों का उपयोग करेंगे। मुख्य विचार - एक परिमित (और अनंत नहीं) संख्या है, जिसे एक क्षेत्र कहा जाता है, जिसके साथ आप सभी गणितीय कार्यों को अंजाम दे सकते हैं। क्षेत्र में संख्याओं की संख्या किसी भी प्राकृतिक डिग्री में एक प्रमुख संख्या होनी चाहिए, हालांकि, यहां चर्चा की गई सरल रीड-सोलोमन कोड के मामले में, क्षेत्र का आयाम 1 डिग्री में एक प्रमुख संख्या है। विस्तारित रीड-सोलोमन कोड में, डिग्री 1 से अधिक है।
उदाहरण के लिए, आयाम 7 के गैलोज़ क्षेत्र के लिए, अर्थात्। GF (7), सभी गणितीय कार्य 0,1,2,3,4,5,6 संख्याओं के साथ होंगे।
उदाहरण जोड़: 1 + 2 = 3; 4 + 5 = 9 मॉड 7 = 2। गैलोजेन क्षेत्रों में परिवर्धन मोडुलो जोड़ है। घटाव और गुणा भी मोडुलो किया जाता है।
विभाजन का उदाहरण: 5/6 = 30/36 = 30 / (36 मॉड 7) = 30/1 = 30 = 30 मॉड 7 = 2।
एक डिग्री का निर्माण गुणन के समान है।

एक उपयोगी संपत्ति गैलोज़ियन क्षेत्रों में घातांक के दौरान पाई जाती है। जैसा कि आप देख सकते हैं, यदि आप चयनित गैलोज़ फील्ड GF (7) में 3 या 5 की शक्ति बढ़ाते हैं, तो लाइन में वर्तमान गैलोजेन फ़ील्ड के सभी तत्व शामिल हैं सिवाय 0. ऐसी संख्याओं को आदिम तत्व कहा जाता है। रीड-सोलोमन कोड आम तौर पर चयनित गलाइस फ़ील्ड के सबसे बड़े आदिम तत्व का उपयोग करते हैं। GF (7) के लिए, यह 5 है।
यह ध्यान दिया जा सकता है कि गैलोज क्षेत्रों में संख्याएँ एक ही समय में, अमूर्तताएं हैं जो सामान्य संख्याओं की तुलना में एक दूसरे से अधिक निकटता से संबंधित हैं।

प्रक्षेप

जैसा कि कई लोग जानते हैं कि स्कूल वर्ष के बाद से, प्रक्षेप किसी दिए गए सेट में न्यूनतम डिग्री के बहुपद की खोज है। उदाहरण के लिए, इन बिंदुओं पर कुछ फ़ंक्शन के तीन बिंदु और तीन मान हैं। आप एक फ़ंक्शन पा सकते हैं जो इस इनपुट को संतुष्ट करता है। उदाहरण के लिए, लैगरेंज परिवर्तन का उपयोग करना बहुत सरल है। फ़ंक्शन पाए जाने के बाद, आप कई और बिंदु बना सकते हैं, और ये बिंदु तीन शुरुआती बिंदुओं से जुड़े होंगे। एन्कोडिंग के दौरान अनावश्यक वर्ण उत्पन्न करना प्रक्षेप के समान एक ऑपरेशन है।

उलटा असतत फूरियर रूपांतरण (IDFT)

गल्र्स समूहों के सिद्धांत के साथ फूरियर रूपांतरण गणितीय विचार का एक और शिखर है, जिसका उपयोग वर्तमान में कई क्षेत्रों में किया जाता है। कुछ का यह भी मानना ​​है कि फूरियर रूपांतरण ब्रह्मांड के मौलिक कानूनों में से एक का वर्णन करता है। मुख्य बिंदु: परिमित लंबाई के किसी भी गैर-आवधिक संकेत को विभिन्न आवृत्तियों और चरणों के साइनसोइड्स के योग के रूप में दर्शाया जा सकता है, फिर आप उनसे मूल संकेत को फिर से संगठित कर सकते हैं। हालाँकि, यह केवल वर्णन नहीं है। गलाइस क्षेत्रों में संख्याएँ साइनसोइड्स की अलग-अलग आवृत्तियों से मिलती-जुलती हैं, इसलिए फूरियर ट्रांसफॉर्म का उपयोग उनके लिए भी किया जा सकता है।
असतत फूरियर रूपांतरण असतत मूल्यों के लिए फूरियर रूपांतरण सूत्र है। रूपांतरण की दो दिशाएँ हैं - प्रत्यक्ष और रिवर्स। व्युत्क्रम रूपांतर गणितीय रूप से सरल है, इसलिए आइए इस शब्द को विचार C = (3,1,0,0,0,0) के साथ कोडित करें। पहले दो अक्षर सूचना हैं, अंतिम चार निरर्थक हैं और हमेशा 0 हैं।
हम एक बहुपद के रूप में कोडवर्ड C लिखते हैं: C = 3 * x ⁰ + 1 * x ¹ + 0 * x ² + ... = 3 + x। गैलोज़ के क्षेत्र के रूप में, हम उपरोक्त GF (7) को लेते हैं, जहां आदिम तत्व = 5. आईडीएफटी करके, हम विभिन्न डिग्री के आदिम तत्व z के लिए बहुपद C ​​के मानों को पाते हैं। IDFT सूत्र: c _j = C (z ^j )। यही है, हम फ़ंक्शन सी (जेड ^जे ) के मूल्यों को खोजते हैं, जहां जे गैलोइस फील्ड जीएफ (7) के तत्व हैं। हम j = N-2 = 7-2 = 5 डिग्री तक गिनते हैं। डिग्री तालिका को देखते हुए, कोई अनुमान लगा सकता है कि क्यों: छठे डिग्री तक, मान फिर से 1 है, अर्थात्। दोहराता है, जिसके परिणामस्वरूप यह निर्धारित करना असंभव होगा कि वे किस डिग्री में उठाए गए थे - 6 वीं या 0 वीं में।
c ₀ = C (z ⁰ ) = 3 + 1 * z ⁰ = 3 + 1 * 5 ⁰ = 4
c ₁ = C (z ¹ ) = 3 + 1 * z ¹ = 8 = 1
c ₂ = C (z ² ) = 3 + 1 * z ² = 0
...
इस प्रकार, C (3,1,0,0,0,0) => s (4,1,0,2,5,6)।

हम शब्द c (4,1,0,2,5,6) पास करते हैं।

त्रुटि

एक त्रुटि एक और शब्द है जो प्रेषित के साथ है। उदाहरण के लिए, त्रुटि f = (0,0,0,2,0,6)। यदि + f के साथ किया जाता है, तो हम _f (4,1,0,4,5,5) के साथ प्राप्त करते हैं।

डायरेक्ट फूरियर ट्रांसफॉर्म (DFT)। डिकोडिंग। सिंड्रोम

रिसीवर पर, हमें c + f = c _f (4,1,0,4,5,5) शब्द मिला। ट्रांसमिशन त्रुटियों की जांच कैसे करें? यह ज्ञात है कि हमने GF (7) में IDFT का उपयोग करके जानकारी एन्कोड की थी। DFT (असतत फूरियर ट्रांसफॉर्म) IDFT का विलोम है। ऐसा करने के बाद, आप प्रारंभिक जानकारी और चार शून्य (यानी, C (3,1,0,0,0,0)) प्राप्त कर सकते हैं, अगर कोई त्रुटि नहीं थी। यदि त्रुटियां थीं, तो इन चार शून्य के बजाय अन्य अंक होंगे। चलो एफ के साथ डीएफटी करें और जांच करें कि क्या कोई त्रुटि है। DFT सूत्र: C _k = N ^-1 * c (z ^-kj )। फ़ील्ड GF (7) का आदिम तत्व z = 5 अभी भी उपयोग किया जाता है।
C ₀ = c (5 ^{-0 * j} ) / 6 = (4 * 5 ^{-0 * 0} + 1 * 5 ^{-1 * 0} + 0 * 5 ^{-2 * 0} + 4 * 5 ^{-3 * 0} + 5 * 5 ^{-4 * 0} + 5 * 5 ^{-5 * 0} ) / 6 = (4 + 1 + 4 + 0 + 5 + 5) / 6 = 19/6 = 5/6 = 30/36 = 30 = 2;
C ₁ = c (5 ^{-1 * j} ) / 6 = (4 * 5 ^{-0 * 1} + 1 * 5 ^{-1 * 1} + 0 * 5 ^{-2 * 1} + 4 * 5 ^{-3 * 1} + 5 * 5 ^{-4 * 1} + 5 * 5 ^{-5 * 1} ) / 6 = (4 + 3/15 + 24/750 + 20/2500 + 25/15625) / 6 = (4 + 3 + 24 + 20 + 25) / 6 = 76/6 = 456/36 = 456 = 1;
सी ₂ = सी (5 ^{-2 * जे} ) / 6 = (4 * 5 ^{-0 * 2} + 1 * 5 ^{-1 * 2} + 0 * 5 ^{-2 * 2} + 4 * 5 ^{-3 * 2} + 5 * 5 ^{-4 * 2} + 5 * 5 ^{-5 * 2} ) / 6 = (4 + 2 + 4 + 10 + 20) / 6 = 40/6 = 240/36 = 240 = 2;
...
_f (4,1,0,4,5,5) के साथ => C _f ( 2,1,2,1,0,5 )। यदि कोई त्रुटि नहीं थी, तो हाइलाइट किए गए वर्ण शून्य होंगे। अब आप देख सकते हैं कि त्रुटि थी। इस मामले में, प्रतीकों 2,1,0,5 को त्रुटि सिंड्रोम कहा जाता है।

त्रुटि स्थिति की गणना के लिए बर्लेकैंप-मेस्सी एल्गोरिदम

त्रुटि को ठीक करने के लिए, आपको यह जानना होगा कि कौन से अक्षर त्रुटि से प्रेषित किए गए थे। इस स्तर पर, यह गणना की जाती है कि गलत चरित्र कहां हैं, कितनी त्रुटियां थीं, और यह भी कि क्या ऐसी त्रुटियों को ठीक करना संभव है।
बर्लेकैंप-मेस्सी एल्गोरिथ्म एक बहुपद के लिए खोज करता है, जब सिंड्रोम की संख्या से तैयार एक विशेष मैट्रिक्स द्वारा गुणा किया जाता है (उदाहरण के लिए नीचे), एक शून्य वेक्टर लौटाएगा। एल्गोरिथ्म के प्रमाण से पता चलता है कि इस बहुपद की जड़ों में परिणामी कोडवर्ड में त्रुटियों के साथ पात्रों की स्थिति के बारे में जानकारी है।
चूंकि विचाराधीन मामले के लिए त्रुटियों की अधिकतम संख्या 2 हो सकती है, इसलिए हम दो त्रुटियों के लिए मैट्रिक्स के रूप में वांछित बहुपद का सूत्र लिखते हैं (डिग्री 2 का बहुपद): खेल = [1 मोटोरोला 1]।
अब हम Toeplitz मैट्रिक्स के प्रारूप में सिंड्रोम (2,1,0,5) लिखते हैं। यदि आप सिंड्रोम और परिणामी मैट्रिक्स को देखते हैं, तो आप तुरंत इस तरह के मैट्रिक्स को बनाने के सिद्धांत को नोटिस करेंगे। मैट्रिक्स का आयाम बहुपद is के कारण है जो ऊपर इंगित किया गया है।

हल किया जाने वाला समीकरण:

प्रश्न चिह्न के तहत परिणाम परिणाम को प्रभावित नहीं करते हैं। जी 1 और जी 2 को खोजने के लिए आवश्यक है, वे त्रुटियों की स्थिति के लिए जिम्मेदार हैं। हम धीरे-धीरे उस आयाम को बढ़ाएंगे जिसके साथ हम काम करते हैं। हम 1x1 के न्यूनतम आयाम के साथ 1 और मैट्रिक्स के निचले बाएं किनारे से शुरू करते हैं (हरे रंग में चिह्नित)।

आयाम बढ़ाएं। मान लीजिए हमें G1 की स्थिति में कोई त्रुटि नहीं है। फिर Then1 = 0।

गणना के आयाम को बढ़ाने के लिए हमें दाईं ओर [0 0] या पहले से कम से कम एक 0 प्राप्त करना चाहिए, लेकिन पहली जगह में यह 1. हम G1 के लिए एक मान चुन सकते हैं (जो अभी 0 है) ताकि हमें दाईं ओर आवश्यक 0 प्राप्त हो। एल्गोरिथ्म में G1 के मूल्य का चयन करने की प्रक्रिया अनुकूलित है। हम आपके द्वारा एक और बार विचार किए गए दो समीकरणों को लिखते हैं, और तीसरे समीकरण को भी प्राप्त करते हैं, जो G1 की गणना करता है। कलर्स शो जहां जाता है।

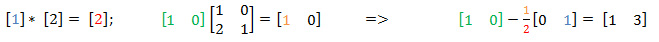
यानी G1 = 3. मैं आपको याद दिलाता हूं कि गिनती GF (7) के पास जाती है। यह भी ध्यान देने योग्य है कि G1 मान अस्थायी है। जी 2 गणना के दौरान, यह बदल सकता है। हम दाईं ओर फिर से पढ़ते हैं:

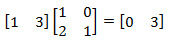
दाईं ओर 0 मिला, अब आयाम बढ़ाएं। हम मानते हैं, सादृश्य द्वारा, कि G2 = 0. हम पाया G1 = 3 का उपयोग करते हैं।

सबसे पहले, दाईं ओर के तीनों के बजाय, आपको पिछले वाले 0. एक्ट्स के अनुरूप होने की आवश्यकता है। अगला, जी 2 के मूल्य का चयन।

हम मुख्य समीकरण में नया मान 2 = 2 लिखते हैं और फिर से दाईं ओर मान ढूँढने की कोशिश करते हैं:

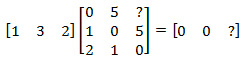
इस चरण में कार्य केवल पहला शून्य प्राप्त करना था, हालांकि, संयोग से, मैट्रिक्स का दूसरा तत्व भी शून्य हो गया, अर्थात। समस्या हल हो गई है। यदि यह शून्य नहीं था, तो हम एक बार फिर से मूल्यों का चयन करेंगे (इस बार G1 और G2 दोनों के लिए), चयन का आयाम बढ़ाते हुए। यदि आप इस एल्गोरिथ्म में रुचि रखते हैं, तो यहां दो और उदाहरण हैं।
तो, जी 1 = 3, जी 2 = 2. जी 1 और जी 2 के लिए नॉनजरो मान बताते हैं कि 2 त्रुटियां थीं। हम मैट्रिक्स को एक बहुपद के रूप में लिखते हैं: z (z) = 1 + 3x + 2x ² । जड़ों, आदिम तत्व की डिग्री को ध्यान में रखते हुए, जिसमें परिणाम 0 है:
जी (5 ³ ) = 1 + 3 * 6 + 2 * 6 ² = 91 = 13 * 7 = 0।
जी (5 ⁵ ) = 1 + 3 * 3 + 2 * 3 ² = 28 = 0।
इसका अर्थ है 3 और 5 की स्थिति में त्रुटियां।
इसी प्रकार, आप यह सुनिश्चित करने के लिए शेष मान पा सकते हैं कि वे शून्य नहीं देते हैं:
जी => जी (जेड ^जे ) = (3,5,5,0,4,0)। जैसा कि आपने देखा होगा, IDFT का उपयोग फिर से GF (7) में किया जाता है।

Forni त्रुटि सुधार

पिछले चरण में, त्रुटि पदों की गणना की गई थी, अब यह सही मानों को खोजने के लिए बनी हुई है। एक बहुपद का वर्णन करने वाले त्रुटि स्थान: G (z) = 1 + 3x + 2x ² । हम इसे सामान्यीकृत रूप में लिखते हैं, 4 से गुणा करते हैं और GF (7) के गुणों का उपयोग करते हैं: खेल (z) = x ² + 5x + 4।
फ़ॉर्नी की विधि लैग्रेग प्रक्षेप पर आधारित है और हम बहेलकैंप-मेसो एल्गोरिथ्म में संचालित बहुपद का उपयोग करते हैं।
विधि अतिरिक्त रूप से उन वर्णों की गणना करती है जो उन स्थानों पर खड़े होते हैं जो सिंड्रोम से संबंधित नहीं हैं। ये ऐसे पद हैं जो वास्तविक मूल्यों के अनुरूप हैं, हालांकि, अन्य मूल्यों की गणना उनके लिए की जाती है, जो त्रुटि सिंड्रोम और बहुपद जी के दृढ़ संकल्प से प्राप्त होते हैं। ये सिंड्रोम के साथ मिलकर नए मानों की गणना करते हैं जो त्रुटि मास्क बनाते हैं। अगला, IDFT किया जाता है और परिणाम एक प्रत्यक्ष त्रुटि है जो पहले प्रसारित कोडवर्ड के साथ अभिव्यक्त किया गया था। यह प्राप्त शब्द से घटाया जाता है और हमें मूल शब्द प्रेषित होता है। फिर हम प्रेषित कोडवर्ड के लिए डीएफटी करते हैं और अंत में जानकारी प्राप्त करते हैं। अगला, इस उदाहरण के संदर्भ में यह कैसे होता है।

हम त्रुटि सदिश F लिखते हैं (अंतिम 4 वर्ण वे सिंड्रोम हैं जिनका हम लगातार उपयोग करते हैं, दो प्रश्न चिह्न सूचना वर्णों के स्थानों पर हैं, यह त्रुटि मुखौटा है) और हम प्रत्येक वर्ण को अक्षर के साथ नामित करेंगे:

त्रुटि लोकेटर बहुपद मोटोरोला (z) = x2 + 5x + 4 के प्रतीकों को निम्नानुसार दर्शाया गया है:
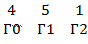
पिछले अनुभाग में टोप्लेट्ज़ मैट्रिक्स द्वारा बहुपद the का गुणा, वास्तव में, एक चक्रीय संकल्प ऑपरेशन था: यदि आप रैखिक समीकरण लिखते हैं जो मैट्रिक्स से प्राप्त होते हैं, तो आप देख सकते हैं कि सिंड्रोम (टोप्लेट्ज़ मैट्रिक्स के मूल्यों) से लिया गया मान बस समीकरण से समीकरण में बदल जाता है। स्थानों में, एक निश्चित दिशा में क्रमिक रूप से आगे बढ़ना, और इसे एक दृढ़ संकल्प कहा जाता है। मैंने जानबूझकर इस पैराग्राफ की शुरुआत में एक-दूसरे के ऊपर बहुपद एफ और जी रखा, ताकि आप नेत्रहीन रूप से बहुपद को आगे बढ़ाते हुए संकल्प (एक निश्चित क्रम में गुणा कर) कर सकें। पिछले खंड से मैट्रिक्स समीकरण का विस्तार करना और बहुपत्नी एफ और introduced के लिए संकेतन का उपयोग करके केवल प्रस्तुत किया गया है:
0 * F4 + 1 * F3 + 2 * F2 = 0
0 * F5 + 1 * F4 + 2 * F3 = 0
इससे पहले, संलक्षण केवल सिंड्रोम के लिए किया जाता था, फ़ॉर्नी विधि में, आपको F0 और F1 के लिए दृढ़ संकल्प की आवश्यकता होती है, और फिर उनके मान पाते हैं:
0 * F3 + 1 * F2 + 2 * F1 = 0
0 * F2 + 1 * F1 + 2 * F0 = 0
F0 = -G0 * F3 - G1 * F2 = 0
F1 = -G0 * F2 - G1 * F1 = 6
यही है, एफ = (6,0,2,1,0,5)। हम आईडीएफटी को अंजाम देते हैं, क्योंकि त्रुटि उस शब्द के साथ सम्‍मिलित थी जो आईडीएफटी एनकोडेड फॉर्म में था: f = (0,0,0,2,0,6)।
परिणामी कोडवर्ड cf से त्रुटि f को घटाएं: (4,1,0,4,5,5) - (0,0,0,2,0,6) = s (4,1,0,2,5,6) )
हम इस शब्द के लिए एक DFT बनाते हैं: c (4,1,0,2,5,6) => C = (3,1,0,0,0,0)। और यहाँ हमारे चरित्र 3 और 1 हैं, जिन्हें प्रसारित करने की आवश्यकता है।

निष्कर्ष

आमतौर पर, विस्तारित रीड-सोलोमन कोड का उपयोग किया जाता है, अर्थात, गैलोज़ फ़ील्ड दो (जीएफ (2 ^मीटर )) की शक्ति है, उदाहरण के लिए, सूचना बाइट्स को एन्कोडिंग। कार्य एल्गोरिदम उनके समान हैं जो इस लेख में चर्चा किए गए हैं।
एल्गोरिथ्म की कई किस्में हैं जो आवेदन के क्षेत्रों के साथ-साथ प्रत्येक विशेष किस्म की उम्र और विकास कंपनी पर निर्भर करती हैं। एल्गोरिथ्म जितना छोटा होगा, यह उतना ही जटिल होगा।

साथ ही, कई डिवाइस पूर्वनिर्धारित त्रुटि तालिकाओं का उपयोग करते हैं। गैलोज अंकगणित का उपयोग करते समय, संभावित त्रुटियों की एक सीमित संख्या प्राप्त की जाती है। इस संपत्ति का उपयोग गणना की संख्या को कम करने के लिए किया जाता है। यहां, यदि सिंड्रोम गैर-शून्य हो जाता है, तो इसकी तुलना संभवतया गलत सिंड्रोम वाले टेबल के साथ की जाती है।

कई लोगों के लिए, कोडिंग सिद्धांत में एक कोर्स अक्सर सबसे कठिन में से एक होता है। मुझे खुशी होगी अगर यह लेख किसी को इस विषय को तेजी से समझने में मदद करता है।