एक सामान्य वितरण के साथ सब कुछ सामान्य क्यों है?

सामान्य वितरण (गॉसियन डिस्ट्रीब्यूशन) ने प्रायिकता सिद्धांत में एक केंद्रीय भूमिका निभाई है, क्योंकि यह कई कारकों के प्रभाव के परिणामस्वरूप बहुत बार उत्पन्न होता है, जिनमें से किसी एक का योगदान नगण्य है। केंद्रीय सीमा प्रमेय (CLT) वस्तुतः सभी अनुप्रयुक्त विज्ञानों में अनुप्रयोग पाता है, जिससे सांख्यिकी तंत्र सार्वभौमिक बन जाता है। हालाँकि, बहुत बार ऐसे मामले आते हैं जब इसका अनुप्रयोग असंभव होता है, और शोधकर्ता हर संभव तरीके से कोशिश कर रहे हैं कि परिणामों का समायोजन एक गाऊसी के लिए किया जाए। यहां कई कारकों के वितरण पर प्रभाव के मामले में एक वैकल्पिक दृष्टिकोण है, अब मैं बताऊंगा।

केंद्रीय हीटिंग सिस्टम का एक संक्षिप्त इतिहास। जीवित न्यूटन के साथ भी, अब्राहम डी मोइरे स्वतंत्र वितरण की एक श्रृंखला में एक घटना की टिप्पणियों के केंद्रीकृत और सामान्यीकृत संख्या के अभिसरण पर एक प्रमेय साबित हुए। 19 वीं और 20 वीं शताब्दी की शुरुआत में, इस प्रमेय ने सामान्यीकरण के लिए एक वैज्ञानिक मॉडल के रूप में कार्य किया। लाप्लास ने समान वितरण के मामले को साबित किया, पोइसन ने विभिन्न संभावनाओं के साथ मामले के लिए स्थानीय प्रमेय साबित किया। पॉइनकेयर, लीजेंड्रे एंड गॉस ने सामान्य वितरण के लिए त्रुटियों के अभिसरण के आधार पर अवलोकन त्रुटियों और कम से कम वर्गों की विधि का एक समृद्ध सिद्धांत विकसित किया। अभियान में क्षणों की विधि को विकसित करके यादृच्छिक चर के योग के लिए चेबीशेव ने और भी मजबूत प्रमेय साबित किया। 1900 में लीपुनोव, चेबीशेव और मार्कोव पर भरोसा करते हुए, टीएसपी को अपने वर्तमान रूप में साबित किया, लेकिन केवल तीसरे क्रम के क्षणों के अस्तित्व के साथ। और केवल 1 9 34 में, फेलर ने एक अंत डाल दिया, यह दिखाते हुए कि दूसरे क्रम के क्षणों का अस्तित्व एक आवश्यक और पर्याप्त स्थिति दोनों है।

सीएलटी को निम्नानुसार तैयार किया जा सकता है: यदि यादृच्छिक चर स्वतंत्र, समान रूप से वितरित होते हैं और शून्य के अलावा एक परिमित विचरण करते हैं, तो इन मात्राओं के केंद्र (सामान्यीकृत) सामान्य नियम में परिवर्तित हो जाते हैं। यह इस रूप में है कि यह प्रमेय विश्वविद्यालयों में पढ़ाया जाता है और यह अक्सर पर्यवेक्षकों और शोधकर्ताओं द्वारा उपयोग किया जाता है जो गणित में पेशेवर नहीं हैं। उसका क्या कसूर है? वास्तव में, प्रमेय को उन क्षेत्रों में पूरी तरह से लागू किया जाता है जो गॉस, पोंकारे, चेबीशेव और 19 वीं शताब्दी के अन्य जीनियस ने काम किया, अर्थात्: अवलोकन त्रुटियों, सांख्यिकीय भौतिकी, कम से कम वर्ग, जनसांख्यिकीय अध्ययन और शायद कुछ और का सिद्धांत। लेकिन जिन वैज्ञानिकों के पास खोजों के लिए मौलिकता की कमी है वे सामान्यीकरण में लगे हुए हैं और इस प्रमेय को हर चीज पर लागू करना चाहते हैं, या सामान्य वितरण को अपने कानों से खींचना चाहते हैं, जहां यह बस मौजूद नहीं हो सकता है। आपको उदाहरण चाहिए, मेरे पास हैं।

बुद्धि गुणांक। प्रारंभ में, इसका अर्थ है कि लोगों की बुद्धिमत्ता सामान्य रूप से वितरित की जाती है। वे एक ऐसा परीक्षण करते हैं जो इस तरह से पूर्व-संकलित होता है जो बकाया क्षमताओं को ध्यान में नहीं रखता है, लेकिन व्यक्तिगत रूप से समान कारकों को ध्यान में रखता है: तार्किक सोच, मानसिक डिजाइन, कम्प्यूटेशनल क्षमताएं, अमूर्त सोच और कुछ और। उन समस्याओं को हल करने की क्षमता, जो अधिकांश के लिए दुर्गम हैं, या परीक्षण को अल्ट्राफास्ट समय में पारित नहीं किया जाता है, और पहले परीक्षण पास करने से भविष्य में परिणाम (लेकिन बुद्धिमत्ता नहीं) बढ़ जाती है। और तब के राजनेताओं का मानना ​​है कि "कोई भी उनसे ज्यादा चालाक नहीं हो सकता है", "चलो दूर ले जाओ और समझदारों से विभाजित करें"।

दूसरा उदाहरण: वित्तीय संकेतकों में परिवर्तन। स्टॉक की कीमतों, मुद्रा उद्धरण, कमोडिटी विकल्पों में परिवर्तन के अध्ययन के लिए गणितीय आंकड़ों के उपयोग की आवश्यकता होती है, और यह विशेष रूप से महत्वपूर्ण है कि वितरण के प्रकार के साथ गलत नहीं किया जाए। बिंदु में एक मामला: 1997 में, अर्थशास्त्र में नोबेल पुरस्कार ब्लैक-स्कोल्स मॉडल के प्रस्ताव के लिए भुगतान किया गया था, इस धारणा के आधार पर कि स्टॉक संकेतक (तथाकथित सफेद शोर) में वृद्धि का वितरण सामान्य है। उसी समय, लेखकों ने स्पष्ट रूप से कहा कि इस मॉडल को स्पष्ट करने की आवश्यकता है, लेकिन उन सभी को जो आगे के शोधकर्ताओं ने करने का फैसला किया, वह बस पॉइसन वितरण को सामान्य वितरण में जोड़ना था। यहां, जाहिर है, लंबे समय की श्रृंखला के अध्ययन में गलतियां होंगी, चूंकि पॉइसन वितरण सीएलटी को बहुत अच्छी तरह से संतुष्ट करता है, और यहां तक ​​कि 20 शर्तों के साथ यह सामान्य वितरण से अप्रभेद्य है। नीचे दी गई तस्वीर को देखो (और यह एक बहुत ही गंभीर आर्थिक पत्रिका से है), यह दर्शाता है कि, काफी बड़ी संख्या में टिप्पणियों और स्पष्ट विकृतियों के बावजूद, एक धारणा बनाई गई है कि वितरण सामान्य है।



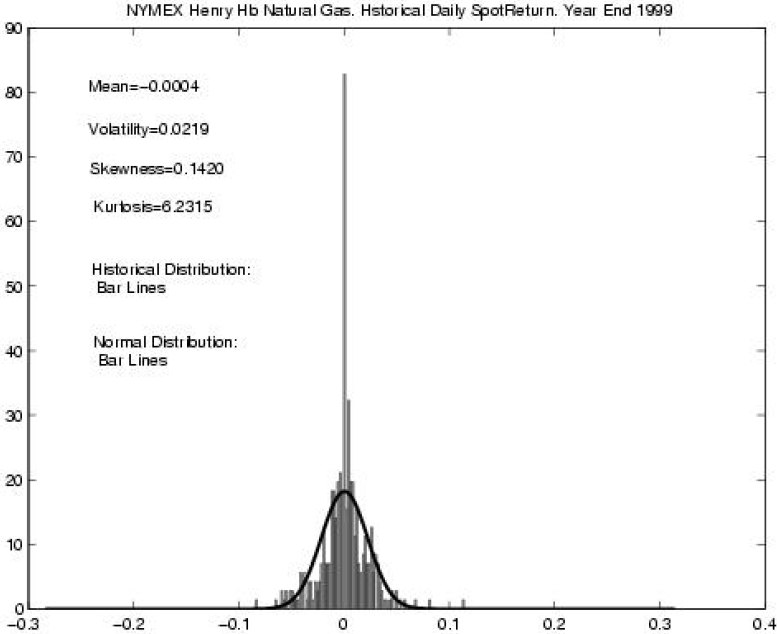
यह बहुत स्पष्ट है कि शहर की आबादी के बीच मजदूरी का वितरण, डिस्क पर फ़ाइल आकार और शहरों और देशों की आबादी सामान्य नहीं होगी।

इन उदाहरणों से वितरण की सामान्य विशेषता तथाकथित "भारी पूंछ" की उपस्थिति है, अर्थात, औसत से बहुत दूर के मूल्य, और ध्यान देने योग्य विषमता, आमतौर पर सही है। आइए विचार करें कि सामान्य के अलावा और क्या, इस तरह के वितरण हो सकते हैं। हम पहले उल्लेख किए गए पॉइसन के साथ शुरू करते हैं: उसके पास एक पूंछ है, लेकिन हम चाहते हैं कि कानून को उन समूहों के समूह के लिए दोहराया जाए जिनमें से प्रत्येक में यह देखा गया है (उद्यम द्वारा फाइलों का आकार गिनें, कई शहरों के लिए वेतन) या बढ़ाया (मनमाने ढंग से या मॉडल अंतराल को कम करना) ब्लैक - स्कोल्स), जैसा कि अवलोकन दिखाते हैं, पूंछ और विषमता गायब नहीं होती है, लेकिन सीएलटी पर पॉइसन वितरण सामान्य हो जाना चाहिए। समान कारणों से, एरलांग वितरण, बीटा, लॉगऑनॉर्मल, और अन्य सभी विचरण के साथ काम नहीं करेंगे। यह केवल पारेटो वितरण में कटौती करने के लिए बनी हुई है, लेकिन यह न्यूनतम मूल्य के साथ मोड के संयोग के कारण उपयुक्त नहीं है, जो नमूना डेटा के विश्लेषण में लगभग नहीं पाया गया है।

आवश्यक गुणों वाले वितरण मौजूद हैं और स्थिर वितरण कहलाते हैं। उनका इतिहास भी बहुत दिलचस्प है, और 1935 में फेलर के काम के बाद एक प्रमुख प्रमेय साबित हुआ, फ्रांसीसी गणितज्ञ पॉल लेवी और सोवियत गणितज्ञ ए.वाय। Khinchin। सीएलटी को सामान्यीकृत किया गया था; फैलाव के अस्तित्व के लिए शर्त को इससे हटा दिया गया था। सामान्य के विपरीत, न तो घनत्व और न ही स्थिर यादृच्छिक चर का वितरण कार्य व्यक्त किया जाता है (दुर्लभ अपवादों के बारे में, जो नीचे चर्चा की जाएगी), उन सभी के बारे में जाना जाता है जो विशेषता फ़ंक्शन (वितरण घनत्व का उलटा फूरियर रूपांतरण है, लेकिन सार को समझना संभव नहीं है) जानने के लिए)।
तो, प्रमेय: यदि यादृच्छिक चर स्वतंत्र होते हैं, समान रूप से वितरित किए जाते हैं, तो इन राशियों के योग एक स्थिर कानून में परिवर्तित हो जाते हैं।

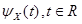
अब परिभाषा है। रैंडम वैरिएबल X स्थिर होगा और यदि केवल इसकी विशेषता फ़ंक्शन का लघुगणक रूप में कल्पना करें:





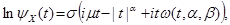
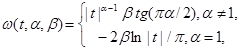
जहाँ ।

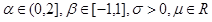
वास्तव में, यहां बहुत जटिल कुछ भी नहीं है, आपको बस चार मापदंडों का अर्थ समझाने की आवश्यकता है। मापदंडों सिग्मा और म्यू सामान्य पैमाने और ऑफसेट हैं, जैसा कि सामान्य वितरण में होता है, म्यू गणितीय अपेक्षा के बराबर होगा, अगर यह है, और यह तब है जब अल्फा एक से अधिक है। बीटा पैरामीटर विषमता है, जब यह शून्य के बराबर होता है, तो वितरण सममित होता है। लेकिन अल्फा एक विशेषता पैरामीटर है, यह इंगित करता है कि मात्रा के क्षण किस क्रम में मौजूद हैं, यह दो के करीब है, जितना अधिक वितरण सामान्य दिखता है, अगर दो समान हैं, तो वितरण सामान्य हो जाता है, और केवल इस मामले में बड़े आदेशों के क्षण भी होते हैं। सामान्य वितरण, विषमता पतित होती है। इस मामले में जब अल्फा एकता और बीटा शून्य है, कैची वितरण प्राप्त किया जाता है, और उस मामले में जहां अल्फा आधा है और बीटा लेवी वितरण है, अन्य मामलों में ऐसी मात्रा के वितरण घनत्व के लिए quadratures में कोई प्रतिनिधित्व नहीं है।
20 वीं शताब्दी में, स्थिर मात्रा और प्रक्रियाओं का एक समृद्ध सिद्धांत (जिसे लेवी प्रक्रियाओं कहा जाता है) विकसित किया गया था, उनके आंशिक अंशों के साथ संबंध दिखाया गया था, मानकीकरण और मॉडलिंग के विभिन्न तरीकों को पेश किया गया था, मापदंडों का कई तरीकों से मूल्यांकन किया गया था, और अनुमानों की स्थिरता और स्थिरता दिखाई गई थी। चित्र को देखें, इस पर 15 गुना बढ़े हुए टुकड़े के साथ लेवी प्रक्रिया का एक नकली प्रक्षेपवक्र है।



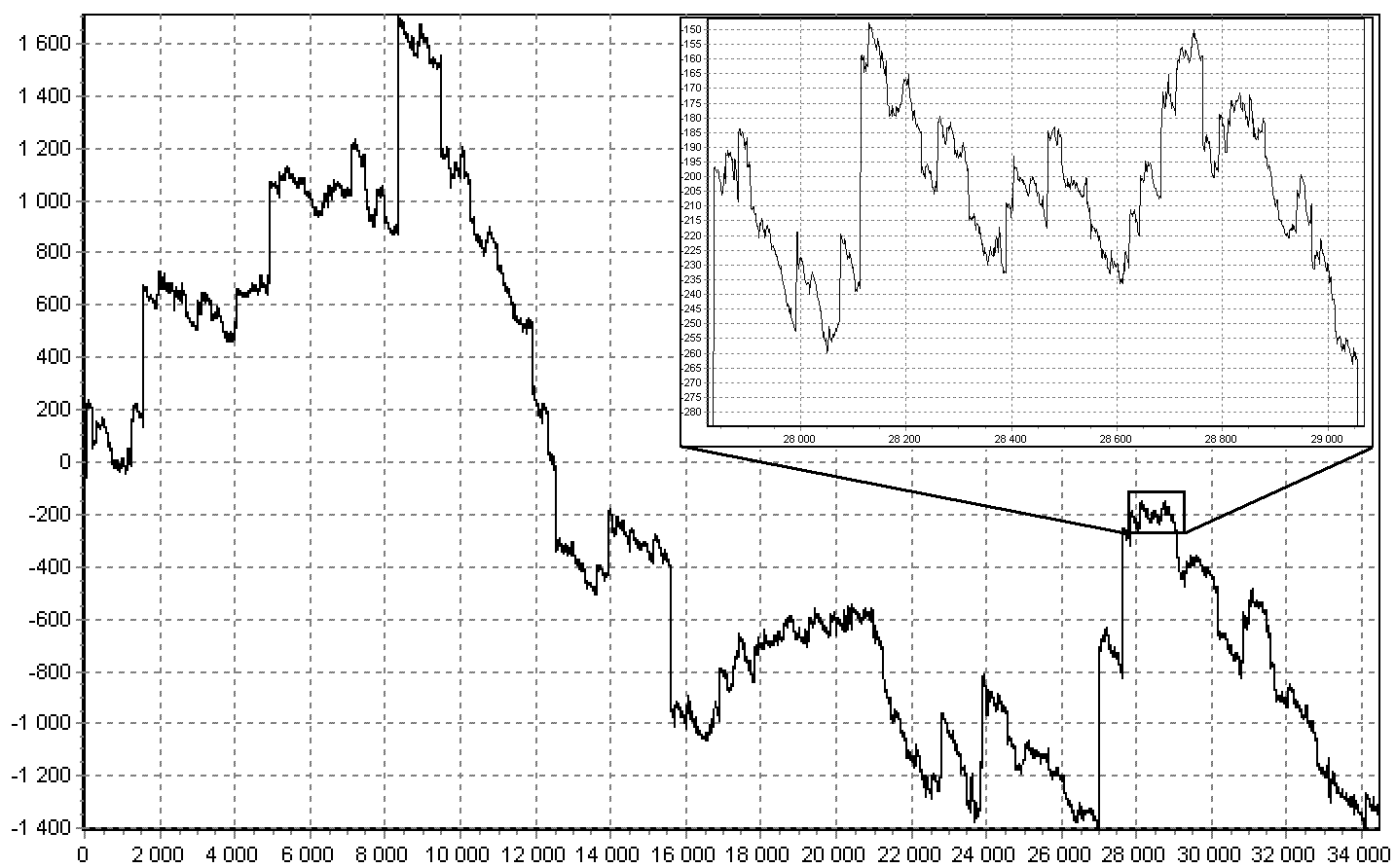
यह इस तरह की प्रक्रियाओं और वित्त में उनके आवेदन से निपटकर था कि बेनोइट मैंडलब्रॉट ने फ्रैक्टल्स का आविष्कार किया था। हालांकि, हर जगह इतना अच्छा नहीं था। 20 वीं शताब्दी के उत्तरार्ध में लागू और साइबरनेटिक विज्ञान की सामान्य प्रवृत्ति के तहत पारित हुआ, और इसका मतलब शुद्ध गणित का संकट था, हर कोई उत्पादन करना चाहता था, लेकिन सोचना नहीं चाहता था, उनकी पत्रकारिता के साथ मानविकी ने गणितीय क्षेत्र पर कब्जा कर लिया। उदाहरण: अमेरिकन मोस्टलेर, समस्या नंबर 11 द्वारा पुस्तक "समाधानों के साथ संभावित मनोरंजक संभाव्य समस्याएं"।



लेखक की इस समस्या का हल केवल सामान्य ज्ञान की हार है:


यही स्थिति 25 वीं समस्या के साथ है, जहां तीन विरोधाभासी उत्तर दिए गए हैं।

लेकिन वापस स्थायी वितरण के लिए। इस लेख के बाकी हिस्सों में, मैं यह दिखाने की कोशिश करूंगा कि उनके साथ काम करते समय कोई अतिरिक्त कठिनाई नहीं होनी चाहिए। अर्थात्, ऐसे संख्यात्मक और सांख्यिकीय तरीके हैं जो किसी को मापदंडों का अनुमान लगाने, वितरण फ़ंक्शन की गणना करने और उन्हें मॉडल करने की अनुमति देते हैं, अर्थात, किसी अन्य वितरण के साथ उसी तरह काम करते हैं।

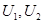
स्थिर यादृच्छिक चर मॉडलिंग। चूंकि सब कुछ तुलना में जाना जाता है, मैं सबसे पहले सबसे सुविधाजनक याद करूंगा, गणना के दृष्टिकोण से, एक सामान्य मूल्य (बॉक्स-मुलर विधि) उत्पन्न करने की विधि: यदि मूल यादृच्छिक चर (समान रूप से [0, 1) और स्वतंत्र पर वितरित किए जाते हैं, फिर संबंध द्वारा

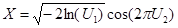
मानक सामान्य मूल्य प्राप्त किया जाता है।

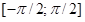
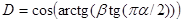
अब हमें अल्फा और बीटा को पूर्वनिर्धारित करते हैं, V और W को स्वतंत्र यादृच्छिक चर बनाते हैं: V को समान रूप से वितरित किया जाता है , डब्ल्यू घातांक 1 पैरामीटर के साथ वितरित किया जाता है, हम परिभाषित करते हैं और , फिर अनुपात द्वारा:

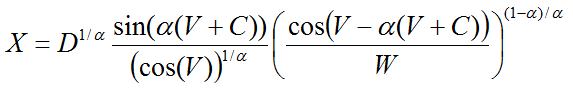
हम एक स्थिर यादृच्छिक चर प्राप्त करते हैं जिसके लिए म्यू शून्य है और सिग्मा एकता है। यह तथाकथित मानक स्थिर मूल्य है, जो सामान्य मामले (अल्फा के साथ एकता के बराबर नहीं) के लिए, यह पैमाने से गुणा करने और ऑफसेट को जोड़ने के लिए पर्याप्त है। हां, अनुपात अधिक जटिल है, लेकिन स्प्रेडशीट ( लिंक ) में भी इसका उपयोग करना काफी सरल है। नीचे दिए गए आंकड़े ब्लैक - स्कोल्स मॉडल के मॉडलिंग प्रक्षेपवक्र दिखाते हैं, पहले एक सामान्य और फिर एक स्थिर प्रक्रिया के लिए।






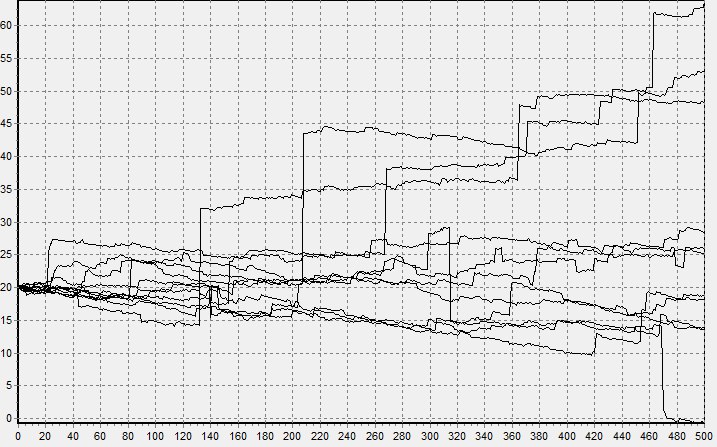
आप विश्वास कर सकते हैं कि एक्सचेंजों पर मूल्य परिवर्तन की अनुसूची दूसरे की तरह अधिक है।

स्थायी वितरण मापदंडों का अनुमान। चूँकि Habré पर सूत्र सम्मिलित करना काफी कठिन है, मैं सिर्फ एक लेख के लिए एक लिंक छोड़ता हूँ जहाँ मापदंडों के मूल्यांकन के लिए सभी तरह के विभिन्न तरीकों पर विस्तार से चर्चा की जाती है, या रूसी में मेरे लेख पर, जहाँ केवल दो विधियाँ दी गई हैं। आप एक अद्भुत पुस्तक भी देख सकते हैं जो स्थिर यादृच्छिक चर और उनके अनुप्रयोगों के पूरे सिद्धांत (ज़ोलोटेरेव वी।, उचैकिं वी। स्थिर वितरण और उनके अनुप्रयोग। वीएसपी एम। एम। 1999:), या पूरी तरह से वैज्ञानिक रूसी संस्करण (ज़ोलोटेरेव वी) को संकलित करती है। .M। स्थिर एक-आयामी वितरण। - एम .: विज्ञान, भौतिकी और गणित के मुख्य संस्करण, 1983 - 304 पी।)। घनत्व और वितरण समारोह की गणना करने के तरीके भी इन पुस्तकों में मौजूद हैं।

निष्कर्ष के रूप में, मैं केवल सिफारिश कर सकता हूं, जब सांख्यिकीय डेटा का विश्लेषण करते समय, जब एक विषमता या मूल्य होते हैं जो अपेक्षा से बहुत अधिक होते हैं, तो खुद से पूछें: "वितरण कानून सही है?" और "सामान्य वितरण के साथ सब कुछ सामान्य है?"