💂 🧢 👩‍🔧 एल्गोरिथम जटिलता विश्लेषण का परिचय (भाग 3) 👨‍💻 🏴‍☠️ 👩🏽

अनुवादक से: यह पाठ मामूली "संक्षिप्त रूप से" चबाने वाली सामग्री के स्थानों के कारण दिया गया है। लेखक सही चेतावनी देता है कि कुछ विषय पाठक को बहुत सरल या प्रसिद्ध लग सकते हैं। फिर भी, मेरे लिए व्यक्तिगत रूप से इस पाठ ने एल्गोरिदम की जटिलता के विश्लेषण पर मौजूदा ज्ञान को कारगर बनाने में मदद की। मुझे उम्मीद है कि यह किसी और के लिए उपयोगी होगा।
मूल लेख की बड़ी मात्रा के कारण, मैंने इसे भागों में तोड़ दिया, जिसमें से कुल चार होंगे।
मैं (हमेशा की तरह) अनुवाद की गुणवत्ता में सुधार पर पीएम की किसी भी टिप्पणी के लिए बहुत आभारी रहूंगा।

पहले प्रकाशित:
भाग 1
भाग २

लघुगणक

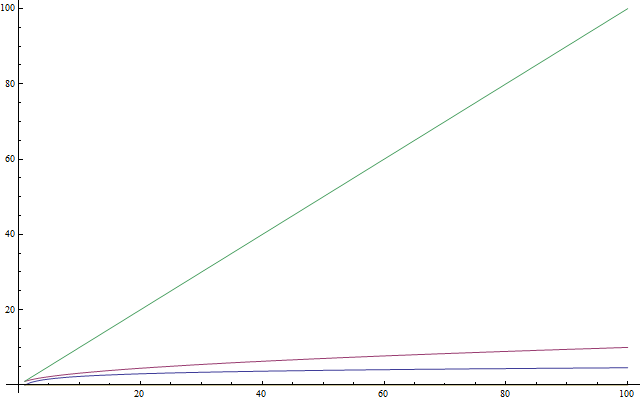
यदि आप जानते हैं कि लघुगणक क्या हैं, तो आप सुरक्षित रूप से इस अनुभाग को छोड़ सकते हैं। अध्याय उन लोगों के लिए है जो इस अवधारणा से अपरिचित हैं या इसका उपयोग शायद ही कभी करते हैं कि वे पहले ही भूल चुके हैं कि क्या है। लघुगणक महत्वपूर्ण हैं क्योंकि वे जटिलता विश्लेषण में बहुत आम हैं। एक लघुगणक एक ऑपरेशन है, जो एक संख्या पर लागू होने पर, इसे बहुत छोटा बनाता है (जैसे वर्गमूल को लेने के लिए)। तो, पहली बात जो आपको याद रखनी चाहिए: लघुगणक मूल से कम संख्या में लौटता है। दाईं ओर की आकृति में, हरा ग्राफ रैखिक फ़ंक्शन f(n) = n , लाल f(n) = sqrt(n) , और सबसे कम तेजी से बढ़ रहा f(n) = log(n) । इसके अलावा: जिस तरह से वर्गाकार जड़ को लेना स्क्वरिंग का ऑपरेशन प्रतिलोम है, लॉगरिथम एक शक्ति के लिए कुछ बढ़ाने के उलटा ऑपरेशन है।

मैं एक उदाहरण के साथ समझाऊंगा। समीकरण पर विचार करें

2 ^x = 1024

इसमें से x को खोजने के लिए, हम खुद से पूछते हैं: 1024 प्राप्त करने के लिए आपको 2 को बढ़ाने के लिए किस डिग्री की आवश्यकता है? उत्तर: दसवें में। वास्तव में, 2 ¹⁰ = 1024 , जो सत्यापित करना आसान है। लघुगणक एक नई संकेतन का उपयोग करके इस समस्या का वर्णन करने में हमारी सहायता करते हैं। इस स्थिति में 10 1024 का लघुगणक है और इसे लॉग (1024) के रूप में लिखा जाता है। इसमें लिखा है: "लॉगरिथम 1024"। चूंकि हमने 2 को आधार के रूप में उपयोग किया है, ऐसे लॉगरिथम को "बेस 2" कहा जाता है। आधार कोई भी संख्या हो सकती है, लेकिन इस लेख में हम केवल एक ड्यूस का उपयोग करेंगे। यदि आप एक ओलम्पियाड छात्र हैं और लघुगणक से परिचित नहीं हैं, तो मेरा सुझाव है कि आप इस लेख को पढ़ने के बाद अभ्यास करें। कंप्यूटर विज्ञान में, आधार 2 लॉगरिदम किसी भी अन्य की तुलना में अधिक सामान्य हैं, क्योंकि अक्सर हमारे पास केवल दो संस्थाएं होती हैं: 0 और 1. आधे में वॉल्यूमेट्रिक कार्यों को तोड़ने की प्रवृत्ति भी होती है, और, जैसा कि आप जानते हैं, केवल दो बचे हैं। इसलिए, लेख के आगे पढ़ने के लिए, आपको केवल आधार 2 लघुगणक का विचार होना चाहिए।

व्यायाम 7

आप जो लघुगणक खोज रहे हैं, उसे नीचे लिखकर समीकरणों को हल करें। आधार 2 लघुगणक का उपयोग करें।

2 ^x = 64
(२ ^२ ) ^x = ६४
4 ^x = 4
2 ^एक्स = 1
2 ^x + 2 ^x = 32
(2 ^x) * (2 ^x ) = 64

निर्णय

ऊपर दिए गए विचारों से परे कुछ भी यहाँ की जरूरत नहीं है।

परीक्षण और त्रुटि से, हम पाते हैं कि x = 6 । तो log( 64 ) = 6
डिग्री की संपत्ति के द्वारा (2 ² ) ^x को 2 ² ^{x के} रूप में लिखा जा सकता है। इस प्रकार, हम उस 2x = 6 (क्योंकि पिछले उदाहरण से log( 64 ) = 6 प्राप्त करते हैं और इसलिए, x = 3
पिछले उदाहरण को हल करने में प्राप्त ज्ञान का उपयोग करते हुए, हम 4 को 2 ^{2 के} रूप में लिखते हैं। फिर हमारा समीकरण 2 ² ^{x के} बराबर (2 ² ) ^x = 4 में बदल जाएगा। ध्यान दें कि लॉग (4) = 2 (2 ² = 4 के बाद से), ताकि हमें 2x = 2 , व्हेंस x = 1 । मूल समीकरण से यह देखना आसान है, क्योंकि डिग्री 1 परिणाम के लिए आधार प्रदान करता है
उस डिग्री 0 को याद करने से परिणाम 1 मिलता है (यानी log( 1 ) = 0 ), हमें x = 0 मिलता है
यहां हम योग से निपट रहे हैं, इसलिए हम सीधे लघुगणक नहीं ले सकते। हालाँकि, हम देखते हैं कि 2 ^x + 2 ^x 2 * (2 ^x ) । 2 से गुणा करने पर 2 ^{x + 1} मिलता है, और हमें समीकरण 2 ^{x + 1} = 32 । हम पाते हैं कि log( 32 ) = 5 , जहां x + 1 = 5 और x = 4 ।
हम दो की दो शक्तियों को गुणा करते हैं, इसलिए, हम उन्हें 2 ^2x में जोड़ सकते हैं। यह केवल समीकरण 2 ^2x = 64 को हल करने के लिए बना हुआ है, जिसे हमने पहले ही ऊपर कर दिया है। उत्तर: x = 3

व्यावहारिक सिफारिश: प्रतियोगिताओं में, एल्गोरिदम को अक्सर C ++ में लागू किया जाता है। एक बार जब आप अपने एल्गोरिथ्म की जटिलता का विश्लेषण कर लेते हैं, तो आप तुरंत अनुमान लगा सकते हैं कि यह कितनी तेजी से काम करेगा, यह मानते हुए कि 1,000,000 निर्देश प्रति सेकंड निष्पादित होते हैं। उनकी संख्या की गणना एसिम्प्टोटिक आकलन फ़ंक्शन से की जाती है जो आपको प्राप्त हुआ था जो कि एल्गोरिथ्म का वर्णन करता है। उदाहरण के लिए, Θ (n) के साथ एल्गोरिथ्म का उपयोग करते हुए एक गणना n = 1,000,000 पर एक सेकंड लेगी।

पुनरावर्ती जटिलता

अब पुनरावर्ती कार्यों की ओर मुड़ते हैं। एक पुनरावर्ती कार्य एक फ़ंक्शन है जो स्वयं को कॉल करता है। क्या हम इसकी जटिलता का विश्लेषण कर सकते हैं? पायथन में लिखा गया निम्न कार्य किसी दिए गए संख्या के भाज्य की गणना करता है। एक सकारात्मक पूर्णांक के भाज्य को पिछले सभी सकारात्मक पूर्णांकों के उत्पाद के रूप में पाया जाता है। उदाहरण के लिए, भाज्य 5 5 * 4 * 3 * 2 * 1 । इसे "5!" के रूप में नामित किया गया है और "पाँच का भाज्य" (हालांकि, कुछ लोग "पांच !!! 11") का उच्चारण करते हैं।

 def factorial( n ): if n == 1: return 1 return n * factorial( n - 1 )

आइए इस फ़ंक्शन का विश्लेषण करें। इसमें चक्र शामिल नहीं है, लेकिन इसकी जटिलता अभी भी स्थिर नहीं है। खैर, आपको निर्देशों की गिनती फिर से करनी होगी। जाहिर है, अगर हम इस फ़ंक्शन को कुछ n लागू करते हैं, तो इसकी गणना n बार की जाएगी। (यदि आप इस बारे में निश्चित नहीं हैं, तो आप मैन्युअल रूप से गणना कर सकते हैं कि यह वास्तव में कैसे काम करता है यह निर्धारित करने के लिए n = 5 पर।) इस प्रकार, हम देखते हैं कि यह फ़ंक्शन Θ( n ) ।

यदि आप अभी भी इस बारे में निश्चित नहीं हैं, तो आप निर्देशों की संख्या की गणना करके हमेशा सटीक जटिलता पा सकते हैं। इस विधि को इस फ़ंक्शन पर लागू करें अपने f (n) को खोजने के लिए और सुनिश्चित करें कि यह रैखिक है (याद रखें कि रैखिक का अर्थ है Θ( n ) )।

लॉगरिदमिक जटिलता

कंप्यूटर विज्ञान में सबसे प्रसिद्ध कार्यों में से एक सरणी में मूल्यों की खोज करना है। हमने इसे पहले ही सामान्य मामले के लिए हल कर दिया था। यदि हमारे पास एक सॉर्ट किया गया सरणी है, जिसमें हम दिए गए मान को ढूंढना चाहते हैं, तो कार्य और अधिक दिलचस्प हो जाता है। ऐसा करने का एक तरीका द्विआधारी खोज है । हम अपने सरणी से मध्य तत्व लेते हैं: यदि यह मेल खाता है जिसे हम खोज रहे थे, तो समस्या हल हो गई है। अन्यथा, यदि दिए गए मान इस तत्व से अधिक है, तो हम जानते हैं कि यह सरणी के दाईं ओर स्थित होना चाहिए। और अगर कम है - तो बाईं ओर। जब तक हम वांछित नहीं हो जाते तब तक हम इन सबताओं को तोड़ देंगे।

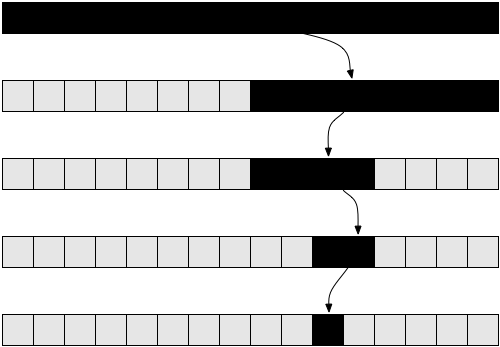
यहाँ pseudocode में ऐसी विधि का कार्यान्वयन है:

 def binarySearch( A, n, value ): if n = 1: if A[ 0 ] = value: return true else: return false if value < A[ n / 2 ]: return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value ) else if value > A[ n / 2 ]: return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value ) else: return true

दिए गए छद्म कोड वास्तविक कार्यान्वयन का एक सरलीकरण है। व्यवहार में, इस विधि को लागू करने की तुलना में वर्णन करना आसान है, क्योंकि प्रोग्रामर को कुछ अतिरिक्त मुद्दों को हल करने की आवश्यकता है। उदाहरण के लिए, एक स्थान ( ऑफ़-वन-वन एरर, ओबीओई ) द्वारा त्रुटि सुरक्षा, और दो से विभाजन हमेशा पूर्णांक नहीं दे सकते हैं, इसलिए आपको फ़ंक्शंस floor() या floor() का उपयोग करने की आवश्यकता है। हालांकि, मान लें कि हमारे मामले में, विभाजन हमेशा सफल होगा, हमारे कोड को एक-एक करके त्रुटियों से सुरक्षित किया जाता है, और हम जो करना चाहते हैं वह इस पद्धति की जटिलता का विश्लेषण है। यदि आपने पहले कभी बाइनरी खोज को लागू नहीं किया है, तो आप इसे अपनी पसंदीदा प्रोग्रामिंग भाषा में कर सकते हैं। ऐसा कार्य वास्तव में शिक्षाप्रद है।

यदि आप सुनिश्चित नहीं हैं कि विधि सिद्धांत रूप में काम करती है, तो विचलित हो जाएं और मैन्युअल रूप से कुछ सरल उदाहरण हल करें।

अब आइए इस एल्गोरिदम का विश्लेषण करने का प्रयास करें। एक बार फिर, इस मामले में हमारे पास एक पुनरावर्ती एल्गोरिदम है। आइए सादगी के लिए मान लें कि सरणी को हमेशा आधे में विभाजित किया जाता है, पुनरावर्ती कॉल में +1 और -1 भागों को अनदेखा करता है। इस बिंदु पर, आपको यह सुनिश्चित करना चाहिए कि +1 और -1 को नजरअंदाज करने जैसा छोटा परिवर्तन कठिनाई मूल्यांकन के अंतिम परिणाम को प्रभावित नहीं करेगा। सिद्धांत रूप में, इस तथ्य को साबित करने के लिए आमतौर पर आवश्यक है यदि हम गणितीय दृष्टिकोण से सावधान रहना चाहते हैं। लेकिन व्यवहार में, यह अंतर्ज्ञान के स्तर पर स्पष्ट है। इसके अलावा, सरलता के लिए, मान लें कि हमारे सरणी में दो में से किसी एक का आकार है। फिर से, यह धारणा किसी भी तरह से एल्गोरिथम की जटिलता की गणना के अंतिम परिणाम को प्रभावित नहीं करेगी। इस कार्य के लिए सबसे खराब स्थिति तब होती है जब सरणी, सिद्धांत रूप में, वांछित मान नहीं होता है। इस मामले में, हम पहले पुनरावर्ती कॉल पर n आकार का एक सरणी के साथ शुरू करते हैं, दूसरे पर n / 2 , तीसरे पर n / 4 , और इसी तरह। सामान्य तौर पर, हमारी कॉल प्रत्येक कॉल पर आधे में विभाजित होती है जब तक कि हम एकता तक नहीं पहुंच जाते। आइए प्रत्येक कॉल पर एरे में तत्वों की संख्या लिखते हैं:
0 वें पुनरावृत्ति: n
1 पुनरावृत्ति: n / 2
2 पुनरावृत्ति: n / 4
3 पुनरावृत्ति: n / 8
...
ith पुनरावृत्ति: n / 2 ⁱ
...
अंतिम पुनरावृत्ति: 1

ध्यान दें कि ith पुनरावृत्ति पर, सरणी में n / 2 ⁱ तत्व हैं। हर बार हम इसे आधा में विभाजित करते हैं, जिसका अर्थ है तत्वों की संख्या को दो से विभाजित करना (भाजक को दो से गुणा करने के बराबर)। ऐसा करने के बाद, i n / 2 ⁱ मिलता है। प्रक्रिया जारी रहेगी, और प्रत्येक बड़े से हमें एकता तक पहुंचने तक कम तत्व मिलेंगे। अगर हम यह जानना चाहते हैं कि यह क्या हुआ, तो हमें निम्नलिखित समीकरण को हल करने की आवश्यकता है:

1 = n / 2 ^मैं

समानता तभी सही होगी जब हम binarySearch() फ़ंक्शन को अंतिम कॉल पर binarySearch() , ताकि इससे सीखे i , हम अंतिम पुनरावर्ती पुनरावृत्ति की संख्या जान पाएंगे। दोनों भागों को 2 ^{i से} गुणा करने पर हमें प्राप्त होता है:

2 ^आई = n

यदि आप उपर्युक्त लघुगणक पर अनुभाग पढ़ते हैं, तो यह अभिव्यक्ति आपके लिए परिचित होगी। इसे हल करते हुए, हम प्राप्त करते हैं:

i = log( n )

यह उत्तर बताता है कि द्विआधारी खोज के लिए आवश्यक पुनरावृत्तियों की संख्या log( n ) बराबर है, जहां n मूल सरणी का आकार है।

यदि आप थोड़ा सोचते हैं, तो यह समझ में आता है। उदाहरण के लिए, n = 32 (32 तत्वों की एक सरणी) लें। एक आइटम प्राप्त करने के लिए हमें इसे कितनी बार विभाजित करने की आवश्यकता होगी? हम विचार करते हैं: 32 → 16 → 8 → 4 → 2 → 1 - कुल 5 बार, जो 32 का लघुगणक है। इस प्रकार, द्विआधारी खोज की जटिलता Θ( log( n ) ) ।

अंतिम परिणाम हमें रैखिक खोज (हमारी पिछली विधि) के साथ द्विआधारी खोज की तुलना करने की अनुमति देता है। निस्संदेह, log( n ) तुलना log( n ) बहुत छोटा है, जिसमें से यह निष्कर्ष निकालना वैध है कि पहला दूसरे की तुलना में बहुत तेज है। तो यह एरियर्स को सॉर्ट किए गए रूप में संग्रहीत करने के लिए समझ में आता है अगर हम अक्सर उनमें मूल्यों की तलाश करने जा रहे हैं।

व्यावहारिक सिफारिश: किसी प्रोग्राम के एसिम्प्टोटिक निष्पादन समय में सुधार अक्सर इसकी उत्पादकता बढ़ाता है। एक तेज प्रोग्रामिंग भाषा का उपयोग करने के रूप में एक छोटे "तकनीकी" अनुकूलन की तुलना में बहुत मजबूत।

एल्गोरिथम जटिलता विश्लेषण का परिचय (भाग 3)

लघुगणक

पुनरावर्ती जटिलता

लॉगरिदमिक जटिलता

More articles: