एल्गोरिथम जटिलता विश्लेषण का परिचय (भाग 1)

अनुवादक से: यह पाठ मामूली "संक्षिप्त रूप से" चबाने वाली सामग्री के स्थानों के कारण दिया गया है। लेखक सही चेतावनी देता है कि कुछ विषय बहुत सरल या प्रसिद्ध लगते हैं। फिर भी, मेरे लिए व्यक्तिगत रूप से इस पाठ ने एल्गोरिदम की जटिलता के विश्लेषण पर मौजूदा ज्ञान को कारगर बनाने में मदद की। मुझे उम्मीद है कि यह किसी और के लिए उपयोगी होगा।
मूल लेख की बड़ी मात्रा के कारण, मैंने इसे भागों में तोड़ दिया, जिसमें से कुल चार होंगे।
मैं (हमेशा की तरह) अनुवाद की गुणवत्ता में सुधार पर पीएम की किसी भी टिप्पणी के लिए बहुत आभारी रहूंगा।

परिचय

कई आधुनिक प्रोग्रामर जो शांत और व्यापक कार्यक्रम लिखते हैं, वे सैद्धांतिक कंप्यूटर विज्ञान का बहुत अस्पष्ट विचार रखते हैं। यह उन्हें शेष उत्कृष्ट रचनात्मक विशेषज्ञों से नहीं रोकता है, और हम जो भी बनाते हैं उसके लिए आभारी हैं।

हालांकि, सिद्धांत के ज्ञान के अपने फायदे भी हैं और यह बहुत उपयोगी हो सकता है। इस लेख में, ऐसे प्रोग्रामर का इरादा है जो अच्छे चिकित्सक हैं, लेकिन जिनके पास सिद्धांत की खराब समझ है, मैं सबसे व्यावहारिक प्रोग्रामिंग टूल में से एक पेश करूंगा: "बिग ओ" अंकन और एल्गोरिदम की जटिलता का विश्लेषण। एक व्यक्ति के रूप में, जिन्होंने शैक्षणिक विज्ञान के क्षेत्र में और व्यावसायिक सॉफ्टवेयर बनाने में दोनों काम किया है, मुझे लगता है कि ये उपकरण वास्तव में व्यवहार में उपयोगी हैं। मुझे उम्मीद है कि इस लेख को पढ़ने के बाद आप इसे और बेहतर बनाने के लिए अपने कोड पर लागू कर सकते हैं। इसके अलावा, यह पोस्ट सूचना के सिद्धांतकारों द्वारा "सामान्य ओ", "विषम व्यवहार", "सबसे बुरे मामले का विश्लेषण", आदि के रूप में उपयोग किए जाने वाले ऐसे सामान्य शब्दों की समझ के साथ लाएगा।

इस पाठ का उद्देश्य ग्रीस के हाई स्कूल के छात्रों या किसी अन्य देश में कंप्यूटर विज्ञान में अंतर्राष्ट्रीय ओलंपियाड में भाग लेना, छात्रों के लिए एल्गोरिदम में प्रतियोगिताओं और इसी तरह करना है। जैसे, इसे किसी भी जटिल गणितीय मुद्दों के पूर्व ज्ञान की आवश्यकता नहीं होती है और यह आपको एल्गोरिदम पर आगे अनुसंधान के लिए आधार प्रदान करेगा जो उनके पीछे सिद्धांत की एक ठोस समझ के साथ होगा। जैसा कि एक समय में एक व्यक्ति ने विभिन्न प्रतियोगिताओं में भाग लिया था, मैं दृढ़ता से अनुशंसा करता हूं कि आप सभी परिचयात्मक सामग्री को पढ़ें और समझें। यह ज्ञान आवश्यक होगा जब आप एल्गोरिदम और विभिन्न उन्नत तकनीकों का अध्ययन करना जारी रखेंगे।

मुझे उम्मीद है कि यह पाठ उन व्यावहारिक प्रोग्रामरों के लिए उपयोगी होगा, जिन्हें सैद्धांतिक कंप्यूटर विज्ञान में बहुत अनुभव नहीं है (यह तथ्य कि सबसे प्रेरित सॉफ्टवेयर इंजीनियर कभी कॉलेज नहीं गए थे, एक लंबे समय से रखा गया तथ्य है)। लेकिन चूंकि यह लेख छात्रों के लिए भी है, कई बार यह एक पाठ्यपुस्तक की तरह होगा। इसके अलावा, कुछ विषय आपके लिए बहुत सरल लग सकते हैं (उदाहरण के लिए, आपने अपने प्रशिक्षण के दौरान उनका सामना किया होगा)। तो अगर आपको लगता है कि आप उन्हें समझ रहे हैं, तो बस इन बिंदुओं को छोड़ दें। अन्य खंड थोड़े गहरे हैं और अधिक सैद्धांतिक हैं, क्योंकि प्रतियोगिताओं में भाग लेने वाले छात्रों को औसत चिकित्सक की तुलना में एल्गोरिथम सिद्धांत की बेहतर समझ होनी चाहिए। लेकिन इन चीजों को जानना कोई कम उपयोगी नहीं है, और कहानी के पाठ्यक्रम का पालन करना इतना मुश्किल नहीं है, इसलिए वे सबसे अधिक आपका ध्यान आकर्षित करते हैं। मूल पाठ हाई स्कूल के छात्रों को भेजा गया था, इसके लिए किसी विशेष गणितीय ज्ञान की आवश्यकता नहीं है, इसलिए प्रोग्रामिंग अनुभव वाले किसी भी व्यक्ति (उदाहरण के लिए, जो जानता है कि क्या पुनरावृत्ति है) इसे बिना किसी समस्या के समझ सकता है।

इस लेख में आपको सामग्री के लिए कई दिलचस्प लिंक मिलेंगे जो हमारी चर्चा के दायरे से परे हैं। यदि आप एक कामकाजी प्रोग्रामर हैं, तो यह संभव है कि आप इनमें से अधिकांश अवधारणाओं से परिचित हों। यदि आप सिर्फ एक शुरुआती छात्र हैं, जो प्रतियोगिताओं में भाग ले रहे हैं, तो इन लिंक पर क्लिक करने से आपको कंप्यूटर विज्ञान और सॉफ्टवेयर विकास के अन्य क्षेत्रों के बारे में जानकारी मिलेगी, जिनका आपने अभी तक अध्ययन नहीं किया है। अपने ज्ञान को बढ़ाने के लिए उन्हें ब्राउज़ करें।

"बिग ओ" अंकन और एल्गोरिदम की जटिलता का विश्लेषण ऐसी चीजें हैं जो व्यावहारिक प्रोग्रामर और नौसिखिए दोनों छात्रों को अक्सर समझने में मुश्किल, डर या आमतौर पर बचने के रूप में बेकार लगती हैं। लेकिन वे इतने जटिल और संक्षिप्त नहीं हैं क्योंकि यह पहली नज़र में लग सकता है। एल्गोरिथम जटिलता औपचारिक रूप से मापने का एक तरीका है कि कोई प्रोग्राम या एल्गोरिथ्म कितनी तेजी से काम करता है, जो एक बहुत ही व्यावहारिक लक्ष्य है। आइए इस विषय पर थोड़ी प्रेरणा से शुरू करते हैं।

प्रेरणा

हम पहले से ही जानते हैं कि ऐसे उपकरण हैं जो मापते हैं कि कोड कितनी तेजी से काम करता है। ये प्रोग्रामर कहलाते हैं जो मिलीसेकंड में निष्पादन के समय को निर्धारित करते हैं, जिससे हमें अड़चनों की पहचान करने और उन्हें अनुकूलित करने में मदद मिलती है। लेकिन, हालांकि यह एक उपयोगी उपकरण है, यह एल्गोरिदम की जटिलता से संबंधित नहीं है। एल्गोरिथ्म की जटिलता यह है कि यह एक आदर्श स्तर पर दो एल्गोरिदम की तुलना पर आधारित है, प्रोग्रामिंग भाषा के कार्यान्वयन जैसे प्रोग्राम, जिस हार्डवेयर पर चल रहा है, या इस सीपीयू में कमांड का एक सेट जैसे निम्न-स्तरीय विवरणों की अनदेखी करता है। हम एल्गोरिदम की तुलना करना चाहते हैं कि वे क्या हैं, वास्तव में: गणना कैसे होती है, इस पर विचार। मिलीसेकंड की गिनती से यहां बहुत मदद नहीं मिलेगी। यह अच्छी तरह से पता लगा सकता है कि निम्न-स्तरीय भाषा (उदाहरण के लिए, कोडांतरक ) में लिखा गया एक खराब एल्गोरिथ्म एक उच्च-स्तरीय प्रोग्रामिंग भाषा (उदाहरण के लिए, पायथन या रूबी ) में लिखे गए एक अच्छे एल्गोरिदम की तुलना में अधिक तेज़ होगा। इसलिए यह तय करने का समय है कि वास्तव में "सर्वश्रेष्ठ एल्गोरिथ्म" क्या है।

एल्गोरिथ्म एक प्रोग्राम है जो विशुद्ध रूप से कम्प्यूटेशनल है, अन्य चीजों के बिना अक्सर एक कंप्यूटर - नेटवर्क कार्यों या उपयोगकर्ता I / O द्वारा प्रदर्शन किया जाता है। एक जटिलता विश्लेषण हमें यह पता लगाने की अनुमति देता है कि यह कार्यक्रम कितनी तेजी से है जब यह गणना करता है। विशुद्ध रूप से कम्प्यूटेशनल संचालन के उदाहरण हैं फ़्लोटिंग पॉइंट नंबरों (जोड़ और गुणा) पर संचालन, रैम में स्थित डेटाबेस से दिए गए मान की खोज करना, कृत्रिम बुद्धिमत्ता (एआई) का उपयोग करके चरित्र की गति का निर्धारण करना ताकि यह खेल के अंदर थोड़ी दूरी पर ही चला जाए। दुनिया, या एक स्ट्रिंग से मिलान करने के लिए एक नियमित अभिव्यक्ति पैटर्न लॉन्च। जाहिर है, कंप्यूटर प्रोग्राम्स में कंप्यूटिंग सर्वव्यापी है।

जटिलता विश्लेषण भी हमें यह समझाने की अनुमति देता है कि इनपुट डेटा स्ट्रीम बढ़ने पर एल्गोरिदम कैसे व्यवहार करेगा। यदि हमारा एल्गोरिथ्म इनपुट पर 1000 तत्वों के साथ एक सेकंड के लिए चलता है, तो हम इस मूल्य को दोगुना करेंगे तो यह कैसे व्यवहार करेगा? क्या यह भी तेजी से काम करेगा, डेढ़ गुना तेज या चार गुना धीमा? प्रोग्रामिंग अभ्यास में, ऐसी भविष्यवाणियां बेहद महत्वपूर्ण हैं। उदाहरण के लिए, यदि हमने एक वेब एप्लिकेशन के लिए एक एल्गोरिथ्म बनाया है जो एक हज़ार उपयोगकर्ताओं के साथ काम करता है और इसके रनटाइम को मापा जाता है, तो जटिलता विश्लेषण का उपयोग करके, हम एक अच्छा विचार प्राप्त करते हैं कि क्या होता है जब उपयोगकर्ताओं की संख्या दो हज़ार तक बढ़ जाती है। एल्गोरिदम के निर्माण में प्रतिस्पर्धा के लिए, जटिलता विश्लेषण से हमें यह समझ भी मिलेगी कि इसकी शुद्धता को सत्यापित करने के लिए परीक्षण के सबसे बड़े भाग पर हमारा कोड कितने समय तक चलेगा। इसलिए, यदि हम थोड़ी मात्रा में इनपुट डेटा पर अपने प्रोग्राम के सामान्य व्यवहार को निर्धारित करते हैं, तो हम यह सोच सकते हैं कि डेटा के बड़े प्रवाह के साथ इसका क्या होगा। आइए एक सरल उदाहरण से शुरू करें: एक सरणी में अधिकतम तत्व ढूंढना।

निर्देश की गिनती

इस लेख में, मैं उदाहरणों को लागू करने के लिए विभिन्न प्रोग्रामिंग भाषाओं का उपयोग करूंगा। चिंता न करें यदि आप उनमें से किसी से परिचित नहीं हैं - जो कोई भी प्रोग्राम कर सकता है वह इस कोड को बिना किसी समस्या के पढ़ सकता है, क्योंकि यह सरल है, और मैं कार्यान्वयन भाषा के किसी भी विदेशी baubles का उपयोग नहीं करने जा रहा हूं। यदि आप एक ओलम्पियाड छात्र हैं, तो C ++ में सबसे अधिक संभावना है, इसलिए आपको कोई समस्या नहीं होनी चाहिए। इस मामले में, मैं अधिक अभ्यास के लिए C ++ का उपयोग करने की सलाह भी देता हूं।

सरणी का अधिकतम तत्व सरलतम कोड स्निपेट का उपयोग करके पाया जा सकता है। उदाहरण के लिए, एक जावास्क्रिप्ट में लिखा है। आकार n इनपुट सरणी देखते हुए:

 var M = A[ 0 ]; for ( var i = 0; i < n; ++i ) { if ( A[ i ] >= M ) { M = A[ i ]; } } 

पहले, हम गणना करते हैं कि यहां कितने मूलभूत निर्देशों की गणना की गई है। हम इसे केवल एक बार करेंगे - जैसे ही हम सिद्धांत में गहराई से जाएंगे, ऐसी आवश्यकता गायब हो जाएगी। लेकिन अभी के लिए, हम उस पर खर्च करने वाले समय के लिए धैर्य रखें। इस कोड के विश्लेषण की प्रक्रिया में, इसे सरल निर्देशों में तोड़ने का मतलब है - ऐसे कार्य जो प्रोसेसर द्वारा तुरंत किए जा सकते हैं या इसके करीब हो सकते हैं। मान लीजिए कि हमारा प्रोसेसर एक निर्देश के रूप में निम्नलिखित ऑपरेशन करने में सक्षम है:

• एक वैरिएबल के लिए एक मान असाइन करें
• किसी सरणी में किसी विशिष्ट तत्व का मान ज्ञात कीजिए
• दो मूल्यों की तुलना करें
• वेतन वृद्धि मूल्य
• बुनियादी अंकगणितीय ऑपरेशन (जैसे, जोड़ और गुणा)

हम यह मानेंगे कि शाखा ( if और if हालत की गणना के बाद कोड के else भागों के बीच चुनाव) तात्कालिक है, और हम गणना करते समय इस निर्देश को ध्यान में नहीं रखेंगे। उपरोक्त कोड में पहली पंक्ति के लिए:

 var M = A[ 0 ]; 

दो निर्देशों की आवश्यकता है: A[0] लिए खोज करने के लिए और M को एक मान निर्दिष्ट करने के लिए (हम मानते हैं कि n हमेशा कम से कम 1 है)। एल्गोरिदम द्वारा इन दो निर्देशों की आवश्यकता होगी, n के मूल्य की परवाह किए बिना। लूप के लिए भी लगातार इनिशियलाइज़ किया जाएगा, जो हमें दो और कमांड देता है: असाइनमेंट और तुलना।

 i = 0; i < n; 

यह सब पहले रन के for । प्रत्येक नए पुनरावृत्ति के बाद, हमारे पास दो और निर्देश होंगे: i वेतन वृद्धि और यह जांचने के लिए कि क्या यह हमारे लिए लूप बंद करने का समय है।

 ++i; i < n; 

इस प्रकार, अगर हम लूप बॉडी की सामग्री को अनदेखा करते हैं, तो इस एल्गोरिथ्म में निर्देशों की संख्या 4 + 2n - चार है लूप की शुरुआत में और प्रत्येक पुनरावृत्ति के लिए दो, जिनमें से हमारे पास n टुकड़े हैं। अब हम एक गणितीय फंक्शन f(n) को परिभाषित कर सकते हैं जैसे कि, n जानने के बाद, हम एल्गोरिथ्म के लिए आवश्यक निर्देशों की संख्या जानेंगे। खाली शरीर वाले लूप के लिए, f( n ) = 4 + 2n ।

सबसे खराब मामला विश्लेषण

लूप के शरीर में, हमारे पास हमेशा होने वाले सरणी और तुलनाओं में खोज अभियान होते हैं:

 if ( A[ i ] >= M ) { ... 

लेकिन if शरीर सरणी से वास्तविक मूल्य के आधार पर शुरू हो सकता है या नहीं हो सकता है। यदि ऐसा होता है कि A[ i ] >= M , तो हम दो अतिरिक्त कमांड चलाएंगे: एरे और असाइनमेंट में खोजें:

 M = A[ i ] 

हम अब आसानी से f(n) निर्धारित नहीं कर सकते हैं, क्योंकि अब निर्देशों की संख्या केवल n पर ही नहीं, बल्कि विशिष्ट इनपुट मूल्यों पर भी निर्भर करती है। उदाहरण के लिए, A = [ 1, 2, 3, 4 ] कार्यक्रम को ए = [4, 3, 2, 1] के मुकाबले अधिक कमांड की आवश्यकता होगी। जब हम एल्गोरिदम का विश्लेषण करते हैं, तो हम अक्सर सबसे खराब स्थिति पर विचार करते हैं। यह हमारे मामले में क्या होगा? एक एल्गोरिथ्म को पूरा करने के लिए सबसे अधिक निर्देशों की आवश्यकता कब होगी? उत्तर: जब एरे को आरोही क्रम में आदेश दिया जाता है, जैसे कि A = [ 1, 2, 3, 4 ] । फिर M को हर बार फिर से सौंपा जाएगा, जो टीमों की सबसे बड़ी संख्या देगा। सिद्धांतकारों के पास इसके लिए एक विचित्र नाम है - सबसे प्रतिकूल मामले का विश्लेषण , जो केवल सबसे असफल विकल्प के विचार से ज्यादा कुछ नहीं है। इस प्रकार, सबसे खराब स्थिति में, लूप के शरीर में हमारे कोड से चार निर्देश लॉन्च किए जाते हैं, और हमारे पास f( n ) = 4 + 2n + 4n = 6n + 4 ।

विषम व्यवहार

ऊपर प्राप्त फ़ंक्शन के साथ, हमारे पास एक बहुत अच्छा विचार है कि हमारा एल्गोरिथ्म कितना तेज़ है। हालांकि, जैसा कि मैंने वादा किया था, हमें लगातार इस तरह के थकाऊ काम में संलग्न होने की आवश्यकता नहीं है क्योंकि कार्यक्रम में गिनती की गई टीमें हैं। इसके अलावा, किसी विशेष प्रोसेसर के लिए उपयोग किए जाने वाले प्रोग्रामिंग भाषा के प्रत्येक प्रावधान को लागू करने के लिए आवश्यक निर्देशों की संख्या उस भाषा के संकलक और उपलब्ध निर्देश सेट (एक पर्सनल कंप्यूटर पर एएमडी या इंटेल पेंटियम, एक Playstation 2, MIPS पर आदि) पर निर्भर करती है। इससे पहले, हमने कहा कि हम इस तरह की स्थितियों को नजरअंदाज करने जा रहे हैं। इसलिए, अब हम अपने फ़ंक्शन को "फ़िल्टर" के माध्यम से पारित करेंगे ताकि इसे मामूली विवरण के रूप में साफ़ किया जा सके, जो सिद्धांतकार ध्यान देना नहीं पसंद करते हैं।

हमारे 6n + 4 फ़ंक्शन में दो तत्व होते हैं: 6n और 4 । जटिलता का विश्लेषण करते समय, केवल n में महत्वपूर्ण वृद्धि के साथ निर्देशों की गिनती के कार्य के साथ क्या हो रहा n महत्व है। यह "सबसे खराब स्थिति" के पिछले विचार के साथ मेल खाता है: हम एक एल्गोरिथ्म के व्यवहार में रुचि रखते हैं जो "बुरी परिस्थितियों" में है जब इसे कुछ कठिन करने के लिए मजबूर किया जाता है। ध्यान दें कि एल्गोरिदम की तुलना करते समय यह वास्तव में उपयोगी है। यदि उनमें से एक बड़े इनपुट डेटा स्ट्रीम के साथ दूसरे को धड़कता है, तो संभावना है कि यह तेज और हल्की, छोटी धाराओं पर रहेगा। यही कारण है कि हम फ़ंक्शन के उन तत्वों को त्याग देते हैं जो धीरे-धीरे बढ़ते n साथ बढ़ते हैं, और केवल उन लोगों को छोड़ देते हैं जो दृढ़ता से बढ़ते हैं । जाहिर है, 4 n के मूल्य की परवाह किए बिना 4 रहेगा, और 6n इसके विपरीत, बढ़ेगा। इसलिए, पहली चीज जो हम करेंगे, वह है 4 ड्रॉप और केवल f( n ) = 6n छोड़ दें।

यह 4 के बारे में सोचने के लिए समझ में आता है एक "आरंभीकरण स्थिरांक"। विभिन्न प्रोग्रामिंग भाषाओं को कॉन्फ़िगर करने के लिए अलग-अलग समय लग सकता है। उदाहरण के लिए, जावा को पहले अपनी वर्चुअल मशीन को इनिशियलाइज़ करना होगा। और जब से हम प्रोग्रामिंग भाषाओं में अंतरों को नजरअंदाज करने के लिए सहमत हुए हैं, हम बस इस मूल्य को छोड़ देंगे।

दूसरी चीज जिसे आप अनदेखा कर सकते हैं वह है n सामने का कारक। तो हमारा कार्य f( n ) = n में बदल जाता है। जैसा कि आप देख सकते हैं, यह चीजों को बहुत आसान बनाता है। यदि हम विभिन्न प्रोग्रामिंग भाषाओं (पीएल) के बीच संकलन समय में अंतर के बारे में सोचते हैं, तो एक बार फिर, यह स्थिर कारक को त्यागने का मतलब है। एक PL के लिए एक "सरणी खोज" दूसरे की तुलना में पूरी तरह से अलग संकलन कर सकता है। उदाहरण के लिए, सी में, A[ i ] को निष्पादित करना शामिल नहीं है कि i सरणी के घोषित आकार से परे नहीं जा रहा i , जबकि पास्कल के लिए यह मौजूद नहीं है। इस प्रकार, यह पास्कल कोड:

 M := A[ i ] 

C में निम्नलिखित के बराबर:

 if ( i >= 0 && i < n ) { M = A[ i ]; } 

इसलिए यह उम्मीद करता है कि विभिन्न प्रोग्रामिंग भाषाओं को विभिन्न कारकों से प्रभावित किया जाएगा जो अनुदेश गिनती को प्रभावित करेंगे। हमारे उदाहरण में, जहां हम एक "गूंगा" पास्कल संकलक का उपयोग करते हैं जो अनुकूलन के अवसरों की अनदेखी करता है, सी में एक के बजाय एक सरणी तत्व तक प्रत्येक पहुंच के लिए तीन पास्कल निर्देशों की आवश्यकता होती है। इस कारक की उपेक्षा विशिष्ट प्रोग्रामिंग भाषाओं के बीच के अंतर को अनदेखा करने की मुख्य धारा में है जैसे कि एल्गोरिथ्म के बहुत विचार का विश्लेषण करना।

ऊपर वर्णित फिल्टर - "सभी कारकों को छोड़ दें" और "केवल सबसे बड़े तत्व को छोड़ दें" - साथ में हम जो स्पर्शोन्मुख व्यवहार कहते हैं, उसे दें । f( n ) = 2n + 8 यह फंक्शन f( n ) = n द्वारा वर्णित किया जाएगा। गणित की भाषा में, हम फ़ंक्शन f की सीमा में रुचि रखते हैं, क्योंकि n अनंत तक जाता है। यदि आप इस औपचारिक वाक्यांश के अर्थ को काफी नहीं समझते हैं, तो चिंता न करें - आपको पहले से ही वह सब कुछ पता है जो आपको चाहिए। (एक तरफ: सख्ती से बोलना, गणितीय सूत्रीकरण में हम स्थिरांक को सीमा में नहीं छोड़ सकते हैं, लेकिन सैद्धांतिक सूचना विज्ञान के प्रयोजनों के लिए हम ऊपर वर्णित कारणों के लिए ऐसा करते हैं)। आइए इस अवधारणा को पूरी तरह से समझने के लिए कुछ कार्यों के माध्यम से काम करें।

हम निम्न उदाहरणों के लिए स्पर्शोन्मुख खोज करते हैं, निरंतर कारकों को त्यागने और केवल सबसे तेजी से बढ़ते तत्व को छोड़ने के सिद्धांतों का उपयोग करते हैं:

1. f( n ) = 5n + 12 f( n ) = n ।
   मैदान वही हैं जो ऊपर वर्णित हैं।
2. f( n ) = 109 f( n ) = 1 ।
   हम कारक को 109 * 1 पर छोड़ देते हैं, लेकिन 1 को दिखाने के लिए अभी भी आवश्यक है कि फ़ंक्शन शून्य नहीं है
3. f( n ) = n ² + 3n + 112 f( n ) = n ^{2 देगा}
   यहां n ² 3n से अधिक तेजी से बढ़ता है, जो बदले में, 112 से अधिक तेजी से बढ़ता है
4. f( n ) = n ³ + 1999n + 1337 f( n ) = n ^{3 देगा}
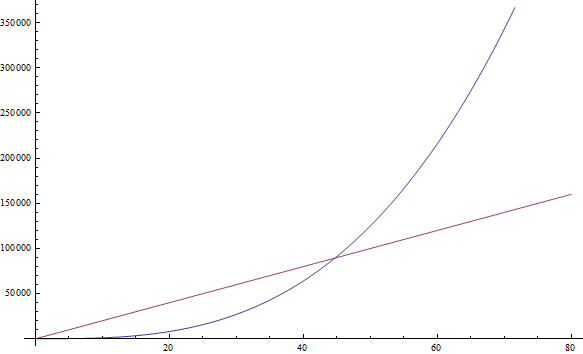
   n से पहले कारक के बड़े मूल्य के बावजूद, हम अभी भी मानते हैं कि हम और भी अधिक n पा सकते हैं, इसलिए f( n ) = n ³ अभी भी 1999n से बड़ा है (ऊपर दिया गया आंकड़ा देखें)
5. f( n ) = n + sqrt( n ) f( n ) = n
   चूँकि n बढ़ता है क्योंकि तर्क sqrt( n ) से अधिक तेज़ी से बढ़ता है