सीएफडी 3 डी: एक साधारण पानी सिम्युलेटर

परिचय

CFD (कम्प्यूटेशनल तरल गतिकी) - कम्प्यूटेशनल द्रव गतिकी।
इसका उपयोग तरल पदार्थों में विभिन्न प्रक्रियाओं को अनुकरण करने के लिए किया जाता है, साथ ही साथ विभिन्न प्रकार के तरल पदार्थ (उदाहरण के लिए, शहद, तेल - ये सभी तरल पदार्थ हैं)।

इस पोस्ट में, एक खुली सतह और बाधाओं के साथ साधारण पानी का एक 2 डी सिम्युलेटर माना जाता है (3 डी संस्करण के लिए, सब कुछ समान है + स्रोत कोड उपलब्ध हैं)।
पानी की सतह हवा से पानी को अलग करने वाली सीमा है। यह आपको लहरों, बूंदों आदि का अनुकरण करने की अनुमति देता है।

मैंने अपने सिम्युलेटर को कई कारणों से लिखने का फैसला किया। उनमें से एक इंटरनेट पर इस विषय पर ठीक से लिखे गए स्रोतों की कमी है। मुझे जो कुछ भी मिला वह या तो फोरट्रान पर था, या केवल 2 डी, या इसे समझने के लिए बहुत कठिन लिखा गया था।

तो, सिम्युलेटर की मुख्य विशेषताएं:

• वास्तविक समय मोड
• सरल और स्पष्ट गणना योजना + स्पष्ट, निहित
• खुला स्रोत
• 2d और 3 डी हैं
• में निर्मित सरल opengl प्रस्तुत करना
• xml दृश्य विवरण

गणना के संदर्भ में, मैंने नवियर-स्टोक्स समीकरणों (साथ ही इंटरनेट पर पाए जाने वाले स्रोतों से) की शुरुआत की।
यह एक चिपचिपा अपूर्ण द्रव की गति का वर्णन करने वाले आंशिक अंतर समीकरणों की एक प्रणाली है। यहाँ अतुलनीय शब्द टिक की तरह अधिक है, क्योंकि सभी तरल पदार्थ, परिभाषा के अनुसार, असंगत हैं। चिपचिपाहट का मतलब व्यक्तिगत कणों के बीच घर्षण होता है, यह उन्हें अलग-अलग दिशाओं में बिखरने से रोकता है, जैसा कि गैस के मामले में होता है, जब यह पूरी मात्रा को आवंटित करता है। तरल कण जितना संभव हो उतना एक साथ छड़ी करने की कोशिश करते हैं।

मेरे सिम्युलेटर में, मैंने समीकरणों के थोड़ा संशोधित सेट का उपयोग किया, जो उस पर अधिक ...

हाइड्रोडायनामिक समीकरण

तो, यहाँ सामान्य (वेक्टर) रूप में मूल नवियर-स्टोक्स समीकरण हैं:

यहां:

• u वेग क्षेत्र का पारंपरिक पदनाम है (2D में - वेग में x और y दिशाओं में 2 घटक होते हैं - इन्हें क्रमशः u और v द्वारा दर्शाया जाता है)
  
• p दबाव है
• टी टाइम है
• rho प्रतीक - द्रव घनत्व
• प्रतीक nu - चिपचिपाहट का गतिज गुणांक
• एफएक्सटी - तरल पदार्थ पर काम करने वाली कोई भी बाहरी ताकत, उदाहरण के लिए गुरुत्वाकर्षण (छ)

समीकरणों का पहला गति का समीकरण है, दूसरा निरंतरता समीकरण है।
गति का समीकरण न्यूटन के समीकरण मा = F के समान है, जहां हमारे दाईं ओर है - तरल पर कार्य करने वाली शक्तियों का योग - यह दबाव, प्रसार, गुरुत्वाकर्षण है ...

2 डी संस्करण के लिए, समीकरण इस फॉर्म को लेते हैं (यहां उन्हें पहले से ही एक आयामहीन रूप में प्रस्तुत किया गया है):



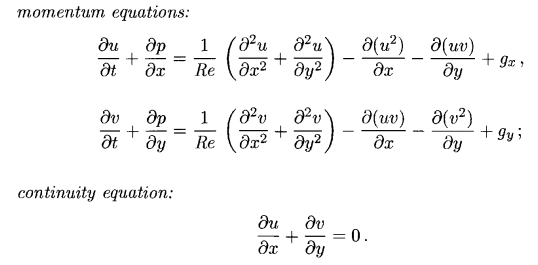
गति के समीकरण को अब 2 समीकरणों द्वारा दर्शाया गया है - 2x वेग घटकों के लिए - यू और वी।
नए गुणांक के बारे में, री रेनॉल्ड्स संख्या है (यह तब निकला जब हमने आयाम रहित चर पर स्विच किया), जो तुरंत 2 पिछले गुणांक - गुणांक को बदल देता है। घनत्व और चिपचिपाहट। यह इस बात पर निर्भर करता है कि पानी कैसा दिखेगा - जैसे शहद या साधारण पानी। जितना अधिक रे, उतना ही समान तरल साधारण पानी के लिए होता है।
कोष्ठक में, यह एक तरल (या प्रसार) के चिपचिपा व्यवहार को परिभाषित करने वाली हमारी अभिव्यक्ति है। दाईं ओर शेष शर्तें (गुरुत्वाकर्षण को छोड़कर) संवहन हैं। बाएं हिस्से में - गति और दबाव।

अगला, मैंने इन समीकरणों को थोड़ा सरल किया:



जैसा कि आप देख सकते हैं, संवहन गायब हो गया है, जो तरल के व्यवहार को थोड़ा खराब कर देता है, लेकिन पूरे पर यह नेत्रहीन सामान्य रूप से दिखता है। संवहन की अनुपस्थिति एक ही बार में कई फायदे देती है - गैर-रैखिकता गायब हो जाती है, स्थिरता में सुधार होता है और समय कदम अधिक किया जा सकता है, संवहन भी आवश्यक गणनाओं की संख्या के संदर्भ में आमतौर पर एक बहुत ही महंगा शब्द है। इसके अलावा, संवहन को ठीक से विघटित करने के लिए, विशेष योजनाओं का उपयोग किया जाता है - जो बोझिल लगता है।

समीकरणों को हल करते समय, स्प्लिटिंग नामक एक विशेष योजना का उपयोग किया जाता है। मैं इस पर अधिक विस्तार से ध्यान देना चाहूंगा, लेकिन यह एक अलग पोस्ट के लिए अधिक संभावना है। विषय काफी बड़ा है। पुस्तक में यह बहुत अच्छी तरह से वर्णित है।
संख्यात्मक सिमुलेशन के अवलोकन के तहत कंप्यूटर ग्राफिक्स के लिए Bridson R. द्रव सिमुलेशन।
और फिर तरल गतिकी में न्यूमेरिकल सिमुलेशन Griebel M Dornseifer T Neunhoeffer T SIAM 1998

यहाँ एक विभाजन समीकरण समाधान योजना है:



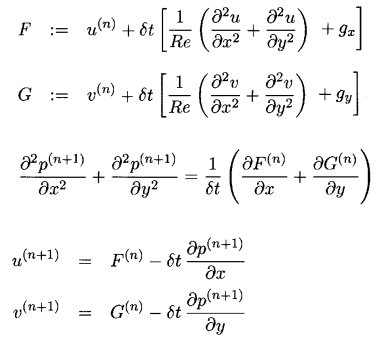
समय कदम के लिए, यूलर विधि का उपयोग किया जाता है, पहले चरण में भी हम दबाव कम करते हैं और वेगों एफ और जी की एक मध्यवर्ती गणना प्राप्त करते हैं। इन वेगों, खाते में दबाव नहीं लेने के अलावा, निरंतरता समीकरण को भी संतुष्ट नहीं करेंगे। मुश्किल जोड़तोड़ के माध्यम से, दबाव की गणना के लिए एक समीकरण पाया जाता है, जो निरंतरता समीकरण के साथ समस्या को हल करता है। पहले से गणना किए गए एफ और जी से इस समीकरण को हल करते हुए, हम एक नया दबाव पी पाते हैं।
फिर, तीसरे चरण में, गणना की गई दबाव को ध्यान में रखते हुए गति को सही किया जाता है।
यह एक पूरा समय कदम पूरा करता है और अगले चरण में सब कुछ दोहराया जाता है।

समीकरणों का विवेक

समीकरणों को अलग करने के लिए, परिमित अंतर विधि का उपयोग किया जाता है। समय कदम के लिए, मानक यूलर विधि का उपयोग किया जाता है - यह योजनाबद्ध रूप से इस तरह दिखता है: u (n + 1) = u (n) + dt * f,
जहाँ f को समीकरण के पूरे भाग के रूप में समझा जाता है जिसमें समय का अंतर शामिल नहीं होता है।

सामान्य तौर पर, समय (u (n + 1)) में एक नए पल में गति का मान पिछले समय (u (n)) के मूल्य से पाया जाता है।
मैं इस पोस्ट में समीकरणों के असतत एनालॉग्स का वर्णन नहीं करूंगा। यह तरल पदार्थ की गतिशीलता (ग्रिबेल एम डॉर्नसेफर टी नेउन्होफर टी सियाम 1998) में न्यूमेरिकल सिमुलेशन में बहुत अच्छी तरह से किया गया है।

असतत समीकरणों को हल करने के लिए, यह उपयोग किए जाने वाले समाधान की मैट्रिक्स विधि नहीं है, लेकिन पुनरावृत्त गॉस-सीडेल विधि। इसे मेट्रिसेस की प्रारंभिक असेंबली की आवश्यकता नहीं होती है और आम तौर पर किसी भी मध्यवर्ती सरणियों की आवश्यकता नहीं होती है, यह आपको गणना योजना को आसानी से संशोधित करने की अनुमति देता है, एक अनुमानित समाधान 1 पुनरावृत्ति के बाद पहले से ही है - जो पूरे सिमुलेशन को तेज करता है।

इस पोस्ट में, हम 2 डी मामले पर विचार करेंगे, मुख्य जोर सीमा शर्तों को समझाने पर होगा, क्योंकि वे समीकरणों को हल करने में सबसे बड़ी कठिनाई का कारण बनते हैं। पूरे सिम्युलेटेड क्षेत्र को क्षैतिज और जमैक्स को लंबवत रूप से इमैक्स पॉइंट में विभाजित किया गया है। यह इमैक्स * जेमैक्स कोशिकाओं का एक ग्रिड बन जाता है।
4 सीमाओं से उनके लिए सीमा बिंदु जोड़े जाते हैं। कुल में, आकार का एक सरणी (imax + 2) * (jmax + 2) प्राप्त किया जाता है।

प्रत्येक कोशिका के वेग और दबाव के अपने मूल्य हैं - यह वेक्टर वेग क्षेत्र और कम्प्यूटेशनल ग्रिड पर स्केलर दबाव क्षेत्र के बारे में बात करने के लिए प्रथागत है।
यू सेल में कण वेग x है
V, कोशिका में y में कण वेग है
पी - दबाव

यह आमतौर पर कोशिकाओं के केंद्र में गणना किए गए चर (यू, वी, पी) की व्यवस्था करने के लिए प्रथागत है, लेकिन द्रव मॉडलिंग के मामले में यह हमेशा समाधान के साथ समस्याओं का कारण बनता है - यह पूरी तरह से सही नहीं है और दोलन करता है। इसलिए, सीएफडी एक कंपित ग्रिड का उपयोग करता है - इसे लीपफ्रॉग भी कहा जाता है।



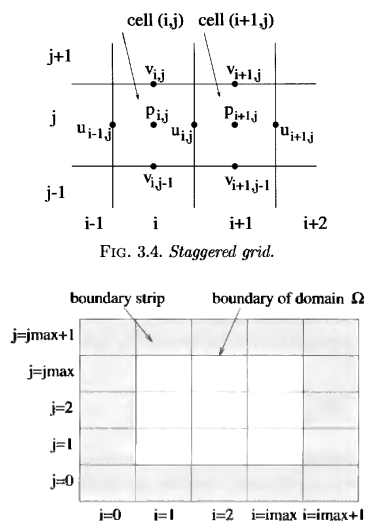
यह आंकड़ा से देखा जा सकता है कि वेग कोशिका में ही नहीं बल्कि उसके चेहरे पर, यू - सेल की दाईं सीमा पर, और v - ऊपरी सीमा पर हैं।

दीवारों पर सीमा की स्थिति

परिमित अंतर विधि द्वारा गणना करने के लिए, हमें कम्प्यूटेशनल ग्रिड की सीमाओं पर मान (यू, वी, पी) निर्धारित करने की आवश्यकता है। ये 4 दीवारें हैं - बाएं से नीचे और ऊपर से दाईं ओर। सीमा की स्थिति बिना पर्ची और मुफ्त-नींद के प्रकार की हो सकती है; अन्य प्रकार हैं, लेकिन ये सामान्य योजना के बजाय अधिक विशिष्ट स्थितियां हैं।

फ्री-स्लीप - इसका मतलब है कि तरल दीवार के साथ स्वतंत्र रूप से ग्लाइड करता है, जैसे कि कोई घर्षण नहीं है और कुछ भी इसके साथ आगे बढ़ने से रोकता है।
इस पोस्ट में हम इस प्रकार की सीमा शर्तों पर विचार नहीं करते हैं।

नो-स्लिप एक चिपकी स्थिति है - अर्थात, जब कोई दीवार टकराती है, तो एक द्रव धीमा हो जाता है।
इसका मतलब है कि द्रव वेग दीवार के वेग के साथ मेल खाता है (अर्थात, हमारे मामले में यह एक निश्चित सीमा पर शून्य के बराबर है)।

उदाहरण के लिए, केवल सही सीमा पर विचार करें: वेग का u घटक = 0, क्योंकि यह दीवार के लिए लंबवत है और पानी को सीमा में प्रवेश नहीं करना चाहिए।
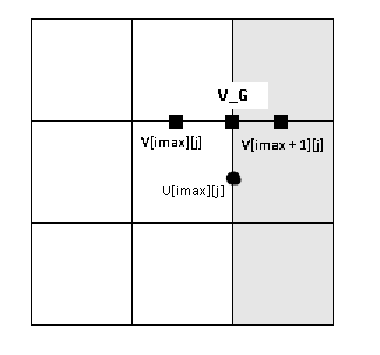
नो-स्लिप सीमा के मामले के लिए v घटक भी 0 है, लेकिन हमारे कंपित जाल के लिए इसे सही करना होगा। v घटक के लिए, यह देखते हुए कि v सीधे सीमा पर नहीं है, आपको अभिव्यक्ति को थोड़ा ठीक करने की आवश्यकता है।
दीवार पर v अंतिम 2 कोशिकाओं के बीच औसत के बराबर होगा। v_g = (v [imax + 1] [j] + v [imax] [j]) / २
v_g शून्य के बराबर है ((v [imax + 1] [j] + v [imax] [j]) / 2 = 0) और हम यहाँ से मान v [imax + 1] [j] पाते हैं, जिसे हमें प्रोग्राम में सेट करने की आवश्यकता है:
v [इमैक्स + 1] [जे] = - वी [इमैक्स] [जे];
ऊपरी सीमा पर यू घटकों के लिए एक ही चीज की आवश्यकता है।



4 बॉर्डर्स को निम्न निर्देशांक द्वारा सरणी में दर्शाया गया है:

बाईं दीवार

यू [०] [जे], जहां जे पूरी दीवार पर चलता है
v [०] [जे]

यहाँ कोड में ऐसा दिखता है:

for (j = 0; j <= jmax + 1; j++) { U[0][j] = 0.0; V[0][j] = -V[1][j]; } 

नीचे की दीवार

u [i] [०]
v [i] [०]

 for (i = 0; i <= imax + 1; i++) { U[i][0] = -U[i][1]; V[i][0] = 0.0; } 

दाहिनी दीवार
चूँकि हमारे पास एक स्पाईड ग्रिड है, दाईं दीवार पर हमारे पास u के मानों के लिए एक बॉर्डर है जो अंतिम कॉलम के साथ नहीं बल्कि पास से गुजरता है - इसलिए, हम U के लिए सेल में U [imax] [j] के लिए मान सेट करते हैं।

यू [इमैक्स] [जे]
v [इमैक्स + 1] [जे]

 for (j = 0; j <= jmax + 1; j++) { U[imax][j] = 0.0; V[imax + 1][j] = -V[imax][j]; } 

शीर्ष दीवार
यहाँ, v के मानों के लिए, सीमा पारगम्य रेखा के साथ चलती है - jmax - इसलिए हम V के लिए मान को सेल में सेट करते हैं - V [i] [jmax]

u [i] [jmax + 1]
v [i] [jmax]

 for (i = 0; i <= imax + 1; i++) { U[i][jmax + 1] = -U[i][jmax]; V[i][jmax] = 0.0; } 

मुख्य सॉल्वर का परीक्षण करने के लिए, आप सभी सीमा मान = 0 सेट कर सकते हैं।

हमें दबाव को सीमाओं पर रखने की भी आवश्यकता है। दबाव को कोशिकाओं के केंद्र में सेट किया जाता है और किनारों पर गति के रूप में नहीं। इसलिए, यह बहुत सरल है। सीमाओं पर दबाव को उसी तरह सेट किया जा सकता है जैसे पड़ोसी कोशिकाओं में। बस पड़ोसी कोशिकाओं से मूल्यों की प्रतिलिपि बनाएँ।

 for (j = 1; j <= jmax; j++) { //   P[0][j] = P[1][j]; //   P[imax + 1][j] = P[imax][j]; } for (i = 1; i <= imax; i++) { P[i][0] = P[i][1]; P[i][jmax + 1] = P[i][jmax]; } 

बाधाओं पर सीमा की स्थिति

ध्वज C_B द्वारा बाधाओं का प्रतिनिधित्व किया जाता है। उनके लिए सीमा की स्थिति बाहरी दीवारों के समान सिद्धांत पर निर्धारित की जाती है। मैं दबाव स्थापित करने के 2 उदाहरण दूंगा:

 if (IsObstacle(i, j)) { //     -  -    P   if (IsFluid(i, j - 1)) { P[i][j] = P[i][j - 1]; } //   -  ... else if (IsFluid(i - 1, j)) { P[i][j] = P[i - 1][j]; } // ....... } 

एक कोणीय कोशिका के लिए, हम आसपास के जल कोशिकाओं के मूल्यों का औसत लेते हैं। उदाहरण के लिए, एक बाधा लें, इसके बाईं ओर और ऊपर पानी होगा। तब हम बाधा कोशिका में दबाव को निम्नानुसार मानते हैं:

 if (IsFluid(i - 1, j) && IsFluid(i, j + 1)) { P[i][j] = (P[i][j + 1] + P[i - 1][j]) / 2; } 

सतह पर सीमा की स्थिति

सतह और इसकी गति कणों का उपयोग करके मॉडलिंग की जाती है। (इस खंड में वर्णित सतह पर सीमा की स्थिति वाले स्रोत, सरलतम बाधा फ़ोल्डर में हैं।)

प्रारंभ में, कणों को तरल के साथ कोशिकाओं में रखा जाता है, प्रति सेल 4 टुकड़े (प्रत्येक कोने के पास 1)। अगला, प्रत्येक चरण में कण शास्त्रीय यांत्रिकी से सरल यूलर विधि का उपयोग करके चलते हैं। गति के लिए गति को प्रत्येक कोशिका में पूरे सेल के लिए औसत के रूप में लिया जाता है (हालांकि इसका उपयोग करने के लिए कोई समस्या नहीं है, उदाहरण के लिए, इंटरपोल)।

  x = particles[k].x; y = particles[k].y; //        i = (int)(x / delx); j = (int)(y / dely); u = U[i][j]; v = V[i][j]; //        x += delt * u; y += delt * v; 

प्रत्येक चरण पर, कणों वाले कोशिकाओं को पानी के रूप में लेबल किया जाता है। बाकी खाली कोशिकाएं हैं, उनमें मूल चर (u, v, p) की गणना नहीं की जाती है।

मुख्य चर की गणना करने के लिए, सतह और आसन्न कोशिकाओं पर सीमा की स्थिति निर्धारित करना आवश्यक है, जैसे कि दीवारों के लिए आवश्यक था। लेकिन पहले आपको यह निर्धारित करने की आवश्यकता है कि कौन से सेल, पानी के रूप में लेबल किए गए हैं, सतह के हैं, और यह भी कि हवा किस तरफ से है। इन उद्देश्यों के लिए, 2 सरणियों का उपयोग किया जाता है - FLAG और FLAGSURF। पहले में, केवल सेल प्रकार निर्दिष्ट किए जाते हैं - जल, वायु (खाली) और बाधाएं। यहाँ संगत झंडे हैं (संक्षिप्त बी - सीमा एफ - द्रव ई - खाली):

 public const int C_B = 0x0000; // public const int C_F = 0x0010;// public const int C_E = 0x1000;// 

FLAGSURF सरणी का उपयोग सतह कोशिकाओं को निर्धारित करने के लिए किया जाता है, शेष कोशिकाओं के लिए, मूल्य = 0। इस सरणी में झंडे न केवल सेल के प्रकार, बल्कि पड़ोसी कोशिकाओं के सभी संयोजनों को निर्धारित करते हैं जिसमें यह खाली है। झंडे को मानक बिट मास्क के रूप में बनाया जाता है ताकि उन्हें संयोजित किया जा सके।
FLAGSURF में प्रत्येक मान में 4 बिट्स होते हैं जो 4 पक्षों (आसन्न कोशिकाओं) के अनुरूप होते हैं।
यदि बिट 1 पर सेट है, तो संबंधित पड़ोसी सेल में - खाली। अगर 0 - तो पानी है।
बिट्स: 0000 एनएसडब्ल्यूओ 0000 0000 - अक्षर एन (उत्तर उत्तर) एस (दक्षिण दक्षिण) डब्ल्यू (पश्चिम पूर्व) और ओ (पश्चिम) के 4 पक्षों को इंगित करते हैं।

झंडे की पूरी सूची स्रोत में है, इसलिए मैं मूल्यों के केवल कुछ उदाहरण दूंगा:

public const int C_W = 0x0200; // 512
बाइनरी में, मान 0000 0010 0000 0000 जैसा दिखता है
यहाँ साइड W से संबंधित ध्वज 1 पर सेट है। इसका मतलब है कि वर्तमान सेल के बाईं ओर खाली है।
इसी समय, शेष 3 बिट्स 0 पर सेट होते हैं, जिसका अर्थ है कि शेष पड़ोसी कोशिकाएं पानी से भर जाती हैं।



पब्लिक कास्ट int C_SW = 0x0600; // 1536 0000 0110 0000 0000
यहाँ W और S के किनारों पर संबंधित ध्वज 1 पर सेट है। तो वर्तमान सेल के बाईं और नीचे खाली है, और शेष सेल पानी हैं



सतह की कोशिकाओं के प्रकार का निर्धारण और FLAGSURF सरणी में भरने के दौरान, संबंधित बिट्स को इस तरह से 1 पर सेट किया जाता है:

 //   ,      1 if (FLAG[i-1][j] == GG.C_E) FLAGSURF[i][j] = FLAGSURF[i][j] | GG.C_W; 

FLAGSURF सरणी को मुख्य रूप से केवल सतह पर सीमा की स्थिति स्थापित करने की सुविधा के लिए आवश्यक है। चूंकि विभिन्न प्रकार की सतह कोशिकाओं के लिए अलग-अलग सीमा स्थितियां लागू होती हैं। जैसा कि पहले ही उल्लेख किया गया है, हमें सतह कोशिकाओं के बगल में खाली कोशिकाओं में सीमा की शर्तों को नीचे रखने की आवश्यकता है और सतह की कोशिकाओं में भी सीमा की स्थिति की आवश्यकता है, क्योंकि हमारे पास एक कंपित ग्रिड है और सभी सतह कोशिकाएं यूवी चर की गणना में शामिल नहीं हैं।

मूल्यों को स्थापित करने का सिद्धांत सरल है। क्योंकि हवा का दबाव पानी में दबाव से 1000 गुना कम है - इसे उपेक्षित किया जा सकता है और पानी को सतह के साथ स्वतंत्र रूप से स्थानांतरित करने की अनुमति दी जाती है, इसकी गति को सीमित किए बिना और आंदोलन की दिशा को बदले बिना। बेशक, मेरी योजना में सतह के तनाव को ध्यान में नहीं रखा गया है, अन्यथा सब कुछ बहुत अधिक जटिल होता।

हम सतह कोशिकाओं में रिक्त स्थान यू और वी के मूल्यों और उन्हें खाली करने वाली खाली कोशिकाओं को नीचे रख देते हैं, यह भूलकर कि हमारे पास एक कंपित ग्रिड है।
प्लेसमेंट के लिए मान पड़ोसी पानी की कोशिकाओं से लिया जाता है। यह केवल यह तय करने के लिए रहता है कि किस पड़ोसी से यह सब लिया गया है, क्योंकि ऐसी कई कोशिकाएँ हो सकती हैं।



यहां एक स्क्रीन है जिसमें सीमा की स्थिति है, जिसे आपको चिपकाए जाने की आवश्यकता है। नीले वर्ग पानी हैं। काले निशान आवश्यक सीमा शर्तें हैं। ध्यान दें कि लेबल सतह की कोशिकाओं में और आंशिक रूप से खाली कोशिकाओं में आंशिक रूप से स्थित हैं। ऐसा इसलिए होता है क्योंकि सॉल्वर कोड में हमारे पास ऐसी स्थितियां होती हैं (जैसा कि आप देख सकते हैं, यूवी की गणना सही सीमा की दीवार के सामने की कोशिकाओं में नहीं की जाती है):

  if (IsFluid(i, j) && IsFluid(i+1, j)){ F[i][j] = ... } 

आइए कुछ उदाहरण देखें:

झंडा पिंजरा C_SW

  case GG.C_SW: { U[i][j - 1] = U[i][j]; V[i][j - 1] = V[i][j]; U[i - 1][j] = U[i][j]; V[i - 1][j] = V[i][j]; } break; 

यहां हमें सेल में स्वयं मानों की आवश्यकता नहीं है - उनकी गणना सॉल्वर में की जाएगी। लेकिन फिर हमें पड़ोसी खाली कोशिकाओं में मूल्यों की आवश्यकता है - क्योंकि सॉल्वर में U [i] [j - 1] इत्यादि शब्द होते हैं।

इन खाली कोशिकाओं के लिए निकटतम जल कोशिका कोशिका [i] [j] है और इसमें से U और V के मान लिए जाते हैं
यह आंकड़ा से देखा जा सकता है कि V [i - 1] [j] का मान सेल [i] [j] और [i - 1] [j + 1] से लिया जा सकता है, लेकिन सामान्य स्थिति में, सेल [] i - 1] [j + 1] गैर-जल हो सकता है, और इसमें V का मान भी सीमा से बाहर हो सकता है और अभी तक नीचे नहीं डाला जाएगा। इसलिए, सही विकल्प [i] [j] है क्योंकि इसमें मानों की गणना सॉल्वर में की जाएगी। ।

झंडा पिंजरा C_W

  case GG.C_W: { U[i - 1][j] = U[i][j]; V[i - 1][j] = V[i][j]; } break; 

यहां सब कुछ समान है।

ध्वज C_NW के साथ सेल

  case GG.C_NW: { V[i][j] = V[i][j - 1]; U[i - 1][j] = U[i][j]; } break; 

यहां, सेल में यू के मूल्य की गणना सॉल्वर में ही की जाएगी, क्योंकि उसके दाईं ओर एक पानी का कक्ष है। लेकिन वी को नीचे रखने की जरूरत है, क्योंकि शीर्ष पर सेल खाली है। यू [i] [जे] की गणना के बाद से मूल्य यू [i - 1] [जे] को सेट करना भी आवश्यक है, पड़ोसी कोशिकाओं में मूल्यों की भी आवश्यकता होगी, जिसमें शामिल हैं यू [i - 1] [जे]।

उसी तरह जैसे पिछले मामले में, हम सेल V [i] [j - 1] से V [i] [j] का मूल्य लेते हैं, और V [i-1] से [j] - V [i-१ में मान नहीं लेते हैं। ] [जे] सीमा हो सकती है और अभी तक ज्ञात नहीं है।

हम खाली कोशिकाओं और सतह कोशिकाओं में दबाव सेट करते हैं = 0. यह पूरी तरह से सही नहीं है, लेकिन यह काम करता है।
सतह कोशिकाओं में, दबाव आवश्यक है, क्योंकि दबाव के लिए समीकरण को हल करते समय, ये कोशिकाएं सीमा होती हैं और दबाव गणना सीधे उन में नहीं की जाती है।

कण-केवल द्रव गति एल्गोरिथ्म

स्रोत में शीर्षक में नाम ट्रैक के साथ विकल्प हैं। यह एक स्वतंत्र सतह को स्थानांतरित करने की एक विधि है जिसमें कण केवल सतह पर ही चलते हैं, और तरल की पूरी मात्रा में नहीं। यह कुछ हद तक वीओएफ पद्धति के समान है - लेकिन सतह का प्रारंभिक पुनर्निर्माण वहां किया जाता है, जो कि बोझिल है। मेरी विधि में, यदि कोई कण किसी सेल को छोड़ता है, तो इसे खाली चिह्नित किया जाता है, और कणों को पास के तरल कोशिकाओं में जोड़ा जाता है जिसमें कोई कण नहीं होते हैं - यह जानने के लिए कि सतह कहां है। यदि कण एक खाली सेल में गुजरता है, तो सेल को तरल के रूप में चिह्नित किया जाता है। बेशक, इस पद्धति में अशुद्धि का एक सभ्य हिस्सा है, लेकिन यह तेज है और जटिल कोडिंग की आवश्यकता नहीं है।

अधिनिर्णय गणना योजना

स्रोतों में सॉल्वर का एक निहित संस्करण भी है - यह गति के समीकरणों पर लागू होता है, स्पष्ट संस्करण से कोड में अंतर कम से कम हैं। जब नमूना, बस यू और वी के साथ सभी शर्तें [i] [जे] समीकरण के बाईं ओर जाएं और दाईं ओर के रूप में नहीं। स्पष्ट (निहित) योजना आपको बहुत बड़े समय के कदम उठाने की अनुमति देती है, जो स्पष्ट के साथ असंभव है।
आप यहाँ http://math.mit.edu/cse/codes/mit18086_navierstokes.pdf के बारे में पढ़ सकते हैं।

3 डी संस्करण

3 डी संस्करण में, सब कुछ 2 डी के साथ सादृश्य द्वारा किया जाता है।
कैमरे को घुमाने के लिए F1-F8 + WASD कीज़, एरो और ER PgUp PgDown को कंट्रोल करता है।
पानी के स्रोत के साथ दृश्यों के लिए - पी कुंजी - पानी के दबाव को बंद करने के लिए।
जी - बेहतर सतह प्रतिपादन (क्यूब्स के बजाय गोले का उपयोग किया जाता है), लेकिन यह बहुत धीमा हो जाता है।
डेमोस फ़ोल्डर में - xml फ़ाइल के रूप में दृश्य और पैरामीटर (आकार, समय कदम, गुरुत्वाकर्षण और प्रति सेल कणों की संख्या) होते हैं। अपने हाइटपैप (हाइट्स का नक्शा) को पेंट में पेंट करना भी संभव है, आकार किसी भी हो सकते हैं - ऑटोरेस्ज़ हैं।

अंत में, मैं 2D और 3D से स्क्रीनशॉट दूंगा:







स्रोत यहां स्रोत हैं।





PS यदि सीएफडी से परिचित लोग हैं, तो समाधान की गति और शुद्धता के संदर्भ में एक साथ इस परियोजना को बेहतर बनाना दिलचस्प होगा (विशेषकर जब सतह को मॉडलिंग करते हैं)।
मैं खुद कमोबेश प्रतिपादन प्रस्तुत कर सकता हूं, लेकिन गणित और भौतिकी मेरा मुख्य क्षेत्र नहीं है। मुझे किसी भी टिप्पणी और उपयोगी सुझाव पर खुशी होगी।