🧓🏻 🤾🏿 🥣 लिनक्स के लिए 1k / 4k इंट्रो बनाना, भाग 4 👩🏾‍🏭 🚨 🧖

ऑल द बेस्ट, मेरे अति धैर्यवान मित्रों!
जैसा कि आप में से बहुत से लोग याद करते हैं, दूसरे भाग में हम इस तथ्य पर रुक गए थे कि हमें वहाँ कुछ सौ बाइट्स की पूरी स्क्रीन पर एक आयत मिली थी, और अब डेढ़ साल के लिए हमें रचनात्मकता के साथ अपने कोड और दिलों में शून्य भरने की समस्या का सामना करना पड़ा है।

आखिरकार, सिर्फ दो त्रिकोणों के साथ क्या खींचा जा सकता है? स्क्वायर? भग्न? सिटी सेंटर में मेगाटन पावर विस्फोट के माध्यम से उड़ान? क्या पागलपन की कोई सीमा है, जहां वास्तविकता समाप्त होती है और वास्तविकता शुरू होती है? किरणों की ठीक से देखभाल कैसे करें, उन्हें कैसे खिलाना है और किस चीज के बारे में प्रतिबिंबित करना है, आप अचानक से लेख के सिलसिले में जानेंगे!

परिचय

प्रोटोटाइप की सुविधा के लिए, मैं shadertoy.com का उपयोग करने का सुझाव देता हूं , उदाहरणों के साथ लिंक वहां ले जाएंगे। इस प्रकार, यहां तक कि वैकल्पिक ऑपरेटिंग सिस्टम के उपयोगकर्ता भी इस सभी अद्भुत में खुद को विसर्जित कर सकते हैं जो यहां होगा।
हां, विंडोज वेबएल के लिए, जिसका हम स्पष्ट रूप से उपयोग करेंगे, किसी कारण से हर कोई इसे ANGLE के माध्यम से लागू करना पसंद करता है, जो एक व्यसनी है और जटिल शेड्स को लॉक करने के लिए प्रसिद्ध है। इसलिए, मैं सुझाव देता हूं कि आप देशी ओपनगैल (क्रोम में: --use-gl = डेस्कटॉप पर स्टार्टअप) को सक्षम करें, अन्यथा तीसरे या चौथे उदाहरण के बाद, सब कुछ विस्फोट हो जाएगा और शायद ही चर्चा के अनुरूप होगा।
और हां, हमें काफी शक्तिशाली आधुनिक वीडियो कार्ड की आवश्यकता है, कुछ कम से कम GTX 4xx या HD 6xxx की तरह (और इंटेल का कोई मतलब नहीं है, क्या हंसना है), अन्यथा एक फिल्मस्ट्रिप होगी।

परिचय 2

मुझे इस बारे में ब्योरा नहीं है कि वे क्या हैं, कहां से आए हैं और क्यों - यह लेखों की एक अलग श्रृंखला के लिए एक विषय है, जो मौजूद नहीं होगा, योग्य - यह समझने के लिए पर्याप्त है कि हमें वर्तमान gl_FragColor रंग वैरिएबल gl_FragColor के सिंटैक्स के आधार पर gl_FragColor इसके निर्देशांक gl_FragCoord (पिक्सेल में) और iGlobalTime समय हैं (यह एक shader विशिष्टता है, GLSL मानक में, निश्चित रूप से, समय के बारे में कुछ भी नहीं है)।
GLSL में, अन्य बातों के अलावा, वेक्टर और मैट्रिक्स प्रकार vecN , matN और गणितीय के सभी प्रकार के एक मानक पुस्तकालय हैं और ऐसा नहीं है। जिज्ञासु के लिए Href (GL ES क्योंकि शेडर WebGL है, जो OpenGL ES 2.0 से विरासत में मिला है)।

रीयलटाइम रीट्रैक्टिंग

मैं वह करने का प्रस्ताव करता हूं जो 10-15 साल पहले एक अप्राप्य सपना माना जाता था - वास्तविक समय में किरण अनुरेखण। आधुनिक वीडियो कार्ड इतने राक्षसी रूप से उत्पादक हैं कि हां।
मुख्य विचार स्क्रीन पर एक पिक्सेल के रंग का निर्धारण करना है, इसमें से एक किरण शुरू करें और देखें कि वह किस वस्तु के खिलाफ आराम करेगा, जिसके बाद वस्तु और ज्ञान बिंदु के ज्ञान का उपयोग करके हम किसी तरह रोशनी की गणना करते हैं और वांछित रंग बनाते हैं।
मैं कैसे निर्धारित कर सकता हूं कि कोई किरण किसी निश्चित वस्तु को पार करती है, और यदि हां, तो किस बिंदु पर है? उदाहरण के लिए, वांछित वस्तु के साथ किरण के प्रतिच्छेदन के समीकरणों को लिखना और उन्हें विश्लेषणात्मक रूप से हल करना संभव है। यह पता लगाना आसान है कि यह विधि बहुत जल्दी एक क्षेत्र या विमान से अधिक जटिल कुछ के लिए काफी बोझिल हो जाती है। यह अच्छा नहीं है, हम मंगल ग्रह पर एक बिल्ली के पैक की लैंडिंग को आकर्षित करना चाहते हैं, इसलिए हम दूरी के कार्यों का एक और तरीका, अर्थात् गोलाकार अनुरेखण का उपयोग करेंगे।

मुझसे तुम तक

दूरी फ़ंक्शन एक R3-> R फ़ंक्शन है जो अंतरिक्ष में प्रत्येक बिंदु के लिए निकटतम ज्यामिति की दूरी देता है। व्यवहार में, साधारण आंकड़ों के लिए भी ऐसे कार्य लिखना विश्लेषणात्मक चौराहे की तुलना में आसान है। उदाहरण के लिए:

गेंद: length(at) - R
विमान: dot(at,N) - D
length(max(abs(at)-size), 0.)) : length(max(abs(at)-size), 0.))
सिलेंडर (Y): length(at.xz) - R

इसके अलावा, ऐसे कार्यों का उपयोग करके रचनात्मक ज्यामिति बनाना आसान है:

गठबंधन: min(f, g)
प्रतिच्छेदन: max(f, g) *
घटाव: max(f, -g) *

और रूपांतरण - यह इनपुट सैंपलिंग वेक्टर को बदलने के लिए पर्याप्त है:

कैर्री: at-vec3(pos)
रोटेशन और इसी तरह: at*mat3(< >) (स्केलिंग के लिए, ध्यान रखें कि वापसी की दूरी को वापस बढ़ाया जाना चाहिए)

* - सख्त एफ-दूरी और एक अनुमान नहीं है

गोलाकार निशान

इस तरह के एक फ़ंक्शन के साथ बीम के चौराहे को कैसे ढूंढें? एक सरल और सुरुचिपूर्ण समाधान गोलाकार अनुरेखण है। एल्गोरिथ्म इस प्रकार है:

हम बीम को बिंदु O से दिशा D में शुरू करते हैं।
हम बिंदु O पर फ़ंक्शन के मान के बराबर घ आते हैं
बिंदु D को दिशा D में दूरी d से स्थानांतरित करें
यदि d कुछ चयनित थ्रेशोल्ड मान से अधिक है, तो हम चरण 2 पर लौटते हैं
वर्तमान बिंदु ओ एक निश्चित सटीकता के साथ वांछित चौराहा है, हम बाहर निकलते हैं

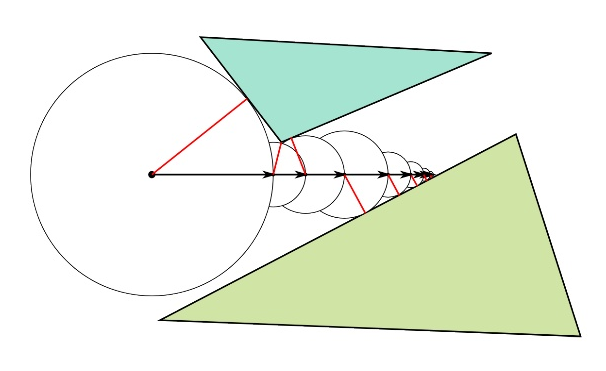
GLSL पर, एक सरल ट्रेस फ़ंक्शन इस तरह दिखता है:

 float trace(vec3 O, vec3 D) { float L = 0.; for (int i = 0; i < MAX_STEPS; ++i) { float d = world(O + D*L); L += d; if (d < EPSILON) break; } return L; }

कुल मिलाकर, मूल रूप में 1 के त्रिज्या के साथ एक क्षेत्र के लिए एक साधारण मार्चर, उदाहरण के लिए, इस तरह (दूरी की यात्रा का दृश्य):

 // ,      #define MAX_STEPS 32 #define EPSILON .001 //         float world(vec3 a) { return length(a) - 1.; //   1   } //      O    D.    float trace(vec3 O, vec3 D) { float L = 0.; //   for (int i = 0; i < MAX_STEPS; ++i) { //  MAX_STEPS  float d = world(O + D*L); //      L += d; //     if (d < EPSILON*L) break; //     ,  } return L; //    } void main(void) { //     [-1., 1.] vec2 uv = gl_FragCoord.xy / iResolution.xy * 2. - 1.; //     uv.x *= iResolution.x / iResolution.y; //   vec3 O = vec3(0., 0., 3.); //      z ; -2.       -  vec3 D = normalize(vec3(uv, -2.)); //    float path = trace(O, D); //  ,    gl_FragColor = vec4(path * .2); }

हमारा गोला संदिग्ध रूप से हवा में लटका हुआ है, तो आइए इसे एक विमान पर रखें, उदाहरण के लिए:

 float world(vec3 a) { return min(length(a) - 1., ay + 1.); }

अब चकाचौंध और तामझाम के बिना, एक सरल फैलाना शुरू करने के लिए, प्रकाश को हिलाएं।
सरल लैंबर्ट मॉडल में, यह माना जाता है कि सतह पर प्रकाश की घटना सभी दिशाओं में समान रूप से बिखरी हुई है, और इसलिए बिंदु का प्रकाश सामान्य स्रोत और प्रकाश स्रोत की दिशा के बीच कोण के कोसाइन के लिए आनुपातिक है। इसके अलावा, रोशनी स्रोत से दूरी के एक वर्ग के रूप में घट जाती है। खैर, आपको स्रोत और सतह के रंगों के बारे में नहीं भूलना चाहिए।
कोड में, यह कुछ इस तरह दिखता है:

 vec3 enlight(vec3 at, vec3 normal, vec3 diffuse, vec3 l_color, vec3 l_pos) { //        vec3 l_dir = l_pos - at; //  =      //  =   (=   ) //        (=   ) //       ,         return diffuse * l_color * max(0.,dot(normal,normalize(l_dir))) / dot(l_dir, l_dir); }

यह सामान्य होना आसान है - यह हमारी दूरी के कार्य का केवल ढाल है:

 vec3 wnormal(vec3 a) { vec2 e = vec2(.001, 0.); float w = world(a); return normalize(vec3( world(a+e.xyy) - w, world(a+e.yxy) - w, world(a+e.yyx) - w)); }

परिणाम:

कुछ याद आ रहा है, है ना? गोला अभी भी लटका हुआ है, और किसी तरह अंधेरा है।
आंखों को पूरी तरह से यथार्थवादी और सुखद होने के लिए, दो चीजों को जोड़ा जाना चाहिए: एक छाया और एक गिलास छाया।

सबसे पहले, अपने रंग में अपने स्वाद के लिए vec3(.1) या .2 जैसी किसी चीज़ को जोड़कर एम्बींट लाइटिंग डालें।
कप छाया, परिवेशीय रोड़ा भी, वास्तविक दुनिया से प्रभाव का एक अनुमान है, जब सतह को सभी पक्षों से उड़ान भरने वाले फोटोन द्वारा आंशिक रूप से अस्पष्ट किया जाता है, और न केवल प्रकाश स्रोत से।
वास्तविक समय ट्राइड चार्ट में, तप की अलग-अलग डिग्री के समान प्रभाव प्राप्त करने के कई तरीके हैं। उपयोग की गई तकनीक में, विहित दृष्टिकोण ज्यामिति की निकटता पर दृश्य-अंतरिक्ष डेटा का शोषण है - हम सामान्य के साथ कई कदम उठाते हैं और यह निर्धारित करते हैं कि कुछ भी कितना करीब है जो हमें अस्पष्ट कर सकता है। यह एक बल्कि अनचाही हैक है (जैसे, सामान्य रूप से, सब कुछ जो हम इस ग्रह पर करते हैं), लेकिन यह बहुत अच्छा दिखता है।
यहाँ कोड है:

 //    float occlusion(vec3 at, vec3 normal) { //  ,     float b = 0.; //    for (int i = 1; i <= 4; ++i) { //   .06 --     float L = .06 * float(i); float d = world(at + normal * L); //           b += max(0., L - d); } //   1    return min(b, 1.); }

एक साधारण छाया को और भी सरल बनाया जाता है - हम बीम को एक बिंदु से प्रकाश स्रोत में जाने देते हैं और देखते हैं कि क्या यह रास्ते में किसी चीज के खिलाफ आता है।

 if (trace(at, normalize(l_dir), EPSILON*2.) < length(l_dir)) return vec3(0.);

कृपया ध्यान दें कि आप उस बिंदु से शुरू नहीं कर सकते, आपको थोड़ा पीछे जाने की जरूरत है (होमवर्क: क्यों?)

और अंत में, हम वहां कोहरा डालते हैं ताकि परिवेश प्रकाश के साथ पृष्ठभूमि विलीन न हो:

 color = mix(color, vec3(0.), smoothstep(0.,20.,path));

कुल:

भौतिक मूल्य

लेकिन यह अभी भी ग्रे और नीरस है। चलो गेंद और विमान को अलग-अलग रंग बनाते हैं। और इसलिए कि गेंद में धातु पर प्रकाश डाला गया है।
आइए इसके लिए एक material_t संरचना बनाएं:

 struct material_t { vec3 diffuse; float specular; };

हम अपनी दुनिया को उन कार्यों में विभाजित करते हैं जो व्यक्तिगत सामग्रियों की ज्यामिति को वापस करते हैं, और निम्नलिखित फ़ंक्शन लिखते हैं:

 //      material_t wmaterial(vec3 a) { //     material_t m = material_t(vec3(.5, .56, 1.), 200.); float closest = s_ball(a); //     --  float sample = s_floor(a); //     if (sample < closest) { //    closest = sample; //    --    m.diffuse = vec3(1.-mod(floor(ax)+floor(az), 2.)); m.specular = 0.; } return m; }

अब यह सामग्री का उपयोग करने के लिए पर्याप्त है, और प्रकाश समारोह में रंग स्थिर नहीं है।
हाइलाइट्स को फाइनल टच में जोड़ें। सामान्य तौर पर, स्पेक्युलर चकाचौंध भी एक बैसाखी-बैसाखी है, धातुओं से प्रकाश प्रतिबिंब के वास्तविक प्रभाव को अनुकरण करने का प्रयास (यह करने के लिए शारीरिक रूप से ईमानदारी से कठिन है - यह सभी प्रकार के बीआरडीएफ, रेंडरिंग समीकरणों, मेट्रोपोलिस और अन्य भारी शैक्षणिक ग्राफिक्स के अनुसार बीमिंग से शुरू होता है जो मुझे समझ में नहीं आता है। ), इसलिए, इस आशय का अनुमान लगाने के लिए विभिन्न तरीकों का एक ढेर है। यहां हम सामान्यीकृत ब्लिन-फोंग विधि का उपयोग करते हैं, जो कि पर्यवेक्षक और प्रकाश स्रोत के बीच सामान्य और अर्ध-वेक्टर के बीच के कोण के कोसाइन को कम करता है। स्पेक्युलर चकाचौंध भौतिक रूप से सामग्री के फैलाने वाले रंग से स्वतंत्र है।
लंबा, छोटा, यहाँ कोड है:

 if (m.specular > 0.) { // , ,  --        vec3 h = normalize(normalize(l_dir) + normalize(eye-at)); //      color += l_color * pow(max(0.,dot(normal,h)), m.specular) * (m.specular + 8.) / 25.; }

कुल:

मटर की दीवार के बारे में कैसे

हमारी गेंद संदिग्ध रूप से कुछ भी प्रतिबिंबित नहीं करती है, आइए इसे प्रतिबंधित करें।
सामग्री में एक परावर्तन क्षेत्र जोड़ें, घटना प्रकाश का अंश निर्दिष्ट करें जो पर्यवेक्षक में परिलक्षित होगा।
आइए प्रतिबिंब प्रतिबिंब में ट्रेस लपेटें:

 //        vec3 result_color = vec3(0.); //    float k_reflectivity = 1.; for (int i = 0; i < MAX_REFLECTIONS; ++i) { //    float path = trace(O, D, 0.); //      ,  if (path < 0.) break; // ,    vec3 pos = O + D * path; vec3 nor = wnormal(pos); //     material_t mat = wmaterial(pos); //   vec3 color = .15 * (1. - occlusion(pos, nor)) * mat.diffuse; //    color += enlight(pos, nor, O, mat, vec3(1., 1.5, 2.), vec3(2.*cos(t), 2., 2.*sin(t))); color += enlight(pos, nor, O, mat, vec3(2., 1.5, 1.), vec3(2.*sin(t*.6), 3., 2.*cos(t*.6))); // -  color = mix(color, vec3(0.), smoothstep(0.,20.,path)); //      result_color += k_reflectivity * color; //     k_reflectivity *= mat.reflectivity; // ,      if (k_reflectivity < .1) break; //        D = normalize(reflect(D, nor)); O = pos + D * EPSILON*2.; }

हम दृश्य में सभी प्रकार के अतिरिक्त जोड़ देंगे, और यहाँ उल्लू कैसे बनाया जाए:

लेकिन यह सब बुरा है।
बुरा, बुरा, बुरा।
यह सब दूरी कार्यों के बिना खींचा जा सकता है, और यह तेजी से भी काम करेगा। इसलिए, चलो सब कुछ बाहर फेंक दें और स्क्रैच से ज्यामिति खींचना शुरू करें।

लेकिन पहले, विकार की दुनिया में एक छोटा सा विषयांतर।

अराजकता सिद्धांत

पूरी तरह से चिकनी गोले और विमान सभी अच्छे हैं, लेकिन बहुत सिंथेटिक हैं। वास्तविक दुनिया अनियमित, अपूर्ण और आम तौर पर गंदगी से बनी है। इसलिए, अपनी तस्वीर के साथ इसके करीब जाने के लिए, आपको अपने स्वाद के लिए इसमें एक चुटकी चाट मिलाना होगा।
जैसा कि होना चाहिए अच्छा शोर करने के लिए, हमें एक ऐसा कार्य करना होगा जो एक पैरामीटर लेता है और एक यादृच्छिक संख्या उत्पन्न करता है जो इस पैरामीटर पर निर्भर करता है। यही है, समान पैरामीटर मानों के लिए आउटपुट पर समान संख्या होनी चाहिए। जीएलएसएल मानक पुस्तकालय में ऐसे कार्यों शोर, शोर 2 आदि के संदर्भ होते हैं, लेकिन व्यवहार में वे किसी भी निर्माता द्वारा लागू नहीं होते हैं (होमवर्क: क्यों?), इसलिए उन्हें नवीनतम संस्करण में भी देखा गया था। इसलिए, हमें अपना खुद का शोर लिखना होगा।
पारंपरिक दृष्टिकोण यह है:

 float hash(float x) { return fract(sin(x)*48737.3213); }

जहां 48737.3213 सिर्फ एक यादृच्छिक संख्या है जिसे मैंने संख्यात्मक कीपैड पर एक बिल्ली के साथ आँख बंद करके टाइप किया है। इंटरनेट पर लोग एक निश्चित संख्या को कॉपी-पेस्ट करना पसंद करते हैं और इसे हर जगह अपने साथ खींचते हैं, लेकिन मैंने इसके लिए स्पष्टीकरण नहीं देखा है।
Vec2 से शोर इस तरह से प्राप्त किया जा सकता है:

 float hash(vec2 x) { return hash(dot(x,vec2(71.,313.))); }

जैसा कि नाम से ही पता चलता है, ये फ़ंक्शन इनपुट नंबर के हैश की तरह हैं, और इस संख्या में थोड़े से बदलाव के साथ, उनका मूल्य महत्वपूर्ण रूप से बदल जाता है। हमारे उद्देश्यों के लिए, हमारे पास एक फ़ंक्शन होना चाहिए जिसका मूल्य अधिक सुचारू रूप से बदलता है। ऐसे कार्यों का निर्माण करने के कई तरीके हैं जो हैश पर आधारित हो सकते हैं, जिनमें से मुख्य हैं पर्लिन शोर, मूल्य शोर, सिंपल शोर।

इस सीज़न में इंटरनेट पर, यह पेर्लिन के शोर के बारे में गलतियाँ करने के लिए फैशनेबल है और इसे शोर के कई सप्तक के अतिरिक्त मानते हैं। मल्टी-ऑक्टेव शोर, या भग्न शोर, एक पूरी तरह से अलग तकनीक है जो न केवल पेरलिन के शोर पर, बल्कि किसी अन्य पर भी आधारित हो सकती है। पेरलिन का शोर इस तथ्य पर आधारित है कि हम एक एन-डायमेंशनल ग्रिड लेते हैं और इसके नोड्स (= सामान्यीकृत यादृच्छिक वैक्टर) पर यादृच्छिक सामान्यीकृत ग्रेडिएंट की व्यवस्था करते हैं, जिसके बाद अंतरिक्ष में प्रत्येक बिंदु के लिए हम निर्धारित कर सकते हैं कि हम ग्रिड की किस मात्रा में हैं, स्केलर उत्पाद की गणना करें सभी नोड्स और एन-लीनरीली इन उत्पादों के बीच। रैखिक प्रक्षेप को अधिक जटिल एक के साथ प्रतिस्थापित किया जा सकता है, उदाहरण के लिए, परिणामस्वरूप शोर के दूसरे व्युत्पन्न को सुचारू बनाना, यदि आपको किसी कारण से इसकी आवश्यकता है। यह पेर्लिन का शोर है। यह भारी और शांत है। दो मिनट के इस शैक्षिक कार्यक्रम के बाद, आप अब हर किसी को हँसा सकते हैं और अपनी नाक उठा सकते हैं:

हम उनके अत्यधिक कम्प्यूटेशनल जटिलता के कारण यहां सिम्प्लेक्स और पेर्लिन शोर का उपयोग नहीं करेंगे। ब्रह्मांड को गुलाम बनाने के हमारे मामूली लक्ष्यों के लिए, मूल्य शोर पर्याप्त है - हम ग्रिड नोड्स में यादृच्छिक मान लेते हैं और उनके बीच अंतर करते हैं, जैसे:

 //  value noise float noise(vec2 x) { // F -    , f -   vec2 F = floor(x), f = fract(x); //   vec2 e = vec2(1.,0.); //  f *= f * (3. - 2. * f); //   return mix( mix(hash(F+e.yy), hash(F+e.xy), fx), mix(hash(F+e.yx), hash(F+e.xx), fx), fy); }

अब कुख्यात भग्न शोर कई सप्तक के सरल योग द्वारा प्राप्त किया जाता है:

 //   float fnoise(vec2 x) { //       x += vec2(10.); //   return .5 * noise(x) + .25 * noise(x*1.97) + .125 * noise(x*4.04) + .0625 * noise(x*8.17) ; }

कुल मिलाकर, हमें शोर का ऐसा दृश्य प्रतिनिधित्व प्राप्त है:

( गुप्त बोनस ट्रैक -2 )

सब कुछ नष्ट कर देना

यादृच्छिकता के इस स्रोत का उपयोग करना, आप कुछ भी कर सकते हैं जो आप चाहते हैं। उदाहरण के लिए, एक शहर को ड्रा करें।
मुख्य विचार: हम अंतरिक्ष को क्वार्टर-सेक्टरों में हरा देते हैं, और प्रत्येक सेक्टर के लिए, इसकी समन्वय संख्या का उपयोग करके, हम अराजकता से भवन मापदंडों - आयामों, संख्याओं की संख्या, प्रकार को निकाल देंगे।
उसी तरह, उदाहरण के लिए, खिड़कियों को हाइलाइट किया जा सकता है - ऊंचाइयों और स्थिति के आधार पर हम एक यादृच्छिक संख्या लेते हैं और इसके आधार पर हम तय करते हैं कि इस "विंडो" में प्रकाश चालू है या नहीं।
कैमरा स्थिति, तारों वाला आकाश - यह सब भी यादृच्छिक मूल्यों के साथ बॉक्स से बाहर हो जाता है।
सामान्य तौर पर, मैं वास्तव में इस अल्प पाठ को लिखने से थक गया हूं। सबसे अधिक संभावना यह है कि आप इसे पढ़कर थक गए हैं। तो चलिए जरा देखते हैं ????? लाभ और पहले से ही बिस्तर पर जाओ!

ध्यान दें, अपने वीडियो कार्ड पर स्लाइड शो:

निष्कर्ष

यह इस अर्थव्यवस्था को छोटा करने के लिए अभी भी बना हुआ है - कुछ टिप्पणियों को हटा दें, चर और कार्यों के नाम को छोटा कर दें, रिक्त स्थान, लाइन फ़ीड को हटा दें, जिस तरह से हमारा ढांचा दूसरे भाग से उम्मीद करता है (शेयर्डटो के बजाय हमारे चर डालें) और जारी किया जा सकता है। खैर, यह असंभव है, क्योंकि यह अभी भी खराब स्वाद को पूरा करता है और आपको एक डिजाइनर की आवश्यकता होती है जो हर समय प्रोग्रामर को हरा देगा।
सामान्य तौर पर, यह होमवर्क है - इस शेडर को चलाने के लिए और देखें कि इसके साथ कितने बाइट्स योगिनी हैं। मेरा प्रारंभिक अनुमान 2..2.5Kb है।

और आखिरी एक: एक अजीब संयोग से, मैं आज अचानक (सोम, 10/21/2013) एक ही चीज के बारे में एनएसयू (नोवोसिबिर्स्क स्टेट यूनिवर्सिटी) में शाम को 19:30 बजे सभागार में बात करूंगा। 223 नई खेल सुविधाएं । आप नहीं आ सकते क्योंकि आप पहले से ही सब कुछ जानते हैं, योग्य। ठीक है, अर्थात्, इसके विपरीत - आओ, हम बचाएंगे!

पिछली श्रृंखला में: सी प्रोग्रामिंग भाषा में संगीत का संश्लेषण।
निम्नलिखित श्रृंखला में: ओपनसीएल पर वास्तविक समय में बहुभुज ज्यामिति का निष्पक्ष पथ अनुरेखण, संभवतः।

लिनक्स के लिए 1k / 4k इंट्रो बनाना, भाग 4