
आज मैं आपके ध्यान में एक अच्छा एल्गोरिथ्म लाऊंगा, जो कि, अभी हाल ही में (11 साल पहले) का आविष्कार किया गया था, तीन-हजार साल के इतिहास के साथ गिनती डिवाइस को "प्रोटोटाइप" के रूप में परोसा गया।
लेखक
छँटाई 2002 में न्यूजीलैंड के ऑकलैंड विश्वविद्यालय के तीन गणितज्ञों द्वारा प्रस्तुत की गई थी: जोशुआ जे। अरुलानंदम,
क्रिश्चियन एस। कैलुडे और माइकल जे। वैज्ञानिकों की गतिविधि के क्षेत्र असतत गणित, संख्या सिद्धांत, क्वांटम कंप्यूटिंग, सूचना सिद्धांत, दहनशील एल्गोरिदम हैं।

मुझे नहीं पता कि उनमें से तीन मूल विचार के मालिक हैं। शायद कलुद, जो अन्य बातों के अलावा, कम्प्यूटेशनल गणित का इतिहास पढ़ाते हैं। हर कोई जानता है, यूरोप में खातों का पूर्वज
अबेकस है , जो बाबुल से मिस्र, वहां से ग्रीस, वहां से रोम, जहां से पूरे यूरोप में जाता था। एंटिक "कैलकुलेटर" के संचालन का रूप और सिद्धांत इस "सरल" छंटाई के व्यवहार की याद दिलाता है कि इसे कभी-कभी "अबेकस सॉर्ट" कहा जाता है।
एल्गोरिथ्म

मान लीजिए कि आप
प्राकृतिक संख्याओं के एक
सेट को क्रमबद्ध करना चाहते हैं। एक दूसरे के नीचे, प्रत्येक संख्या को गेंदों की इसी संख्या की
क्षैतिज पंक्ति के रूप में बाहर रखना। और अब गेंदों के इन सभी समूहों को क्षैतिज रूप से नहीं, बल्कि
लंबवत देखें । गेंदों को सभी तरह से नीचे धकेलें। फिर, क्षैतिज पर स्विच करें और प्रत्येक पंक्ति में मोतियों को गिनें। संख्याओं का एक प्रारंभिक सेट मिला, केवल आदेश दिया गया।
कार्यान्वयन
30+ प्रोग्रामिंग भाषाओं में
मनका प्रकार यहां पाया जा सकता
है । हालाँकि, सॉफ्टवेयर कार्यान्वयन के दृष्टिकोण से, एल्गोरिथ्म कहीं भी सरल दिखता है, यह एक बहुत ही गैर-तुच्छ प्रकार है।
पतित करने का मामला

यह एक
रिवर्स-ऑर्डर की गई सरणी है । गेंदों की अधिकतम संभव संख्या को उच्चतम बिंदुओं से गिरना होगा।
सीमित प्रयोज्यता
विधि मुख्य रूप से
प्राकृतिक संख्याओं पर लागू होती है।
आप पूर्णांक को सॉर्ट कर सकते हैं, लेकिन यह अधिक जटिल है - नकारात्मक संख्याओं को सकारात्मक से अलग से संसाधित करना होगा।
कुछ भी क्रमबद्ध और भिन्न संख्याओं को रोकता नहीं है, यदि आप उन्हें पूर्णांक में लाते हैं (उदाहरण के लिए, सब कुछ
10 k से गुणा करें, सॉर्ट करें, और फिर
10 k से विभाजित करें)।
ठीक है, निश्चित रूप से, यहां तक कि पंक्तियों को इस तरह से सॉर्ट किया जा सकता है, अगर उनमें से प्रत्येक को एक सकारात्मक पूर्णांक के रूप में दर्शाया गया हो। लेकिन क्यों?
समय की जटिलता
एल्गोरिथ्म पर विचार करने के लिए संदर्भ के आधार पर, उनमें से पहले से ही 4 छंटाई कर रहे हैं।

ओ (1)
सार मामला, एक वैक्यूम में गोलाकार
मनका । यदि हम कल्पना करते हैं कि सभी चलती गेंदों को एक साथ स्थानांतरित किया गया है और जगह में गिर गया है। यह इस छँटाई के लिए एक अवास्तविक जटिलता है - न तो एल्गोरिदम के सिद्धांत में, न ही व्यवहार में।
ओ (√n)
एक
भौतिक मॉडल के लिए एक अनुमान जहां मोती अच्छी तरह से तेल बुनाई सुइयों नीचे सरकना। मुक्त गिरने का समय अधिकतम ऊंचाई के वर्गमूल के आनुपातिक है, जो बदले में
n का एक बहु है।
ओ (एन)
बॉल्स जो अभी तक अपने स्थानों पर नहीं पहुंचे हैं, एक साथ एक स्थान को एक पुनरावृत्ति में नीचे ले जाते हैं। भौतिक उपकरणों के मामले में इस जटिलता के बारे में बात करना उचित है जो इस सॉर्टिंग विधि, एनालॉग या डिजिटल हार्डवेयर कार्यान्वयन को लागू करते हैं।

ओ (एस)
S , सरणी के तत्वों का योग है। प्रत्येक गेंद व्यक्तिगत रूप से चलती है, और एक ही समय में गेंदों के समूह को रोल नहीं करते हैं। प्रोग्रामिंग भाषाओं में कार्यान्वयन के लिए पर्याप्त जटिलता का आकलन।
स्मृति कठिनाई
वांछित होने के लिए कुछ छोड़ देता है।
बीड सॉर्ट अपव्यय के लिए रिकॉर्ड धारक है - अतिरिक्त मेमोरी की लागत सरणी को संग्रहीत करने की लागत की तुलना में कई गुना अधिक है और
हे ( औसत
2 ) ।
भौतिक विज्ञान
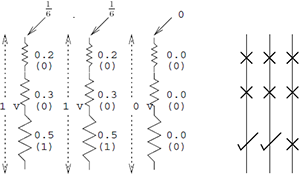
गेंदों की उपस्थिति या अनुपस्थिति को विद्युत प्रतिरोधों की एक श्रृंखला से गुजरने वाले
एनालॉग वोल्टेज के रूप में व्याख्या की जा सकती है। छड़ें जिसके साथ गेंदें चलती हैं,
विद्युत प्रतिरोधों के अनुरूप होती हैं, जिसमें वोल्टेज ऊपर से नीचे की ओर बढ़ता है।
इलेक्ट्रिकल इंजीनियरिंग की शर्तों के लिए इस्तेमाल होने वाली जीभ के लिए किक न करें, मेरे भौतिकी स्कूल में प्लस चार और माइनस के साथ ट्रिपल था।मैं इस
पीडीएफ-दस्तावेज़ में विवरण के लिए इलेक्ट्रोस्टैटिक्स के विशेषज्ञों को भेजता हूं।
वास्तव में
मनका प्रकार एक प्रकार की
गिनती है । प्रत्येक ऊर्ध्वाधर ट्रैक में गेंदों की संख्या ऊर्ध्वाधर के सीरियल नंबर की तुलना में बराबर या उससे अधिक सरणी में तत्वों की संख्या है।
एल्गोरिदम के लक्षण
| नाम | मनका प्रकार (मनका प्रकार); अबेकस प्रकार |
|---|
| लेखक | जोशुआ जे। अरुलानंदम, क्रिश्चियन एस। कैलुड, माइकल जे |
|---|
| प्रकाशन का वर्ष | 2002 |
|---|
| वर्ग | वितरण क्रमबद्ध करें |
|---|
| स्थिरता | नियमित |
|---|
| तुलना | कोई तुलना नहीं |
|---|
| समय की जटिलता | ओ (1) | ओ (√n) | ओ (एन) | ओ (एस) |
|---|
| स्मृति कठिनाई | ओ (एन 2 ) |
|---|
संदर्भ
ऑकलैंड विश्वविद्यालय की वेबसाइट पर बीएड छांटनाएल्गोरिथ्म पर लेखक के प्रलेखन, पीडीएफविभिन्न पीएल पर कार्यान्वयनअंग्रेजी विकिपीडिया पर मनका प्रकारलेखक होमपेज:
जोशुआ जे। अरुलानंदमक्रिश्चियन एस कैलुडमाइकल जे