☃️ 🔢 🚿 बंदरों और अनंत का कार्य 🙅 🧖 🤷

हर कोई जानता है कि यदि आप एक टाइपराइटर पर एक बंदर लगाते हैं और इसे हमेशा गलती से चाबियों पर खटखटाते हैं, तो, जल्दी या बाद में, यह युद्ध और शांति, पाइथागोरस के कार्यों का एक संग्रह और यहां तक कि उस लेख को भी प्रिंट करेगा।

एक आश्चर्यजनक तथ्य, लेकिन इससे भी अधिक दिलचस्प यह समझने की कोशिश करना है कि किसी विशिष्ट पाठ को टाइप करने में उसे कितना समय लगेगा। एक अतिरिक्त पैरामीटर को न चलाने के लिए - एक बंदर द्वारा टाइपिंग की गति - हम सवाल के जवाब की तलाश करेंगे: औसत पर कितने कीस्ट्रोक होंगे। क्या आपके लिए यह स्पष्ट है कि स्ट्रिंग "एबीसी" "आ" की तुलना में टाइप करना बहुत आसान है? यह पोस्ट इस समस्या को हल करने के लिए समर्पित है। साथ ही, फ़ंक्शन के उपसर्ग और इसके गुणों को समझाया गया है।

यह स्पष्ट है कि एक विशिष्ट पाठ लिखने पर एक बंदर द्वारा खर्च किया गया समय कुछ यादृच्छिक चर है। इसलिए, उसकी गणितीय अपेक्षा के बारे में पूछना तर्कसंगत है।

समस्या का औपचारिक विवरण

एक स्ट्रिंग एस को देखते हुए, राजधानी लैटिन अक्षरों ("ए" - "जेड") से मिलकर। एक चटाई खोजने की जरूरत है। यदि पूरे वर्ण समान रूप से टाइप किए गए हों ( 1/26 की प्रायिकता के साथ ) टाइप करने से पहले यादृच्छिक कीस्ट्रोक्स की संख्या की प्रतीक्षा की जाती है।

निर्णय कोड

यह समझने के लिए कि यह क्यों काम करता है और यह Pi () फ़ंक्शन क्या है, आपको पूरा लेख पढ़ने की आवश्यकता है :(

string s; //,    int n = s.length(); vector<int> p = Pi(s); vector<long double> pow(n+1); pow[0] = 1; int i; for (i = 1; i <= n; i++) { pow[i] = pow[i-1]*26; } long double ans = 0; for (i = n; i>0; i = p[i-1]) { ans += pow[i]; } cout << ans;

उपसर्ग समारोह

यह फ़ंक्शन हमें समस्या को हल करने में मदद करेगा। फ़ंक्शन उपसर्ग को डी। नॉट और एम। प्रैट (और डी। मॉरिस के समानांतर) द्वारा एक स्ट्रिंग ( केएमपी एल्गोरिदम) में प्रतिस्थापन खोजने के लिए पेश किया गया था। स्ट्रिंग s के लिए उपसर्ग फ़ंक्शन सबसे लंबे समय तक देशी स्ट्रिंग उपसर्ग की लंबाई लौटाता है, जो कि इसका प्रत्यय भी है।

उपसर्ग और प्रत्यय

यदि आप अंत से कुछ वर्णों को छोड़ देते हैं तो उपसर्ग लाइन की शुरुआत है। तो लाइन "अबा" में 4 उपसर्ग हैं: "" (खाली रेखा), "एक", "अब" और "अबा"। प्रत्यय समान है, लेकिन वर्ण शुरुआत से हटा दिए जाते हैं। हालाँकि, कुछ प्रत्यय और उपसर्ग मेल कर सकते हैं। स्ट्रिंग "अबा" के लिए 3 ऐसे उपसर्ग-प्रत्यय हैं: "", "एक" और "अबा" (चौथा प्रत्यय "बा" उपसर्ग "ab" से मेल नहीं खाता है)। एक प्रत्यय या उपसर्ग को उचित कहा जाता है यदि यह पूरी रेखा से छोटा है।

औपचारिक रूप से बोल: $\ pi (s) = अधिकतम \ {k \ ;; \ _, 0 \ le k & lt; | s |, \, pref_k (s) = suf_k (s) \}$

जहां pref _k (s) स्ट्रिंग s की लंबाई k का उपसर्ग है, और suf _k (s) स्ट्रिंग s की लंबाई k का प्रत्यय है।

दोनों ILC एल्गोरिथ्म और अन्य अनुप्रयोगों में, किसी दिए गए स्ट्रिंग के सभी उपसर्गों के लिए तुरंत उपसर्ग फ़ंक्शन पर विचार करना अधिक उपयोगी है। हां, यह डरावना लगता है - प्रत्येक उपसर्ग के लिए आपको सबसे बड़ा कस्टम उपसर्ग ढूंढना होगा जो प्रत्यय प्रत्यय से मेल खाता है। लेकिन वास्तव में, सब कुछ सरल है:

$\ pi_s (k) = \ pi (pref_k (s)), \, 1 \ le k \ le | s |$

इस तरह के एक विस्तारित उपसर्ग समारोह मुख्य रूप से उपयोगी है क्योंकि यह सरल की तुलना में गणना करना आसान है $\ _ पी$ । नीचे मान $\ pi_s ()$ for s = "अबाबाक"।

  k: 1 2 3 4 5 6
    s: अबाबाक
 पी (i): 0 0 1 2 3 0

गणना समारोह उपसर्ग

गणना कोड

 vector<int> Pi(string s) { int n = s.length(); vector<int> p(n); p[0] = 0; for (int i = 1; i < n; i++) { int j = p[i-1]; while (j > 0 && s[i] != s[j]) { j = p[j]; } if (s[i] == s[j]) j++; p[i] = j; } return p; }

एक त्वरित, ओ (एन) , फ़ंक्शन उपसर्ग की गणना दो सरल टिप्पणियों पर आधारित है।

(1) स्थिति k के लिए उपसर्ग-प्रत्यय प्राप्त करने के लिए , आपको स्थिति k-1 के लिए किसी प्रकार के उपसर्ग-प्रत्यय को लेने की जरूरत है और स्थिति k पर प्रतीक के अंत में इसे जोड़ना होगा।

(2) लंबाई n के स्ट्रिंग s के सभी प्रत्यय उपसर्ग के रूप में प्राप्त किए जा सकते हैं $\ pi_s (n), \, \ pi_s (\ pi_s (n)), \, \ pi_s (\ pi_s (\ pi_s (n)))$ और इसी तरह, जब तक कि अगला मूल्य 0. नहीं हो जाता। इस संपत्ति को "अबकाबा" लाइन पर चेक किया जा सकता है। यहां $\ pi_s (7) = 3, \, \ pi_s (3) = 1, \, \ pi_s (1) = 0$ , जो सभी उपसर्गों-प्रत्ययों ("अबा", "ए" और "") से मेल खाती है। ऐसा इसलिए है क्योंकि अधिकतम उपसर्ग प्रत्यय की लंबाई है $\ pi_s (n)$ । अगला उपसर्ग प्रत्यय छोटा होगा। लेकिन चूँकि पहली उपसर्ग-प्रत्यय शुरुआत और पंक्ति s के अंत में पाया जाता है, इसलिए अगला उपसर्ग-प्रत्यय पहले उपसर्ग-प्रत्यय में सबसे लंबा उपसर्ग-प्रत्यय होगा।

इसलिए, स्थिति i के लिए एक फ़ंक्शन उपसर्ग का निर्माण करने के लिए , यह पिछली स्थिति में फ़ंक्शन उपसर्ग के मान से पुनरावृत्ति करने के लिए पर्याप्त होता है जब तक कि प्रत्यय नए चरित्र के साथ जारी रहता है और यह भी एक उपसर्ग होगा (इसके लिए आपको केवल एक नए वर्ण की जांच करने की आवश्यकता है)। इस तरह के एक एल्गोरिथ्म को रैखिक समय में निष्पादित किया जाता है, क्योंकि प्रत्येक बार फ़ंक्शन के उपसर्ग का मान अधिकतम 1 से बढ़ जाता है, इसलिए, यह n समय से अधिक नहीं घट सकता है, जिसका अर्थ है कि नेस्टेड लूप n समय से अधिक नहीं में निष्पादित होगा।

KMP राज्य मशीन

समस्या को हल करने के लिए आवश्यक अगली गणितीय वस्तु एक परिमित अवस्था मशीन है जो किसी दिए गए स्ट्रिंग s में समाप्त होने वाली रेखाओं को स्वीकार करती है। यह ऑटोमेटन नथ-मोरिस-प्रैट एल्गोरिथ्म के एक और कम प्रसिद्ध संशोधन में उपयोग किया जाता है। एल्गोरिथ्म के इस संस्करण में, एक राज्य मशीन का निर्माण किया जाता है जो सभी लाइनों को स्वीकार करता है जो किसी दिए गए लाइन (टेम्पलेट) पर समाप्त होते हैं। फिर टेक्स्ट स्ट्रिंग को मशीन में प्रेषित किया जाता है। हर बार जब मशीन उस पर दिए गए पाठ को स्वीकार करती है, तो टेम्पलेट की अगली घटना का पता चलता है। यह मशीन है जो टाइपराइटर के पीछे एक बंदर की समस्या को हल करने में हमारी मदद करेगी।

एक राज्य मशीन क्या है

एक राज्य मशीन एक गणितीय वस्तु है जो किसी ऐसे बॉक्स के रूप में कल्पना करना सबसे आसान है जिसमें कुछ प्रकार की आंतरिक स्थिति है। प्रारंभ में, बॉक्स प्रारंभिक स्थिति में है । आप बॉक्स में लाइनों को दर्ज कर सकते हैं, एक बार में एक वर्ण। प्रत्येक प्रतीक के बाद, बॉक्स वर्तमान स्थिति और दर्ज किए गए प्रतीक के आधार पर, अपनी स्थिति बदलता है। साथ ही, कुछ राज्य अच्छे हैं (गणितीय शब्द अंतिम अवस्था है )। वे कहते हैं कि एक ऑटोमेटन एक स्ट्रिंग को स्वीकार करता है यदि, उसे इस स्ट्रिंग चरित्र-दर-चरित्र को खिलाने के बाद, मशीन अच्छी स्थिति में है।

अंतरिक्ष यान को निर्धारित करने के लिए, प्रारंभिक अवस्था, अच्छे राज्यों और संक्रमण फ़ंक्शन को निर्धारित करना आवश्यक है - प्रत्येक राज्य और प्रतीक के लिए, आपको एक नया राज्य निर्दिष्ट करने की आवश्यकता है जिसमें ऑटोमेटन जाएगा। एक ऑटोमेटन को एक पूर्ण उन्मुख ग्राफ के रूप में खींचना सुविधाजनक है, जहां कोने स्थित हैं, और प्रत्येक किनारे पर एक प्रतीक लिखा है। प्रत्येक शीर्ष पर प्रत्येक प्रतीक के साथ ठीक एक किनारे होना चाहिए। फिर, एक पंक्ति को संसाधित करने के लिए, आपको इस पंक्ति के पात्रों के साथ किनारों पर जाने की आवश्यकता है। यदि पथ अंतिम स्थिति में समाप्त हो जाता है, तो मशीन इस तरह की स्ट्रिंग लेती है।

इस ऑटोमेटन के निर्माण के लिए, हम उपसर्ग फ़ंक्शन का उपयोग करेंगे जो हम पहले से जानते हैं।
मशीन में n + 1 राज्य होंगे, जिनकी संख्या 0 से n तक होगी । स्टेट k लंबाई k के पैटर्न के उपसर्ग के साथ अंतिम k टाइप किए गए वर्णों के संयोग से मेल खाती है (यदि हम स्ट्रिंग "abac" की तलाश करते हैं, तो हम वर्तमान पाठ में रुचि रखते हैं: अंत में "abac", "aba", "ab", "a") यह एक वर्ण जोड़ने के बाद समान पाने के लिए पर्याप्त है)। राज्य 0 प्रारंभिक और राज्य n अंतिम होगा। कभी-कभी भ्रम हो सकता है: उदाहरण के लिए, "ababccc" शब्दों के लिए जब लाइन "zzzabab" को स्वचालित रूप से खिलाया जाता है, तो आप दोनों राज्य 2 और 4 का चयन कर सकते हैं। लेकिन, टाइप किए गए पाठ के बारे में आवश्यक जानकारी न खोने के लिए, हम हमेशा उच्चतम स्थिति का चयन करेंगे।

KMP राज्य मशीन उदाहरण

यहाँ स्ट्रिंग "अबाबाक" के लिए मशीन है। उदाहरण के लिए, वर्णमाला में केवल 'a' - 'c' अक्षर होते हैं। स्पष्टता के लिए संयुक्त समानांतर पसलियां। वास्तव में, केवल एक चरित्र प्रत्येक किनारे से मेल खाता है। प्रारंभिक स्थिति 0 है , अंतिम स्थिति 6 है ।

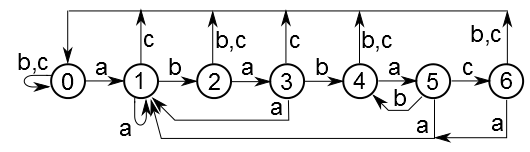
यह सुनिश्चित करना आसान है कि राज्य 0 से राज्य 6 तक का कोई भी मार्ग, चाहे वह कितना भी कठिन क्यों न हो, स्ट्रिंग "अबेक" के साथ समाप्त होना चाहिए। इसके विपरीत, कोई भी ऐसा रास्ता अनिवार्य रूप से राज्य 6 में समाप्त हो जाएगा।

राज्य मशीन निर्माण कोड

 string s; // . int n = s.length(); vector< vector<int> > nxt(n+1, vector<int>(256)); //   nxt[][] ==   vector<int> p = Pi(s); //  . .   nxt[0][s[0]] = 1; //    0   0. for (int i = 1; i <= n; i++) { for (int c = 0; c < 256; c++) nxt[i][c] = nxt[p[i-1]][c]; //p[]   ,   -1 if (i < n) nxt[i][s[i]] = i+1; }

ध्यान दें कि संक्रमण कैसे बने हैं। राज्य i से संक्रमणों की गणना करने के लिए , हम 2 विकल्पों पर विचार करते हैं। यदि नया वर्ण s [i] है, तो संक्रमण राज्य i + 1 में होगा । यहां सब कुछ स्पष्ट है: अगर आई पात्रों में एक मैच था, तो स्ट्रिंग के अगले चरित्र को जोड़ने से हम मैच की लंबाई 1 से बढ़ा देंगे। यदि प्रतीक मेल नहीं खाता है, तो हम बस राज्य से बदलाव की नकल करते हैं $\ pi_s (i)$ । क्यों? इस मामले में संक्रमण ठीक ≤i संख्या के साथ राज्य में होगा। इसलिए संक्रमण के बाद, हम टाइप किए गए पाठ के बारे में कुछ जानकारी भूल जाएंगे। आगे बढ़ने से पहले आप ऐसा कर सकते हैं। बहुत कम से कम जिसे हम मिटा सकते हैं, वह यह दिखावा करना है कि वास्तव में अब राज्य मैं नहीं, बल्कि है $\ pi_s (i)$ । ऊपर के उदाहरण में यह पसंद है, यह माना जा सकता है कि पाठ "abab" या "ab" के साथ समाप्त होता है। यदि "अबाब" से कोई संक्रमण नहीं है, तो आप "अब" से संक्रमण का उपयोग कर सकते हैं।

निर्णय

अब हम कार्य को हल करने के लिए तैयार हैं।
हम स्ट्रिंग एस के लिए एक केएमपी ऑटोमेटन का निर्माण करते हैं। चूंकि सभी वर्णों को एक बंदर द्वारा यादृच्छिक रूप से टाइप किया जाता है, इसलिए प्रतीक स्वयं हमारे लिए महत्वपूर्ण नहीं हैं, लेकिन केवल ट्रांज़िशन ग्राफ़ में किनारों। समस्या का सुधार इस प्रकार किया जा सकता है: चटाई को खोजें। राज्य 0 से एक यादृच्छिक चलने में संक्रमणों की संख्या की प्रतीक्षा कर रहा है जब तक कि राज्य n तक नहीं पहुंच जाता।

इस सूत्रीकरण में चर पेश करना तर्कसंगत है: ई _के , 0≤≤ --n - राज्य n तक पहुंचने तक संक्रमण की संख्या की अपेक्षा। E ₀ मूल समस्या का उत्तर होगा। Z को वैध वर्णों (वर्णमाला) का समुच्चय माना जाता है। आप समीकरणों की एक प्रणाली बना सकते हैं:

$E_n = 0$

$E_k = 1 + \ frac {1} {| Z |} \ sum_ {c \ _ Z} {E_ {nxt [k] [c]}}, k = 0..n-1$

समीकरण (1) का अर्थ है कि राज्य n पर पहुंचने पर , यादृच्छिक चलना बंद हो जाता है।
किसी भी अन्य राज्य के लिए, कुछ संक्रमण किया जाएगा, इसलिए, 1 शब्द समीकरण (2) में मौजूद है। दूसरा शब्द इन विकल्पों की संभावना से गुणा किए गए सभी संभावित विकल्पों का योग है। सभी संभावनाएं समान हैं - इसलिए, यह राशि के संकेत के रूप में निकाला जाता है।

ओ (एन ^ 3) में समस्या का एक समाधान पहले से ही है: रैखिक समीकरणों की निर्मित प्रणाली को गॉस विधि द्वारा हल किया जा सकता है। लेकिन अगर आप इस प्रणाली को थोड़ा देखते हैं और याद रखते हैं कि एक फ़ंक्शन उपसर्ग है, यानी समाधान बहुत सरल और तेज है।

एक परिमित राज्य मशीन के निर्माण को याद करें। (इसके बजाय, सादगी के लिए $\ pi_s$ मैं अभी उपयोग करूंगा $\ _ पी$ )। राज्य k से संक्रमण राज्य से संक्रमण के साथ लगभग मेल खाते हैं $\ pi (के)$ । संक्रमण में अंतर केवल प्रतीक s [k-1] के लिए है। इसलिए, राज्यों के कश्मीर के लिए समीकरणों के दाहिने हाथ (2) और $\ pi (के)$ केवल एक पद में भिन्नता है। के लिए समीकरण में $\ pi (के)$ लायक है $E_ {nxt [\ pi (k)] [s [k-1]]}$ के बजाय $E_ {nxt [k] [s [k-1]]}$ कश्मीर के लिए समीकरण में। इसके अलावा, nxt [k] [s [k-१]] = k + १ । इस तथ्य का उपयोग करते हुए, हम समीकरणों को फिर से लिख सकते हैं (2):

$E_k = E _ {\ _ pi (k)} + \ frac {1} {| Z |} (E_ {k + 1} -E_ {nxt [\ pi (k)] [s [k-1]]}}$

अब हमें एक और अवलोकन करने की जरूरत है। यह पता चला है

$nxt [\ pi (k) [s [k-1]] = \ pi (k + १)$

यानी किसी राज्य के लिए फ़ंक्शन उपसर्ग खोजने के लिए, आपको पिछले राज्य से फ़ंक्शन उपसर्ग लेने और अगले राज्य में जाने वाले प्रतीक द्वारा वहां से जाने की आवश्यकता है।
दरअसल, अगर हम राज्य पर विचार करते हैं $\ pi (के)$ , तो यह चरित्र के साथ समाप्त होने वाली रेखा से मेल खाती है [के -1]। तो इस प्रतीक पर संक्रमण हैं। उस सबसे बड़े राज्य पर विचार करें जहां से ऐसा संक्रमण मौजूद है, लेकिन जिसकी संख्या <k है । यदि प्रतीक s [k-1] का अनुसरण करने के बाद हमें किसी प्रकार का प्रत्यय मिलता है $pref_k (s)$ तब संक्रमण से पहले यह एक प्रत्यय था $pref_ {k-1} (s)$ । चूंकि यह सबसे सही राज्य था, यह अधिकतम उपसर्ग-प्रत्यय से मेल खाता है $pref_ {k-1} (s)$ , जिसका मतलब है कि इसकी एक संख्या है $\ pi (k-1)$ । इसलिए हमें यह अद्भुत और उपयोगी तथ्य मिला।

तब (3) में परिवर्तित किया जाता है:

$E_k = E _ {\ pi (k)} + \ frac {1} {| Z |} (E_ {k + 1} -E _ {\ pi (k + 1)})$

या दूसरे तरीके से:

$| जेड | (E_k - E _ {\ pi (k)}) = (E_ {k + 1} -E _ {\ pi (k + 1)})$

समान चिह्न के दोनों किनारों पर नकारात्मक संख्याएं हैं (यह तर्कसंगत है कि अधिक कश्मीर , कम ई _के )। दोनों पक्षों को -1 से गुणा करें।

$| जेड | (E _ {\ pi (k)} - E_k) = E _ {\ pi (k + 1)} - E_ {k + 1}$

लेकिन (4) केवल k> 0 के लिए मान्य है। K = 0 के लिए, हम स्पष्ट रूप से समीकरण (2) लिख सकते हैं, क्योंकि केवल Z | संक्रमण 1 राज्य की ओर जाता है, और बाकी सभी राज्य 0 पर वापस आते हैं:

$E_0 = 1 + \ frac {1} {| Z |} E_1 + \ frac {| Z- -1 -1 {{| Z |} E_0$

अब हम बाईं ओर के सभी चर इकट्ठा करते हैं, समीकरण को गुणा करें | Z | और प्रतिस्थापित करें $0 = \ pi (1)$ (एक वर्ण के लिए उपसर्ग फ़ंक्शन हमेशा 0 होता है, क्योंकि एक वर्ण में गैर-रिक्त उपसर्ग नहीं होते हैं)

$E _ {\ pi (1)} - E_1 = | Z |$

मैं अपने आप को समीकरणों को दोहराने की अनुमति देता हूं (1), (4) और (5), क्योंकि वे सिस्टम बनाते हैं जिसे हम अब विश्लेषणात्मक रूप से देखेंगे:

$E _ {\ pi (1)} - E_1 = | Z | \\ | जेड | (E _ {\ pi (k)} - E_k) = E _ {\ _ pi (k + 1)} - E_ {k + 1}, \, k = 1..n-1 \\ E_n = 0$

के = 1 पर दूसरे के बाईं ओर पहले समीकरण को प्रतिस्थापित करना, फिर k = 2 , आदि पर। हमें मिलता है:

$E _ {\ _ pi (k)} - E_k = | Z | ^ k, \, k = 1..n$

अब समाधान लगभग तैयार है: अब हम k ( n ) के लिए (6) पर विचार करते हैं और याद करते हैं $E_n = 0$ हमें मिलता है:

$E _ {\ _ pi (n)} = | Z | ^ n$

हम इस मान को (6) में प्रतिस्थापित करते हैं $k = \ pi (n)$ - हमें मिलता है:

$E _ {\ pi (\ pi (n))} = | Z | ^ n + | Z | ^ {\ pi (n)}$

इसी तरह, हम प्राप्त करते हैं:

$E _ {\ pi (\ pi (\ pi (n)))} = | Z | ^ n | Z | ^ {\ pi (n)} + | Z | ^ {\ pi (\ pi (n))} |$

और इसलिए हम तब तक जारी रख सकते हैं जब तक हम एक अभिव्यक्ति प्राप्त नहीं करते $E_0$ , जो संयोगवश, समस्या का उत्तर है। हम निरूपित करते हैं $\ pi ^ के$ फ़ंक्शन पंक्ति में k समय को लागू करता है $\ _ पी$ तब:

$E_0 = \ sum_ {k: \ pi ^ k (n) & gt; 0} | Z | ^ k$

इस प्रकार, हमने O (n) में समस्या का समाधान प्राप्त किया: स्ट्रिंग s के लिए फ़ंक्शन का एक उपसर्ग बनाएँ और उस पर से पुनरावृति करें n से शुरू होने तक हम 0 तक पहुंचते हैं, साथ ही साथ डिग्री जोड़ते हैं Z | उपसर्ग की वर्तमान लंबाई के बराबर। यह लेख की शुरुआत में दिया गया बहुत ही समाधान है।

(*) को देखते हुए यह स्पष्ट हो जाता है कि "एएए" टाइप करने के लिए स्ट्रिंग "आआ" अधिक कठिन क्यों है, क्योंकि "आआ" में केवल तीसरा पुनरावृत्ति $\ _ पी$ शून्य है, और दूसरी पंक्ति में आम तौर पर प्रत्ययों के बराबर कोई गैर-खाली उपसर्ग नहीं है और $\ _ पी$ तुरंत शून्य देता है।

टिप्पणी

उपसर्ग समारोह और ILC मशीन तार के साथ काम करने के लिए बहुत उपयोगी उपकरण हैं। अगर प्रिय पाठकों में रुचि है, तो मैं अन्य समस्याओं का समाधान कर सकता हूं। कृपया मुझे पीएम में किसी भी टाइपोस की जानकारी दें, धन्यवाद।

अपडेट:

सबसे पहले, Habré ( https://habrahabr.ru/post/264709/ ) पर सूत्रों के साथ एक लेख तैयार करने के लिए इसकी अद्भुत सेवा के लिए बहुत बहुत धन्यवाद। उसके बिना, यह लेख नहीं होता। यह शर्म की बात है कि मैं इसके बारे में तुरंत लिखना भूल गया।

दूसरे, कई टिप्पणीकार अपने अंतर्ज्ञान से भ्रमित होते हैं। प्रमेय में, यह अक्सर होता है। हां, पहली बार एक ही लंबाई के टाइपिंग की संभावनाएं समान हैं। हां, एक ही लंबाई के ग्रंथों की घटना की आवृत्ति एक अंतहीन यादृच्छिक पाठ में समान है। यह सब सच है, लेकिन यह इन तथ्यों से नहीं निकलता है कि लाइनों की पहली घटना से पहले वर्णों की संख्या की अपेक्षा समान होगी। और इसके विपरीत, इस तथ्य से कि अंतहीन पाठ में "hh" लाइन "hk" की तुलना में बाद में प्रकट होती है, यह इस बात का पालन नहीं करता है कि कैसीनो को काले के बाद लाल रंग में डाला जाना चाहिए।

चलो दो पंक्तियों "hh" और "hk" दिखाई देने तक उंगलियों पर अपेक्षा को गिनें। उम्मीद सभी से अधिक राशि है: पहली बार i अक्षर के लिए स्ट्रिंग टाइप करने की संभावना। बोल्ड में वाक्यांश का अर्थ है कि, पहले, टाइप किए गए अंतिम अक्षर खोज से मेल खाते हैं (यह संभावना दोनों पंक्तियों के लिए समान है), और दूसरी बात, खोज स्ट्रिंग पहले i-2 वर्णों के बीच नहीं होती है । यह दूसरा कारक भी अलग-अलग लाइनों के लिए भिन्न होता है। एक रेखा नहीं मिलने की संभावना बस सभी ग्रंथों की संख्या है जिसमें यह रेखा नहीं है, इस लंबाई के सभी ग्रंथों की संख्या से विभाजित है।

अब यह महत्वपूर्ण है: लंबाई k की पंक्तियों में "hk" कुल k + 1 : "k ... kh", "k ... kch", "k ... kchch", "k ... kchchch", ... "kch ... h" और "शामिल नहीं हैं। ज ... ज। " ऐसा इसलिए है क्योंकि प्रतीक "h" के बाद केवल "h" हो सकता है।

लम्बाई k की ड्रेन जिसमें "hh" नहीं है वह बहुत बड़ा होगा, अर्थात् F _{k + 1} - संख्या k + 1 के तहत फाइबोनैचि संख्या (ये संख्या 1, 1, 2, 3, 5, 8, 13, ... - प्रत्येक निम्नलिखित है) पिछले दो का योग)। उदाहरण के लिए, k = 2 3 लाइनों के लिए "kk", "kch", "hk" होगा। ये संख्या बहुत तेज़ी से बढ़ती है और इसलिए स्ट्रिंग "केके" के लिए उम्मीद की चटाई के लिए सभी शर्तें अधिक हो जाएंगी, क्योंकि अधिक संभावना है।

कृपया ध्यान दें कि यह सब इस तथ्य के कारण है कि पाठ को कुछ ही क्लिकों में पहली बार छापने की संभावना पाठ की शुरुआत और मध्य में एक बार भी पाठ को न छापने की संभावना पर निर्भर करती है। यह संभावना उन पंक्तियों की संख्या के लिए सीधे आनुपातिक है जिनमें एक दी गई रेखा नहीं है, लेकिन यह विभिन्न टेम्पलेट्स के लिए अलग है।

एक बार फिर, यह वह नहीं है जो मैं लेकर आया हूं, यह एक सर्वविदित तथ्य है, यद्यपि बहुत ही अनपेक्षित है। उदाहरण के लिए, इस लेख को देखें (ऐलिस और बॉब - 4 पैराग्राफ के बारे में एक कार्य के लिए देखें ): https://habrahabr.ru/post/279337/

बंदरों और अनंत का कार्य