👩🏻‍💻 🧒 👨‍🏭 सबसे छोटे के लिए मायने रखता है: दिज्कस्त्र या मैंने ट्विटर पर साक्षात्कार के लिए कैसे नहीं किया 👐🏻 🛳️ 💕

बहुत समय पहले मैं एक लेख के बारे में नहीं आया था कि कैसे माइकल कोज़कोव ट्विटर पर एक साक्षात्कार में एल्गोरिथम समस्या को हल नहीं कर सका। इस समस्या का समाधान लगभग अपने शुद्ध रूप में सबसे मानक ग्राफ एल्गोरिदम में से एक है, जिसका नाम है, दिज्क्स्ट्रा का एल्गोरिदम।
इस लेख में मैं इस समस्या को कुछ जटिल रूप में हल करने के उदाहरण पर दिक्क्स्ट्रा के एल्गोरिथ्म को बताने का प्रयास करूंगा। कोई भी, बिल्ली के नीचे, कृपया, रुचि रखता है।

पिछले चक्र लेख

पिछले लेखों में, एल्गोरिदम डीएफएस , बीएफएस और फोर्ड-बेलमैन पर विचार किया गया था।

समस्या का बयान

समस्या का विवरण फोर्ड-बेलमैन एल्गोरिथ्म द्वारा हल की गई समस्या के समान है: सभी अन्य के लिए भारित ग्राफ (प्रारंभिक) के चयनित शीर्ष से सबसे छोटा रास्ता खोजना आवश्यक है। अंतर केवल इतना है कि अब सभी किनारों का वजन गैर-नकारात्मक है।

एल्गोरिथम विवरण

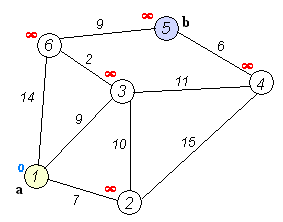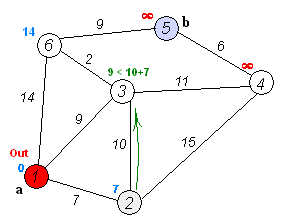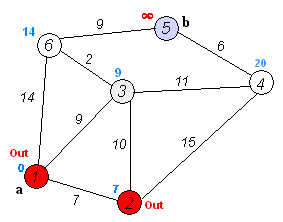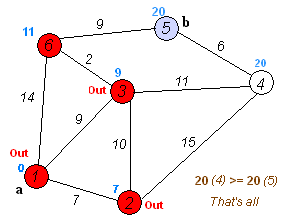
हम सभी छोरों को दो सेटों में विभाजित करते हैं: पहले से ही संसाधित और अभी तक नहीं। प्रारंभ में, सभी कोने असंसाधित होते हैं, और प्रारंभिक एक को छोड़कर सभी कोने की दूरी अनंत हैं, प्रारंभिक शीर्ष की दूरी 0 है।
प्रत्येक पुनरावृत्ति पर, असंसाधित कोने के सेट से, एक न्यूनतम दूरी के साथ एक शीर्ष लिया जाता है और संसाधित किया जाता है: इससे निकलने वाले सभी किनारों को आराम दिया जाता है, जिसके बाद शीर्ष को पहले से संसाधित किए गए शीर्षों के सेट में रखा जाता है।
मुझे याद है कि एज (यू, वी) की छूट, जैसा कि फोर्ड-बेलमैन एल्गोरिथ्म में है, डिस्ट [वी] = मिनट (डिस्ट [वी], डिस्ट [यू] + डब्ल्यू [यू, वी]), जहां डिस्ट को असाइन करने में समाहित है। v] प्रारंभिक वर्टेक्स से वर्टेक्स v की दूरी है, और w [u, v] u से v तक के किनारे का वजन है।

कार्यान्वयन

दिज्क्स्ट्रा के एल्गोरिथ्म के सरलतम कार्यान्वयन में, आपको न्यूनतम दूरी के साथ एक शीर्ष का चयन करने के लिए प्रत्येक पुनरावृत्ति की शुरुआत में सभी कोने से गुजरना होगा। यह काफी लंबा है, हालांकि इसे तंग रेखांकन में उचित ठहराया जा सकता है, इसलिए आमतौर पर कुछ डेटा संरचना का उपयोग दूरियों को दूर करने के लिए किया जाता है। मैं std :: set का उपयोग करूंगा, केवल इसलिए कि मुझे नहीं पता कि कैसे std में एक तत्व को बदलना है :: प्राथमिकता_करना =)
मैं यह भी मानता हूं कि ग्राफ को वेक्टर <वेक्टर <जोड़ी <int, int >>> किनारों के रूप में दर्शाया गया है, जहां किनारों [v] सभी किनारों का वेक्टर है, जो शीर्ष v से निकलता है, जिसमें किनारे का पहला क्षेत्र अंतिम शीर्ष और दूसरे की संख्या है वजन।

डिज्कस्ट्रा

void Dijkstra(int v) { //  int n = (int)edges.size(); dist.assign(n, INF); dist[v] = 0; set<pair<int, int> > q; for (int i = 0; i < n; ++i) { q.insert(make_pair(dist[i], i)); } //   -     while (!q.empty()) { //      pair<int, int> cur = *q.begin(); q.erase(q.begin()); //     for (int i = 0; i < (int)edges[cur.second].size(); ++i) { //   if (dist[edges[cur.second][i].first] > cur.first + edges[cur.second][i].second) { q.erase(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first)); dist[edges[cur.second][i].first] = cur.first + edges[cur.second][i].second; q.insert(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first)); } } } }

शुद्धता का प्रमाण

मान लीजिए कि एक एल्गोरिथ्म को वर्टेक्स यू से एक ग्राफ पर चलाया गया था और कुछ कोने के लिए एक गलत दूरी मान लौटाया गया था, और v इनमें से पहला वर्जन है (जिस क्रम में एल्गोरिथ्म कोने से बाहर निकलता है उस क्रम में पहली बार)। आइए उसके पूर्वज को यू से v तक के सबसे छोटे मार्ग में रखें।
ध्यान दें कि w की दूरी की गणना सही ढंग से धारणा द्वारा की जाती है

एल्गोरिथ्म डिस्ट '[w] <dist [v] द्वारा पाया जाता है। तब हम किनारे के अंतिम विश्राम को v: (s, v) मानते हैं। S की दूरी की सही गणना की गई थी, जिसका अर्थ है कि यू से लेकर वी डिस्टेंस [s] + w [s, v] = dist '[v] <dist [v] तक एक पथ मौजूद है। संघर्ष
एल्गोरिथ्म डिस्ट '[w]> डिस्ट [वी] द्वारा पाया जाता है। तब हम वर्टेक्स डब्ल्यू के प्रसंस्करण के क्षण पर विचार करते हैं। इस क्षण में, किनारे (w, v) को आराम दिया गया था, और, तदनुसार, वर्टेक्स v की दूरी का वर्तमान अनुमान dist [v] के बराबर हो गया, और निम्नलिखित आराम के दौरान यह कम नहीं हो सका। संघर्ष

इस प्रकार, एल्गोरिथ्म सही ढंग से काम करता है।
ध्यान दें कि यदि ग्राफ़ में नकारात्मक भार के किनारे थे, तो वर्टेक्स डब्ल्यू को बाद में वर्टेक्स v से बाहर थूक दिया जा सकता है, क्रमशः, किनारे (w, v) को आराम नहीं दिया गया था। डीजकस्ट्रा का एल्गोरिथ्म केवल नकारात्मक वजन के किनारों के बिना रेखांकन के लिए काम करता है!

एल्गोरिथ्म की जटिलता

कोने को कुछ डेटा संरचना में संग्रहीत किया जाता है जो एक मनमाना तत्व को बदलने और न्यूनतम निकालने के संचालन का समर्थन करता है।
प्रत्येक शीर्ष को एक बार बिल्कुल निकाला जाता है, अर्थात, ओ (वी) अर्क की आवश्यकता होती है।
सबसे खराब स्थिति में, प्रत्येक किनारे संरचना के एक तत्व में परिवर्तन की ओर जाता है, अर्थात, ओ (ई) परिवर्तन।
यदि कोने एक सरल सरणी में संग्रहीत किए जाते हैं और रैखिक खोज एल्गोरिथ्म का उपयोग न्यूनतम खोजने के लिए किया जाता है, तो दिक्जस्ट्रा एल्गोरिथ्म की समय जटिलता हे (V * V + E) = O (V²) है।
यदि हम बाइनरी हीप (या सेट पर आधारित) के आधार पर कार्यान्वित प्राथमिकता कतार का उपयोग करते हैं, तो हमें ओ (वी लॉग वी + ई लॉग ई) = ओ (ई लॉग वी) मिलता है।
यदि प्राथमिकता पंक्ति को फिबोनाची ढेर के आधार पर लागू किया गया था, तो जटिलता ओ (वी लॉग वी + ई) का सबसे अच्छा अनुमान प्राप्त किया जाता है।

लेकिन ट्विटर पर इंटरव्यू लेने का क्या काम है इससे क्या लेना-देना है?

साक्षात्कार से कार्य स्वयं हल करना बहुत दिलचस्प नहीं है, इसलिए मैं इसे जटिल बनाने का सुझाव देता हूं। लेख को आगे पढ़ने से पहले, मैं सुझाव देता हूं कि आप मूल समस्या कथन से खुद को परिचित करें

साक्षात्कार से नया कार्य सेटिंग

हम कार्य को "एक आयामी" साक्षात्कार से बुलाएंगे। फिर k- आयामी एनालॉग में k संख्याओं के आधार पर कॉलम होंगे, जिनमें से प्रत्येक के लिए ऊंचाई ज्ञात है। पानी एक स्तंभ से निचली ऊँचाई के किनारे के किनारे या किनारे से निकल सकता है।
"आसन्न पोस्ट" क्या हैं? प्रत्येक कॉलम में पड़ोसियों की अपनी सूची है, जो भी हो। यह पूरे नक्शे के माध्यम से एक पाइप से दूसरे कॉलम से जुड़ा जा सकता है, या "सहज रूप से आसन्न" बाड़ द्वारा बंद किया जा सकता है
जमीन क्या है? प्रत्येक कॉलम के लिए, हम एक अलग फ़ील्ड सेट करेंगे जो यह इंगित करेगा कि क्या यह चरम है। शायद हमारे पास खेत के बीच में एक छेद है?

अब हम इस समस्या को हल करेंगे, और समाधान की जटिलता ओ होगी (एन लॉग एन)

हम इस समस्या में ग्राफ का निर्माण इस प्रकार करते हैं:

कोने स्तंभ होंगे (और "किनारे से परे" स्थित एक और डमी वर्टेक्स)।
दो कोने एक किनारे से जुड़े होंगे यदि हमारी प्रणाली में वे आसन्न हैं (या यदि इनमें से एक कोने "बढ़त" है, तो दूसरा चरम स्तंभ है)
पसली का वजन दो स्तंभों की ऊँचाई के बराबर होगा जो इसे जोड़ता है

इस तरह के "पेचीदा" ग्राफ पर भी, दिज्क्स्ट्रा के एल्गोरिथ्म को चलाने से, हमें कुछ भी उपयोगी नहीं मिलता है, इसलिए हम "ग्राफ़ में पथ के वजन" की अवधारणा को संशोधित करते हैं - अब यह सभी किनारों के वजन का योग नहीं होगा, लेकिन उनकी अधिकतम। मैं आपको याद दिलाता हूं कि वर्टेक्स यू से वर्टेक्स वी तक की दूरी यू और वी को जोड़ने वाले सभी रास्तों के भार की न्यूनतम है।
अब सब कुछ जगह में गिरता है: एक निश्चित केंद्रीय स्तंभ से किनारे पर जाने के लिए, आपको कुछ पथ (जिसके साथ पानी निकल जाएगा) के साथ जाने की आवश्यकता है, और इस पथ के स्तंभों की अधिकतम स्थिति सबसे अच्छी स्थिति में "दूरी" के साथ मेल खाएगी। प्रारंभिक कॉलम से "एज" (या, चूंकि ग्राफ उन्मुख नहीं है, "किनारे" से प्रारंभिक कॉलम तक)। यह केवल दिक्जस्ट्रा एल्गोरिथ्म को लागू करने के लिए बनी हुई है।

कार्यान्वयन

 void Dijkstra(int v) { //  int n = (int)edges.size(); dist.assign(n, INF); dist[v] = 0; set<pair<int, int> > q; for (int i = 0; i > n; ++i) { q.insert(make_pair(dist[i], i)); } //   -     while (!q.empty()) { //      pair<int, int> cur = *q.begin(); q.erase(q.begin()); //     for (int i = 0; i < (int)edges[cur.second].size(); ++i) { //   if (dist[edges[cur.second][i].first] > max(cur.first, edges[cur.second][i].second)) { q.erase(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first)); dist[edges[cur.second][i].first] = max(cur.first, edges[cur.second][i].second); q.insert(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first)); } } } }

लेकिन यह मूल समाधान की तुलना में कठिन और लंबा है! इसकी जरूरत किसे है!

मैं इस तथ्य पर आपका ध्यान आकर्षित करता हूं कि हमने समस्या को सामान्य तरीके से हल किया है। यदि हम वास्तव में उस शब्दांकन पर विचार करते हैं जो साक्षात्कार में था, तो यह ध्यान देने योग्य है कि प्रत्येक पुनरावृत्ति में दो से अधिक असंसाधित कोने नहीं होते हैं, जिसकी दूरी अनंत के बराबर नहीं है, और आपको केवल उनमें से चुनने की आवश्यकता है।
यह नोटिस करना आसान है कि एल्गोरिथ्म मूल लेख में प्रस्तावित के साथ पूरी तरह से मेल खाता है।

क्या यह अच्छा काम था?

मुझे लगता है कि यह कार्य दीजकस्ट्रा के एल्गोरिदम को समझाने के लिए उपयुक्त है। यह देने लायक था या नहीं, इस बारे में मेरी व्यक्तिगत राय स्पॉइलर के नीचे छिपी हुई है। यदि आप इसे देखना नहीं चाहते हैं - तो न खोलें।

छिपा हुआ पाठ

यदि कोई व्यक्ति रेखांकन में थोड़ा भी पारंगत है, तो वह निश्चित रूप से दिज्क्स्ट्रा एल्गोरिथ्म जानता है - वह पहले और सबसे सरल में से एक है। यदि किसी व्यक्ति को दिजाकस्ट्रा के एल्गोरिथ्म का पता है, तो उसे इस समस्या को हल करने में पांच मिनट का समय लगेगा, जिनमें से दो की हालत पढ़ने और तीन कोड लिखने की है। बेशक, आपको डिजाइनर या सिस्टम प्रशासक की रिक्ति के लिए एक साक्षात्कार में ऐसा काम नहीं करना चाहिए, लेकिन यह देखते हुए कि ट्विटर एक सामाजिक नेटवर्क है (और ग्राफ़ पर समस्याओं को अच्छी तरह से हल कर सकता है), और आवेदक को डेवलपर की रिक्ति के लिए साक्षात्कार दिया गया था, मेरा मानना है कि एक गलत उत्तर के बाद यह कार्य वास्तव में विनम्रतापूर्वक अलविदा कहने लायक था।
हालांकि, यह कार्य साक्षात्कार में केवल एक ही नहीं हो सकता है: मेरी पत्नी, अर्थशास्त्र अकादमी के अर्थशास्त्र संकाय के एक 4 वर्षीय छात्र ने लगभग दस मिनट में हल किया, लेकिन वह शायद ही एक अच्छा प्रोग्रामर है =)
एक बार फिर से: कार्य स्मार्ट को बेवकूफ या ओलंपियाड से अलग नहीं करता है नवपल्लीनिंदिकी से। यह उन लोगों को अलग करता है जो कम से कम एक बार गिनती (+ जो भाग्यशाली हैं) के बारे में सुनते हैं, जिन्होंने नहीं सुना।
और, निश्चित रूप से, मेरा मानना है कि साक्षात्कारकर्ता को आवेदक का ध्यान कोड में त्रुटि की ओर मोड़ना चाहिए था।

पुनश्च

हाल ही में, मैंने एल्गोरिदम पर लेखों की एक छोटी श्रृंखला लिखी है। अगले लेख में, फ्लॉयड एल्गोरिथम पर विचार करने की योजना है, और फिर ग्राफ़ में पथ खोज एल्गोरिदम की एक छोटी सारांश तालिका दें।

सबसे छोटे के लिए मायने रखता है: दिज्कस्त्र या मैंने ट्विटर पर साक्षात्कार के लिए कैसे नहीं किया