उत्पादन कार्य - गोल यात्रा

“उत्पादन समारोह एक उपकरण है जो आंशिक रूप से एक बैग की याद दिलाता है। कई वस्तुओं को अलग-अलग ले जाने के बजाय, जो मुश्किल हो सकता है, हमने उन्हें एक साथ रखा, और फिर हमें केवल एक आइटम - एक बैग ले जाने की आवश्यकता है। "
डी। पोइया

परिचय

गणित को दो दुनियाओं में विभाजित किया गया है - असतत और निरंतर। वास्तविक दुनिया में इसके लिए और दूसरे के लिए एक जगह है, और अक्सर विभिन्न कोणों से एक घटना के अध्ययन के लिए दृष्टिकोण किया जा सकता है। इस लेख में, हम जनरेटिंग फ़ंक्शंस का उपयोग करके समस्याओं को हल करने के लिए एक विधि पर विचार करेंगे - एक पुल एक असतत दुनिया से निरंतर एक तक, और इसके विपरीत।

कार्यों को उत्पन्न करने का विचार काफी सरल है: हम एक अनुक्रम को जोड़ते हैं <g ₀ , g ₁ , g ₂ , ..., g _n > असतत वस्तु के साथ, एक शक्ति श्रृंखला g ₀ + g ₁ z + g ₂ z ² + ... + g _n z ⁿ + ... - ऑब्जेक्ट निरंतर है, जिससे हम समस्या के समाधान के लिए गणितीय विश्लेषण उपकरणों के एक पूरे शस्त्रागार को जोड़ते हैं। यह आमतौर पर कहा जाता है कि एक अनुक्रम उत्पन्न होता है, एक जनरेटिंग फ़ंक्शन द्वारा उत्पन्न होता है । यह समझना महत्वपूर्ण है कि यह एक प्रतीकात्मक निर्माण है, अर्थात, z प्रतीक के बजाय, कोई भी वस्तु हो सकती है जिसके लिए जोड़ और गुणन कार्यों को परिभाषित किया गया है।

निर्माण कार्यों का इतिहास

यह ज्ञात है कि अंग्रेजी गणितज्ञ अब्राहम डी मुवर ने कार्यों को उत्पन्न करने के तरीके की नींव रखी थी, और हम इस पद्धति के आगे के विकास और निरंतरता का श्रेय महान गणितज्ञ को देते हैं, जिसका नाम लियोनार्ड यूलर है।

18 वीं शताब्दी के 50 के दशक में यूलर ने निम्नलिखित समस्या का समाधान किया: 2 ⁰ , 2 ¹ , 2 ² , ..., 2 ⁿ ग्राम और कितने तरीकों से वजन का उपयोग करके वजन किया जा सकता है? इस समस्या को हल करने के लिए, उन्होंने कार्यों को उत्पन्न करने की तत्कालीन अज्ञात विधि का उपयोग किया, जिसे यह लेख समर्पित है। हम इस कार्य पर थोड़ी देर बाद लौटेंगे, क्योंकि हम जनरेटिंग फ़ंक्शन के उपकरण के साथ अधिक विस्तार से व्यवहार करेंगे।

कार्य उत्पन्न करने की विधि

हम इस शक्तिशाली तंत्र का अध्ययन शुरू करेंगे जो हमें एक सरल कार्य के साथ कई समस्याओं को हल करने की अनुमति देता है: आप एक पंक्ति में काले और सफेद गेंदों को कितने तरीकों से व्यवस्थित कर सकते हैं, जिनमें से कुल संख्या n है?

हम सफेद गेंद को प्रतीक ○, काले एक - ●, टी _n - गेंदों के स्थानों की वांछित संख्या से दर्शाते हैं। प्रतीक। - गेंदों की शून्य संख्या को दर्शाता है। एक संयोजन समस्या के समाधान की तरह, हम तुच्छ मामलों से शुरू करते हैं:

यदि n = 1, तो स्पष्ट रूप से 2 तरीके हैं - या तो सफेद गेंद लेने के लिए, या काली गेंद को ● लेने के लिए, इसलिए T ₂ = 2।

यदि n = 2, तो व्यवस्था करने के 4 तरीके हैं: then, ● ●, ● 2, ● अंक।

N = 3 के मामले पर विचार करें। हम एक सफेद गेंद के साथ शुरू कर सकते हैं और ऊपर वर्णित 4 संयोजनों के साथ जारी रख सकते हैं ○○, ○ ●, ○ ● ○, we ● अंक, या हम एक काले रंग की गेंद से शुरू कर सकते हैं और इसी तरह 4 गेंदों के साथ जारी रख सकते हैं ● ○○, ● white ●, ● अंक,, ● अंक।

नतीजतन, गेंदों की संख्या दोगुनी हो गई, अर्थात टी ₃ = ₂ टी ₂ । इसी तरह, टी ₄ = 2 टी ₃ , अर्थात्, सभी एन के लिए सामान्यीकरण, हम पुनरावृत्ति समीकरण टी _एन = 2 टी _{एन -1 प्राप्त करते हैं} जो इस समस्या का समाधान है। इस समीकरण के समाधान का अनुमान आसानी से लगाया जा सकता है - T _n = 2 ⁿ (2 n2 ^n-1 = 2 ^{n के बाद से} )।

लेकिन क्या होगा अगर हमारे पास खराब अनुमान है? और क्या होगा यदि समीकरण अधिक जटिल है? सामान्य तौर पर, सृजन कार्य कहां से आते हैं?

गेंदों की व्यवस्था के सभी संभावित संयोजनों को "सारांशित करें":

G = ○○ + ○ + ● + Ø + ● ● + ○ ● ● + अंक + Ø + ○ + ○ ● + ○○ ● ○ ● ○ + ● ● कनेक्शन + ● ○○ + ● ○ ● + ○ ● ○ + अंक ● ... ...

पहली नज़र में इस तरह के एक बेतुके की स्वीकार्यता का सवाल छोड़ दिया जाता है। हम गेंदों के अनुक्रम को जोड़ेंगे और गुणा करेंगे। इसके अलावा, सब कुछ स्पष्ट है, लेकिन गेंदों के एक क्रम को दूसरे से गुणा करने का क्या मतलब है? गुणा ip ● ● ○ से हमें ○ ● get के अलावा और कुछ नहीं मिलता है। हम नोट करते हैं, हालांकि, संख्याओं के उत्पाद के विपरीत गेंदों का उत्पाद, कम्यूटेटिव नहीं है, क्योंकि ○ ● ○ ● ⋅ that ● ● ○ that। ●। प्रतीक a - कार्य में एक गुणक इकाई की भूमिका निभाता है, अर्थात, ⋅ ○○ ○○ ● = ⋅ ● = Ø = ○○ ● और गेंदों के किसी भी क्रम के साथ शुरू होता है।

एक श्रृंखला जी के साथ जोड़तोड़ की एक श्रृंखला का प्रदर्शन, अर्थात्, बाईं सफेद और काली गेंदों को बाहर निकालना

जी = ○ + ○ + (Ø + ● + ● + ○ + ● ● + ● ○ + ● अंक + ...) + ● (Ø + ○ + ● + + ○○ + ○ ● + ○ + ● + ..) = Ø + ○ जी + ● जी

हम समीकरण G = Ø + the G + ● G प्राप्त करते हैं।

इस तथ्य के बावजूद कि गुणा गैर-कम्यूटेटिव है, और हम वास्तव में बाएं और दाएं विभाजन के बीच अंतर नहीं करते हैं, हम अभी भी इस समीकरण को "अपने स्वयं के जोखिम और जोखिम पर" हल करने की कोशिश करते हैं। हमें मिलता है



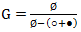
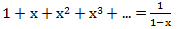
ज्यामितीय प्रगति के योग के सूत्र को देखते हुए , हमारे पास है

।

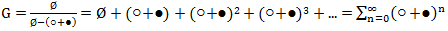
यह राशि बिलकुल एक बार संभव विभाजन के विकल्पों को भी ध्यान में रखती है। अगला, हम न्यूटन द्विपद सूत्र का उपयोग करते हैं: जहाँ N के k के संयोजन की संख्या है। फिर, इसे ध्यान में रखते हुए, हमारे पास:



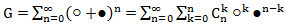
● ^k ● n k पर k के n के संयोजन की संख्या के बराबर गुणांक n गेंदों के क्रम में k के टुकड़ों और ● गेंदों की संख्या में n के टुकड़ों की संख्या के कुल दृश्यों को दर्शाता है। इस प्रकार, n गेंदों के स्थानों की कुल संख्या k के सभी संभावित मूल्यों पर योग है। जैसा कि ज्ञात है ।

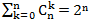
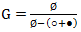
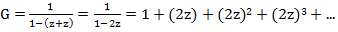
यह सूत्र सीधे प्राप्त किया जा सकता है by द्वारा 1, और ○ और ● z के द्वारा (उनकी समानता को देखते हुए) की जगह। हमें मिलता है यही है, z ⁿ पर गुणांक 2 ^{n है} ।

विधि चर्चा

तो विभिन्न समस्याओं को हल करने में इस पद्धति को क्या काम करने योग्य है?

समस्या को हल करने के लिए एल्गोरिथ्म का वर्णन लगभग इस प्रकार किया जा सकता है: हम कुछ अनंत योग मानते हैं, जो अंततः एक औपचारिक शक्ति श्रृंखला जी (z) = g ₀ + g ₁ z + g ₂ z ² + ... + g _n z ⁿ + ... और गुणांक का प्रतिनिधित्व करता है। जी _के (स्पष्ट रूप से निर्दिष्ट नहीं) - मूल समस्या को हल करने की कुंजी हैं। तथ्य यह है कि श्रृंखला औपचारिक है यह दर्शाता है कि z - सिर्फ एक प्रतीक है, अर्थात, इसके बजाय कोई भी वस्तु हो सकती है: एक संख्या, एक गेंद, एक डोमिनो हड्डी, आदि। विश्लेषण में बिजली श्रृंखला के विपरीत, औपचारिक बिजली श्रृंखला को संख्यात्मक मान नहीं दिए जाते हैं और तदनुसार, संख्यात्मक तर्कों के लिए ऐसी श्रृंखला के अभिसरण के बारे में बात करने का कोई मतलब नहीं है।

G (z) = g ₀ + g ₁ z + g ₂ z ² + ... + g _n z ⁿ + ... - को अनुक्रम के लिए जनरेटिंग फंक्शन कहा जाता है <g ₀ , g ₁ , g ₂ , ..., g _n >। ध्यान दें, हालांकि, कि G (z) एक फ़ंक्शन है, यह अभी भी एक औपचारिक संकेतन है, अर्थात, हम किसी भी मान z = z ₀ को z के साथ z = 0 को छोड़कर स्थानापन्न नहीं कर सकते, क्योंकि G (0) = g _{0 है} ।

फिर, अनंत योग जी (z) के साथ विभिन्न परिवर्तन करते हुए, हम इसे एक बंद (कॉम्पैक्ट) रूप में बदलते हैं। अर्थात्, जनरेटिंग फंक्शन में 2 अभ्यावेदन होते हैं: अनंत और बंद, और, एक नियम के रूप में, समस्या को हल करने के लिए, अनंत रूप को बंद करने के लिए परिवर्तित करना आवश्यक है, और फिर पावर श्रृंखला में बंद फॉर्म का विस्तार करना है, और इस तरह गुणांक जी के लिए मान प्राप्त करना है।

शुरुआत में सामने आए प्रश्न का उत्तर देते हुए, हम यह कह सकते हैं: इस पद्धति की सफलता एक उत्पन्न करने वाले कार्य को बंद रूप में लिखने की क्षमता से जुड़ी है। इसलिए, उदाहरण के लिए, अनुक्रम के लिए जनरेटिंग फंक्शन <1, 1, 1, ..., 1> अनंत रूप में 1 + x + x ² + x ³ + ..., और बंद के रूप में दर्शाया गया है। ।

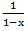
और अब, ज्ञान से लैस, आइए उस कार्य पर लौटते हैं जिसे ईयलर ने हल किया था।

तो, कार्य निम्नानुसार है: 2 ⁰ , 2 ¹ , 2 ² , ..., 2 ⁿ ग्राम और कितने तरीकों के वजन का उपयोग करके वजन किया जा सकता है?

मुझे नहीं पता कि इस समस्या के समाधान के लिए यूलर कब तक आया, लेकिन इसकी अप्रत्याशितता में हड़ताली है। खुद के लिए जज। यूलर उत्पाद को G (z) = (1 + z) (1 + z ² ) (1 + z ⁴ ) मानता है ... जो, कोष्ठक खोलने के बाद, अनंत श्रृंखला G (z) = 1 + g ₁ z + ₂ z ^{2 के} रूप में दर्शाया जाता है। + जी ₃ जेड ³ + ...।

गुणांक g _k क्या हैं? प्रत्येक g _k z ^{k के} लिए एक गुणांक है, और z ^k को कुछ मोनोमियल z ^2m के गुणनफल के रूप में प्राप्त किया जाता है, अर्थात g ^k , ^k की संख्या 1, 2, 2 ² के योग के रूप में k के विभिन्न अभ्यावेदन की संख्या है। २ ^३ , ..., २ ^मी , ...। दूसरे शब्दों में, जी _k दिए गए वज़न के साथ k ग्राम में भार को मापने के तरीकों की संख्या है। बस हम जिसे ढूंढ रहे थे!

यूलर का अगला कदम पिछले की तुलना में कम नहीं है। वह समीकरण के दोनों किनारों (1-z) से गुणा करता है।

(1-z) G (z) = (1-z) (1 + z) (1 + z ² ) (1 + z ⁴ ) (1 + z ⁸ ) ...
(1-z) G (z) = (1-z2) (1 + z ² ) (1 + z ⁴ ) (1 + z ⁸ ) ...
(1-z) G (z) = (1-z ⁴ ) (1 + z ⁴ ) (1 + z ⁸ ) ...
(1-जेड) जी (जेड) = 1


एक तरफ जी (z) = 1 + g ₁ z + g ₂ z ² + g ₃ z ³ + ... दूसरी ओर, हम बस मिल गए । अंतिम समानता एक ज्यामितीय प्रगति के योग के अलावा और कुछ नहीं है, जो इसके बराबर है । इन दो समानताओं की तुलना करते हुए, हम जी ₁ = जी ₂ = जी ₃ = ... = 1 प्राप्त करते हैं, अर्थात, k ग्राम में किसी भी भार को 1, 2, 4, 8, ... ग्राम, वजन के साथ अनोखे तरीके से तौला जा सकता है।

पुनरावृत्ति संबंधों को हल करना

सृजन संबंधी कार्य न केवल दहनशील समस्याओं को हल करने के लिए उपयुक्त हैं। यह पता चला है कि उनका उपयोग पुनरावृत्ति संबंधों को हल करने के लिए किया जा सकता है।

आइए फाइबोनैचि संख्याओं के परिचित अनुक्रम से शुरू करें। हम में से प्रत्येक इसके आवर्तक रूप को जानता है: F ₀ = 0, F ₁ = 1, F _n = F _n-1 + F _n-2 , n However 2. हालाँकि, सभी को इस सूत्र के रूप को बंद रूप में नहीं पता है और यह आश्चर्य की बात नहीं है, आखिरकार, इसकी संरचना में एक अपरिमेय संख्या ("सुनहरा अनुपात") शामिल है।

तो हमारे पास है

एफ ₀ = 0,
एफ ₁ = 1,
F _n = F _n-1 + F _n-2 , n _- 2

प्रत्येक पंक्ति को क्रमशः z ⁰ , z ¹ , ..., z ^{n से} गुणा करें:

z ⁰ ⋅ F ₀ = 0,
z ¹ ⋅ F ₁ = z,
z ^n- F _n = z ⁿ ⋅ F _n-1 + z _n- F _n-2 , n। 2

इन समानताओं को संक्षेप में लिखें: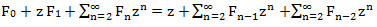



बाईं ओर निरूपित करें

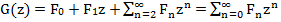
दाईं ओर के प्रत्येक शब्द पर विचार करें:



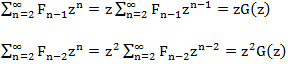
हमारे पास निम्नलिखित समीकरण G (z) = z + z G (z) + z ² G (z) हल है जो G (z) के संबंध में हम पाते हैं

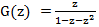
फाइबोनैचि संख्याओं के अनुक्रम के लिए एक जनरेटिंग फ़ंक्शन है।

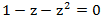
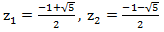
हम इसे सबसे सरल अंशों के योग में विघटित करते हैं, इसके लिए हम समीकरण की जड़ों को खोजते हैं । इस सरल द्विघात समीकरण को हल करते हुए, हमें यह मिलता है: । फिर हमारा उत्पादन कार्य निम्नानुसार विघटित हो सकता है:



अगला चरण गुणांक ए और बी को खोजना है। ऐसा करने के लिए, आम भाजक द्वारा भिन्न को गुणा करें:



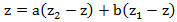
इस समीकरण में मान z = z ₁ और z = z ₂ को प्रतिस्थापित करते हुए, हम पाते हैं

अंत में, हम जनरेटिंग फ़ंक्शन के लिए अभिव्यक्ति को थोड़ा बदल देते हैं



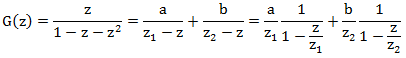
अब प्रत्येक अंश में ज्यामितीय प्रगति का योग है।

सूत्र के अनुसार हम पाते हैं

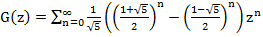
लेकिन हम फॉर्म में जी (z) की तलाश कर रहे थे । इससे हम यह निष्कर्ष निकालते हैं



इस सूत्र को "सुनहरे अनुपात" का उपयोग किए बिना दूसरे रूप में फिर से लिखा जा सकता है:



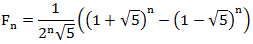
जो सुंदर पुनरावर्ती समीकरण को देखते हुए, उम्मीद करना काफी कठिन था।

आइए जनरेटिंग फ़ंक्शन का उपयोग करके पुनरावृत्ति समीकरणों को हल करने के लिए एक सामान्य एल्गोरिदम लिखें। यह 4 चरणों में लिखा गया है:

1. अनुक्रम के अन्य तत्वों के माध्यम से gn व्यक्त करने वाला एक समीकरण लिखिए। यह समीकरण सभी पूर्णांक n के लिए मान्य होना चाहिए, इस तथ्य को ध्यान में रखते हुए कि जी _-1 = जी _-2 = .... = 0।
   
2. समीकरण के दोनों किनारों को z ⁿ और सभी n पर योग से गुणा करें। बाईं ओर आपको राशि मिलती है , जो जनरेटिंग फंक्शन G (z) के बराबर है। दाईं ओर को रूपांतरित किया जाना चाहिए ताकि यह कुछ अन्य अभिव्यक्ति में बदल जाए जिसमें G (z) शामिल है।
3. जी (जेड) के लिए एक बंद अभिव्यक्ति प्राप्त करके परिणामी समीकरण को हल करें।
4. पावर श्रृंखला में G (z) का विस्तार करें और z ⁿ पर गुणांक पढ़ें, यह g _{n के} लिए एक बंद रूप होगा।

यह विधि काम करती है इसका कारण यह है कि एकल फ़ंक्शन G (z) पूरे अनुक्रम g _n का प्रतिनिधित्व करता है और यह प्रतिनिधित्व कई परिवर्तनों की अनुमति देता है।

अगले उदाहरण पर जाने से पहले, हम उन कार्यों को उत्पन्न करने वाले 2 कार्यों पर विचार करेंगे जो अक्सर उपयोगी होते हैं।

कार्य करने की भिन्नता और एकीकरण

कार्य उत्पन्न करने के लिए, व्युत्पन्न की सामान्य परिभाषा निम्नानुसार लिखी जा सकती है।

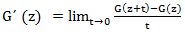
G = G (z) को जनरेटिंग फंक्शन होने दें। इस फ़ंक्शन के व्युत्पन्न को फ़ंक्शन कहा जाता है । भेदभाव स्पष्ट रूप से एक रेखीय ऑपरेशन है, इसलिए, यह समझने के लिए कि यह जनरेटिंग कार्यों पर कैसे कार्य करता है, यह चर की डिग्री में, इसकी कार्रवाई को देखने के लिए पर्याप्त है। हमारे पास है



इस प्रकार, एक मनमाने ढंग से उत्पन्न होने वाले फ़ंक्शन पर भेदभाव की कार्रवाई
G (z) = g ₀ + g ₁ z + g ₂ z ² + g ₃ z ³ + ... देता है G΄ (z) = g ₁ + 2g ₂ z + 3G ₃ z ² + 4g ₄ z ³ + ....

अभिन्न कार्य है



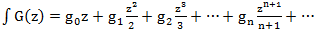
भेदभाव ऑपरेशन एकीकरण ऑपरेशन का उल्टा है:



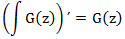
व्युत्पन्न को एकीकृत करने का कार्य एक शून्य मुक्त अवधि के साथ एक फ़ंक्शन की ओर जाता है, और इसलिए परिणाम मूल फ़ंक्शन से भिन्न होता है,



यह देखना आसान है कि बिजली श्रृंखला के रूप में प्रतिनिधित्व करने वाले कार्यों के लिए, व्युत्पन्न के लिए सूत्र सामान्य से मेल खाता है। अभिन्न के लिए सूत्र एक चर ऊपरी सीमा के साथ अभिन्न के मूल्य से मेल खाती है



जनरेटिंग फ़ंक्शंस के भेदभाव और एकीकरण पर प्राप्त ज्ञान का उपयोग करके, हम निम्नलिखित पुनरावृत्ति समीकरण को हल करने का प्रयास करेंगे:

जी ₀ = 1,
जी ₁ = 1,
g _n = g _n-1 + 2g _n-2 + (-1) ⁿ

हम उपरोक्त एल्गोरिथ्म का पालन करेंगे। एल्गोरिथ्म की पहली शर्त संतुष्ट है। हम सभी समानताओं के दोनों पक्षों को z से उचित डिग्री तक जोड़ते हैं और जोड़ते हैं:

z ⁰ ⋅ g ₀ = 1,
z ¹ ⋅ g ₁ = z,
z ^n- g _n = z ⁿ ⋅ g _n-1 + 2z _n- g _n-2 + (-1) ⁿ ) z ⁿ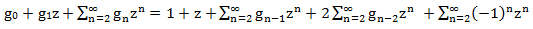



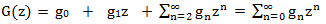
बाईं ओर अनंत रूप में एक उत्पादक कार्य है।

हम G (z) के संदर्भ में दाईं ओर व्यक्त करने का प्रयास करते हैं। प्रत्येक शब्द पर विचार करें:







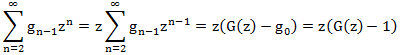
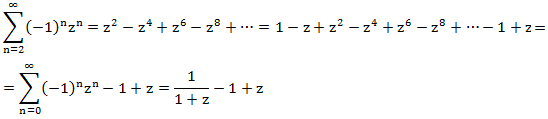
हम समीकरण की रचना करते हैं:



यह किसी दिए गए पुनरावृत्ति समीकरण के लिए जनरेटिंग फंक्शन है। इसे साधारण अंशों में विस्तारित करना (उदाहरण के लिए, अनिश्चित गुणांक की विधि द्वारा या z के विभिन्न मूल्यों को प्रतिस्थापित करने की विधि द्वारा), हम प्राप्त करते हैं:



दूसरे और तीसरे शब्दों को आसानी से एक शक्ति श्रृंखला में विघटित किया जाता है, लेकिन आपको पहले के साथ थोड़ा छेड़छाड़ करना होगा। निर्माण कार्यों के विभेदीकरण के नियम का उपयोग करना, हमारे पास है:



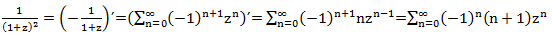
वास्तव में सब कुछ। हम पावर श्रृंखला में प्रत्येक शब्द का विस्तार करते हैं और उत्तर प्राप्त करते हैं:



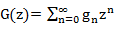
एक ओर, हमने फॉर्म में G (z) की खोज की दूसरी ओर ।

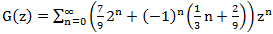
इसलिए, ।

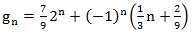
एक निष्कर्ष के बजाय

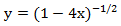
निर्माण कार्यों ने गणित में बहुत अच्छा अनुप्रयोग पाया है, क्योंकि वे संबंधित कई व्यावहारिक समस्याओं को हल करने में शक्तिशाली हथियार हैं, उदाहरण के लिए, विभिन्न प्रकृति की वस्तुओं के सेट, लिस्टिंग, वितरण और तोड़ने के लिए। इसके अलावा, जनरेटिंग फ़ंक्शंस का उपयोग हमें कुछ कॉम्बीनेटरियल फ़ार्मुलों को साबित करने की अनुमति देता है जो अन्यथा प्राप्त करना बहुत मुश्किल है। उदाहरण के लिए, कार्य विघटन एक शक्ति श्रृंखला में रूप है , 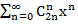अर्थात् समानता सत्य है:



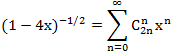
इस समानता के दोनों किनारों पर, हम प्राप्त करते हैं



बाएं और दाएं पक्षों में x ^{n के} लिए गुणांक की समानता, हम प्राप्त करते हैं



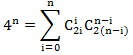
इस सूत्र का एक पारदर्शी संयोजन अर्थ है, लेकिन इसे साबित करना आसान नहीं है। XX सदी के 80 के दशक में इस मुद्दे को समर्पित प्रकाशन थे।