
हर कोई बहुत अच्छी तरह से जानता है कि विनिमय सॉर्टिंग के वर्ग से सबसे तेज़ विधि तथाकथित
त्वरित सॉर्ट है । उनके बारे में शोध प्रबंध लिखे गए हैं, हेबे के कई लेख उनके लिए समर्पित हैं, उनके आधार पर वे जटिल हाइब्रिड एल्गोरिदम के साथ आते हैं। लेकिन आज हम
त्वरित छंटाई के बारे में बात नहीं कर रहे हैं, लेकिन एक अन्य विनिमय पद्धति के बारे में - अच्छा पुराना
बुलबुला छंटाई और इसके सुधार, संशोधन, म्यूटेशन और किस्में।
इन तरीकों से प्रैक्टिकल निकास इतना गर्म नहीं है, और कई habrappolzov यह सब प्रथम श्रेणी में हुआ। इसलिए, लेख उन लोगों को संबोधित किया जाता है जो केवल एल्गोरिदम के सिद्धांत में रुचि रखते हैं और इस दिशा में पहला कदम उठा रहे हैं।
छवि: बुलबुलेआज हम सबसे सरल
छंटनी एक्सचेंजों के बारे में बात करेंगे।
अगर किसी को दिलचस्पी है, तो मैं कहूंगा कि अन्य वर्ग हैं -
चयन द्वारा छँटाई ,
आवेषण द्वारा छँटाई ,
विलय द्वारा छँटाई ,
वितरण द्वारा छँटाई ,
संकर छँटाई और
समानांतर छँटाई । वैसे, वहाँ भी
गूढ़ सॉर्टिंग हैं । ये विभिन्न नकली, मौलिक रूप से अवास्तविक, हास्य और अन्य छद्म एल्गोरिदम हैं, जिनके बारे में मैं किसी तरह आईटी-ह्यूमर हब में कुछ लेख लिखूंगा।
लेकिन इसका आज के व्याख्यान से कोई लेना-देना नहीं है, अब हम केवल आदान-प्रदान के सरल उपायों में रुचि रखते हैं। एक्सचेंजों की बहुत सारी छंटनी भी हैं (मैं एक दर्जन से अधिक जानता हूं), इसलिए हम तथाकथित
बबल सॉर्टिंग और कुछ अन्य लोगों पर विचार करेंगे जो इसके साथ निकटता से जुड़े हुए हैं।
मैं पहले से चेतावनी दूंगा कि उपरोक्त सभी विधियां बहुत धीमी हैं और उनकी समय की जटिलता का कोई गहन विश्लेषण नहीं होगा। कुछ तेज हैं, कुछ धीमी हैं, लेकिन मोटे तौर पर, हम कह सकते हैं कि औसत
ओ (
एन 2 ) पर। इसके अलावा, मैं किसी भी प्रोग्रामिंग भाषा में कार्यान्वयन के साथ लेख को अव्यवस्थित करने का कोई कारण नहीं देखता हूं। रुचि रखने वाले आसानी से
रोसेटा ,
विकिपीडिया, या कहीं और पर कोड उदाहरण पा सकते हैं।
लेकिन वापस आदान-प्रदान करने के लिए। आदेश सरणी के कई अनुक्रमिक गणना और एक दूसरे के साथ तत्वों के जोड़े की तुलना के परिणामस्वरूप होता है। यदि तुलना की गई वस्तुओं को एक दूसरे के सापेक्ष सॉर्ट नहीं किया जाता है, तो हम उन्हें स्वैप करते हैं। एकमात्र सवाल यह है कि सरणी को बिल्कुल कैसे बायपास किया जाए और तुलना के लिए जोड़े का चयन किस सिद्धांत से किया जाए।
आइए संदर्भ बबल सॉर्ट के साथ शुरू न करें, लेकिन एक एल्गोरिथ्म के साथ ...
सिली तरह
छंटनी वास्तव में बेवकूफी है। हम बाईं ओर से सरणी को देखते हैं और रास्ते में पड़ोसियों की तुलना करते हैं। यदि हम पारस्परिक रूप से अनसोल्ड तत्वों की एक जोड़ी को पूरा करते हैं, तो हम उन्हें स्वैप करते हैं और एक वर्ग में लौटते हैं, अर्थात् बहुत शुरुआत तक। हम फिर से गुजरते हैं, सरणी की जांच करते हैं, अगर हम फिर से पड़ोसी तत्वों के "गलत" जोड़े से मिलते हैं, तो हम स्थानों को स्वैप करते हैं और फिर से हम फिर से शुरू करते हैं। हम तब तक जारी रखते हैं जब तक कि सरणी धीरे-धीरे हल न हो जाए।

"तो कोई भी मूर्ख जानता है कि कैसे छाँटना है" - आप कहते हैं, और आप बिल्कुल सही होंगे। इसीलिए छंटाई को "बेवकूफ" कहा जाता था। इस व्याख्यान में, हम इस पद्धति को लगातार सुधारेंगे और संशोधित करेंगे। अब उसके पास समय जटिलता
O (
n 3 ) है, एक सुधार करने के बाद, हम इसे
O (
n 2 ) में लाएंगे, फिर हम इसे थोड़ा गति देंगे, फिर से, और अंत में हमें
O (
n log
n ) मिलेगा - और यह होगा नहीं "त्वरित क्रमबद्ध करें"!
हम बेवकूफ प्रकार में एक ही सुधार जोड़ेंगे। मार्ग के दौरान और उनके स्थानों का आदान-प्रदान करने के दौरान दो आसन्न अनसुलझे तत्वों की खोज करने के बाद, हम सरणी की शुरुआत में वापस नहीं आएंगे, लेकिन शांतिपूर्वक इसे बहुत अंत तक बायपास करते रहेंगे।
इस मामले में, हमारे सामने सब कुछ ज्ञात नहीं है ...
बबल सॉर्ट
या
साधारण आदान-प्रदान द्वारा छँटाई । शैली की अमर क्लासिक्स। कार्रवाई का सिद्धांत सरल है: हम शुरुआत से अंत तक सरणी के चारों ओर जाते हैं, साथ ही साथ पड़ोसी तत्वों को स्वैप करते हैं। पहले पास के परिणामस्वरूप, अधिकतम तत्व अंतिम स्थान पर "पॉप अप" होता है। अब फिर से हम ऐरे के पहले भाग (पहले तत्व से लेकर तदनुरूप) के चारों ओर घूमते हैं और अनसोल्ड पड़ोसियों के मार्ग को बदलते हैं। दूसरा सबसे बड़ा तत्व प्रायद्वीप में होगा। उसी शिरा में जारी रखते हुए, हम सरणी के कभी-कभी घटते हुए अनसरेक्टेड हिस्से को बायपास करेंगे, जो कि मिली मैक्सिमा को अंत तक धकेल देगा।

यदि हम ऊंचाइयों को न केवल अंत तक धकेलते हैं, बल्कि शुरुआत में चढ़ाव को स्थानांतरित करने के लिए, तो हम प्राप्त करते हैं ...
शेकर तरह
वह
मिक्स करके सॉर्ट कर रहा है , वह
कॉकटेल सॉर्ट कर रहा है । प्रक्रिया एक "बुलबुले" के रूप में शुरू होती है: अधिकतम बैकयार्ड के लिए अधिकतम निचोड़ें। उसके बाद, 180
0 के आसपास मुड़ें और विपरीत दिशा में जाएं, जबकि पहले से ही शुरुआत में रोलिंग अधिकतम नहीं है, लेकिन न्यूनतम है। सरणी में पहले और अंतिम तत्वों को क्रमबद्ध करने के बाद, हम फिर से सोमरस करते हैं। आगे और पीछे कई बार जा रहे हैं, अंत में हम इस प्रक्रिया को समाप्त करते हैं, जो सूची के मध्य में है।

शेबर सॉर्टिंग बबल सॉर्टिंग की तुलना में थोड़ा तेज काम करता है, क्योंकि मैक्सिमा और मिनिमा बारी-बारी से सही दिशाओं में सरणी के साथ पलायन करते हैं। सुधार, जैसा कि वे कहते हैं, स्पष्ट हैं।
जैसा कि आप देख सकते हैं, यदि हम खोज प्रक्रिया को रचनात्मक रूप से देखते हैं, तो भारी (प्रकाश) तत्वों को सरणी के सिरों पर धकेलना अधिक तेज़ है। इसलिए, कारीगरों ने सूची को एक और गैर-मानक "रोड मैप" को बायपास करने का प्रस्ताव दिया।
विचित्र-समान
इस बार हम आगे और पीछे के सरणी के बारे में नहीं सोचेंगे, लेकिन फिर से हम योजनाबद्ध दौर की यात्रा पर बाएं से दाएं पर विचार करेंगे, लेकिन केवल एक व्यापक कदम उठाएँ। पहले पास पर, हम पड़ोसियों के साथ एक विषम कुंजी वाले तत्वों की तुलना करते हैं, यहां तक कि पड़ोसी स्थानों पर रहने वाले (1 वाले की तुलना 2 के साथ की जाती है, फिर 4 के साथ 3 जी, 6 वें के साथ 5 वें और इतने पर)। फिर, इसके विपरीत, हम "विषम" वाले तत्वों में "यहां तक कि गिनती में" की तुलना / परिवर्तन करते हैं। फिर से "विषम-सम", फिर "विषम-सम"। प्रक्रिया तब रुक जाती है, जब दो क्रमिक सरणी ("विषम-सम" और "सम-विषम") से गुजरने के बाद, कोई विनिमय नहीं हुआ। तो, हल किया।

प्रत्येक पास के दौरान सामान्य "बबल" में, हम सरणी के अंत में व्यवस्थित रूप से अधिकतम को निचोड़ते हैं। यदि आप सम और विषम सूचक साथ छोड़ते हैं, तो तुरंत सरणी के सभी अधिक या कम बड़े तत्वों को एक साथ एक रन में एक स्थिति से दाईं ओर धकेल दिया जाता है। यह तेजी से निकलता है।
हम अंतिम
संक्षिप्त नाम *
Sortuvannya bulbashka ** -
Sortuvannya रोइंग *** के लिए
विश्लेषण करेंगे। यह विधि बहुत चालाकी से आदेश देती है,
O (
n 2 ) इसकी सबसे खराब जटिलता है। औसतन, हमारे पास समय में
O (
n लॉग
एन ) है, और सबसे अच्छा आप यह मानते हैं कि यह
O (
n ) है। यही कारण है कि, "त्वरित प्रकार" के सभी प्रकार के लिए एक बहुत ही योग्य प्रतियोगी है और यह, आप पर ध्यान दें, पुनरावृत्ति के उपयोग के बिना। हालाँकि, मैंने वादा किया था कि आज हम क्रूर गति में नहीं जाते हैं, हम चुपचाप सीधे एल्गोरिथम तक जाते हैं।

कछुए को दोष देना है
थोड़ी पृष्ठभूमि। 1980 में, Vlodzimezh Dobosievich ने बताया कि बबल और इसके डेरिवेटिव्स को इतनी धीमी गति से क्यों काम किया जाता है।
यह सब कछुओं की वजह से है । कछुए छोटे आइटम हैं जो सूची के अंत में हैं। जैसा कि आपने देखा होगा कि बबल सॉर्टिंग "खरगोश" (बाबुस्किन की "दादी" के साथ भ्रमित नहीं होना) के लिए उन्मुख हैं, जो सूची की शुरुआत में बड़े तत्व हैं। वे बहुत तेजी से फिनिश लाइन की ओर बढ़ रहे हैं। लेकिन धीमी गति से सरीसृप शुरू में अनिच्छा से रेंगना। आप एक
कंघी के साथ tortillas को अनुकूलित कर सकते हैं।
छवि: दोषी कछुआहेयरब्रश को क्रमबद्ध करें
"बबल", "शेकर" और "ऑड-ईवन" में, जब ऐरे के ऊपर चलना होता है, तो पड़ोसी तत्वों की तुलना की जाती है। "कंघी" का मुख्य विचार शुरू में तुलना किए गए तत्वों के बीच पर्याप्त रूप से बड़ी दूरी तय करना है और सरणी के आदेश के अनुसार दूरी को न्यूनतम तक सीमित करना है। इस प्रकार, हम सरणी को कंघी कर रहे हैं, जैसा कि यह था, धीरे-धीरे इसे और अधिक साफ किस्में में चिकना करना।

तुलनात्मक तत्वों के बीच प्रारंभिक अंतर को किसी भी तरह से लेना बेहतर है, लेकिन
कमी कारक नामक एक विशेष मूल्य को ध्यान में रखते हुए, जिसका इष्टतम मूल्य लगभग 1.247 है। सबसे पहले, तत्वों के बीच की दूरी
कमी कारक द्वारा विभाजित सरणी के आकार के बराबर है (परिणाम, निश्चित रूप से, निकटतम पूर्णांक तक गोल है)। फिर, इस चरण के साथ सरणी को पास करने के बाद, हम फिर से कदम
को कम करने वाले कारक से विभाजित करते हैं और फिर से सूची से गुजरते हैं। यह तब तक जारी रहता है जब तक कि सूचकांकों में अंतर एकता तक नहीं पहुंच जाता। इस मामले में, सरणी को एक नियमित बुलबुले के साथ हल किया जाता है।
प्रयोगात्मक और सैद्धांतिक रूप से,
कमी कारक का इष्टतम मूल्य स्थापित किया
गया था:
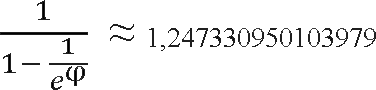
जब इस पद्धति का आविष्कार किया गया था, तो कुछ लोगों ने 70 और 80 के दशक के जंक्शन पर इस पर ध्यान दिया। एक दशक बाद, जब प्रोग्रामिंग अब आईबीएम वैज्ञानिकों और इंजीनियरों की चिंता का विषय नहीं था, और पहले से ही बड़े पैमाने पर चरित्र का हिमस्खलन हो रहा था, 1991 में स्टीफन लैसी और रिचर्ड बॉक्स द्वारा इस पद्धति को फिर से खोजा, अनुसंधान और लोकप्रिय बनाया गया।
यह वास्तव में वह सब है जो मैं आपको बुलबुला छंटाई और इसके ilk के बारे में बताना चाहता था।
- नोट्स* संक्षिप्त नाम (
यूक्रेनी ) - सुधार
** Sortuvannya Bulbashka (
यूक्रेनी ) - बुलबुला द्वारा क्रमबद्ध करें
*** एक कंबाइन (
यूक्रेनी ) द्वारा Sortuvannya - एक कंघी द्वारा छंटनी