डिजीटल चित्रों की तुलना करते समय इष्टतम स्थिति का पता लगाना

लेख डिजीटल (स्कैन) छवियों की तुलना करने के कार्य का वर्णन करता है।

एक संदर्भ छवि के समानांतर हस्तांतरण के लिए खोज की समस्या का एक सैद्धांतिक समाधान प्रस्तुत किया गया है, जिसमें परीक्षण की गई छवि के साथ इसका मिलान अधिकतम है। द्विआधारी डिजीटल प्रतीकों की पारियों के विश्लेषण से संबंधित कम्प्यूटेशनल प्रयोगों का वर्णन किया गया है। एक तुलना बाइनरी डिजिटाइज्ड प्रतीकों के वर्ग पर विचार करते समय किसी अन्य और वास्तविक पारियों के सापेक्ष एक ग्राफिक छवि के संभावित बदलाव की रचनात्मक रूप से गणना की गई सीमा से की जाती है।

परिचय

कई मान्यता एल्गोरिदम में, दो बाइनरी छवियों की तुलना कुछ निकटता फ़ंक्शन का उपयोग करके यह समझने के लिए की जाती है कि वे दो "समान" वस्तुओं की छवियां हैं या नहीं। निकटता फ़ंक्शन को चुना जाता है ताकि मान्यता एल्गोरिथ्म की आवश्यकताओं को पूरा किया जा सके और किसी दिए गए स्रोत से प्राप्त छवियों की विशेषताओं को ध्यान में रखा जा सके।

हम छवियों के स्थान पर विचार करते हैं जिसे यू ने मैट्रिक्स आर = के रूप में दर्शाया है आर _आईजे || समान आकार 0 ≤ i , m , 0 ≤ j ≤ n । वास्तविक छवि के आयाम मैट्रिक्स मी के आयामों की तुलना में काफी छोटे हैं एन। आयामों के साथ छवि का स्थान m _१ आयाम _{1 के} साथ मैट्रिक्स में n ₁ ( एम ₁ < m , n ₁ < n ) n को सेंट्रिंग कहा जाएगा । यदि वास्तविक छवि मैट्रिक्स m ₁ द्वारा दर्शाई जाती है एन ₁ , तो यह संभव है, उदाहरण के लिए, इस छवि को केंद्र में रखना ताकि मैट्रिस एम ₁ के केंद्र एन ₁ और एम n मैच। आप केंद्र के अन्य तरीकों के बारे में सोच सकते हैं और लागू कर सकते हैं, हमारे लिए यह महत्वपूर्ण है कि सभी छवियों के लिए केंद्र की विधि समान हो।

जब छवियों को क्लस्टर करना और उन्हें पहचानना, एक गैर-नकारात्मक निकटता फ़ंक्शन d का उपयोग किया जाता है , जो दो छवियों की तुलना करता है A = || एक _आईजे || और बी = || b _ij ||, ए यू , बी यू सम्मेलन द्वारा, हम छवि A को संदर्भ कहेंगे, और B परीक्षण को एक । जब डिजिटल उपकरणों (स्कैनर, कैमरा और वीडियो कैमरा) का उपयोग करके छवियां प्राप्त की जाती हैं, तो कई अंकीयकरण प्रभाव पैदा होते हैं। इन प्रभावों में सबसे सरल यह है कि एक प्रोटोटाइप से, ऐसे चित्र प्राप्त किए जा सकते हैं जो आपस में और प्रोटोटाइप के साथ भिन्न हों। यह प्रोटोटाइप और डिजिटल ग्रिड (उदाहरण के लिए, स्कैनर ग्रिड) के संयोजन के संयोग से समझाया गया है और 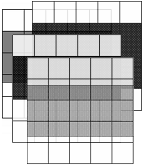चित्र 1 में चित्रित किया गया है, जो दिखाता है कि एक स्रोत प्रोटोटाइप (ग्रे स्ट्रिप) से दो अलग-अलग डिजिटाइज़ बाइनरी इमेज (काली पट्टियाँ) कैसे प्राप्त की जाती हैं।

चित्रा 1 - स्कैनर ग्रिड पर विभिन्न ओवरले के साथ एक छवि को डिजिटल करने के उदाहरण
(ग्रे धारियों - प्रोटोटाइप, काली - द्विआधारी चित्र)

निकटता और मान्यता में प्रयुक्त निकटता समारोह की दो आवश्यकताएं हैं:

• स्वयंसिद्ध पहचान - d ( A , B ) = 0 ए = बी ;
• समरूपता का स्वयंसिद्ध शब्द - d ( A , B ) = d ( B , A ) ए , बी।

बाइनरी छवियों की तुलना करते समय डिजिटलीकरण प्रभाव का योगदान निकटता फ़ंक्शन को चुनकर और शिफ्ट प्रक्रिया को लागू करके कम से कम किया जाता है। इस पत्र में, हेमिंग मेट्रिक को एक निकटता फ़ंक्शन के रूप में माना जाता है।

।

अंतरिक्ष A से छवियों A और B की तुलना करते समय , हम छवि A = की सभी प्रकार की शिफ्ट करेंगे एक _आईजे || अलग-अलग दिशाओं में और परिणामस्वरूप छवि और बी के बीच निकटता फ़ंक्शन पर विचार करें । हम मैट्रिक्स ए की पारी को मूल्य ( एच , डब्ल्यू ) के रूप में परिभाषित करते हैं



दूसरे शब्दों में, ए ( एच , डब्ल्यू ) को टोरस पर वेक्टर ( एच , डब्ल्यू ) में स्थानांतरण के परिणामस्वरूप प्राप्त किया जाता है, जो आयाम एम के साथ एक आयत के क्षेत्र का समापन है n ( चित्र 2 देखें)

चित्रा 2 - प्रतीक "एम" की छवि को टोरस पर विभिन्न वैक्टरों में स्थानांतरित करने के उदाहरण

अब हम छवियों A और B के बीच "दूरी" d ₀ निर्धारित कर सकते हैं ।

(1)

मैट्रिक्स ए ( एच , डब्ल्यू ) जिस पर न्यूनतम पहुंच गया है, उसे ए के सापेक्ष ए की छवि की इष्टतम स्थिति कहा जाएगा, और वेक्टर ( एच , डब्ल्यू ) को इष्टतम पारी कहा जाएगा।

डी ₀ ( ए , बी ) और इष्टतम बदलाव ( एच , डब्ल्यू ) निर्धारित करने के लिए विभिन्न तरीके हैं।
सबसे सरल में से एक निकटता फ़ंक्शन डी ( एच , डब्ल्यू ) = की गणना करना है ( ए ( एच , डब्ल्यू ), बी )), एच और डब्ल्यू के मूल्यों को सीमित करना: एच ₀ एन _० , डब्ल्यू । एन _० ।

सामान्यतया, n ₀ का सबसे छोटा मान, यह गारंटी देता है कि वास्तविक न्यूनतम d ( h , w ) प्राप्त किया गया है, पहले से ज्ञात नहीं है, n ₀ की ऊपरी सीमा को शिफ्ट की मात्रा से निर्धारित किया जाता है, जिस पर चित्र A और B प्रतिच्छेद नहीं करते हैं, अर्थात, _ij ब _इज = ० मैं और जे। ऐसे n _{0 के लिए,} d ₀ ( h , w ) निर्धारित करने _की विधि सटीक है। एन ₀ के मानों के लिए जो वास्तविक न्यूनतम डी ( एच , डब्ल्यू ) की उपलब्धि की गारंटी नहीं देते हैं, इष्टतम स्थिति निर्धारित करने की विधि अनुमानित है और किसी को कुछ त्रुटि के साथ डी ₀ ( ए , बी ) की गणना करने की अनुमति देता है।

हम मानते हैं, हालांकि, कि ए की छवि की प्रारंभिक स्थिति, जिसे आमतौर पर संयोग से किसी भी तरह से नहीं चुना जाता है, को इष्टतम से बहुत दूर नहीं होना चाहिए। अधिक सटीक रूप से, यदि यादृच्छिक रूप से लिया गया स्थान सफल है, अर्थात। यदि संदर्भ और परीक्षण चित्र मेल नहीं खाते हैं ( ए , बी ), संदर्भ छवि का एक छोटा सा हिस्सा है, फिर समानांतर स्थानांतरण ( एच , डब्ल्यू ), छवियों के संयोग को अधिकतम करना, छोटा है (यानी, संदर्भ छवि के व्यास का एक छोटा हिस्सा है)।

वास्तव में, यह इस आशय का है कि विचाराधीन वैक्टर ( एच , डब्ल्यू ) को प्रतिबंधित करने का औचित्य है।
यह स्पष्ट है कि छोटा n ₀ , डी = मिनट _{एच, डब्ल्यू} डी ( एच , डब्ल्यू ) की गणना करने में कम समय लगेगा, लेकिन मैं दो छवियों की तुलना करते समय कतरनी के प्रभाव के कुछ प्रकार के अनुमान लगाना चाहूंगा और, एक निश्चित स्थिति की निकटता का आकलन कर रहा हूं। इष्टतम के लिए छवि। वर्तमान कार्य ऐसे अनुमानों को प्राप्त करने के लिए समर्पित है।

पहला खंड, जो कार्य का विकास है, एक सैद्धांतिक विश्लेषण देता है। दूसरे खंड में - सबसे लोकप्रिय मान्यता कार्यों में से एक की वस्तुओं पर प्रयोग - रूसी वर्णमाला के प्रतीक।

1. छवियों की तुलना करते समय बदलाव के प्रभाव का अध्ययन

1.1। कार्य विवरण

नीचे एक गणितीय मॉडल है जो एक गुणात्मक स्तर पर उपरोक्त प्रभाव की व्याख्या कर रहा है। उसी समय, हम प्रारंभिक सेटिंग्स को महत्वपूर्ण रूप से विस्तारित करेंगे। मॉडल में, छवि को एक जोड़ी के रूप में माना जाता है जिसमें सेट I (नॉनज़ेरो इमेज पॉइंट्स) और घनत्व image: I → R (छवि बिंदुओं के भार का वितरण) शामिल होता है। घनत्व φ ₁ और model _{2 के} साथ छवि के संयोग की डिग्री को अभिन्न द्वारा मॉडलिंग की जाती है ।

चलो माप d σ और X वाला स्थान युग्मों x = ( I ,,) का समूह है, जहाँ मैं एक औसत दर्जे का सबसेट है और I : I → R एक पूर्णांक गैर-नकारात्मक फ़ंक्शन है जिसे घनत्व कहा जाता है। सेट X पर एक मीट्रिक परिभाषित किया गया है जहाँ

चलो γ: → एक-से-एक मैपिंग एक माप को संरक्षित करता है, अर्थात। σ * d d = d σ। नक्शा। आइसोमेट्री को प्रेरित करता है बिंदु x = ( I , () को बिंदु पर ले जाना । निर्वाह करके और संख्या Y का सबसेट परिभाषित करें X अंक ( I , φ) से मिलकर बनता है जैसे:

1. मैं
2. 

टास्क 1. फंक्शन के लिए सबसे अच्छा (सबसे अच्छा) लोअर बाउंड।

समस्या 1 का एक संभावित उत्तर अगले पैराग्राफ में वर्णित है।
आइए हम समस्या 1 के एक संशोधन पर ध्यान दें।

सेट एक्स को बढ़ाएं और सेट को परिभाषित करें जोड़े से मिलकर जिसमें घनत्व। को बिंदुओं पर केंद्रित किया जा सकता है। अधिक सटीक, सेट में सामान्यीकृत घनत्व φ, जो पूर्णांक कार्यों के योग हैं और बिंदु q पर δ-फ़ंक्शन के परिमित रैखिक संयोजन हैं, घनत्व के रूप में माना जाता है (हम उन्हें) _q द्वारा निरूपित करेंगे), अर्थात। । अंतरिक्ष के लिए दूरी, प्रदर्शन परिभाषाएँ स्वचालित रूप से स्थानांतरित हो जाती हैं और फ़ंक्शंस which, जिसे हम क्रमशः निरूपित करते हैं, , और । मानचित्रण γ दिया जाए: → के एक सबसेट और संख्या । एक उपसमुच्चय दें अंक के होते हैं जहाँ ऐसा है कि:

1. मैं ।
2. ≥ ≥ 0, ≥ 0, फ़ंक्शन का समर्थन φ I और q _k में निहित है मैं,
3. ;

टास्क 1 '। कार्य के लिए सबसे अच्छा (सबसे अच्छा) लोअर बाउंड।

1.2। समस्या का आंशिक समाधान १

निम्नलिखित प्रमेय रखती है।

प्रमेय 1. यदि, कुछ पूर्णांक n के लिए, सेट ( ⁿ ( ) सेट के साथ प्रतिच्छेद नहीं करता है तो ।

सबूत। बिंदु y के साथ Y हम संबंधों द्वारा परिभाषित X में अनुक्रम y ₀ , y ₁ , ..., y _n अंक को जोड़ते हैं

आज्ञा देना y = ( I ,,)। वाई के बाद से Y तब ।

इसलिये
।

मैपिंग के बाद से एक सममिति है, तो किसी भी k के लिए हमारे पास है ।

एक त्रिकोण के स्वयंसिद्ध द्वारा यानी । जिसे सिद्ध करना आवश्यक था।

हम बताते हैं कि कुछ अतिरिक्त परिस्थितियों में प्रमेय 1 से अनुमान में सुधार नहीं किया जा सकता है। मुख्य एक निम्नलिखित स्थिति है।

शर्त : एक बिंदु क्ष है ऐसे कि अंक γ ⁿ ( q ) के अपवाद के साथ अंक q ,) ( q ), ... q ⁿ ( q ) अलग हैं और वे सभी, सेट में हैं ।

मान लीजिए कि आगे सेट है एक टोपोलॉजी से लैस है जिसमें सेट है खुला और नक्शा map निरंतर है।

प्रमेय 2. मान लीजिए कि उपरोक्त शर्तें संतुष्ट हैं और । तो ।

सबूत। स्थिति को संतुष्ट करने वाला एक बिंदु q चुनें , और इसके पड़ोस E को सकारात्मक माप के रूप में लें, इतना छोटा कि प्रत्येक k = 0, 1, ..., n के लिए, पड़ोस do ⁿ ( E ) एक दूसरे को और उन सभी को प्रतिच्छेद न करें, सिवाय पड़ोस γ ⁿ ( q ) के, झूठ सेट । आज्ञा देना Let ₀ पर एक गैर-नकारात्मक कार्य है जिसका समर्थन क्षेत्र ई में निहित है ।

आज्ञा देना x = ( I , φ) एक बिंदु है निम्नलिखित रिश्तों द्वारा परिभाषित:



तो

।

हमारे पास है

।

यह देखना आसान है

।

इसलिए, ≤ ≤ 2 a / n । प्रमेय 1 के द्वारा,, a 2 a / n । प्रमेय २ सिद्ध होता है ।

समस्या 1 का आंशिक समाधान । ' प्रमेय 1 को वस्तुतः समस्या 1 के मामले में सामान्यीकृत किया गया है। हम इस सामान्यीकरण के सूत्रीकरण और प्रमाण पर ध्यान नहीं देंगे। समस्या 1 के मामले के लिए प्रमेय 2 को मजबूत किया जा सकता है: इसके लिए जरूरी नहीं कि इसके अतिरिक्त सेट की भी आवश्यकता हो एक टोपोलॉजी से लैस था जिसमें कई खुला और नक्शा map निरंतर है।

प्रमेय 2 '। हालत होने दो और । तो ।

इसे साबित करने के लिए, इस बिंदु पर विचार करने के लिए पर्याप्त है अंकों के सेट के बराबर δ-फ़ंक्शन के बराबर घनत्व वाले घनों से गुणा किया जाता है / एन । प्रमेय 2 का और प्रमाण 'प्रमेय 2 के प्रमाण के समान है।

1.3। यूक्लिडियन स्पेस का मामला

जगह दें माप ucl के साथ अंतरिक्ष आर ⁿ है यूक्लिडियन माप के साथ, नक्शा a एक निश्चित वेक्टर द्वारा एक पारी है आर ^एन (यानी, γ ( एक्स ) = एक्स + ए ), और सेट यह R ⁿ का कोई भी n- आयामी उत्तल उपसमूह है। गैर-नकारात्मक पूर्णांक कार्यों के सेट पर विचार करें equal R ^{n में} समान रूप से उत्तल सेट के बाहर शून्य के बराबर है और अनुपात को संतुष्ट करना:



यूक्लिडियन स्पेस के लिए समस्या 1 । फ़ंक्शन के लिए सबसे अच्छा (सर्वोत्तम) निचला बाउंड खोजें) ( । , ए) सूत्र द्वारा दिया गया:



समस्या 1 'विचाराधीन मामले में भी इसी तरह तैयार की गई है।

वेक्टर a R ⁿ हम a = के रूप में लिखेंगे a | ν, जहां ν एक इकाई लंबाई वेक्टर है और | ए | वेक्टर की लंबाई है a । इकाई लंबाई के एक वेक्टर ν के लिए, हम ν- व्यास d _{v कहते हैं} ( ) उत्तल आकृति खंडों की लंबाई के समुच्चय का सटीक ऊपरी भाग जो क्षेत्र के खंड हैं वेक्टर ν के समानांतर रेखाएँ। नॉनजरो वेक्टर के लिए a = | a | ν को ए-व्यास d _a कहा जाता _है ( ) उत्तल आकृति संबंध d _v ( ) / | ए | इसकी ν-व्यास लंबाई तक | ए | वेक्टर a ।
हम वेक्टर 1 a के लिए समस्याओं का समाधान 1 और 1 'देते हैं a । ν मामले में जब आंकड़ा का व्यास होता है प्राकृतिक संख्या नहीं।

प्रमेय 3. यदि कुछ पूर्णांक के लिए n in 0 असमानताएं n | a | <डी _वी ( ) <(n + 1) | a, फिर 2 = 2 | / (एन + 1)।

सबूत। प्रमेय 3 की शर्तों के तहत, हमारे पास है । इसलिए, प्रमेय 1 के अनुसार, असमानता ≥ or 2 / ( एन +1)। चूंकि क्षेत्र के क्रॉस सेक्शन की लंबाई पर सटीक ऊपरी बाध्य है वेक्टर ν के समानांतर रेखाओं की तुलना में संख्या n | a |, तब डोमेन के अंदर एक बिंदु y कड़ाई से मौजूद होता है इस तरह के सभी बिंदु y , y + a, ..., y + na बिल्कुल सख्ती से अंदर होते हैं । प्रमेय 2 के द्वारा, हमारे पास,, 2 है / ( n + 1), थ्योरम 3 का अनुसरण करता है।

हम वेक्टर 1 के लिए समस्या 1 का समाधान देते हैं a = | a । ν मामले में जब आंकड़ा का व्यास होता है एक प्राकृतिक संख्या है।

प्रमेय 4. यदि कुछ पूर्णांक n equal 0 के लिए समानता n | a | <डी _वी ( ), तब ।

प्रमेय 4 का प्रमाण प्रमेय के प्रमाण के समान है। 3. यदि समानता n | ए | < डी _वी ( ), तो सामान्य कार्यों पर समस्या में न्यूनतम हासिल नहीं किया जाता है। हालांकि, न्यूनतम functions-फ़ंक्शन के रैखिक संयोजन पर पहुंच जाता है, और यह 2 के बराबर है / ( एन +1)।

1.4। रेटिंग का परिणाम मिला

फ़ंक्शन के लिए सूत्र ε ( । , ए ) बल्कि बोझिल है। कोरोलरी 1 इस फ़ंक्शन का एक गलत लेकिन काफी अच्छा अनुमान देता है, जो काफी अवलोकन योग्य है। कोरोलरी 2 इस फ़ंक्शन का एक अनुमान प्रदान करता है, जो लंबाई के छोटे मूल्यों के लिए एक निश्चित वेक्टर ν के लिए है | ए | लंबाई में रैखिक | ए |, यानी λ के बराबर | ए | एक स्पष्ट रूप से लिखित स्थिर λ के साथ।

कोरोलरी 1. अनुमान उचित है।



यह अनुमान इसके लिए सटीक है - a! = D _v ( ), डी _वी ( ) / 2, डी _वी ( ) / 3, ... और के रूप में | a | → that (जो कि, आलंकारिक रूप से बोल रहा है, यह सटीक है | - a = = d _v (a) ) / ०)।

यदि ε ( । , ए) <2 , तो इस असमानता को फार्म में फिर से लिखा जा सकता है:



कोरोलरी 2. किसी भी y 0 for 0 के लिए 0 any | a | | Have y ₀ हमारे पास है



के लिए | ए | Have y ₀ हमारे पास है



विशेष रूप से, y 0 = d _{v के लिए} ( ) हम निम्नलिखित प्राप्त करते हैं: 0 के लिए a | ए | ≤ डी _वी ( ) हमारे पास है



के लिए | ए | > डी _वी ( ) हमारे पास ε ( । , ए) ≥ (ध्यान दें, वास्तव में, के लिए | a |> d _v ) ) समानता the ( । , ए)) = 2 )।

सबूत। कोरोलरी 1 अपने आप थ्योरम 3 से और 4. कोरोलरी 2 कोरोलरी 1 से अनुसरण करता है।

1.5। प्रश्न में प्रभाव की गुणात्मक व्याख्या

Let (x) उत्तल सेट के बाहर R ⁿ पर शून्य के बराबर एक गैर-नकारात्मक पूर्णांक फ़ंक्शन है । चलो



R ⁿ पर g (x) एक और गैर-नकारात्मक पूर्णांक फ़ंक्शन है। चलो

(2)

मान लिया कि अभिन्न से काफी कम है ।

समस्या 2. पैरामीटर बदलना आर ^एन , सुनिश्चित करें कि अभिन्न

जितना संभव हो उतना छोटा मूल्य लिया।

हमारा लक्ष्य यह दिखाना है कि यदि >> , तो संख्या को कम करने के लिए a ( ए ), केवल वेक्टर की लंबाई के साथ छोटा a = | a | ν, जो ν- व्यास d _v से बहुत कम है ( ) क्षेत्रों ।

हम फ़ंक्शन को define ( ए ) के रूप में परिभाषित करते हैं

, जहां न्यूनतम सभी गैर-नकारात्मक कार्यों से अधिक लिया जाता है 2 संतोषजनक संबंध (2) और क्षेत्र में एक समर्थन है ।
हम ऊपर पाए गए फ़ंक्शन ε ( a ) के अनुमानों को लागू कर सकते हैं।

प्रमेय 5. हम इकाई की लंबाई के एक वेक्टर ν को ठीक करते हैं। D (ν) की न्यूनतम संख्या ऐसी है कि वेक्टर के लिए a = | a | ν, for | a | > d (ν), असमानता a (a)> २ ।
फिर के लिए | ए | > d (ν) असमानता

।
विशेष रूप से, ψ (ए) को कम करने के लिए, यह केवल वैक्टरों पर विचार करने के लिए पर्याप्त है a = | a | ν, जिसमें से | a | <d (ν) ।

सबूत। यह एक त्रिकोण के स्वयंसिद्ध से बहती है। वास्तव में, हमारे पास है


जहां पर | a |> d (ν)

, आवश्यकतानुसार।

कोरोलरी 3. लाइन पर इंटीग्रल minimize (a) को कम करने के लिए a = | a | ν वेक्टर वेक्टर द्वारा फैलाया जाता है, यह केवल वैक्टर पर विचार करने के लिए पर्याप्त है जिसके लिए असमानता

(3)

पर निष्पक्ष असमानता

।

सबूत। यह प्रमेय 5 और कोरोलरी 1 से आता है।

कोरोलरी 3 चर्चा के तहत प्रभाव का गुणात्मक स्पष्टीकरण प्रदान करता है। वास्तव में, यदि >> फिर संख्या / ( - ) पर्याप्त नहीं है। इसलिए, वेक्टर की लंबाई व्यास d _v (a) से बहुत छोटी होने पर न्यूनतम (( a ) प्राप्त होता है। ) के आंकड़े वेक्टर ν की दिशा में। इस प्रकार, यह साबित हो गया है कि दो आंकड़ों की "इष्टतम" स्थिति को प्राप्त करने के लिए, छोटी पारियों के मामले में पर्याप्त है जब छोटे बदलावों में बेमेल का माप नगण्य है।

2. प्रयोग

2.1। स्रोत ऑब्जेक्ट, पैरामीटर और एल्गोरिदम

सिद्ध प्रमेय न्यूनतम दूरी प्राप्त करने के लिए दूसरे के सापेक्ष एक ग्राफिक छवि के संभावित बदलाव की रचनात्मक गणना की गई सीमा देते हैं। यह समझना दिलचस्प है कि किसी विशेष वर्ग की वस्तुओं पर विचार करते समय वास्तविक पारियों को क्या प्राप्त किया जाएगा। हम उन प्रयोगों के परिणाम प्रस्तुत करते हैं जिनमें एक नियमित पुस्तक के पृष्ठ की स्कैन की गई छवि से लिए गए मुद्रित वर्ण वस्तुओं के रूप में काम करते हैं।

तो, स्रोत सामग्री एक परीक्षण सेट है जिसमें रूसी भाषा के अक्षरों के 1770 चित्र शामिल हैं। संकेतों के विभिन्न जोड़े माने जाते हैं, कुल 1770 (1770-1) / 2 = 1565565 जोड़े।

हम एक दूसरे के सापेक्ष दो छवियों ए ₁ और ए ₂ की प्रारंभिक (शून्य) स्थिति निर्धारित करने के लिए कुछ एल्गोरिदम एएल ₁ का उपयोग करेंगे। इस स्थिति में हेमिंग मीट्रिक पर आधारित निकटता फ़ंक्शन के मूल्य को निरूपित किया जाएगा ( ए _१ , ए _२ )। इसके अलावा, हम अनुकूलन एल्गोरिथ्म AL _{0 पर} विचार करेंगे। यह एल्गोरिथ्म प्रारंभिक स्थिति के सापेक्ष विभिन्न वैक्टर ( एच , डब्ल्यू ) में छवियों में से एक के विभिन्न समानांतर हस्तांतरणों की गणना करता है और एक का चयन करता है जिस पर हैमिंग मेट्रिक न्यूनतम मूल्य लेता है। हम इस ₀ ( ए ₁ , ए ₂ ) और अनुकूलन वेक्टर ( एच , डब्ल्यू ) द्वारा ए ( ए ₁ , ए ₂ ) = द्वारा इस (इष्टतम) मूल्य को निरूपित करेंगे। a | ν, जहां ν इकाई दिशा वेक्टर है। आमतौर पर हम मात्रा n ( A ₁ , A ₂ ) = [ a ( A ₁ , A ₂ )] पर विचार करेंगे, जो पिक्सेल में शून्य और इष्टतम स्थिति के बीच की दूरी की विशेषता है।

छवि A के नॉनज़ेरो पिक्सेल की संख्या को निरूपित किया जाएगा । जैसा कि पिछले भाग में दिखाया गया है, संबंध एक महत्वपूर्ण भूमिका निभाता है। / । इसके अलावा, सभी मामलों में जब यह छवियों ए ₁ और ए ₂ की एक जोड़ी की बात आती है, तो मूल्य / ₁ और / ₂ सममित हैं, हम मात्रा पर विचार करेंगे ( ए ₁ , ए ₂ ) = मिनट ( / ₁ / _२ )।

विशेष रूप से, यह कार्य x (x) और g (x) के कार्यों से संबंधित धारा १.५ में सूत्रों को "संतुलित" करता है।
इससे बड़े मूल्यों पर विचार करने की आवश्यकता समाप्त हो जाती है। / , क्योंकि हमेशा t The 2. इष्टतम स्थिति में संबंधित मान t ₀ द्वारा निरूपित किया जाएगा:

t ₀ ( A ₁ , A ₂ ) = मिनट ( d ₀ /) ₁ , डी ₀ / _२ )।

अंत में, हम नोट करते हैं कि सांख्यिकीय तालिकाओं में, और यह भी कि यह भ्रम की स्थिति नहीं है, हम तर्क ₁ और ए ₂ को छोड़ देंगे और बस लिखेंगे , डी ₀ , टी , टी ₀ , एन ।

2.2। सामान्य विशेषताएं

विचाराधीन रूसी वर्णमाला के प्रतीकों की 1770 छवियों में से, कुछ एक ही नाम के हैं (उदाहरण के लिए, अक्षर " सी ")। यह स्पष्ट है कि ऐसी जोड़ियों के लिए कई विशेषताएं "विपरीत" जोड़े की संगत विशेषताओं से बहुत भिन्न हो सकती हैं। इसलिए, कभी-कभी हम ऐसी जोड़ियों के आंकड़ों पर अलग से विचार करेंगे।

उन मामलों में जब कुल्हाड़ियों में से कुछ के साथ जोड़े की संख्या प्लॉट की जाती है, तो अधिकतम मूल्य बड़े हो सकते हैं, लेकिन छोटे मूल्यों को देखना हमारे लिए महत्वपूर्ण है। ऐसे मामलों में, हम लघुगणकीय पैमाने का उपयोग करेंगे: n → लॉग ₂ ( एन +1)।

आइए आंकड़ों को देखें। सबसे पहले, हम टी ₀ और टी के विभिन्न मूल्यों पर जोड़े की संख्या का सामान्य वितरण दिखाते हैं। चित्र 3 सभी जोड़े प्रतीकों के लिए निर्भरता n ( t ₀ ) और n ( t ) का एक हिस्टोग्राम दिखाता है।

क)

ख)

चित्र 3 - जोड़े की कुल संख्या a) t ₀ , b) t पर निर्भर करती है

हम कहते हैं कि सभी जोड़ियों के लिए t ₀ का औसत मान 0.6 है, t का औसत मान 0.66 है।

आइए हम चित्र 4 में एक ही नाम के जोड़े के लिए एक समान हिस्टोग्राम पर विचार करें।

क)

ख)

चित्रा 4 - एक ही नाम के प्रतीकों की संख्या की संख्या a) t ₀ , b) t पर निर्भर करती है

यहाँ, सभी जोड़ियों के लिए t ₀ का औसत मान 0.17 है, t का औसत मान 0.23 है।

औसतन, AL ₁ एल्गोरिथ्म उन मूल्यों को देता है जो इष्टतम से बहुत दूर नहीं हैं। उसी नाम के जोड़े के लिए, ग्राफ के दाईं ओर, n ( t ) के मान n ( t ₀ ) की तुलना में बहुत कम गिरते हैं। इसका मतलब यह है कि टी के बड़े मूल्य हमेशा संकेत नहीं देते हैं कि टी ₀ का संगत इष्टतम मूल्य बड़ा है। हालांकि, टी ₀ और टी के छोटे मूल्यों के लिए , दोनों रेखांकन लगभग समान हैं।

ध्यान दें कि, प्रमेय 5 को लागू करने के दृष्टिकोण से, और बड़े टी ₀ (उदाहरण के लिए, टी ₀ > 0.5) के साथ जोड़े को पहचानने के संदर्भ में, हम थोड़े से रुचि रखते हैं, इसलिए, उनके लिए एएल ₁ की गुणवत्ता और इष्टतम पारी की खोज बहुत महत्वपूर्ण नहीं है। ।

इसके अतिरिक्त, हम अंजीर में विचार करते हैं । 5 ₀ / t के मूल्य के आधार पर जोड़े की संख्या का एक हिस्टोग्राम।

चित्र 5 - निर्भरता n ( t ₀ / t )

जैसा कि हम देखते हैं, 15% से अधिक सभी जोड़े जोड़े को प्राप्त करते हैं, एएल ₁ एल्गोरिथ्म का उपयोग करते हुए, एक मूल्य जो सबसे अच्छा (आदर्श) मूल्य से 1% से अधिक नहीं होता है, और फिर टी ₀ / टी के साथ-साथ उनकी संख्या नीरस रूप से घट जाती है ।

इस प्रकार, हम मान सकते हैं कि इष्टतम स्थिति ( AL ₀ एल्गोरिथ्म) के साथ AL ₁ एल्गोरिथ्म द्वारा निर्धारित स्थिति की तुलना करके प्राप्त शिफ्ट आँकड़े काफी प्रतिनिधि होंगे।

2.3। आदर्श से प्रारंभिक स्थिति के विचलन का विश्लेषण

आइए अधिक विस्तार से टी के आधार पर आदर्श स्थिति से विचलन पर विचार करें। चित्र 6 में t की क्रिया के रूप में i = 0, 1, 2, 3, 4 और i > 4 द्वारा आदर्श स्थिति से शून्य स्थिति में जोड़े की संख्या n _i विचलन है ।

चित्र 6 - i पिक्सेल द्वारा आदर्श स्थिति से विचलन करने वाले जोड़े n _i ( t ) की संख्या, t के एक समारोह के रूप में ( n ₅ ( t ) - i > 4 के लिए जोड़े की संख्या)

यह ग्राफ से देखा जा सकता है कि t <0.13 के लिए सभी वर्णों के जोड़े पूरी तरह से स्थित हैं, लेकिन पहले से ही t > 0.22 जोड़े में 1 पिक्सेल के बदलाव की आवश्यकता वाले जोड़ों की संख्या आदर्श रूप से रखे गए लोगों की संख्या से अधिक है। और केवल t > 0.3 डू जोड़े में दिखाई देते हैं जिसमें 2 पिक्सेल की शिफ्ट की आवश्यकता होती है।

पिक्सेल विचलन / टी	0	1	2	3
0,0 - 0,12	4344	0	0	0
0.12 - 0.31	32,158	34,271	0	0
0.31 - 0.38	42	8809	38	0
0.38 - 0.49	0	3328	522	0
0.49 - 0.66	0	241	463	0
0.66 - 0.85	0	0	31	7

तालिका 1 - आदर्श से प्रारंभिक स्थिति के विभिन्न विचलन के साथ एक ही जोड़े की मात्रा का वितरण

हम ध्यान दें कि हालांकि प्रारंभिक स्थिति का निर्धारण करने के लिए एल्गोरिथ्म, जैसा कि पहले ही उल्लेख किया गया है, खराब नहीं है, टी पर निर्भरता यहां महत्वपूर्ण है, जैसा कि तालिका 1 से पता चलता है।

यह उन जोड़ों की संख्या देता है जिनमें आदर्श से प्रारंभिक स्थिति का विचलन i = 0, 1, 2 और i > 2 एक ही नाम के प्रतीकों के लिए है। हम देखते हैं कि यहां भी कुछ मामले ऐसे हैं जहां प्रारंभिक स्थिति आदर्श से बहुत दूर है, लेकिन ये सभी टी के पर्याप्त रूप से बड़े मूल्यों से संबंधित हैं।

अब तक, हमने आदर्श के साथ तुलना के लिए विशिष्ट एल्गोरिथ्म एएल _{1 का} उपयोग किया है। अब हम इस बात पर विचार करेंगे कि "शुद्ध रूप में" का सिद्धांत हमारे प्रयोग में कैसे काम करता है। अर्थात्, हम सभी दिशाओं में आदर्श स्थिति के सापेक्ष प्रत्येक जोड़े को पहले 1 पिक्सेल, फिर 2, 3 और 4 से आगे बढ़ाते हैं, और प्रत्येक मामले में हम सभी दिशाओं में न्यूनतम विचलन मानते हैं। इसलिए हम देखेंगे कि न्यूनतम मूल्य क्या है / जब आदर्श से भटक रहा हो | ए | (सभी 1565565 वर्णों के उपलब्ध जोड़े के लिए ( a = = 1, 2, 3 या चार से अधिक पिक्सेल)। इसके अलावा, प्रत्येक के लिए | ए | हम सूत्र (3) द्वारा एस _वी के न्यूनतम मूल्य की गणना करते हैं।

कब | और | = 1 के लिए t ₀ > 0.12 हमेशा एक ऐसी जोड़ी होती है जिसके लिए किसी भी दिशा में एक पिक्सेल की शिफ्ट t का मान नहीं बदलती है । अजीब तरह से, अन्य मूल्यों के लिए | ए | ऐसे उदाहरण भी पाए जाते हैं, लेकिन केवल टी ₀ > 0.5 पर, जो सैद्धांतिक अनुमानों की सीमा से परे हैं (कोरोल 3 की धारणा को याद करते हैं: << )। प्रयोगात्मक परिणाम तालिका 2 में दिखाए गए हैं।

| ए |	मिनट /	मिन एस वी
1	0.12	2.32
2	0.28	5.81
3	0.44	8.94
4	0.51	11.18

तालिका 2 - 1 / α और S _v का न्यूनतम मान जब 1, 2, 3, 4 या अधिक पिक्सेल से इष्टतम स्थिति से भटक रहा हो

तालिका 2 के आंकड़े आधारित सैद्धांतिक निष्कर्ष का अच्छी तरह से समर्थन करते हैं। टी <0.28 का मूल्य प्राप्त करने के बाद, यह आत्मविश्वास से कहा जा सकता है कि इष्टतम स्थिति दो पिक्सेल से अधिक नहीं है। और यहां तक ​​कि t = 0.43 (प्रतीक के लगभग आधे क्षेत्र के बराबर दूरी) पर, सापेक्ष स्थिति आदर्श स्थिति से तीन पिक्सेल से अधिक नहीं होती है।

इसी समय, यह स्पष्ट है कि सैद्धांतिक अनुमान | ए | < एस _वी कमजोर है। S _v का मूल्य हर जगह कई बार इष्टतम स्थिति से वास्तविक बदलाव से अधिक होता है

निष्कर्ष

हमने निकटता के माप के रूप में लेते हुए, द्विआधारी बिटमैप की तुलना में देखा - उनके बीच हैमिंग की दूरी। यह सिद्ध हो चुका है कि यदि काफी छोटा है, तो एक वस्तु के समानांतर स्थानांतरण = ( एच, वी ), मूल्य को कम करता है यह भी बड़ा नहीं हो सकता है। एक रचनात्मक अनुमान S _{v के लिए} प्राप्त किया जाता है | ए |

प्रतीकों की छवियों के साथ विचार किए गए प्रयोग में, सैद्धांतिक परिणाम पूरी तरह से पुष्टि किए जाते हैं। हालांकि, संभावित बदलाव की सीमाओं के सैद्धांतिक मूल्य Sv को वास्तविक पारियों के संबंध में कुछ हद तक कम आंका गया है, जो बहुत सामान्य सैद्धांतिक परिसर और अनुमानों की खुरदरापन को देखते हुए आश्चर्य की बात नहीं है।

लेख का पूरा पाठ Arlazarov V.L., Slavin O.A., Farsobina V.V, Khovansky A.G में प्रकाशित किया गया था। प्रतीकों की डिजीटल छवियों की तुलना करते हुए एक इष्टतम स्थिति की खोज करें। कृत्रिम बुद्धिमत्ता और निर्णय लेना, T.3। एम।: पॉलिप्रिंट सर्विस, 2013. एस। 48-59 "

साहित्य

1. ज़ुरावलेव यू।, रियाज़ानोव वी.वी., सेनको ओ वी। "मान्यता।" गणितीय तरीके। सॉफ्टवेयर प्रणाली। व्यावहारिक अनुप्रयोग। - एम।: फ़ाज़िस, 2005 ।-- एस 176। आईएसबीएन 5-7036-0108-8।
2. अर्लाजरोव वी। एल।, कोटोविच एन.वी., स्लाविन ओ.ए. अनुकूली मान्यता // सूचना प्रौद्योगिकी और कम्प्यूटिंग सिस्टम। - 2002, नंबर 4. - एस। 11-22। ISSN: 2071-8632।
3. अर्लाजारोव वी.एल., स्लाविन ओ.ए., खोवांसकी ए.जी. समानांतर हस्तांतरण के दौरान छवियों के बीच की दूरी का अनुमान // विज्ञान अकादमी के डॉकलाडी। - 2011, टी। 437, नंबर 3. - एस 313-315। ISSN: 0869-5652